5.NF.2. Word Problems
Keith picked 2 {5}/{6} buckets of apples and Sandy picked 4{1}/{3} buckets. How many money buckets of apples did sandy pick?
Jayson has 2{1}/{2} months' worth of pay saved in his account. He has 1{1}/{4} months' worth of pay saved in cash. Altogether, how much money has Jayson saved?

Answers
(a) Sandy picked \(1\frac{1}{2}\) more buckets than Keith .
(b) Jason have saved money for total of \(3\frac{3}{4}\) months .
In the question ,,
Part(a) ,
it is given that
number of buckets of apples Keith picked is = \(2\frac{5}{6}\) buckets ,
number of buckets of apples Sandy picked is = \(4\frac{1}{3}\) buckets
number of more buckets picked by Sandy is = (buckets picked by Sandy) - (buckets picked by Keith) .
= \(4\frac{1}{3}\) - \(2\frac{5}{6}\)
= 13/3 - 17/6 = 3/2 = \(1\frac{1}{2}\) buckets .
Part(b)
number of months that Jason saved money in account = \(2\frac{1}{2}\) months
number of months that Jason saved money in cash = \(1\frac{1}{4}\) months
total number of months for which money is saved is = \(2\frac{1}{2}\) + \(1\frac{1}{4}\)
Simplifying further ,
we get,
= 5/2 + 5/4
= 15/4
= \(3\frac{3}{4}\) months .
Therefore , (a) Sandy picked \(1\frac{1}{2}\) more buckets and (b) Jason saved money for \(3\frac{3}{4}\) months .
The given question is incomplete , the complete question is
(a) Keith picked \(2\frac{5}{6}\) buckets of apples and Sandy picked \(4\frac{1}{3}\) buckets. How many more buckets of apples did sandy pick ?
(b) Jayson has \(2\frac{1}{2}\) months worth of pay saved in his account. He has \(1\frac{1}{4}\) months worth of pay saved in cash. Altogether, how many months of money has Jayson saved ?
Learn more about Algebra here
https://brainly.com/question/11035479
#SPJ4
Related Questions
Two buildings are 18 m part. The shorter building is 12 m high while the taller one is 19 m high. Find the distance, x m between the top of the buildings.
Answers
The distance between the tops of the buildings is 28.5 meters.
To find the distance between the top of the buildings, we can use the concept of similar triangles.
Let's denote the height of the shorter building as "a" (12 m) and the height of the taller building as "b" (19 m). The distance between the buildings can be denoted as "c" (18 m), and the distance between the top of the buildings as "x" (which we need to find).
We can set up a proportion based on the similar triangles formed by the buildings:
a/c = b/x
Substituting the known values:
12/18 = 19/x
To find "x," we can cross-multiply and solve for "x":
12x = 18 * 19
12x = 342
x = 342/12
x = 28.5 m
Therefore, the distance between the tops of the buildings is 28.5 meters.
for such more question on distance
https://brainly.com/question/12356021
#SPJ8
Find the equation of the line through point (4,-7) and parallel to y =-2/3x + 3/2
Answers
Answer:
Hi
Step-by-step explanation:
Good bye. ;) (Stranger-Danger!) :)
2.
Find the products using
a. (5x - 2)(5x + 2)
Answers

the temperatures at midday on march 1st in five cities are shown in the bar chart below. What is the difference in temperature between rome and munich?
Answers
The difference in temperature between Rome and Munich is given as follows:
6ºC.
How to obtain the difference in temperatures?The difference in temperature between Rome and Munich is given by the subtraction of Rome's temperature by Munich's temperature.
The bar graph in the context of this problem gives the temperature for each town.
From the bar graph given by the image presented at the end of the answer, the temperatures for Rome and Munich are given as follows:
Rome: 11 ºC.Munich: 5 ºC.Hence the difference in temperature between Rome and Munich is given as follows:
11 - 5 = 6ºC.
Missing InformationThe graph is given by the image presented at the end of the answer.
More can be learned about difference of two amounts at https://brainly.com/question/17301989
#SPJ1

16) Michael is 4 feet tall. Explain how Michael could find his height in inches.
Then explain how he could find his height in yards.
Answers
By the process of conversion of unit, it can be found that
Height of Michael in inches is 48 inches
Height of Michael in yards is 1.33 yards
What is conversion of unit?
Conversion of unit is the process in which the value of one unit can be converted into the value of another unit.
Conversion of unit is very important especially in doing sums in physics or chemistry.
Here,
Michael is 4 ft tall
Now height of Michael in inches = \(12 \times 4\) inches
= 48 inches
Now, height of Michael in yards = \(4 \times \frac{1}{3}\) yards
= \(1.33\) yards
To learn more about conversion of unit, refer to the link:
https://brainly.com/question/141163
#SPJ13
When the sample mean lies relatively far away from µ0 in a hypothesis test, the decision should be to reject the null hypothesis.
When the sample mean lies relatively far away from µ0 in a hypothesis test, the decision should be to reject the null hypothesis.
True
False
Answers
The statement "When the sample means lies relatively far away from µ0 in a hypothesis test, the decision should be to reject the null hypothesis." is false
This is further explained below.
Whe do we reject the null hypothesis.?Generally, When the p-value is lower than or equal to your significance threshold, you should conclude that the null hypothesis is incorrect.
Your findings from the sample provide support to the alternative hypothesis, which indicates that the effect may be present in the population as a whole.
Remember, as a mnemonic device, that when the p-value is low, the null hypothesis must be discarded!
Read more about the null hypothesis.
https://brainly.com/question/19263925
#SPJ1
Can someone thats extremely good at math click on my name and go to my math questions and help me with them. Im failing math and need to bring my grade up. Please No Plagiarism. Will Mark Brainliest. Please dont answer if you dont know. Thank you. Need two responses.
Answers
Answer:
I'll be glad to assist you.
Step-by-step explanation:
f(x)=3x²-4x+2, what is f(-5), show work
Answers
Given f (x) = 3x^2 - 4x + 2; What is f (-5)
f (-5) = 3x^2 - 4x + 2
f (-5) = 3(-5)^2 - 4(-5) + 2
f (-5) = 3(25) - 4(-5) + 2
f (-5) = 75 + 20 + 2
f (-5) = 97
or
( -5 , 97 )
I need help I will list you as brainliest

Answers

The spray from a sprinkler reaches 21 feet from the sprinkler and creates a circle as it spins. What is the circumference of the circle sprayed by the sprinkler? Use 22/7 for π.
Answers
C=πd
r=21
d=42
C=132 ft, and D is your final answer. Hope it help!
Answer:
132
Step-by-step explanation:
D
Last question, and I have to go to soccer practice right now.

Answers
Answer:
7 hours.
Step-by-step explanation:
$6 x 7 = $48
$48 - $7= $41
Your teacher has 35 balloons. She buys 4 packs of balloons. Each pack has 10 balloons. How many does she have now?
Answers
Answer:
75
Step-by-step explanation:
35+4x where x is 10
35+4*10
35+40
75
Answer:
75
Step-by-step explanation:
4 packs of balloons which each have 10 balloons is 40 total balloons she bought. Add 40 to 35 which is 75.
PLEASE HELP!! What is the surface area of the cone?
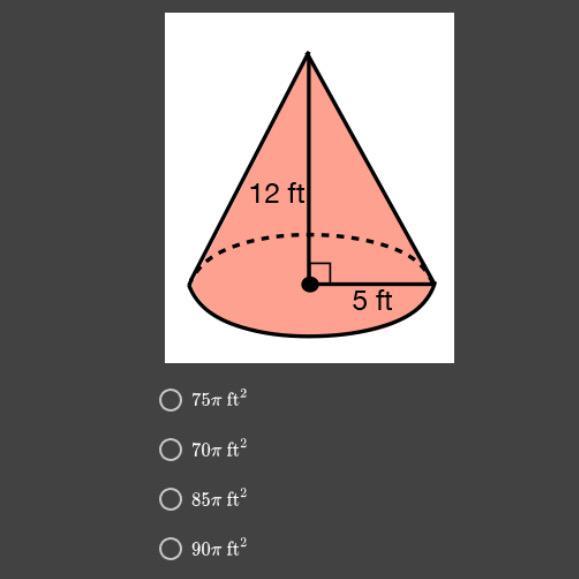
Answers
Hope this helped
The base of the mountain is 6,500 feet above sea level and AB measures 230 feet across. Given that the measurements for QAP is 20° and QBP is 35°, how far above sea level is peak P ? Express your answer to the nearest foot.
Height above sea level:

Answers
Answer:
6610
Step-by-step explanation:
We have tan(X) = opposite/ adjacent
tan(QBP) = PQ/BQ
tan(35) = PQ/BQ ---eq(1)
tan(QAP) = PQ/AQ
tan(20) = \(\frac{PQ}{AB +BQ}\)
\(=\frac{1}{\frac{AB+BQ}{PQ} } \\\\=\frac{1}{\frac{AB}{PQ} +\frac{BQ}{PQ} } \\\\= \frac{1}{\frac{230}{PQ} + tan(35)} \;\;\;(from\;eq(1))\\\\= \frac{1}{\frac{230 + PQ tan(35)}{PQ} } \\\\= \frac{PQ}{230+PQ tan(35)}\)
230*tan(20) + PQ*tan(20)*tan(35) = PQ
⇒ 230 tan(20) = PQ - PQ*tan(20)*tan(35)
⇒ 230 tan(20) = PQ[1 - tan(20)*tan(35)]
\(PQ = \frac{230 tan(20)}{1 - tan(20)tan(35)}\)
\(= \frac{230*0.36}{1 - 0.36*0.7}\\\\= \frac{82.8}{1-0.25} \\\\=\frac{82.8}{0.75} \\\\= 110.4\)
PQ = 110.4
≈110
Height above sea level = 6500 + PQ
6500 + 110
= 6610
Is this correct or not?
If not please provide correct answer

Answers
Answer:
It is correct please I do not want yo sound rude can you give me brainliest answer.
Answer:
correct steps
Step-by-step explanation:
if asked to find angles in terms of the ratios, then don't forget to shift sin / cos / tan across the equal sign and change it to arc sin / cos / tan.
Graph the function. f(x)=3sin(x)
Answers
Graphed f(x)=3sin(x) below in radians.

Kadeem has $50,000 in an account that compounds interest sem-annually at a rate of 1.8%. He withdraws $5,000 semiannually from the account
Will his money last:
4.5 years (yes or no), 5 years (yes or no), 5.5 years (yes or no), 6 years (yes or no)
Answers
The time taken is 5.3 years.
What is Compound Interest?Compound interest simply refers to the fact that an investment, loan, or bank account's interest accrues exponentially over time as opposed to linearly over time. The word "compound" is crucial here.
Compound interest is when you receive interest on both your interest income and your savings.
Given:
P = 50, 000
W= 5000
r= 1.8%= 0.018
n= 2
Using, P = W (1- \((1+ r/n)^{-nt}\)) / (r/n)
Putting all the values we get
P = W (1- \((1+ r/n)^{-nt}\)) / (r/n)
50000 = 5000 (1- \((1+0.018/2)^{-2t}\)) / (0.018/2)
10 = (1- \((1+0.009)^{-2t}\)) / (0.009)
0.09 = 1 - \((1.009)^{-2t\)
\((1.009)^{-2t\) = 0.91
Taking log on both side
-2t log 1.009 = log 0.91
t= log 0.91/ (log 0.091) / (-20
t= 5.3
Learn more about Compound Interest here:
https://brainly.com/question/14295570
#SPJ1
If a number is tripled and that result is decreased by 7, the result is the product of 2 and -8. What is the number?
Answers
Answer:
Step-by-step explanation:
Let the number be x .
Now ,
1 ) number is tripled : - 3x
2 ) result is decreased by 7 : - (3x - 7)
3 ) 3x - 7 = 2 x -8
3x - 7 = -16
3x = -9
x = -3
3(x+5)-2(-3x+1)
PLZ Answer
Answers
It should look like...
3x +15-6x-2
Then you would combine light terms.
And your final answer should be
-3x+13
PLEASE HELP!! ASAP NOWWWW Two races that a student runs every year are the 1492-mile race in his hometown and the -meter race in his college town. Complete parts (a) through (d) below.

Answers
Answer:
College town race is 31% of the home town race.
Step-by-step explanation:
Length of hometown race = 3 miles
Length of college town race = 1492 meters
Since 1 meter = 0.0006214 miles
Therefore, 1492 = 0.93 miles
Percentage of college town race to the hometown race,
= \(\frac{\text{College town race}}{\text{Home town race}}\times 100\)
= \(\frac{0.93}{3}\times 100\)
= 31%
Therefore, the college town race is 31% of the home town race.
Which describes the role of oxygen in photosynthesis?
It is a reactant, so it is released by the plant.
It is a product, so it is released by the plant.
It is a reactant, so it enters the plant.
It is a product, so it enters the plant,
Answers
Answer:
the answer is the first one.
Step-by-step explanation:
Answer:
b: It is a product, so it is released by the plant.
Step-by-step explanation:
good luck
AB and AD are tangent to circle C. Find the length of AB, if AB = 8x and AD = x + 9. Round your answer to 2 decimal places.
Answers
When a line is tangent to a circle, it forms a right angle with the radius drawn to the point of tangency. This means that triangle ABD is a right triangle with AB as the hypotenuse.
We can use the Pythagorean theorem to find the length of AB:
AB^2 = AD^2 + BD^2
Since AD = x + 9 and BD = 8x - (x + 9) = 8x - x - 9 = 7x - 9, we can substitute these values into the equation:
(8x)^2 = (x + 9)^2 + (7x - 9)^2
64x^2 = x^2 + 18x + 81 + 49x^2 - 126x + 81
64x^2 = 50x^2 - 108x + 162
14x^2 + 108x - 162 = 0
Dividing the equation by 2, we get:
7x^2 + 54x - 81 = 0
Using the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / (2a)
a = 7, b = 54, c = -81
x = (-54 ± √(54^2 - 4 * 7 * -81)) / (2 * 7)
x = (-54 ± √(2916 + 2268)) / 14
x = (-54 ± √5184) / 14
x = (-54 ± 72) / 14
Now we solve for x:
Case 1: x = (-54 + 72) / 14 = 18 / 14 = 9 / 7
Case 2: x = (-54 - 72) / 14 = -126 / 14 = -9
Since the length of a segment cannot be negative, we discard the second case and focus on the positive solution.
Therefore, x = 9/7.
Substituting this value back into AB = 8x:
AB = 8 * (9/7) = 72/7 ≈ 10.29
Rounding to 2 decimal places, the length of AB is approximately 10.29 units.
Answer:
To find the length of AB, we can use the property that two tangents to a circle from the same external point are equal. This means that AB = AD. Substituting the given values, we get:
8x = x + 9
Solving for x, we get:
x = 1.5
Therefore, AB = 8x = 8(1.5) = 12.
To check our answer, we can use the Pythagorean theorem on triangle ABD, since AB is perpendicular to BD at the point of tangency. We have:
AB^2 + BD^2 = AD^2
Substituting the values, we get:
12^2 + BD^2 = (1.5 + 9)^2
Simplifying, we get:
BD^2 = 56.25
Taking the square root of both sides, we get:
BD = 7.5
Hence, the length of AB is 12 and the length of BD is 7.5.
MARK AS BRAINLIEST!!!
Plssss help
According to a personal trainer's study, the equation yˆ=8.6067x+116.6567 models the average number of calories burned by a 160 lb individual, where x is amount of time spent weight lifting, in minutes, given the individual started the workout with a 10-minute jog.
According to this regression equation, what is the approximate calories burned for an individual who spent 30 minutes weight lifting?
Answers
Answer:
An individual who spent 30 minutes weight lifting will burn approximately 142.4768 calories.
Step-by-step explanation:
Given;
yˆ = 8.6067x + 116.6567 ............................... (1)
Where;
yˆ = The average number of calories burned by a 160 lb individual
x = Amount of time spent weight lifting
Since x is amount of time spent weight lifting, this implies that for an individual who spent 30 minutes weight lifting, x = 30
Substituting x = 30 into equation (1), we have:
yˆ = (8.6067 * 30) + 116.6567
yˆ = 25.8201 + 116.6567
yˆ = 142.4768
Therefore, an individual who spent 30 minutes weight lifting will burn approximately 142.4768 calories.
Cuál es el valor de la siguiente expresión?
(6 + 27) / (5 - 2)
Answers
Answer: 11
Step-by-step explanation:
6+27=33
33/3 = 11
If 2 cards are selected from a standard deck of 52 cards.The first card is placed back in the deck before the 2nd card is drawn.What is the probability that a heart and a club will be drawn ?
Answers
There are 13 cards of each suit.
Picking a heart would be 13/52 which reduces to 1/4
Then replacing the card and picking a club would be the same : 1/4
Picking a heart then a club would be 1/4 x 1/4 = 1/16
Answer: 1/16
In Mr. Stowe's math class, Katherine earned an 88 in the 1st quarter and a 94 in the end quarter. What is the percentage of increase?
Answers
The percentage of increase in her score is 6.82%
What is the percentage of increase?Here we will define her first score, 88, as the 100%.
So we can write the relation:
88 = 100%.
Her next score is 94, this will be a percentage X, then we can write:
94 = X
Taking the quotient between the two equations:
94/88 = X/100%
Solving this for X we get:
(94/88)*100% = X = 106.82%
The difference between the percentages gives the increase:
106.82% - 100% = 6.82%
Learn more about percentages:
https://brainly.com/question/843074
#SPJ1
I FORGOT IMAGE, please help me solve this!! 100 points!!

Answers
Answer:
\(\Large \boxed{\sf 384 \ m^2}\)
Step-by-step explanation:
Surface area ⇒ area of 2 triangles + area of 3 rectangles
\((8 \times 3 \times 0.5 \times 2)+(20 \times 5 \times 2+20 \times 8)=384\)
Answer:
Surface Area = 384 m²
Step-by-step explanation:
The given figure is a triangular prism.
The surface area of a triangular prism is made up of:
2 congruent triangles (the bases of the prism).3 rectangles.From inspection of the diagram, the dimensions of the triangular bases are:
Base = 8 mHeight = 3 m\(\boxed{\begin{aligned}\textsf{Area of a triangle}&=\dfrac{1}{2} \times \sf base \times height\\\\\implies \textsf{Area of triangular base}&=\dfrac{1}{2} \times 8 \times 3\\&=4 \times 3\\&=12\; \sf m^2 \end{aligned}}\)
From inspection of the diagram, there are two congruent rectangles with dimensions:
Length = 20 mWidth = 5 mand one rectangle with dimensions:
Length = 20 mWidth = 8 m\(\boxed{\begin{aligned}\textsf{Area of a rectangle}&=\sf width \times length\\\\\implies \textsf{Area of rectangle 1}&=5 \times 20\\&=100\; \sf m^2 \\\\\implies \textsf{Area of rectangle 2}&=8 \times 20\\&=160\; \sf m^2\end{aligned}}\)
Therefore, the total surface area of the given triangular prism is:
\(\begin{aligned}\textsf{Total Surface Area}&=\sf 2\;Triangles + 2\;Rectangle\;1+Rectangle\;2\\& = 2 \times 12+ 2 \times100+160\\& = 24+200+160\\& = 224+160\\& = 384\; \sf m^2\\\end{aligned}\)
Find the inverse of each function
1. f(x) = 4/(x+2) - 2
2. f(x)= -2x^5 - 3
Answers
9514 1404 393
Answer:
1. f^-1(x) = 4/(x+2) -2
2. f^-1(x) = (-(x+3)/2)^(1/5)
Step-by-step explanation:
1. As with all "inverse function" problems, solve for y:
x = f(y)
x +2 = 4/(y +2) . . . . add 2
y +2 = 4/(x +2) . . . . . multiply by (y+2)/(x+2)
y = 4/(x+2) -2 . . . . . subtract 2
We see that this function is its own inverse. The attached graph shows it is symmetrical about the line y=x.
f^-1(x) = 4/(x+2) -2
__
2. x = f(y)
x +3 = -2y^5 . . . . add 3
-(x +3)/2 = y^5 . . . . . divide by 2
(-(x +3)/2)^(1/5) = y . . . . take the 5th root
f^-1(x) = (-(x +3)/2)^(1/5)
In typeset form, that is ...
\(\displaystyle f^{-1}(x)=\sqrt[5]{\frac{-(x+3)}{2}}\\\\\text{or}\\\\f^{-1}(x)=-\frac{1}{2}\sqrt[5]{16x +48}\)
This last version is with the denominator "rationalized" and the contents of the radical "simplified." It may be a preferred form.
_____
The graphs show the function and inverse are symmetrical about the line y=x, as they should be.


Write a cosine function for the graph.

Answers
The correct option A: y = -4 cos Ф/4, is the cosine function for the graph.
Define the term cosine function?The ratio between the angle's adjacent leg and the hypotenuse when it is regarded as a leg of a right triangle is a trigonometric function for an acute angle.
One of the three fundamental trigonometric functions, cosine is the complement of sine (co+sine) and one of the three main trigonometric functions.Y=cos(x) has its greatest value when x = 2nπ, wherein n is an integer. Y=cos(x) has a lowest value for x= π+2nπ , wherein n is an integer.For the given graph,
cosine function: y = -4 cos Ф/4.
In which, -4 is the amplitude (maximum displacement from the x axis).
Negative sign shows, the displacement is taken along negative y-axis.
And, Ф/4 is the phase angle.
Thus, the cosine function for the graph is y = -4 cos Ф/4.
To know more about the cosine function, here
https://brainly.com/question/27587720
#SPJ1
Answer:
b. \(\displaystyle y = -4cos\:4\theta\)
Step-by-step explanation:
\(\displaystyle y = 4cos\:(4\theta \pm \pi) \\ \\ \\ y = Acos(B\theta - C) + D \\ \\ Vertical\:Shift \hookrightarrow D \\ Horisontal\:[Phase]\:Shift \hookrightarrow \frac{C}{B} \\ Wavelength\:[Period] \hookrightarrow \frac{2}{B}\pi \\ Amplitude \hookrightarrow |A| \\ \\ Vertical\:Shift \hookrightarrow 0 \\ Horisontal\:[Phase]\:Shift \hookrightarrow \frac{C}{B} \hookrightarrow \boxed{\pm\frac{\pi}{4}} \hookrightarrow \frac{\pm\pi}{4} \\ Wavelength\:[Period] \hookrightarrow \frac{2}{B}\pi \hookrightarrow \boxed{\frac{\pi}{2}} \hookrightarrow \frac{2}{4}\pi \\ Amplitude \hookrightarrow 4\)
OR
\(\displaystyle y = -Acos(B\theta - C) + D \\ \\ Vertical\:Shift \hookrightarrow D \\ Horisontal\:[Phase]\:Shift \hookrightarrow \frac{C}{B} \\ Wavelength\:[Period] \hookrightarrow \frac{2}{B}\pi \\ Amplitude \hookrightarrow |A| \\ \\ Vertical\:Shift \hookrightarrow 0 \\ Horisontal\:[Phase]\:Shift \hookrightarrow 0 \\ Wavelength\:[Period] \hookrightarrow \frac{2}{B}\pi \hookrightarrow \boxed{\frac{\pi}{2}} \hookrightarrow \frac{2}{4}\pi \\ Amplitude \hookrightarrow 4\)
You will need the above information to help you interpret the graph. First off, keep in mind that this cosine graph will have TWO equations because the curvature begins upward from \(\displaystyle [0, -4]\) instead of downward from \(\displaystyle [0, 4],\) telling you that one equation will have a “negative” symbol inserted in the beginning of the equation. Before we go any further though, we must figure the period of the graph out. So, in this case, sinse you ONLY have a graph to wourk with, you MUST figure the period out by using wavelengths. So, looking at where the graph hits \(\displaystyle [0, -4],\)from there to \(\displaystyle [-\frac{\pi}{2}, -4],\) they are obviously \(\displaystyle \frac{\pi}{2}\:unit\)apart, telling you that the period of the graph is \(\displaystyle \frac{\pi}{2}.\) Now, as you can see, the photograph on the right displays the trigonometric graph of \(\displaystyle y = 4cos\:4\theta.\) Now, if you look hard enough, you will see that both graphs are “mirror reflections” of one another, meaning you can figure the rest of the terms out one of two ways. The first way is to figure the appropriate C-term out that will make the graph horisontally shift and map onto the original cosine graph [photograph on the left], accourding to the horisontal shift formula above. Also, keep in mind that −C gives you the OPPOCITE TERMS OF WHAT THEY REALLY ARE, so you must be careful with your calculations. So, between the two photographs, we can tell that the rightward graph is shifted \(\displaystyle \frac{\pi}{4}\:unit\) on both sides of the y-axis, which means that in order to match the original graph, we need to shift the graph back, which means the C-term will be both negative and positive; and by perfourming your calculations, you will arrive at \(\displaystyle \boxed{\pm\frac{\pi}{4}} = \frac{\pm\pi}{4}.\)So, one equation of the cosine graph, accourding to the horisontal shift, is \(\displaystyle y = 4cos\:(4\theta \pm \pi).\) Now that we got this out the way, we can focuss on finding the second equation. Another way is to write an equation with a “negative” symbol inserted in the beginning [like I mentioned earlier]. Now, sinse we are writing an equation with the negative, the graph will not have a horisontal shift; so, C will be zero. With this said, the second equation is \(\displaystyle y = -4cos\:4\theta.\) Now, the amplitude is obvious to figure out because it is the A-term, but of cource, if you want to be certain it is the amplitude, look at the graph to see how low and high each crest extends beyond the midline. The midline is the centre of your graph, also known as the vertical shift, which in this case the centre is at \(\displaystyle y = 0,\) in which each crest is extended four units beyond the midline, hence, your amplitude. So, no matter how far the graph shifts vertically, the midline will ALWAYS follow.
I am delighted to assist you at any time.


How many solutions does y - 13 =5x
Y - 5x =12
Show all work
A no solution
B one solution
C infinity solutions
Answers
9514 1404 393
Answer:
no solutions
Step-by-step explanation:
Subtract the second equation from the first:
(y -13) -(y -5x) = (5x) -(12)
5x -13 = 5x -12 . . . . . . simplify
0 = 1 . . . . . . . . . . . . . . .add 13-5x to both sides
No value of the variable will make this statement true.
There is no solution.