598,500 round to the nearest ten thousand
Answers
598,500 round to the nearest ten thousand is 600000.
What is rounding of numbers ?We round nos. to make our calculation or remembering easier to get an estimated result.
According to the given question
We have to round 598500 to the nearest ten thousand.
To round 598500 to nearest ten thousand first we'll look at the digit at thousand's place in this case it 8 so in this case we'll add 1 to the digit and put 0's after it.
∴ 8500 becomes 9000
Now the number 599000 we'll look at the digit at ten thousand's place which is 9 we'll add 1 to it which will make it 0 and 1 will carry and we'll put 0's after it.
∴ 599000 will become 600000 rounded to ten thousand's place.
learn more about rounding of nos. here :
https://brainly.com/question/19031319
#SPJ2
Related Questions
what is the soultion for y=1/2x-4 and y = 1/2x+5
Answers
In the system:
\(\begin{gathered} y=\frac{1}{2}x-4 \\ y=\frac{1}{2}x+5 \end{gathered}\)Both lines have the same slope, this means that they are parallel. The solution for a system of equations is the point were these two lines meet. But when 2 lines are parallel, they don't meet (never). This means that this system has no solution.
how do i solve this Please give me a advise

Answers
The probability of spinning an even number, flipping tails, then spinning an odd number is:
1/9 (as fraction) or 11.11% (as percent)
How to find the probability of spinning an even number, flipping tails, then spinning an odd number?
To find the probability of spinning an even number, flipping tails, then spinning an odd number. We need to consider the individual probabilities. That is:
We have only one even number in the spinner, and that is 2. Thus,
P(even number) = 1/3
For a coin, the probability of head or tail is 1/2. Thus,
P(tail) = 1/2
We have two odd number in the spinner, and that is 1 and 3. Thus,
P(odd number) = 2/3
Therefore, the probability of spinning an even number, flipping tails, then spinning an odd number will be:
P(even, tail, odd) = 1/3 * 1/2 * 2/3
= 2/18
= 1/9 (as fraction)
In percent:
P(even, tail, odd) = 1/9 * 100
= 11.11%
Learn more about probability on:
https://brainly.com/question/24756209
#SPJ1
Irinkers or both? Acme electronics manufactures MP3 players at three locations. The plant 50% of the MP3 players and 1% are defective. The plant at Memphis manu that plant are defective. The plant at Fort Meyers manufactures 20% and 3% If an MP3 player is selected at random, what is the probability that it is defe Refer to Problem 6.101. An MP3 player is found to be defective. What is th manufactured in Fort Meyers?
Answers
The probability that an MP3 player manufactured in Fort Meyers is defective is 0.37%.
To calculate the probability that an MP3 player is defective, we need to consider the manufacturing plants and their respective defect rates.
Given:
Plant at Memphis manufactures 50% of the MP3 players, and 1% of those manufactured at that plant are defective.
Plant at Fort Meyers manufactures 20% of the MP3 players, and 3% of those manufactured at that plant are defective.
No information is provided about the defect rate of the third plant.
To find the overall probability of an MP3 player being defective, we need to consider the probability of selecting a defective player from each plant and then weigh it by the probability of selecting a player from each plant.
Let's calculate the overall probability:
Probability of selecting a defective player from Memphis plant = 50% * 1% = 0.50% or 0.005 (since 50% is equivalent to 0.50 in decimal form)
Probability of selecting a defective player from Fort Meyers plant = 20% * 3% = 0.60% or 0.006 (since 20% is equivalent to 0.20 in decimal form)
To calculate the overall probability, we need to weigh these probabilities by the probability of selecting an MP3 player from each plant:
Probability of selecting from Memphis plant = 50% = 0.50 (decimal form)
Probability of selecting from Fort Meyers plant = 20% = 0.20 (decimal form)
Overall probability of selecting a defective MP3 player is given by:
Overall probability = (Probability from Memphis plant * Probability of selecting a defective player from Memphis) + (Probability from Fort Meyers plant * Probability of selecting a defective player from Fort Meyers)
Overall probability = (0.50 * 0.005) + (0.20 * 0.006) = 0.0025 + 0.0012 = 0.0037 or 0.37%
Therefore, the probability that an MP3 player, manufactured in Fort Meyers, is defective is 0.37%.
For more question on probability visit:
https://brainly.com/question/25839839
#SPJ8
Find the values of x and y.
y
45

Answers
Answer:
x = \(\sqrt{2}\)
y = 2
Step-by-step explanation:
By applying tangent rule in the given triangle,
tan(45°) = \(\frac{\text{Opposite side}}{\text{Adjacent side}}\)
1 = \(\frac{\sqrt{2}}{x}\)
x = √2
By applying sine rule in the given triangle,
sin(45°) = \(\frac{\text{Opposite side}}{\text{Hyotenuse}}\)
\(\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{y}\)
y = \((\sqrt{2})^2\)
y = 2
geometric series $b 1 b 2 b 3 \cdots b {10}$ has a sum of $180$. assuming that the common ratio of that series is $\dfrac{7}{4}$, find the sum of the series $b 2 b 4 b 6 b 8 b {10}.$
Answers
The sum of the series b 2 b 4 b 6 b 8 b {10} is \($\dfrac{180}{3}$\) since it is a geometric series with a common ratio of \($\dfrac{7}{4}$\).
Since the given series \($b 1 b 2 b 3 \cdots b {10}$\) has a sum of 180, it can be deduced that the series is a geometric series with a common ratio of\($\dfrac{7}{4}$\). This means that the ratio of any two consecutive terms in the series is a constant, \($\dfrac{7}{4}$\). Therefore, the sum of the series b 2 b 4 b 6 b 8 b {10} can be calculated as follows:
\($S = b2 + b4 + b6 + b8 + b_{10}$\)
\($= b2\left(\dfrac{7}{4}\right)^0 + b2\left(\dfrac{7}{4}\right)^2 + b2\left(\dfrac{7}{4}\right)^4 + b2\left(\dfrac{7}{4}\right)^6 + b2\left(\dfrac{7}{4}\right)^8$\)
\($= b2 \left[1 + \left(\dfrac{7}{4}\right)^2 + \left(\dfrac{7}{4}\right)^4 + \left(\dfrac{7}{4}\right)^6 + \left(\dfrac{7}{4}\right)^8\right]$\)
\($= b2 \left[\dfrac{1-\left(\dfrac{7}{4}\right)^{10}}{1-\left(\dfrac{7}{4}\right)^2}\right]$\)
\($= b2 \left[\dfrac{1-\left(\dfrac{7}{4}\right)^{10}}{\dfrac{3}{4}}\right]$\)
\($= \dfrac{4b2}{3} \left[1-\left(\dfrac{7}{4}\right)^{10}\right]$\)
Since the sum of the series\($b 1 b 2 b 3 \cdots b {10}$\) is 180, we can substitute $b2$ with \($\dfrac{180}{3}$\)nd calculate the sum of the series $b 2 b 4 b 6 b 8 b {10}$:
\($S = \dfrac{4\left(\dfrac{180}{3}\right)}{3} \left[1-\left(\dfrac{7}{4}\right)^{10}\right]$\)
\($= \dfrac{180}{3} \left[1-\left(\dfrac{7}{4}\right)^{10}\right]$\)
Therefore, the sum of the series \($b 2 b 4 b 6 b 8 b {10}$ is $\dfrac{180}{3}$\).
Learn more about ratio here
https://brainly.com/question/13419413
#SPJ4
what is the volume of the cylinder below height 15 radius 11
Answers
Answer:
πr^2 h
π(11)^2 (15)
= 1815π or = 5701
WILL MARK BRAINLIEST!!!
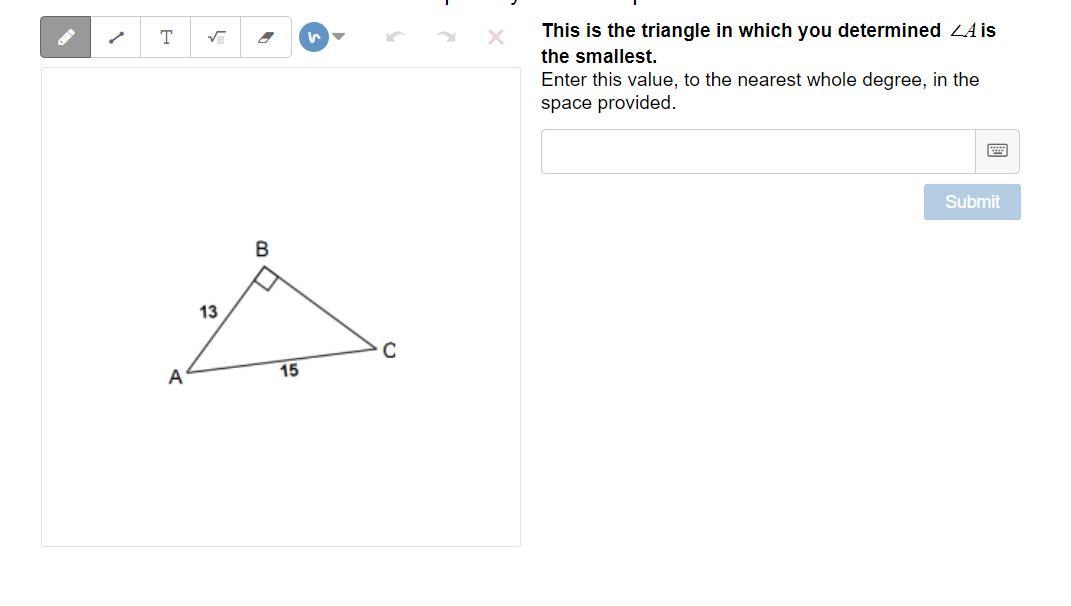
Q1= This is the triangle in which you determined `∠A`is the smallest.
Enter this value, to the nearest whole degree, in the space provided.
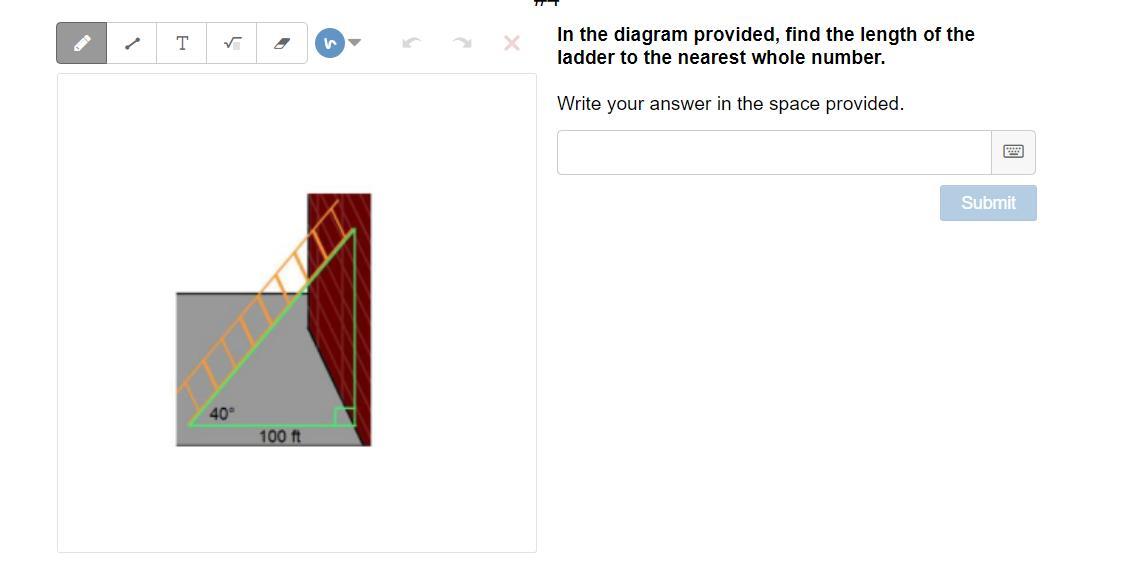
Q2=In the diagram provided, find the length of the ladder to the nearest whole number.
Write your answer in the space provided
Answers
Q1) The angle A in the given triangle is: 29.93°
Q2) The length of the ladder to the nearest whole number is: 131 ft
How to use Pythagoras Theorem?Pythagoras Theorem is defined as the way in which you can find the missing length of a right angled triangle.
The triangle has three sides, the hypotenuse (which is always the longest), Opposite (which doesn't touch the hypotenuse) and the adjacent (which is between the opposite and the hypotenuse).
Pythagoras is in the form of; a² + b² = c²
Q1) Thus:
BC = √(15² - 13²)
BC = 7.4833
Thus:
7.4833/sin A = 15/sin 90
(7.4833 * sin 90)/15 = sin A
0.4989 = sin A
A = sin⁻¹0.4989
A = 29.93°
Q2) Using Trigonometric ratio, the height of the ladder is:
100/x = cos 40
x = 100/0.766
x = 131 ft
Read more about Pythagoras Theorem at: https://brainly.com/question/343682
#SPJ1
Obtain an estimate for the computation shown below by rounding the numbers so that the resulting arithmetic can easily be performed by hand or in your head.
0.87 x 310
Answers
The estimation of the numbers given as 0.87 × 310 will give 270.
Howw to calculate the estimation?You must approximate (eliminate or round off) the decimals to obtain whole numbers before you can use the whole numbers to find the product of two decimals using estimation.
A figure is discovered through estimation.
A value, amount, or size that rounds off to the nearest whole number is said to be approximating.
The estimation of the numbers given as 0.87 × 310 will give:
= 0.9 × 300
= 270.
Learn more about estimation on
https://brainly.com/question/28416295
#SPJ1
A customer wants rhombus-shaped tiles for his countertops. The height is 3 inches and the length of each side is 6.5 inches. What is the area of each tile?
Answers
Answer:
The length of each side of the tiles is 7.2 in
Step-by-step explanation:
Given:
Height of the tile, h = 3 in
Area of each tile, A = 21.6 in²
Length of each side, a = ?
We know:
A rhombus is a type of quadrilateral whose opposite sides are parallel and equal.Also, the opposite angles of a rhombus are equal and the diagonal intersect each other perpendicularly.
To find the area of a rhombus when the measures of its height and side length are given, use the formula
A = Base X height
21.6 in² = a X 3 in
a = 7.2 in
Therefore, the length of each side of the tiles is 7.2 in
Find the missing value

Answers
Answer:
the answer to this question is 19
Answer: m=19
Step-by-step explanation:
First you cross multiply the two fractions. So you get 9*m = 57*3.
When you put 57*3 in a calculator you get 171. So the equation is 9m=171 and then to isolate the x you divide by 9. So when you put 171/9 in a calculator you get 19. So the correct answer is C. 19.
2. Joanne's car insurance is reduced by 10% for each year that she has not had an
accident.
The normal cost of her insurance is £420 but she has a 3-years' no claims bonus.
How much is her insurance?
Answers
Answer:
220
Step-by-step explanation:
Solve for x |x| = 4
Answers
Answer:
x = 2
Step-by-step explanation:
You want the value of x that satisfies x|x| = 4.
DomainThe absolute value function splits the domain of the equation into two parts.
For x < 0, the equation is ...
x(-x) = 4
x² = -4
There are no real solutions in this domain.
For x ≥ 0, the equation is ...
x² = 4
x = √4 = 2
The only solution is x = 2.
__
Additional comment
In the attachment, we have rewritten the equation to ...
x|x| -4 = 0
The graphing calculator readily identifies x-intercepts, so this is a convenient way to find the solution. You will notice that for x < 0, the graph is of -x²-4, which is never zero.
<95141404393>

order from least to greatest )
-3/4, 0, 3, 0.75, 1.8, 3.5
tysm <3
Answers
Answer:
-3/4 = -0.75
-0.75, 0, 0.75, 1.8, 3, 3.5
Hope this helps!
Rajan ran 15km in 90 mins. How hast did he run.
Answers
2700 bc in everminutes he would run 920
Answer:
6
Step-by-step explanation:
Hi can someone help me out. This is due by the end of the day.

Answers
Answer:
It's called the diameter of the circle
In the context of this problem, which solutions to the polynomial equation can you eliminate because they do not make sense? x = –8 x = –4 x = 6
Answers
In the context of this problem all the solutions to the polynomial equation is correct because they all make sense.
What is the solution to the equation?The given polynomial equation can be expressed as ;
x³ + 6x² - 40x = 192 and the given solutions can be written as ; x = -8, x = -4, and x = 6
We can test if the solution is the best for the given euation because this will help us to know if these valueas are the solution for the equation
x = -8
[(-8)³ + 6(-8)² - 40(-8)]
= 192
[-512 + 384 + 320]
= 192
x = -4,
[(-4)³ + 6(-4)² - 40(-4)]
[-64 + 96 + 160 ]
= 192
x = 6
[(6)³ + 6(6)² - 40(6) ]
216 + 216 - 240
= 192
Learn more about polynomial equation at:
https://brainly.com/question/19837586
#SPJ1
Answer:
Step-by-step explanation:
A,B
x = –8
x = –4
Choose the best definition for the following term: variable
Answers
Step-by-step explanation:
a variable is a quantity that may change within the context of a mathematical problem or experiment
I hope this was helpful
FOR BRAINLSIT!!!
A
B
C
D

Answers
Answer:
The 2nd option is correct
Step-by-step explanation:
The only numbers on a dice greater than 4 are 5 and 6, and we want to get the color blue, so the 2nd option is correct.
Answer:
Imma have to say B but I'm not sure
34 + (-21) +15 = 0
5
-2
NE
2.
Answers
Answer:
\(34 + ( - 21) + 15 = 28\)
Simplify 3(x+2) + 2x + 5
Answers
Answer:
\(5x+11\)
Step-by-step explanation:
Step 1: Distribute
\(3x+6+2x+5\)
Step 2: Add like terms
\(5x+11\) < your answer
Which is the graph of the function f/x )= x 2 2x 3?; Which graph represents the function f/x )= 4 x?; How do you find a function on a graph?; Which is one of the transformations applied to the graph of f/x )= x2 to change it into the graph?
Answers
The graph of the function f(x) = x² + 2x + 3 is a parabola with vertex (-1, 2).
You can use the vertical line test on a graph to determine whether a relation is a function. If it is impossible to draw a vertical line that intersects the graph more than once, then each x-value is paired with exactly one y-value. So, the relation is a function.
Given, the function is f(x) = x² + 2x + 3
We have to find the graph of the function.
Let y = x² + 2x + 3
Put x = -3
y = (-3)² + 2(-3) + 3
= 9 - 6 + 3
= 9 - 3
y = 6
Put x = -2
y = (-2)² + 2(-2) + 3
= 4 - 4 + 3
y = 3
Put x = -1
y = (-1)² + 2(-1) + 3
= 1 - 2 + 3
= 4 - 2
y = 2
Put x = 0
y = (0)² + 2(0) + 3
= 0 + 0 + 3
y = 3
Put x = 1
y = (1)² + 2(1) + 3
= 1 + 2 + 3
= 3 + 3
y = 6
We can plot the graph using the points.
The graph of the function f(x) = x² + 2x + 3 is a parabola with vertex (-1, 2).
Learn more about graph of quadratic equation at :
https://brainly.com/question/16191913
#SPJ4

A walk-in medical clinic believes that arrivals are uniformly distributed over weekdays (Monday through Friday). It has collected the following data based on a random sample of 100 days. Frequency Mon 25 Tue 22 Wed 19 Thu 18 Fri 16 Total 100 Assuming that a goodness-of-fit test is to be conducted using a 0.10 level of significance, the critical value is:
Answers
Answer:
The degrees of freedom are given by;
\( df =n-1= 5-1=4\)
The significance level is 0.1 so then the critical value would be given by:
\( F_{cric}= 7.779\)
If the calculated value is higher than this value we can reject the null hypothesis that the arrivals are uniformly distributed over weekdays
Step-by-step explanation:
For this case we have the following observed values:
Mon 25 Tue 22 Wed 19 Thu 18 Fri 16 Total 100
For this case the expected values for each day are assumed:
\( E_i = \frac{100}{5}= 20\)
The statsitic would be given by:
\( \chi^2 = \sum_{i=1}^n \frac{(O_i-E_i)^2}{E_i}\)
Where O represent the observed values and E the expected values
The degrees of freedom are given by;
\( df =n-1= 5-1=4\)
The significance level is 0.1 so then the critical value would be given by:
\( F_{cric}= 7.779\)
If the calculated value is higher than this value we can reject the null hypothesis that the arrivals are uniformly distributed over weekdays
The ratio of boys to girls in Mrs. Ronilo's class is 3 to 1. What PERCENT of the class is girls.
A. 25%
B.33%
C.66%
D.75%
PLS HURRY I AM IN THE MIDDLE OF THIS TEST.
Answers
I hope this helps
Easy math help picture below problem 4

Answers
Answer: is 126 degrees
Step-by-step explanation:
Calculate the volume, in cubic centimeters, of a box which is 125 cm long, 37 cm wide, and 68 cm high. Report your answer with correct significant figures in cubic centimeters.
Answers
Answer:
\(Volume = 314500cm^3\)
Step-by-step explanation:
Given
\(Length = 125cm\)
\(Width = 37cm\)
\(Height = 68cm\)
Required
Determine the volume
Volume is calculated as:
\(Volume = Length * Width * Height\)
Substitute values for Length, Width and Height
\(Volume = 125cm * 37cm * 68cm\)
\(Volume = 314500cm^3\)
Hence, the volume of the box is \(314500cm^3\)
Can someone help me please, ASAP!! Thank you!

Answers
Calculate the length of segment CD, given that AE is tangent to the circle, AE = 12, and EC = 8.
Answers
The length of segment CD is approximately 28.84.
To calculate the length of segment CD, we need to use the properties of a tangent line and the given information.
In a circle, when a line is tangent to the circle, it forms a right angle with the radius drawn to the point of tangency. This means that triangle AEC is a right triangle.
Given that AE = 12 and EC = 8, we can use the Pythagorean theorem to find the length of AC, which is the hypotenuse of triangle AEC.
AC^2 = AE^2 + EC^2
AC^2 = 12^2 + 8^2
AC^2 = 144 + 64
AC^2 = 208
Taking the square root of both sides:
AC = √208
AC ≈ 14.42
Now, segment CD is a part of the diameter of the circle and passes through the center of the circle. Therefore, it is twice the length of the radius.
CD = 2 * AC
CD = 2 * 14.42
CD ≈ 28.84
for similar questions on length of segment.
https://brainly.com/question/28322552
#SPJ8
Determine how many integer solutions there are to
x₁ + x₂ + x3 + x₁ = 20, if
0≤x₁ < 3, 0≤ x₂ < 4, 0≤x3 <5, 0≤x4 < 6
Answers
Based on the information given, there are a total of 118 solutions.
How many possible solutions are there?This is a problem of solving a Diophantine equation subject to some conditions. Let's introduce a new variable y4 = 20 - (x1 + x2 + x3 + x4). Then the problem can be restated as finding the number of solutions to:
x1 + x2 + x3 + y4 = 20
Subject to the following conditions:
0 ≤ x1 < 3
0 ≤ x2 < 4
0 ≤ x3 < 5
0 ≤ y4 < 6
We can solve this problem using the technique of generating functions. The generating function for each variable is:
(1 + x + x^2) for x1
(1 + x + x^2 + x^3) for x2
(1 + x + x^2 + x^3 + x^4) for x3
(1 + x + x^2 + x^3 + x^4 + x^5) for y4
The generating function for the equation is the product of the generating functions for each variable:
(1 + x + x^2)^3 (1 + x + x^2 + x^3 + x^4 + x^5)
We need to find the coefficient of x^20 in this generating function. We can use a computer algebra system or a spreadsheet program to expand the product and extract the coefficient. The result is: 1118
Learn more about solutions in https://brainly.com/question/30665317
#SPJ1
Answer: This problem involves finding the number of non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20 subject to the given constraints. We can use the stars and bars method to solve this problem.
Suppose we have 20 stars representing the sum x₁ + x₂ + x3 + x₁. To separate these stars into four groups corresponding to x₁, x₂, x₃, and x₄, we need to place three bars. For example, if we have 20 stars and 3 bars arranged as follows:
**|**||
then the corresponding values of x₁, x₂, x₃, and x₄ are 2, 4, 6, and 8, respectively. Notice that the position of the bars determines the values of x₁, x₂, x₃, and x₄.
In general, the number of ways to place k identical objects (stars) into n distinct groups (corresponding to x₁, x₂, ..., xₙ-₁) using n-1 separators (bars) is given by the binomial coefficient (k+n-1) choose (n-1), which is denoted by C(k+n-1, n-1).
Thus, the number of non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20 subject to the given constraints is:
C(20+4-1, 4-1) = C(23, 3) = 1771
However, this count includes solutions that violate the upper bounds on x₁, x₂, x₃, and x₄. To eliminate these solutions, we need to use the principle of inclusion-exclusion.
Let Aᵢ be the set of non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20 subject to the given constraints, where xᵢ ≥ mᵢ for some integer mᵢ. Then, we want to find the cardinality of the set:
A = A₀ ∩ A₁ ∩ A₂ ∩ A₃
where A₀ is the set of all non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20, and Aᵢ is the set of solutions that violate the upper bound on xᵢ.
To find the cardinality of A₀, we use the formula above and obtain:
C(20+4-1, 4-1) = 1771
To find the cardinality of Aᵢ, we subtract the number of solutions that violate the upper bound on xᵢ from the total count. For example, to find the cardinality of A₁, we subtract the number of solutions where x₂ ≥ 4 from the total count. To count the number of solutions where x₂ ≥ 4, we fix x₂ = 4 and then count the number of solutions to the equation x₁ + 4 + x₃ + x₄ = 20 subject to the constraints 0 ≤ x₁ < 3, 0 ≤ x₃ < 5, and 0 ≤ x₄ < 6. This count is given by:
C(20-4+3-1, 3-1) = C(18, 2) = 153
Similarly, we can find the cardinalities of A₂ and A₃ by fixing x₃ = 5 and x₄ = 6, respectively. Using the principle of inclusion-exclusion, we obtain:
|A| = |A₀| - |A
Step-by-step explanation:
9.2x8.9= please put shown work on it please and thank you if you do then i will mark you as the brainist
Answers
Answer:
81.88 is the answer
Step-by-step explanation:
There are 13 maple trees currently in the park. Park workers will plant more maple trees today. When the workers are finished, there will be 88 maple trees in the park. How many maple trees did the workers plant today