(5126789+123434425).5
Answers
Answer:
128561214
Step-by-step explanation:
Hope it helped you (5126789+123434425)=128561214
Related Questions
Determine the equation of the circle graphed below.

Answers
Answer:
(x-4)^2+(y-1)^2=9
Step-by-step explanation:
diameter = 6
radius = diameter/2 = 3
center (h,k) = (4,1)
standard equation of a circle (x-h)^2 + (y-k)^2=r^2
(x-4)^2+(y-1)^2=9
which of these correctly rearranges the terms in this polynomial so like terms are next to each other ? 3-6x+4x^2+3x-6x^2-4 PLEASE HELP!!

Answers
Answer:
A is the answer
Step-by-step explanation:
Answer:
the answer is A.
Step-by-step explanation:
Help me please i am marking brainiest, no one ever helps me with anything i am really struggling as a kid to move on to the next grade so please me me out with this problem please for i can force myself to keep going:
A student is doing a reading assignment. After 37 minutes of reading, she skims the pages ahead and estimates that she still has 55% of the reading to do. According to the girl's estimate, how long is the total reading assignment? Round to the nearest minute.
Answers
If you multiply this by 100% you get 122 minutes for the total assignment
what does 5+3x/2 equal?
Answers
i dont konw what the dash is so im going to do both, the one where its a fraction and just division. The first one will be as regular divison.
1- It will equal .25
2-it would equal 3.3
I have no idea which one you need or which one will help but hopefully one of these will be helpful.
Adrian, Ben and Charlie share some sweets in the ratio 7.4.11
Charlie got 52 more sweets than Adrian. Work out the total amount of sweets.
Answers
Answer:
286 sweets.
Step-by-step explanation:
If Adrian had x sweets, Charlie got x+52 sweets.
The number of parts is 7+4+11 = 22.
So Adrian had 7/22 of the total and Charlie had 11/22 = 1/2 of the total.
This means that Ben had 4/22 = 2/11 of the total.
If y is the total number of sweets:
y = x + x + 52 + 2y/11
9y/11 = 2x + 52
2x = 9y/11 - 52.............(1)
Also x + 52 = y/2
y = 2x + 104
2x = y - 104...............(2)
Equating (1) and (2) - (as there is 2x on left side of both equations):-
9y/11 - 52 = y - 104
52 = 2y/11
y = 52 * 11/2
y = 286 sweets.
Find EF in the trapezoid.

Answers
Answer:
it's 18. i just had the same questionand didn't get it right and the answer said it was 18
Step-by-step explanation:
Sixty-four percent of voters in a very large electorate support candidate Smith in an upcoming election. A student employee working the evening shift at a telephone survey facility calls voters at random and asks them which candidate they prefer. a. What is the probability that, among five voters the student calls, exactly one supports candidate Smith? b. What is the probability that, among five voters the student calls, at least one supports candidate Smith? c. What is the probability that the first voter supporting candidate Smith is reached on the fifth call, i.e., what is the probability that it takes the student five calls to reach the first voter who supports candidate Smith? d. What is the probability that the third voter supporting candidate Smith is reached on the fifth call, i.e., what is the probability that it takes the student five calls to reach three voters who supports candidate Smith?
Answers
The probabilities are calculated assuming independence of each call and that the success probability remains constant throughout the calls.
a. The probability that, among five voters the student calls, exactly one supports candidate Smith can be calculated using the binomial probability formula. With a success probability of 64% (0.64) and exactly one success (k = 1) out of five trials (n = 5), the probability can be calculated as follows:
\[
P(X = 1) = \binom{5}{1} \times (0.64)^1 \times (1 - 0.64)^4
\]
The calculation results in approximately 0.369, or 36.9%.
b. The probability that, among five voters the student calls, at least one supports candidate Smith can be calculated as the complement of the probability that none of the voters support Smith. Using the binomial probability formula, with a success probability of 64% (0.64) and no success (k = 0) out of five trials (n = 5), the probability can be calculated as follows:
\[
P(X \geq 1) = 1 - P(X = 0) = 1 - \binom{5}{0} \times (0.64)^0 \times (1 - 0.64)^5
\]
The calculation results in approximately 0.997, or 99.7%.
c. The probability that the first voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of not reaching a Smith supporter in the first four calls (0.36) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{First Smith Supporter on Fifth Call}}) = (1 - 0.64)^4 \times 0.64
\]
The calculation results in approximately 0.014, or 1.4%.
d. The probability that the third voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of reaching two Smith supporters in the first four calls (0.64 for the first call, 0.36 for the second call, and 0.36 for the third call) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{Third Smith Supporter on Fifth Call}}) = (0.64)^2 \times (1 - 0.64) \times 0.64
\]
The calculation results in approximately 0.147, or 14.7%.
know more about probabilities :brainly.com/question/29381779
#SPJ11
The probabilities are calculated assuming independence of each call and that the success probability remains constant throughout the calls. The calculation results in approximately 0.369, or 36.9%.
a. The probability that, among five voters the student calls, exactly one supports candidate Smith can be calculated using the binomial probability formula. With a success probability of 64% (0.64) and exactly one success (k = 1) out of five trials (n = 5), the probability can be calculated as follows:
[P(X = 1) = \binom{5}{1} \times (0.64)^1 \times (1 - 0.64)^4\]
The calculation results in approximately 0.369, or 36.9%.
b. The probability that, among five voters the student calls, at least one supports candidate Smith can be calculated as the complement of the probability that none of the voters support Smith. Using the binomial probability formula, with a success probability of 64% (0.64) and no success (k = 0) out of five trials (n = 5), the probability can be calculated as follows:
[P(X \geq 1) = 1 - P(X = 0) = 1 - \binom{5}{0} \times (0.64)^0 \times (1 - 0.64)^5\]
The calculation results in approximately 0.997, or 99.7%.
c. The probability that the first voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of not reaching a Smith supporter in the first four calls (0.36) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{First Smith Supporter on Fifth Call}}) = (1 - 0.64)^4 \times 0.64
\]
The calculation results in approximately 0.014, or 1.4%.
d. The probability that the third voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of reaching two Smith supporters in the first four calls (0.64 for the first call, 0.36 for the second call, and 0.36 for the third call) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{Third Smith Supporter on Fifth Call}}) = (0.64)^2 \times (1 - 0.64) \times 0.64
\]
The calculation results in approximately 0.147, or 14.7%.
know more about probabilities :brainly.com/question/29381779
#SPJ11
Q. A______ is a quadrilateral with two sets of parallel sides and 4 right angles
O trapezoid
O rectangle
O parallelogram
O square
Answers
Answer:
I think it will be rectangle or square
because rectangle and Square have 4 right angles
and each two opposite sides are parallel
DUE IN 10 MINUITES
solve for x

Answers
Answer: x = 20°
Step-by-step explanation:
These are vertical angles, which means they are congruent and equal to each other.
Given:
(4x + 30)° = 110°
Subtract 30° from both sides of the equation:
4x = 80°
Divide both sides of the equation by 4x:
x = 20°
Answer:x=20
Step-by-step explanation:
Vertical angles Theorem, this means that the two angles are equal to each other.
set equal.
4x+30=110
solve.
4x+30=110
-30 -30
4x=80
÷4 ÷4
x=20
identify an equation in point slope form for the line perpendiculae to y=1/4x-7 that passes through (-2,-6)
Answers
if the l 2l 2 norm of the vector aa is greater than the l 2l 2 norm of the vector bb, it is not always true that the l 1l 1 norm of aa is greater than the l 1l 1 norm of bb
Answers
The L1 norm of vector A is greater than or equal to the L1 norm of vector B.
How did we arrive at this assertion?Basically, if the L2 norm of vector A is greater than the L2 norm of vector B, it is indeed always true that the L1 norm of vector A is greater than or equal to the L1 norm of vector B. The Lp norm is defined as follows:
\(||x||_p = (|x_1|^p + |x_2|^p + ... + |x_n|^p)^(1/p),\)
where x = [x₁, x₂, ..., xₙ] is a vector.
For the L2 norm (p = 2), the formula is:
\(||x||_2 = \sqrt(|x_1|^2 + |x_2|^2 + ... + |x_n|^2).\)
For the L1 norm (p = 1), the formula is:
\(||x||₁ = |x_1| + |x_2| + ... + |x_n|.\)
If ||A||₂ > ||B||₂, it implies that:
\(\sqrt(|A_1|^2 + |A_2|^2 + ... + |A_n|^2) > \sqrt(|B_1|^2 + |B_2|^2 + ... + |B_n|^2).\)
Squaring both sides of the inequality, we get:
\(|A_1|^2 + |A_2|^2 + ... + |A_n|^2 > |B_1|^2 + |B_2|^2 + ... + |B_n|^2.\)
Since the squares of the magnitudes are positive, we can conclude that:
\(|A_1| + |A_2| + ... + |A_n| > |B_1| + |B_2| + ... + |B_n|.\)
Therefore, the L1 norm of vector A is greater than or equal to the L1 norm of vector B.
learn more about L1 norm of vector: https://brainly.com/question/28972644
#SPJ4
In the diagram below of triangle
F
G
H
FGH,
I
I is the midpoint of
F
H
‾
FH
and
J
J is the midpoint of
G
H
‾
GH
. If m
∠
H
F
G
=
57
−
6
x
∠HFG=57−6x, and m
∠
H
I
J
=
−
4
x
+
49
∠HIJ=−4x+49, what is the measure of
∠
H
I
J
∠HIJ
Answers
Applying the corresponding angles theorem, the measure of ∠HIJ = 33°.
What is the Corresponding Angles Theorem?If two triangles are similar to each other, their corresponding angles would be equal. Also, based on the corresponding angles theorem, corresponding angles are equal to each other.
Triangles IHJ and FGH are similar to each other, therefore, angles HFG and HIJ are corresponding angles.
Therefore:
The measure of angle HFG = the measure of angle HIJ
m∠HFG = 57 − 6x
m∠HIJ = −4x + 49
Thus:
57 − 6x = -4x + 49
Combine like terms
4x - 6x = -57 + 49
-2x = -8
Divide both sides by -2
-2x/-2 = -8/-2
x = 4
m∠HIJ = −4x + 49 = -4(4) + 49
m∠HIJ = 33°
Learn more about the corresponding angles theorem on:
https://brainly.com/question/28182407
#SPJ1
Complete Question:
In the diagram below of triangle FGH, I is the midpoint of FH and J is the midpoint of GH. If m∠HFG = 57 − 6x, and m∠HIJ = −4x + 49, what is the measure of ∠HIJ?

What is the equation of the line that passes through the point (5, – 7) and
has a slope of o?
Answers
Answer:
The answer is
\(y = - 7\)
Answer:
y = -7
Step-by-step explanation:
Hey :)
y = mx + b
*m is equal to the slope...
y = (0)x + b
Plug in the point you have...
-7 = (0) (5) + b
-7 = 0 + b
-7 = b
y = (0)x - 7
y = -7
Ignore the (0)x because anything multiplied by 0 is 0 so there's no point in having 0x in your equation.
Answer: y = -7
Hope this helps :)
assume that hamilton corporation has pre-tax income of $100,000, tax expense of $22,500, and an after-tax income of $77,500. what is hamilton effective tax rate?
Answers
Hamilton Corporation's effective tax rate is 22.5%.
The effective tax rate is a measure of a company's tax burden as a percentage of its pre-tax income. It indicates the proportion of pre-tax income that is paid in taxes.
In this case, Hamilton Corporation has a pre-tax income of $100,000 and a tax expense of $22,500. Therefore, the company paid $22,500 in taxes out of its pre-tax income of $100,000.
The effective tax rate is the ratio of the total tax expense to the company's pre-tax income.
Effective Tax Rate = Total Tax Expense / Pre-tax Income
In this case, the pre-tax income is $100,000, and the tax expense is $22,500. Therefore,
Effective Tax Rate = $22,500 / $100,000 = 0.225 or 22.5%
Learn more about effective tax rate here
brainly.com/question/29805701
#SPJ4
What is the rule that describes the translation that maps ΔLMN onto ΔL'M'N?

Answers
Answer:
3 united right and 4 units down
Step-by-step explanation:
the shape with the quotes- also called primes- is the second shape
AB is included between
A. BC and AC
B. AB and BC
C. ZB and ZC
D.A and B
Answers
Answer:
BC and AC are the answers
The classroom has 10 desks with boys and
girls. Show one combination of boys and
girls
Answers
Answer:
one combination could be 6 girls and 4 boys
a crossword game is played by two players. the game has 100 tiles and there is one letter on each tile. the 100 tiles are placed in a bag and mix thoroughly. the first player reaches in the bag and selects seven tiles. how different sets of 7 tiles can the first player choose?
Answers
Therefore, the first player can choose different sets of 7 tiles from 100 tiles, which are 160,075,608.
A crossword game is played by two players.
The game has 100 tiles, and there is one letter on each tile.
The 100 tiles are placed in a bag and mix thoroughly.
The first player reaches in the bag and selects seven tiles.
There are 100 tiles, and the first player selects seven tiles.
The first player can choose different sets of 7 tiles in the following ways:
100 C 7 = 160,075,608.
This is the formula for the combination of 7 items out of 100 items.
Combination: Combination is defined as the way of choosing r things from n different things without considering the order.
The number of possible combinations is given by nCr.
Where nCr is defined as\(\[\frac{n!}{r!(n-r)!}\]n!\) represents factorial, which is the multiplication of all the natural numbers from 1 to n.
A factorial is defined as an integer that is multiplied by all of the positive integers less than.
In mathematics, the factorial of a non-negative integer n is the product of all positive integers less than or equal to n. It is denoted by n!
For example: 5! = 5 × 4 × 3 × 2 × 1
= 1204!
= 4 × 3 × 2 × 1 = 24.
For similar question on sets.
https://brainly.com/question/13458417
#SPJ11
Hello I need help for this math homework please

Answers
Answer:
1. first option
2. second option
3. second option
Step-by-step explanation:
i dunno i did the math and used a calculator. im pretty confident with my answers so hopefully theyre right
Choose all the expressions that have 2/3 as a product
Answers
The expressions that have 2/3 as the product are A. \(\frac{4}{5}\times\frac{5}{6}\) and E. \(\frac{6}{7}\times\frac{7}{9}\). These are calculated by the simplification method.
The product is obtained by the multiplication of two or more other numbers together. For example, let us consider two numbers 2 and 9. Multiply these two numbers. We get 27. This number is considered the product of the two numbers 3 and 9.
To find whether the given expression has a product as 2/3, perform simplification for the given expressions.
Simplifying the first expression,
\(\begin{aligned}\frac{4}{5}\times\frac{5}{6}&=\frac{4}{6}\\&=\frac{2}{3}\end{aligned}\)
Simplifying the second expression,
\(\begin{aligned}\frac{7}{8}\times\frac{9}{10}=\frac{63}{80}\end{aligned}\)
Simplifying the third expression,
\(\begin{aligned}\frac{1}{3}\times\frac{2}{3}=\frac{2}{9}\end{aligned}\)
Simplifying the fourth expression,
\(\begin{aligned}\frac{3}{4}\times\frac{7}{12}=\frac{7}{16}\end{aligned}\)
Simplifying the fifth expression,
\(\begin{aligned}\frac{6}{7}\times\frac{6}{9}&=\frac{6}{9}\\&=\frac{2}{3}\end{aligned}\)
The required answer is options A and E.
To know more about simplification:
https://brainly.com/question/11589761
#SPJ4
The complete question is -
Choose all the expressions that have \(\frac{2}{3}\) as a product
A. \(\frac{4}{5}\times\frac{5}{6}\)
B. \(\frac{7}{8}\times\frac{9}{10}\)
C. \(\frac{1}{3}\times\frac{2}{3}\)
D. \(\frac{3}{4}\times\frac{7}{12}\)
E. \(\frac{6}{7}\times\frac{7}{9}\)
problem: a radio tower is located 615 feet from a building. from a window in the building, a person determines that the angle of elevation to the top of the tower is 42 degrees and that the angle of depression to the bottom of the tower is 34 degrees. how tall is the tower in exact form (in terms of the trig functions) and to the nearest integer?
Answers
The height of the tower is 969 feet.
Let CD be the tower and A be the point from a window in the building, a person determines that the angle of elevation to the top of the tower is 42 degrees.
In triangle AED
tan42° = ED/AE
tan42° = h₁/615
h₁ = tan42° × 615
= 553.74
Rounding to the nearest integer
h₁ = 554
In triangle AEC
tan34° = EC/AE
tan34° = h₂/615
h₂ = tan34° × 615
= 414.82
Rounding to the nearest integer
h₂ = 415
Height of tower = EC + ED
= h₁ + h₂
= 554 + 415
= 969
Therefore, the height of the tower is 969 feet.
Learn more about angle of elevation here:
brainly.com/question/21137209
#SPJ4

A cylinder has a height of 13 meters. It's volume is 4,082 cubic meters. What is radius of the cylinder?
Answers
Answer: A cylindrical water storage tank has an inside base radius of 7m and depth of 11 m. ... Let the depth of the tank be h metres.
Step-by-step explanation:
Answer:
the radius is 10 m apprx
Step-by-step explanation:
height of the cylinder = \(\pi r^{2} h\) = 4082 \(m^3\)
then \(r^{2}= \frac{4082}{13\pi } = 99.9493\)
r= \(\sqrt{99.9493}\) =10.0 m
A toy store sells individual marbles in a variety of colors and sizes.
What is the probability that a randomly selected marble is purple or small?

Answers
The probability that a randomly selected marble is purple or small is: 0.5254
How to find the probability from the table?The total number of big marbles = 34 marbles
The total number of small marbles = 25 marbles
The total number of red marbles = 22 marbles
The total number of Green Marbles = 11 marbles
The total number of purple marbles = 16 marbles
The total number of blue marbles = 10 marbles
Total number of all marbles = 59 marbles
Thus, the probability that a randomly selected marble is purple or small is:
P(purple or small) = (16/59) + (25/59)
= 31/59 = 0.5254
Read more about probability table at: https://brainly.com/question/27899440
#SPJ1
1) If ∑Cn(x–3)^n converges at x=7 and diverges at x=10, what can you say about the convergence at x=11? At x=5? At x=0?
Answers
At x=0, we can say that the series ∑\(Cn(X - 3)^n\) converges, as the given condition for convergence is satisfied at x=7, x=10, and x=0 is between the two values.
At x=11, we can say that the series ∑\(Cn(X - 3)^n\) converges, as the given condition for convergence is satisfied at x=7 and x=11 is between the two values. At x=5, we can say that the series ∑\(Cn(X - 3)^n\) diverges, as the given condition for convergence is not satisfied at x=5.
The theory behind the question is the idea of a power series, which is an infinite series of terms where each term is a power of a variable raised to a constant. In this case, we have a series of the form:
\(Cn(X - 3)^n\)
here Cn is a constant. The question is asking about the behavior of this series as a function of the variable x, specifically whether it converges or diverges. The condition for convergence of a power series is that the absolute value of the coefficients (i.e., the absolute value of Cn) must be less than or equal to 1 for all values of x in the interval where the series is defined. If this condition is satisfied, then the series converges.
Learn more about convergence visit: brainly.com/question/30114464
#SPJ4
The function f(x) = 4x + 10 models the amount of money francis makes when babysitting for x hours. How much money will he make for 2 hours of babysitting work?.
Answers
The amount of money that he will make for 2 hours of baby sitting work is $18
The function is
f(x) = 4x + 10
The function f(x) is the amount of money Francis makes when babysitting for x hours
The function is the mathematical statement that shows the relationship between one variable and another variable. If one variable is dependent variable then the other variable will independent variable
The function
f(x) = 4x + 10
The number of hours x = 2 hours
Substitute the values of x in the function
f(2) = 4(2) + 10
f(2) = 8 +10
f(2) = $18
Hence, the amount of money that he will make for 2 hours of baby sitting work is $18
Learn more about function here
brainly.com/question/20534410
#SPJ4
Please help me for question 12.

Answers
Answer:
79°
Step-by-step explanation:
its a right angled triangle so the unknown is 90°
180 - (90 + 11)
if a scale drawing uses a scale of 1:12, what would 2 1/2 inches on the model represent in real life?
2/12 feet.
4/10 feet
30 feet
4 4/5
Answers
2.5 x 12 = 30
final answer = 30
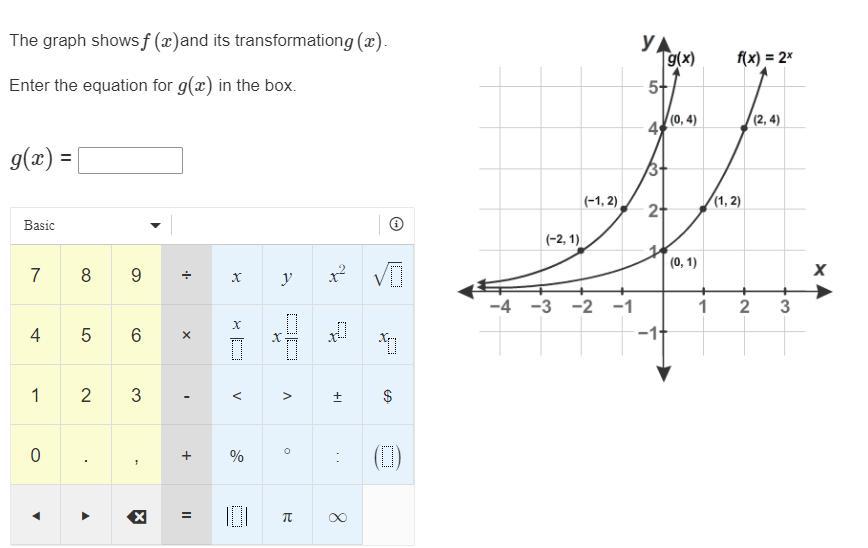
Please help me with this question so I can better help my son to understand this better. I have attached the graph that were working from below? The graph shows f(x)and its transformation g(x).Enter the equation for g(x) in the box.g(x) =
Answers
Answer
g(x) = 2ˣ⁺² or 2^(x + 2)
\(g(x)=2^{x+2}\)
Explanation
When a function f(x) is translated horizontally along the x-axis by a units, the new function is represented as
f(x + a) when the translation is by a units to the left.
f(x - a) when the translation is by a units to the right.
Looking at the coordinates of the points given on f(x) and g(x), we can see that g(x) is just f(x) translate 2 units to the left.
Hence, if f(x) = 2ˣ
g(x) = f(x + 2) = 2ˣ⁺² or 2^(x + 2)
Hope this Helps!!!
What is AC?
А
А
D
5
B

Answers
why is x^2-8x+20 always positive?
Answers
Answer:
cause it is
Step-by-step explanation:
it just is, sorry i can't help. maybe bc there are more positive functions then negative ones?