Answers
We know that one yards is 36 inches, then to determine how many inches 5 yards are we just multiply 5 by 36, then we have:
\(5\cdot36=180\)Therefore 5 yards is 180 inches.
Related Questions
please hurry if you can. A gift in a cubic box with 15 inches edge lengths needs to be wrapped.
How many square inches of wrapping paper will be needed to cover the box?
Question 3 options:
2250 in2
1350 in2
3375 in2
Answers
Answer:
1350 in^2
Step-by-step explanation:
In order to solve this question, you need to find the surface area of the box. This is because the box needs to be covered by wrapping paper.
1. Formula for the surface area of a cube: A=6x^2, in which x represents the length of the cube.
2. Plug in 15 as x and solve.
A=6(15^2)
A=6(225)
A=1350
Toby created a sculpture for art class using different-sized cubes. The smallest cube is 1.5 inches along each edge. The largest cube is 7.5 inches along each edge.
How many of the smallest cubes would it take to fill the largest cube?
Write your answer as a whole number or decimal. Do not round.
Answers
There are 125 of the smallest cubes that will fill the largest cube using the size of their respective volume
Volume of cubeThe volume of cube is calculated by using a × a × a = a³ where "a" is the edge.
The volume of the smallest cube = 1.5inches × 1.5inches × 1.5inches
The volume of the smallest cube = 3.375inches³
The volume of the largest cube = 7.5inches × 7.5inches × 7.5inches
The volume of the largest cube = 421.875inches³
Thus, the number of the smallest cubes it would take to fill the largest cube is derived by
421.875inches³/3.375inches³ = 125.
Know more about volume here:https://brainly.com/question/1972490
#SPJ1
DUE REALLY SOON SOMEONE PLEASE HELP ME WITH THIS!

Answers

Find the point P on the graph of the function y=√x closest to the point (9,0)
The x coordinate of P is:
Answers
Answer:
\(\displaystyle \frac{17}{2}\).
Step-by-step explanation:
Let the \(x\)-coordinate of \(P\) be \(t\). For \(P\!\) to be on the graph of the function \(y = \sqrt{x}\), the \(y\)-coordinate of \(\! P\) would need to be \(\sqrt{t}\). Therefore, the coordinate of \(P \!\) would be \(\left(t,\, \sqrt{t}\right)\).
The Euclidean Distance between \(\left(t,\, \sqrt{t}\right)\) and \((9,\, 0)\) is:
\(\begin{aligned} & d\left(\left(t,\, \sqrt{t}\right),\, (9,\, 0)\right) \\ &= \sqrt{(t - 9)^2 +\left(\sqrt{t}\right)^{2}} \\ &= \sqrt{t^2 - 18\, t + 81 + t} \\ &= \sqrt{t^2 - 17 \, t + 81}\end{aligned}\).
The goal is to find the a \(t\) that minimizes this distance. However, \(\sqrt{t^2 - 17 \, t + 81}\) is non-negative for all real \(t\!\). Hence, the \(\! t\) that minimizes the square of this expression, \(\left(t^2 - 17 \, t + 81\right)\), would also minimize \(\sqrt{t^2 - 17 \, t + 81}\!\).
Differentiate \(\left(t^2 - 17 \, t + 81\right)\) with respect to \(t\):
\(\displaystyle \frac{d}{dt}\left[t^2 - 17 \, t + 81\right] = 2\, t - 17\).
\(\displaystyle \frac{d^{2}}{dt^{2}}\left[t^2 - 17 \, t + 81\right] = 2\).
Set the first derivative, \((2\, t - 17)\), to \(0\) and solve for \(t\):
\(2\, t - 17 = 0\).
\(\displaystyle t = \frac{17}{2}\).
Notice that the second derivative is greater than \(0\) for this \(t\). Hence, \(\displaystyle t = \frac{17}{2}\) would indeed minimize \(\left(t^2 - 17 \, t + 81\right)\). This \(t\!\) value would also minimize \(\sqrt{t^2 - 17 \, t + 81}\!\), the distance between \(P\) \(\left(t,\, \sqrt{t}\right)\) and \((9,\, 0)\).
Therefore, the point \(P\) would be closest to \((9,\, 0)\) when the \(x\)-coordinate of \(P\!\) is \(\displaystyle \frac{17}{2}\).
random sample has been taken from a normal population and two confidence intervals constructed using exactly the same data. The two CIs are (38.02, 61.98) and (39.95, 60.05). (a) What is the value of the sample mean
Answers
The sample mean of the random sample is 50
The margin of error (E) is the amount of error allowed in the random sample.
The confidence interval (CI) is given by:
CI = μ ± E = (μ - E, μ + E)
Given a confidence interval of (38.02, 61.98), hence:
μ - E = 38.02 (1)
μ + E = 61.98 (2)
Hence solving equations 1 and 2 simultaneously gives:
μ = 50, E = 11.98
Hence the sample mean of the random sample is 50
Find out more at: https://brainly.com/question/24131141
A teaching hospital in South-West Part of Nigeria receives on the average 5 pregnant women with high blood pressure per week. What is the probability that on a particular week, the teaching hospital will receive:
1.) No high BP pregnant woman
Answers
Answer:
The probability that on a particular week, the hospital will receive on high BP pregnant woman is 0.0068
Step-by-step explanation:
We use the Exponential distribution,
Since we are given that on average, 5 pregnant women with high blood pressure come per week,
So, average = m = 5
Now, on average, 5 people come every week, so,
5 women per week,
so, we get 1 woman per (1/5)th week,
Hence, the mean is m = 1/5 for a woman arriving
and λ = 1/m = 5 = λ
we have to find the probability that it takes higher than a week for a high BP pregnant woman to arrive, i.e,
P(X>1) i.e. the probability that it takes more than a week for a high BP pregnant woman to show up,
Now,
P(X>1) = 1 - P(X<1),
Now, the probability density function is,
\(f(x) = \lambda e^{-\lambda x}\)
And the cumulative distribution function (CDF) is,
\(CDF = 1 - e^{-\lambda x}\)
Now, CDF gives the probability of an event occuring within a given time,
so, for 1 week, we have x = 1, and λ = 5, which gives,
P(X<1) = CDF,
so,
\(P(X < 1)=CDF = 1 - e^{-\lambda x}\\P(X < 1)=1-e^{-5(1)}\\P(X < 1)=1-e^{-5}\\P(X < 1) = 1 - 6.738*10^{-3}\\P(X < 1) = 0.9932\\And,\\P(X > 1) = 1 - 0.9932\\P(X > 1) = 6.8*10^{-3}\\P(X > 1) = 0.0068\)
So, the probability that on a particular week, the hospital will receive on high BP pregnant woman is 0.0068
what value of c make polynamial below a prefect square ? x^2+10x+c
C=
Answers
Answer:
the value of c is 25
Step-by-step explanation:
b/2a= 10/2(1)= 10/2= 5
(5)^2 = 25
x^2 + 10x + 25 = (x + 5)^2
need help with that answer

Answers
For you to make 5 pecan pies, it would be necessary to buy 1.9 pounds of pecans.
How many grams are there in a cup of pecans?Based on the information displayed on the label 1 cup of pecans is equal to 99 grams.
How many pounds do you need for 5 pecan pies?We know 1 pecan pie requires 1 3/4 cups or 1.75 cups (3/4 = 0.75)
1.75 x 5 = 8.75 cups in total
Now, let's calculate this in grams:
8.75 x 99 = 866.22 grams
Finally, let's calculate the pounds
1 pound = 453
x = 866.22
x = 866.22 / 453 = 1.9
Learn more about ratios in https://brainly.com/question/13419413
#SPJ1
Six is fifteen less than three time a number
Answers
Answer:
3x-15=6
Step-by-step explanation:
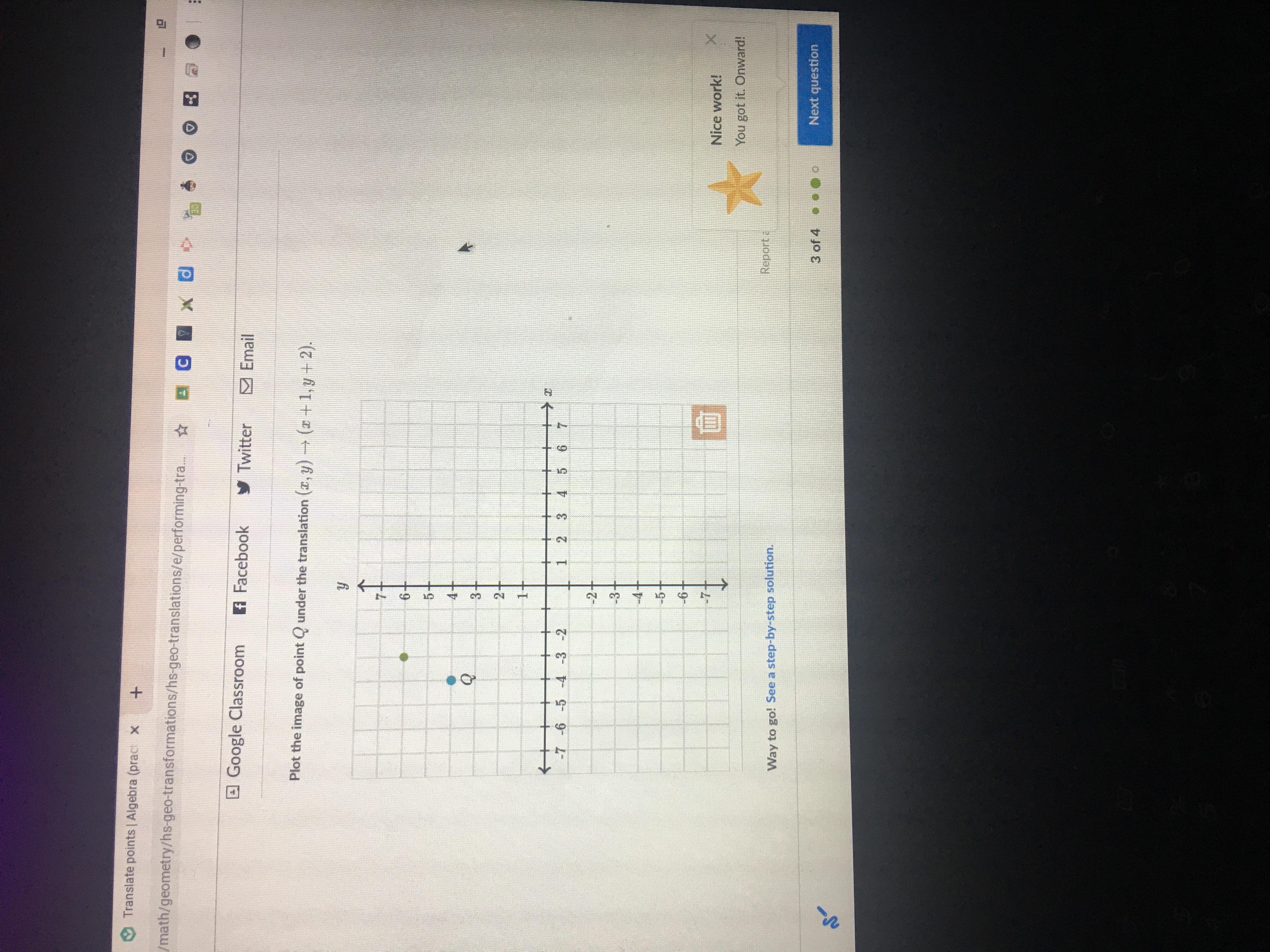
Plot the image of point QQQ under the translation (x,y)\to(x+1,y+2)(x,y)→(x+1,y+2)left parenthesis, x, comma, y, right parenthesis, \to, left parenthesis, x, plus, 1, comma, y, plus, 2, right parenthesis.
Answers
The coordinates of the image of the point Q is Q'(3, 6).
What is Geometric Transformation?Transformation of geometrical figures or points is the manipulation of a given figure to some other way.
Different types of transformations are Rotation, Reflection, Glide reflection, Translation and Dilation.
From the given graph, we have point Q(-4, 4).
Here the point is translated.
After translation, the original figure is shifted from a place to another place without affecting it's size.
The rule of translation is given as the point (x, y) is translated as (x + 1, y + 2).
So the given point is (-4, 4).
(-4, 4) after translation becomes by the definition (-4 + 1, 4 + 2).
So the required point is (-3, 6).
Hence the image of point Q is (-3, 6).
To learn more about Translation, click on the link given below :
https://brainly.com/question/12463306
#SPJ1
Your question is incomplete, Probably, the correct graph for the question is given below.
what is difactorization
Answers
Answer:
do u mean factorization?
if so, In math, factorization is when you break a number down into smaller numbers that, multiplied together, give you that original number. When you split a number into its factors or divisors, that's factorization. For example, factorization of the number 12 might look like 3 times 4.
Step-by-step explanation:
Hope this helps!
Answer: it an operation of resolving a quantity into factors; also : a product obtained by factorization
Step-by-step explanation: hope i help
The area of a square is 36 sq.cm, then its perimeter is a) 24 cm b) 6 cm c) 144 cm d) 36 cm
Answers
Answer:
Step-by-step explanation:
3.6*
It is very easy to find the perimeter of a square when its area is given in the question. For that, you only ned to know one fomula. That formula is: Area = side^2
For this particular question, the given value for the area of the square is 36 sq.cm. So, we can solve for the side(s) by substituting the given value in the above mentioned formula.
We get
36 = s^2
Now, we need to get the square root of both sides, which gives us
s = √36 s = 6 cm
Since all the sides of a square are equal in length, the side length is 6 cm. Now to determine the perimeter, we must multiply the side length by 4 (because there are 4 equal sides in a square). That gives us Perimeter = 4 x side length Perimeter = 4 x 6 cm.
Therefore, the perimeter of the square is 24 cm.
Check this out-
https://brainly.com/question/29192128?referrer=searchResults
culate wages and taxes
Mr Singh is paid £11.70 per hour after tax is deducted.
a) How much does he earn if he works 5 hours?
b) How much does he earn if he works 10 hours?
c) He works 37.5 hours per week.
How much does he earn in a week?
Please help!
Answers
Answer:
a) £58.5
b) £117
c) £438.75
Step-by-step explanation:
Mr Singh is paid £11.70 per hour after tax is deducted.
This means that for x hours of work, his earning are given by:
\(E(x) = 11.7x\)
a) How much does he earn if he works 5 hours?
This is E(5).
\(E(5) = 11.7*5 = 58.5\)
b) How much does he earn if he works 10 hours?
This is E(10).
\(E(10) = 11.7*10 = 117\)
c) He works 37.5 hours per week. How much does he earn in a week?
This is E(37.5).
\(E(37.5) = 11.7*37.5 = 438.75\)
HELP ON TIMER!!!
Which could be the missing first term of the expression that, when fully simplified, would be a binomial with a degree of 4? Select three options.
0
5xy^3
9x^2 y
8y^4
4xy^3
Answers
Hope it works :)
The solution is, the last possibility is 9x^2 y – 5xy3 + 9x2y =18x^2 y – 5xy3, binomial degree 4.
What are Polynomials?Polynomials are sums of k-xⁿ terms, where k can be any number and n can be any positive integer.
here, we have,
First, if we have a polynomial that the form is as follow
P(x,y)=a1x^n-1y^p-1+ a2x^n-2y^p-2 + . . . . + a0xy+c,
the degree can be found with the sum of the highest value of power of each term.
If the number of term is 3, it is called trinomial, if it is 2, the polynomial is called binomial.
So in our case, 0– 5xy3 + 9x2y is a binomial with a degree of 4, because number of term 2, degree =1 + 2 =3, upper than 2+ 1(the second term) 4xy^3– 5xy3 + 9x2y = -xy3 +9x2y, binomial degree 4,
and the last possibility is 9x^2 y – 5xy3 + 9x2y =18x^2 y – 5xy3, binomial degree 4.
Hence, The solution is, the last possibility is 9x^2 y – 5xy3 + 9x2y =18x^2 y – 5xy3, binomial degree 4.
Know more about Polynomials here:
brainly.com/question/2833285
#SPJ5
Please answer this correctly without making mistakes

Answers
1127 x 2 = 2254
1 x 2 = 2
so that’s 2,254 cups & 2 fl. ounces
since 8 fl. oz. make a cup, and we only have 2, the answer stays as it is
2,254 cups & 2 fl. ounces
#3 Preimage point B is
located at (5,-4).
B' is located at (20, -16).
Write the algebraic rule for
the transformation.
Answers
The algebraic rule for the transformation is B' = (Bx + 15, By - 12)
Given data ,
To determine the algebraic rule for the transformation from point B to point B', we need to find the equations that relate the coordinates of the preimage point B to the image point B'.
Let's denote the translation amounts in the x-direction and y-direction as (dx, dy). The coordinates of B' can be obtained by adding these translation amounts to the coordinates of B:
B' = (Bx + dx, By + dy)
Given that B is located at (5, -4) and B' is located at (20, -16), we can calculate the translation amounts:
dx = 20 - 5 = 15
dy = -16 - (-4) = -12
Hence , the algebraic rule for the transformation is B' = (Bx + 15, By - 12)
To learn more about translations click :
https://brainly.com/question/19007400
#SPJ1
p+12=17 what does p equal in this situation
Answers
Answer:
5
Step-by-step explanation:
5+12= 17
Equation/Question:
P+12=17 What does P equal in this situation?
Answer/Steps to answer:
1. Subtract 12 from both sides.
p=17-12
2. Simplify 17-12 to 5.
p=5
-------------------
Checking:
P+12=17
1. Let p=5.
5+12=17
2. Simplify 5+12 to 17.
17=17
Done by NeighborhoodDealer
Non Shaded Shaded
Area
Area
8
Find the radius
of the small circle

Answers
Answer:
The answer is 16pi or 50.3cm² to 1 d.p
Step-by-step explanation:
The non shaded=area of shaded
d=8
r=d/2=4
A=pir³
A=p1×4²
A=pi×16
A=16picm² or 50.3cm² to 1d.p
Answer:
3.45 cm (3 s.f.)
Step-by-step explanation:
We have been given a 5-sided regular polygon inside a circumcircle. A circumcircle is a circle that passes through all the vertices of a given polygon. Therefore, the radius of the circumcircle is also the radius of the polygon.
To find the radius of a regular polygon given its side length, we can use this formula:
\(\boxed{\begin{minipage}{6 cm}\underline{Radius of a regular polygon}\\\\$r=\dfrac{s}{2\sin\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}\)
Substitute the given side length, s = 8 cm, and the number of sides of the polygon, n = 5, into the radius formula to find an expression for the radius of the polygon (and circumcircle):
\(\begin{aligned}\implies r&=\dfrac{8}{2\sin\left(\dfrac{180^{\circ}}{5}\right)}\\\\ &=\dfrac{4}{\sin\left(36^{\circ}\right)}\\\\ \end{aligned}\)
The formulas for the area of a regular polygon and the area of a circle given their radii are:
\(\boxed{\begin{minipage}{6 cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{nr^2\sin\left(\dfrac{360^{\circ}}{n}\right)}{2}$\\\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}\)
\(\boxed{\begin{minipage}{6 cm}\underline{Area of a circle}\\\\$A=\pi r^2$\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}\)
Therefore, the area of the regular pentagon is:
\(\begin{aligned}\textsf{Area of polygon}&=\dfrac{5 \cdot \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\sin\left(\dfrac{360^{\circ}}{5}\right)}{2}\\\\&=\dfrac{5 \cdot \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\sin\left(72^{\circ}\right)}{2}\\\\&=\dfrac{\dfrac{80\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}}{2}\\\\&=\dfrac{40\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}\\\\&=110.110553...\; \sf cm^2\end{aligned}\)
The area of the circumcircle is:
\(\begin{aligned}\textsf{Area of circumcircle}&=\pi \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\\\\&=\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\&=145.489779...\; \sf cm^2\end{aligned}\)
The area of the shaded area is the area of the circumcircle less the area of the regular pentagon plus the area of the small central circle.
The area of the unshaded area is the area of the regular pentagon less the area of the small central circle.
Given the shaded area is equal to the unshaded area:
\(\begin{aligned}\textsf{Shaded area}&=\textsf{Unshaded area}\\\\\sf Area_{circumcircle}-Area_{polygon}+Area_{circle}&=\sf Area_{polygon}-Area_{circle}\\\\\sf 2\cdot Area_{circle}&=\sf 2\cdot Area_{polygon}-Area_{circumcircle}\\\\2\pi r^2&=2 \cdot \dfrac{40\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}-\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\2\pi r^2&=\dfrac{80\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}-\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\\end{aligned}\)
\(\begin{aligned}2\pi r^2&=\dfrac{80\sin\left(72^{\circ}\right)-16\pi}{\sin^2\left(36^{\circ}\right)}\\\\r^2&=\dfrac{40\sin\left(72^{\circ}\right)-8\pi}{\pi \sin^2\left(36^{\circ}\right)}\\\\r&=\sqrt{\dfrac{40\sin\left(72^{\circ}\right)-8\pi}{\pi \sin^2\left(36^{\circ}\right)}}\\\\r&=3.44874763...\sf cm\end{aligned}\)
Therefore, the radius of the small circle is 3.45 cm (3 s.f.).

Ten upright dominos of increasing height are lined up to be knocked down. The dominos are numbered 0 to 9. The smallest domino, #0, is 3.00 inches tall and will be toppled by a person to start the chain reaction. Each subsequent domino is 15% taller than the one before. What is the height of domino #9?
Answers
Answer:
8.604 in.
Step-by-step explanation:
We can use the formula for compound interest to find the height of domino #9:
A = P(1 + r)^n
where A is the final amount, P is the initial amount, r is the growth rate, and n is the number of compounding periods. In this case, P is the height of domino #0, r is 15% or 0.15, and n is 9 (since we want to find the height of domino #9).
Substituting the given values:
A = 3.00 in * (1 + 0.15)^9
Simplifying:
A = 3.00 in * 2.86797199
A ≈ 8.604 in
Therefore, the height of domino #9 is approximately 8.604 inches.
solve pls brainliest

Answers
In coordinates, the first number is the x and the second one is y. In (4,2), 4 is the x and 2 is the y. The x axis goes from left to right and the y axis goes from up to down.

A coffee shop serves an average of 72 customers per hour during the morning rush. Find the probability that less than 59 customers arrive in an hour during tomorrow's morning rush.
Answers
The probability that less than 59 customers arrive in an hour during tomorrow's morning rush will be 0.0521.
How to calculate the probability?From the information given, it was stated that coffee shop serves an average of 72 customers per hour during the morning rush and we eat to find the probability that less than 59 customers arrive in an hour during tomorrow's morning rush.
This will be done by using the Poisson distribution:
P(x <= 58) = [e^-72 × (72)^x]/x!
= 0.0521
Therefore, the probability that less than 59 customers arrive in an hour during tomorrow's morning rush will be 0.0521.
Learn more about probability on:
brainly.com/question/24756209
#SPJ1
Help plz:)))I’ll mark u Brainliest 0-o

Answers
Answer: x=9
Step-by-step explanation:
Find all exact solutions on [0, 2π). (Enter your answers as a comma-separated list.)
tan(x) − 2 sin(x) tan(x) = 0.
Answers
Answer:
\(0, \dfrac{\pi}{6}, \dfrac{5\pi}{6}, \pi\)
Step-by-step explanation:
Given the equation:
\(sin(x)-2sin(x) tan(x)=0\)
To find:
The solutions of given equation in the range [0, 2\(\pi\)) i.e. 0 can be in the answer but \(2\pi\) can not be there in the answer.
Solution:
Taking \(tan(x)\) common, we get:
\(tan(x) (1-2sin(x))=0\)
The solutions can be given as:
\(tan(x) = 0\) OR \(1-2sin(x) = 0\)
Let us solve both the equations one by one:
First equation:
\(tan(x) = 0\\ \Rightarrow x=0, \pi\)
Second equation:
\(1-2sin(x) = 0\\\Rightarrow 2sinx=1\\\Rightarrow sinx=\dfrac{1}{2}\\\Rightarrow x = \dfrac{\pi}{6}, \dfrac{5\pi}{6}\)
Therefore, the answers as a comma separated list are:
\(0, \dfrac{\pi}{6}, \dfrac{5\pi}{6}, \pi\)
what is mXY based on the figure shown

Answers
Answer: 120 degrees
78 + 42 = 120
A bag contains 10 balls of which 6 are red and the rest white and blue of equal numbers. If a ball is picked at random, find the probability that it is either white or red.
Answers
Answer:
Since each ball has an equal chance of being drawn: 16 p = 1, or ... You can either apply the first equation to find that. B = 1 - R = 3/8 ... A box contains 5 white, 6 red, and 4 black balls of identical size. If 3 balls are ... What is the probability of getting 2 red balls if we pick 3 balls from the bag randomly
Step-by-step explanation:
Answer:
\(\frac{4}{5}\)
Step-by-step explanation:
Let \(w\) = number of white balls, \(b\) = number of blue balls
6 + \(w\) + \(b\) = 10
\(w\) + \(b\) = 4
\(\because\) \(w\) = \(b\)
\(\therefore\) \(w\) + \(b\) =
\(w\) = \(2\)
\(P\)(\(r\)∪\(w\)) = \(P(r) + P(w) - P(r\)∩\(w)\)
= \(\frac{6}{10} + \frac{2}{10} - \frac{0}{10}\)
= \(\frac{8}{10}\)
= \(\frac{4}{5}\)
\(\therefore\) The probability of picking either a red or white ball is \(\frac{4}{5}\)
Hope this helps :)
Which could describr the motion of an object in distance and displacement
Answers
Answer:
Hope this will help you :)
Step-by-step explanation:

a summer soccer cam ordered a total of 84 soccer balls and t-shirts for the season. Soccer balls cost $25 each and t-shirts cost $9.50 each. if they paid $1,046 total for the purchase, how many of each item was ordered?
Answers
The Number of Soccer Balls is 16 and the Number of T-Shirts is 68
What is Linear Equation in Two Variables?
A linear equation in two variables is one that is stated in the form ax + by + c = 0, where a, b, and c are real integers and the coefficients of x and y, i.e. a and b, are not equal to zero.
Solution:
Let,
Number of Soccer Balls = x
Number of T-Shirts = y
Equation 1:
x + y = 84 -----------(i)
Equation 2:
25x + 9.5y = 1046 ----------(ii)
Multiplying Equation 1 by 25
25x + 25y = 2100 ---------(iii)
Substracting Equation2 from Equation 1
15.5y = 1054
y = 68
So, x = 16
To learn more about Linear Equation in Two Variables from the given link
https://brainly.com/question/24085666
#SPJ1
how does the parent function graphed below differ from the graph of the parent function, f(x)=x?

Answers
To answer this question let's graph the parent function f(x)=x.
Now that we have the parent function we can compare both graphs.
We notice that the function given is translated 3 units up. Therefore the answer is B.

Identify the kind of sample that is described. A researcher asked a simple random sample of home-schooled children, a simple random sample of children who attend private school, and a simple random sample of children who attend public school their opinion on the new town curfew.
Answers
Answer:
stratified sample
Step-by-step explanation:
The kind of sample that is being described is known as a stratified sample. This would be the type of sample because the researchers are dividing the entire student population that exists into various different categories or groups. The groups that have been created are home-schooled students, private school students, and public school students. All of the students are still part of the student population and therefore represent their groups.
(True/False) Economists and accountants usually disagree in the inclusion of implicit costs into the cost analysis of a firm.
Answers
The statement "Economists and accountants usually disagree in the inclusion of implicit costs into the cost analysis of a firm " is true
Accountants are the peoples who track the flow of money for the individuals and the business activities. But the Economist track the largest trends that use the money and resources of the company
So the view of the Economist and accountant on cost is different, because both of them are seeing the cost analysis of the company in different ways. So it possible that the Economists and accountants disagree in the inclusion of implicit cost
Therefore, the given statements is true
Learn more about flow of money here
brainly.com/question/14404699
#SPJ4
