(5-t-t^4)(9t+t^2)pls help
Answers
- ( t⁶ + 9t⁵ + t³ + 4t² - 45t )
Step-by-step explanation:Hi there !
(5 - t - t⁴)(9t + t²) =
= 45t + 5t² - 9t² - t³ - 9t⁵ - t⁶
= 45t - 4t² - t³ - 9t⁵ - t⁶
= - ( t⁶ + 9t⁵ + t³ + 4t² - 45t )
Good luck !
Related Questions
Please help
For b: T=b/2-g
Answers
Answer:
Step-by-step explanation:
b/(2 - g) = T
(2 - g)(b/(2-g) = T)
b = T(2 - g)
Two independent events, A and B, are such that P(A) = 0. 2 P(A U B) = 0. 8
(a) (i) Find P
(B) (ii) Find P(ANB)
b) State, with a reason, whether or not the events A and B are mutually exclusive.
Answers
(A) If Two independent events, A and B, are such that P(A) = 0. 2 P(A U B) = 0. 8, then probability P(B) = 5/8.
What is probability?The possibility of the result of any random event is referred to as probability. This term refers to determining how likely an event is to occur. What are the chances of getting a head when we toss a coin in the air, for instance? The quantity of outcomes depends on the response to this question. Here, the outcome could be either head or tail. Thus, there is a 50% chance that the result will be a head.
The probability serves as a gauge for the likelihood that an event will occur. It gauges how likely an event is to occur. The probability equation is given by;
P(E) = Number of Favourable Outcomes/Number of total outcomes
We know that
P(A∪B) = P(A) + P(B) - P(A∩B)
P(A∪B) = P(A) + P(B) - P(A).P(B)
0.8 = 0.2 + P(B) - 0.2.P(B)
0.5 = P(B) - 0.2.P(B)
0.5 = 0.8.P(B)
P(B) = 0.5/0.8
P(B) = 5/8
Learn more about probability
https://brainly.com/question/24756209
#SPJ4
What is the surface area of the right rectangular prism?

Answers
Answer:
Hello! answer: 250
Step-by-step explanation:
10 × 5 = 50
10 × 5 = 50
10 × 5 = 50
10 × 5 = 50
5 × 5 = 25
5 × 5 = 25
50 × 4 = 200
200 + 25 + 25 = 250 the total surface area is 250 hope that helps!
1/2x - 1/4 and 5x^2 - 2x + 6 ( show in standard form and explain how did you get it)
Answers
The standard form is given by(As highest degree is 2 we will take till degree 2 i.e quadratic)
ax²+bx+cSo
#1
1/2x-1/40x²+1/2x-1/4Multiply 4
0x²+2x-1Here
a=0b=2c=-1#2
5x²-2x+6Already in standard form
a=5b=-2c=6Answer:
\(\dfrac{5}{2}x^3-\dfrac{9}{4}x^2+\dfrac{7}{2}x-\dfrac{3}{2}\)
Step-by-step explanation:
The product of the two expressions is:
\(\left(\dfrac{1}{2}x-\dfrac{1}{4}\right)(5x^2-2x+6)\)
\(=\dfrac{1}{2}x(5x^2-2x+6)-\dfrac{1}{4}(5x^2-2x+6)\)
\(=\dfrac{5}{2}x^3-\dfrac{2}{2}x^2+\dfrac{6}{2}x-\dfrac{5}{4}x^2+\dfrac{2}{4}x-\dfrac{6}{4}\)
\(=\dfrac{5}{2}x^3-x^2-\dfrac{5}{4}x^2+3x+\dfrac{1}{2}x-\dfrac{3}{2}\)
\(=\dfrac{5}{2}x^3-\dfrac{9}{4}x^2+\dfrac{7}{2}x-\dfrac{3}{2}\)
The distribution of pairs of shoes for some
teenagers' closets is as follows.
Pairs of Shoes 1 2 3 4
Frequency
5
18 30 57 30 15
Find the probability a teenager has exactly
4 pairs of shoes in their closet.
P(4) = [?]
Answers
The probability that a teenager has exactly 4 pairs of shoes in their closet is given as follows:
P(4) = 1/5 = 0.2 = 20%.
How to calculate a probability?The parameters that are needed to calculate a probability are given as follows:
Number of desired outcomes in the context of a problem/experiment.Number of total outcomes in the context of a problem/experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes.
The total number of outcomes in this problem is given as follows:
18 + 30 + 57 + 30 + 15 = 150.
30 of the students have exactly 4 pairs, hence the probability is given as follows:
P(4) = 30/150
P(4) = 1/5 = 0.2 = 20%.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1
Someone please answer these 4 mathematical questions please

Answers
Answer:
(5): Missing side: x = 13.9
(6): Missing side: x = 8.5
(7): Measure of indicated angle: ? = 46°
(8): Measure of indicated angle: ? = 35°
Step-by-step explanation:
Because all four triangles are right triangles, we're able to find the side lengths and angles using trigonometry.
(5): When the 44° is the reference angle:
The side that is 10 units long is the adjacent side, and the side that is x units long is the hypotenuse (side always opposite the right angle).Thus, we can find x using the cosine ratio, which is given by:
cos (θ) = adjacent / hypotenuse, where
θ is the measure of the reference angle.Thus, we plug in 44 for θ, 10 for the adjacent side, and x for the hypotenuse and solve for x:
(cos (44) = 10 / x) * x
(x * cos (44) = 10) / cos (44)
x = 13.90163591
x = 13.9
Thus, x is about 13.9 units.
(6): When the 23° angle is the reference angle:
The side that is x units long is the opposite side,and the side that is 20 units long is the adjacent side.Thus, we can find x using the tangent ratio, which is given by:
tan (θ) = opposite / adjacent, where
θ is the reference angle.Thus, we plug in 23 for θ, x for the opposite side, and 20 for the adjacent side and solve for x:
(tan (23) = x / 20) * 20
8.489496324 = x
8.5 = x
Thus, x is about 8.5 units.
Since problems (7) and (8) require to find angles in a right triangle, we will need to use inverse trigonometry.
(7): When the unknown (?) angle is the reference angle:
the side that is 25 units long is the opposite side, and the side that is 35 units long is the hypotenuse.Thus, we can find the measure of the unknown (?) angle in ° using the inverse sine ratio which is given by:
sin^-1 (opposite / hypotenuse) = θ, where
θ reference angleThus, we plug in 25 for the opposite side and 35 for the hypotenuse to solve for θ, the measure of the unknown angle:
sin^-1 (25 / 35) = θ
sin^-1 (5/7) = θ
45.5846914 = θ
46 = θ
Thus, the unknown angle is about 46°.
(8): When the unknown (?) angle is the reference angle:
the side that is 23 units long is the adjacent side, and the side that is 28 units long is the hypotenuse.Thus, we can find the measure of the unknown (?) angle in ° using the inverse cosine ratio which is given by:
cos^-1 (adjacent / hypotenuse) = θ, where
θ reference angleThus, we plug in 23 for the adjacent side and 28 for the hypotenuse to solve for θ, the measure of the unknown angle:
cos^-1 (23 / 28) = θ
34.77194403 = θ
35 = θ
Thus, the measure of the unknown angle is about 35°.
Builtrite is considering purchasing a new machine that would cost $90,000 and the machine would be depreciated (straight line) down to $0 over its five-year life. At the end of five years, it is believed that the machine could be sold for $25,000. The current machine being used was purchased 3 years ago at a cost of $60,000 and it is being depreciated down to zero over its 5-year life. The current machine's salvage value now is $36,000. Also, a higher level of inventory would be needed in the amount of $3000 for the new machine. The new machine would increase EBDT by $56,000 annually. Builtrite’s marginal tax rate is 34%.
What is the TCF associated with the purchase of this machine?
Answers
The TCF associated with the purchase of this machine is -$32,000, indicating a net cash outflow of $32,000 over the 5-year period.
We need to take into account the initial cost, depreciation, salvage value, inventory increase, and the effect on earnings before depreciation and taxes (EBDT) when calculating the Total Cash Flow (TCF) associated with the purchase of the new machine.
Information provided:
New machine cost: $90,000
Deterioration period: 5 years
Assessed rescue worth of new machine following 5 years: Cost of the current machine: $25,000 $60,000
Deterioration time of current machine: Current machine's salvage value in five years: $36,000 More of the new machine's stock: $3,000
Expanded EBDT yearly because of new machine: The marginal tax rate is $56,000. 34 percent Now let's figure out the TCF:
Ascertain the devaluation cost for the two machines:
Depreciation costs for the new machine are as follows: (Cost - Salvage value) / Life; depreciation costs for the current machine are as follows: (Cost - Salvage value) / Life; depreciation costs for the new machine are as follows: (90,000 - $25,000) / 5 = $13,000; depreciation costs for the current machine are as follows: (60,000 - $36,000) / 5 = $4,800.
The annual increase in earnings before depreciation and taxes (EBDT) can be calculated by multiplying the tax savings for the new machine by the depreciation expense, multiplied by the tax rate, and the tax savings for the current machine by the depreciation expense, multiplied by the tax rate.
The net cash inflow resulting from the increased EBDT can be calculated as follows: EBDT increase = Increased EBDT - Tax savings for the current machine EBDT increase = $56,000 - $1,632 = $54,368
The net cash inflow is equal to the EBDT increase minus the tax rate. The net cash inflow is equal to $35,899.52 minus the 0.34 percent figure.
Absolute money surge = Cost of new machine + Expanded stock
Absolute money surge = $90,000 + $3,000 = $93,000
Compute the rescue worth of the ongoing machine toward the finish of its 5-year life:
The machine's salvage value is $36,000. At the end of five years, the total cash inflow will be as follows:
All out cash inflow = Rescue worth of new machine + Rescue worth of current machine
All out cash inflow = $25,000 + $36,000 = $61,000
Ascertain the TCF:
The TCF associated with the purchase of this machine is -$32,000, indicating a net cash outflow of $32,000 over the course of the five years. TCF = Total cash inflow - Total cash outflow TCF = $61,000 - $93,000 = -$32,000
To know more about Cash Flow refer to
https://brainly.com/question/30066211
#SPJ11
What would be the angle between the two perpendicular lines.
Answers
Answer:
90 degrees
90 degreesPerpendicular lines are lines that intersect at a right (90 degrees) angle.
Suppose 60% of the graduating class in a certain high school goes to college. If 240 students from this graduating class are going to college, how many students are in the class?
Answers
Answer:
400 students
Step-by-step explanation:
We can rewrite the problem using the words is and of:
240 is 60% of the total number of students in the graduating class.
A simple formula for percentage problems is Px = y, where P is the percentage.
In this case, we only know that 240 is 60% of some number, so we must find x:
\(0.60x=240\\x=400\)
Find the product. Simplify your answer. (3f–1)(4f+1)
Answers
Explanation: just did it on get more math and i was right
PLEASE HELP WITH THIS!!!!!

Answers
Consider F and C below.
F(x, y, z) = yz i + xz j + (xy + 14z) k
C is the line segment from (3, 0, −1) to (6, 4, 2)
(a) Find a function f such that F = ∇f.
f(x, y, z) =
(b) Use part (a) to evaluate
C
∇f · dr along the given curve C.
Answers
∇f · dr = (3/2)(0) + (4)(0) + (3)(0) = 0
Therefore, C∇f · dr along the given curve C is 0.
Consider F and C below.
F(x, y, z) = yz i + xz j + (xy + 14z) kC is the line segment from (3, 0, −1) to (6, 4, 2)
(a) Find a function f such that F = ∇f.f(x, y, z) = x y z + 7 z2
(b) Use part (a) to evaluate C∇f · dr along the given curve C.(a) Given F(x, y, z) = yz i + xz j + (xy + 14z) k, we need to find a function f such that F = ∇f.
Let F = ∇f
Then ∂f/∂x = yz, ∂f/∂y = xz and ∂f/∂z = xy + 14z
∴ Integrating ∂f/∂x = yz w.r.t x,
we get f = xyz + g(y, z).
Here, g(y, z) is an arbitrary function of y and z.
Differentiating f w.r.t y and equating it to xz, we get
∂f/∂y = xz + ∂g/∂y
∴ Integrating ∂g/∂y = 0 w.r.t y, we get g(y, z) = h(z).
Here, h(z) is an arbitrary function of z.
Thus, we get f(x, y, z) = xyz + h(z).
Differentiating f w.r.t z and equating it to xy + 14z, we get
∂f/∂z = xy + 14z
∴ f = x y z + 7 z2
Thus, f(x, y, z) = x y z + 7 z2
(b) Now, we need to evaluate C∇f · dr along the given curve C.Curve C is the line segment from (3, 0, −1) to (6, 4, 2).
Let C(t) be a parametrization of the curve C, where C(0) = (3, 0, −1) and C(1) = (6, 4, 2)
Given that f(x, y, z) = x y z + 7 z2
Thus, ∇f(x, y, z) = yz i + xz j + (2xy + 14z) k
At the point (3, 0, −1), we have ∇f(3, 0, −1) = 0 i + 0 j + 0 k = 0
Similarly, at the point (6, 4, 2), we have ∇f(6, 4, 2) = 32 i + 24 j + 64 k
Now, dr = C′(t) dt = (dx/dt) i + (dy/dt) j + (dz/dt) k dt
⇒ dr = 3/2 i + 4 j + 3 k dt along the given curve C.
Then, ∇f · dr = (3/2)(0) + (4)(0) + (3)(0) = 0
Therefore, C∇f · dr along the given curve C is 0.
To know more about curve visit:
https://brainly.com/question/32496411
#SPJ11
Question 2 of 13
Which of the following quadratic regression equations best fits the data
shown below?

Answers
Answer:
I'm gonna go with b to be honest sorry if I'm wrong
HELP ASAP!!!!!! Please answer both:)


Answers
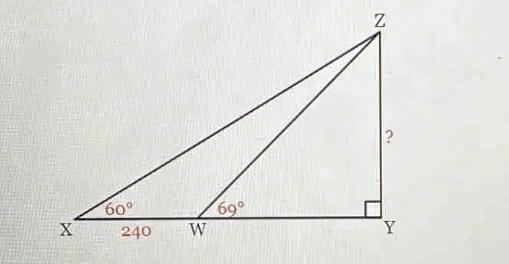
In ΔXYZ, ∠Y=90° and ∠X=60°. ∠ZWY=69° and XW=240. Find the length of ZY to the nearest 10th.
Answers
The value of length ZY in nearest 10th place is 1,240.8 units.
What is the value of length ZY?The value of length ZY is calculated as follows;
Considering triangle XYZ;
tan 60 = ZY/XY
let length WY in triangle WYZ = ntan 60 = (ZY)/(240 + n)
ZY = 1.732(240 + n) ------ (1)
Considering triangle WYZ;
tan 69 = ZY/WY
tan 69 = ZY/n
n = ZY/tan69
n = 0.384(ZY) ---------- (2)
The length ZY is calculated as;
Substitute the value of n into equation (1)
ZY = 1.732(240 + 0.384ZY)
ZY = 415.68 + 0.665ZY
0.335ZY = 415.68
ZY = 415.68 / 0.335
ZY = 1,240.8 units
From equation (2);
n = WY = 0.384 (1,240.8)
WY = 476.5 units
Learn more about length of triangle here: https://brainly.com/question/24597672
#SPJ1
Plot the frequency response and the impulse response of the LTI system having the output y = 2te-ul for the input x) = -(t).
Answers
Given an LTI system that has an output y = 2te^-ul for the input x(t) = -(t). Here, e^-ul is the decay constant and is a real positive constant. The impulse response of the system can be found by considering the impulse input x(t) = δ(t).
The output of the system with an impulse input is given by y(t) = h(t), where h(t) is the impulse response of the system.We have,x(t) = -(t)..........(1)Applying derivative on both sides of the above equation, we get,y(t) = 2te^-ul, Applying derivative on both sides of the above equation, we get,
Plot of frequency response and Impulse response of the system Hence, the plot of frequency response and the impulse response of the LTI system is shown in the figure below:, the frequency response is given by H(jω) = (2/(-jω + ul)^2) where ω is the angular frequency. The impulse response of the system is given by h(t) = (2/ul^2)t.e^-ul.
To know more about system visit:
https://brainly.com/question/19843453
#SPJ11
n < -4
need answers fast math test to at 11:59 pm today but gotta get done faster than that.
plz. and thank you!!
Answers
Plz mark Brainliest
Answer:
N would equal anything lower than -4 for example, -5 or -6
Step-by-step explanation:
yw
What’s the slope of the line ? (4.5), (6,2)
Answers
Answer:
This is a negative slope.
Step-by-step explanation:
When plotting the numbers on a graph, the slope goes downhill from left to right.
Answer:
In the pic
Step-by-step explanation:
If you have any questions about the way I solved it, don't hesitate to ask me in the comments below ;)

Read the following excerpt from a magazine carefully, and complete the activities.
In Arizona, spring is the most beautiful time of year. The temperature usually ranges from sixty-five to ninety degrees Fahrenheit. Statistics show that the sun shines 89 percent of the time during the spring days.
Birds love Arizona in the spring. Children laugh and play, and families get together for picnics. Thousands of people like to go to the lake to water ski or swim, while others enjoy driving to the forest-covered mountains to camp and fish.
List at least one statement from each of the two paragraphs that is an opinion rather than a provable fact.
first paragraph:
second paragraph:
first paragraph: second paragraph:
Answers
Paragraph 1: Spring is the most beautiful time of the year - the Authors opinion and not fact.
Paragraph 2: Birds love the spring - Nobody knows how a bird is feeling, this is just based off of the Author trying to make a scenery for you.
Hoped this helped :)
Find the value of x such that the area of a triangle whose vertices have coordinates (6, 5), (8, 2) and (x, 11) is 15 square units.
Answers
Answer:
\(x =12\ or\ -8\)
Step-by-step explanation:
Given
\((x_1,y_1) = (6,5)\)
\((x_2,y_2) = (8,2)\)
\((x_3,y_3) = (x,11)\)
\(Area = 15\)
Required
Find x
The area is calculated as thus:
\(Area = \frac{1}{2}|x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|\)
Substitute values
\(15 = \frac{1}{2}|6*(2 - 11) + 8*(11 - 5) + x(5 - 2)|\)
\(15 = \frac{1}{2}|6*(-9) + 8*(6) + x(3)|\)
\(15 = \frac{1}{2}|-54 + 48 + 3x|\)
\(15 = \frac{1}{2}|-6 + 3x|\)
Multiply through by 2
\(2 * 15 = \frac{1}{2}|-6 + 3x| * 2\)
\(30 = |-6 + 3x|\)
Remove absolute sign
\(30 = -6 + 3x\ or\ -30 = -6 + 3x\)
Add 6 to both sides
\(36 = 3x\ or\ -24 = 3x\)
Divide by 3
\(12 = x\ or\ -8 = x\)
\(x =12\ or\ -8\)
So, the coordinates are (-8, 11) or (12,11)
What is the answer to

Answers
Answer:
I think the answer will be 18
Chris P. Bacon owns 13 animals. Some are chickens and some are pigs. There are 40 legs in all. How many of each animal does Chris own?
it would be helpful to get the system for the equation as well.
Answers
There are 7 pigs and 6 chickens. Pigs have 4 legs while chickens only have two.
Calculate the effective interest on £2000 at 3% interest
quarterly after 4 years.
Answers
The effective interest on £2000 at a 3% interest rate compounded quarterly over a period of 4 years is approximately £245.15.
To calculate the effective interest, we need to use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A = the future value of the investment (including interest)
P = the principal amount (initial investment)
r = the annual interest rate (as a decimal)
n = the number of compounding periods per year
t = the number of years
In this case, the principal amount (P) is £2000, the annual interest rate (r) is 3% (or 0.03 as a decimal), the compounding is done quarterly (n = 4), and the investment period (t) is 4 years.
Plugging the values into the formula:
A = £2000(1 + 0.03/4)^(4*4)
= £2000(1 + 0.0075)^16
= £2000(1.0075)^16
≈ £2000(1.126825)
Calculating the future value:
A ≈ £2253.65
To find the effective interest, we subtract the principal amount from the future value:
Effective Interest = £2253.65 - £2000
≈ £253.65
Therefore, the effective interest on £2000 at a 3% interest rate compounded quarterly after 4 years is approximately £253.65.
Learn more about compound interest here:
https://brainly.com/question/22621039
#SPJ11
Find g[f(-2)], if f(x) = x^2 and g(x) = 3x – 5.
A. -17
B. -7
C. 7
D. -44
Answers
Answer:
g[f(-2)] = 7
Step-by-step explanation:
f(x) = x^2
g(x) = 3x – 5
g[f(-2)]
First find f(-2) = (-2)^2 = 4
Then find g(4) = 3(3) -5 = 12-5 = 7
\(f(x)=x^2;g(x)=3x-5\\\\g[f(-2)]=3\times (f(-2))^2-5=3\times(-2)^2-5=3\times4-5=7\)
Answer: c
hope it helps
The relationship between hours practice and coordinate video game is modeled by the equation Y = 10x graph this relationship on the graph below what is the slope and what does it mean for the situation
Answers
answer:
provided in the explanation.
step-by-step explanation:
the graph would contain the points (0,0), (1,10), (2,20), etc. the slope is 10, which represents the number of coordinate video games practiced in x number of hours. the representation for the slope depends on whether coordinate video game or hours practiced is on the x or y axis. hope that helps!
Consider the function f(x) = x2 - 4x + 8 on the interval 0, 4. Verify that this function satisfies the three hypotheses of Rolle's Theorem on the inverval f(x) is f(x) is and f(0) on [0, 4] on (0, 4) f(4) Then by Rolle's theorem, there exists at least one value c such that f'(c) = 0. Find all such values c and enter them as a comma-separated list. Values of c =: (1 point) Consider the function graphed below. P n ? Does this function satisfy the hypotheses of the Mean Value Theorem on the interval a, b ? Does it satisfy the conclusion?? f(b) f(a)2 At what point c is f'(c) b - a
Answers
Verifying that this function satisfies the three hypotheses of Rolle's Theorem on the inverval f(x) is f(x) is and f(0) on [0, 4] on (0, 4) f(4) Then by Rolle's theorem, there exists at least one value c = 2 such that f'(c) = 0.
Given:
Consider the function f(x) = x2 - 4x + 8 on the interval 0, 4. Verify that this function satisfies the three hypotheses of Rolle's Theorem on the inverval f(x) is f(x) is and f(0) on [0, 4] on (0, 4) f(4) Then by Rolle's theorem, there exists at least one value c such that f'(c) = 0.
f(x)=x^2−4x+8, [0,4]
when, x = 0
f(x) = x^2 -4x +8
f(0) = y = 0 - 0 + 8 = 8
when, x=4
f(5) = y = 16 - 16+8 =
thus, we have 2 points (0, 8) ; (4, 8)
slope,m = {8-(8)} / {4-0} = 0
hence, we have to calculate all the points,x where 0<x<8 and slope=0
f '(x) = 2x - 4 = 0
or, f '(c) = 2c - 4 = 0
c = 4/2 =2 ( 0<x<4)
hence, the there is only one solution c=2 which satisfies Rolle's theorem.
Learn more about the rolle's theorem here:
https://brainly.com/question/13972986
#SPJ4
Find the slope of a line with these two points:
(3, 4) and (-1, 2)
a. -1/2
b. -1/3
c. 1/2
d. 3/4

Answers
Answer: C
Step-by-step explanation:
slope = (y2 - y1) / (x2 - x1)
= (2 - 4) / (-1 - 3)
= -2 / -4
= 1/2
When constructing a confidence interval for the population mean using the standard deviation of the sample, the degrees of freedom for the t distribution equals
a n.
b n - 1.
c 2n.
d n + 1.
Answers
The answer is b) n - 1. When constructing a confidence interval for the population mean using the standard deviation of the sample, we use the t-distribution.
The degrees of freedom for the t-distribution is given by n - 1, where n is the sample size. This is because we estimate the population mean using the sample mean, and we lose one degree of freedom in the process. Degrees of freedom refer to the number of independent pieces of information available for estimating a parameter.
Since one piece of information is used to estimate the sample mean, we subtract one from the sample size to get the degrees of freedom for the t-distribution. Therefore, the correct option is b) n - 1.
Learn more about Standard Deviation:
https://brainly.com/question/24298037
#SPJ4
factor the trinomial below. x^2+13x+42
Answers
Answer:
(x + 6)(x + 7)
Step-by-step explanation:
To factor the trinomial x^2 + 13x + 42, we need to find two numbers that multiply to 42 and add up to 13.
One way to do this is to list all the pairs of factors of 42 and see which pair adds up to 13:
1, 42 -> 1 + 42 = 43
2, 21 -> 2 + 21 = 23
3, 14 -> 3 + 14 = 17
6, 7 -> 6 + 7 = 13
So the pair of factors that we want is 6 and 7. We can use these numbers to rewrite the middle term of the trinomial:
x^2 + 13x + 42 = x^2 + 6x + 7x + 42
Next, we can group the first two terms and the last two terms:
x^2 + 6x + 7x + 42 = (x^2 + 6x) + (7x + 42)
Now, we can factor out the greatest common factor from each group:
x(x + 6) + 7(x + 6)
Notice that we have a common factor of (x + 6) in both terms. We can factor this out:
(x + 6)(x + 7)
suppose that grade point averages of undergraduate students at one university have a bell-shaped distribution with a mean of 2.61 and a standard deviation of 0.41 . using the empirical rule, what percentage of the students have grade point averages that are between 1.38 and 3.84 ?
Answers
By empirical rule, 99.7% of the students have a grade point average which is between 1.38 and 3.84.
Suppose that the grade point average of undergraduate students at one university has a bell-shaped distribution with a mean of 2.61 and a standard deviation of 0.41.
Here, μ = 2.61 , σ = 0.41
Using the empirical rule :
The first part of the empirical rule states that 68% of the data values will fall within 1 standard deviation of the mean. To calculate "within 1 standard deviation," you need to subtract 1 standard deviation from the mean, then add 1 standard deviation to the mean. That will give you the range for 68% of the data values.
2.61 − 0.41 = 2.2
2.61 + 0.41 = 3.02
The range of numbers is 2.2 to 3.02
The second part of the empirical rule states that 95% of the data values will fall within 2 standard deviations of the mean. To calculate "within 2 standard deviations," you need to subtract 2 standard deviations from the mean, then add 2 standard deviations to the mean. That will give you the range for 95% of the data values.
2.61 − 2(0.41) = 1.79
2.61 + 2(0.41) = 3.43
The range of numbers is 1.79 to 3.43
Finally, the last part of the empirical rule states that 99.7% of the data values will fall within 3 standard deviations of the mean. To calculate "within 3 standard deviations," you need to subtract 3 standard deviations from the mean, then add 3 standard deviations to the mean. That will give you the range for 99.7% of the data values.
2.61 − 3(0.41) = 1.38
2.61+3(0.41) = 3.84
The range of numbers is 1.38 to 3.84.
Hence, 99.7% of the students have a grade point average which is between 1.38 and 3.84.
To learn more about empirical rules here:
brainly.com/question/30404590
#SPJ4