5. How much interest will you pay for a $198.000 mortgage if you finance the home
for 30 years at 4% interest (Use a mortgage calculator)
$1, 141
Answers
The total amount of interest you would pay for a $198,000 mortgage over a 30-year term at a 4% interest rate is approximately $143,739.
This means that the total amount you would end up paying for your home would be $341,739 (including the principal loan amount of $198,000 plus the interest).
This is assuming that the interest rate remains the same for the entire 30-year term and that there are no additional fees or charges associated with the mortgage. Of course, there are many factors that could impact your total interest and mortgage payments '
so it's important to work closely with a mortgage lender or financial advisor to understand your specific situation and options.
To know more about interest visit:-
https://brainly.com/question/31907854
#SPJ11
Related Questions
Question 8 of 10
Which of the diagrams below represents the statement "If it is an triangle,
then it has three vertices"?
three
vertices
triangle
triangle
three
vertices
Figure A
Figure B
A. Figure A
B. Figure B

Answers
A recording company obtains the blank cds used to produce its labels from three compact disk manufacturers: i, ii, and iii. The quality control department of the company has determined that 3% of the compact disks produced by manufacturer i are defective, 4% of those produced by manufacturer ii are defective, and 2% of those produced by manufacturer iii are defective. Manufacturers i, ii, and iii supply 36%, 52%, and 12%, respectively, of the compact disks used by the company. What is the probability that a randomly selected label produced by the company will contain a defective compact disk?.
Answers
The probability that a randomly selected label produced by the company will contain a defective compact disk is 0.034.
How to calculate the probability?In this, it should be noted that there are 3 possible cases in the chosen disc can be from any of the manufacturing companies, so the total probability will be the sum of probabilities of getting a faulty disc from companies 1-3.
The probability from company 1 will be;
= 0.03*0.36
The probability from company 2 will be:
= 0.04*0.52
The probability from company 3 will be:
= 0.02*0.12
The total probability will now be:= (0.36*0.03)+(0.04*0.52)+(0.02*0.12)
= 0.0108 + 0.0208 + 0.0024
= 0.034
Learn more about probability on:
https://brainly.com/question/24756209
#SPJ1
What is the slope of a line perpendicular to a line with slope -6/5? *
-6/5
-5/6
5/6
-4/3
Answers
Answer:
5/6
Step-by-step explanation:
The slope of a perpendicular line is the negative reciprocal of the other.
Given: m = -6/5
Negative: m = 6/5
Reciprocal: m = 5/6
y equals the quotient of the quantity x squared plus 4 times x and the quantity x cubed minus 5.
Answers
Given:
Consider the completer question is "Find the derivative \(\dfrac{dy}{dx}\) for \(y=\dfrac{x^2-4x}{x^3-5}\)."
To find:
The derivative \(\dfrac{dy}{dx}\).
Solution:
Chain rule: \(\dfrac{d}{dx}f(g(x))=f'(g(x))\cdot g'(x)\)
Quotient rule: \(\dfrac{d}{dx}\dfrac{f(x)}{g(x)}=\dfrac{g(x)f'(x)-f(x)g'(x)}{[g(x)]^2}\)
We have,
\(y=\dfrac{x^2-4x}{x^3-5}\)
Differentiate with respect to x.
\(\dfrac{dy}{dx}=\dfrac{d}{dx}\left(\dfrac{x^2-4x}{x^3-5}\right)\)
Using chain rule and quotient rule, we get
\(\dfrac{dy}{dx}=\dfrac{(x^3-5)\dfrac{d}{dx}(x^2-4x)-(x^2-4x)\dfrac{d}{dx}(x^3-5)}{(x^3-5)^2}\)
\(\dfrac{dy}{dx}=\dfrac{(x^3-5)(2x-4)-(x^2-4x)(3x^2)}{(x^3-5)^2}\)
\(\dfrac{dy}{dx}=\dfrac{2x^4-4x^3-10x+20-3x^4+12x^3}{(x^3-5)^2}\)
\(\dfrac{dy}{dx}=\dfrac{-x^4+8x^3-10x+20}{(x^3-5)^2}\)
Therefore, the required answer is \(\dfrac{dy}{dx}=\dfrac{-x^4+8x^3-10x+20}{(x^3-5)^2}\).
Orange County wanted to determine how its students did on a standardized test, so the county took a random survey of 25 students. Out of the 25 students, 4 scored "1" on the test, 8 scored "2" on the test, 5 scored "3" on the test, 5 scored "4" on the test, and 3 scored "5" on the test.
Answers
The model could be improved by using a step function.
what does it mean when we say that the tails of the normal curve are asymptotic to the x axis? multiple choice the tails get closer and closer to the x axis but never touch it. the tails get closer and closer to the x axis and eventually touch it. the tails get closer and closer to the x axis and eventually cross this axis. the tails get closer and closer to the x axis and eventually become this axis.
Answers
When we say that the tails of the normal curve are asymptotic to the x axis, it mean the tails get closer and closer to the x axis but never touch it
The tails of normal curve are actually asymptotic. To say they are asymptotic, then it means that they approach the x axis but never quite meet its horizons.
These tails will extends indefinitely in both directions without crossing and touching the x axis or the horizontal axis.
Tails of normal curve or normal curve itself is asymptotic to the x-axis. That is the curve touches the x-axis only at -∞ and +∞. So the curve only approaches nearer and nearer to x-axis but never touches or crosses it.
For this reason, the correct choice is get closer and closer to the x-axis but never touches it.
Learn more about normal curves here:
https://brainly.com/question/23418254
#SPJ4
Tricia starts school at 7:00 AM and has lunch at 12:00 PM. She wants to make sure she has something to eat in between. Determine what time she should eat her snack if she is to eat at exactly a time between starting school and eating lunch. (Hint: Set up a horizontal number line as a timeline.) A. A. 9:30 AM
B. 10:00 AM
C. 9:00 AM
D. 10:30 AM
Answers
Answer:
D) 9:00 am
Step-by-step explanation:
Because 9:00 is the midpoint of 7 and 12
Suppose I randomly choose 4 distinct integers between 1 and 60. Is it true, or is it not true, that at least 2 of them must differ by no more than 19.
Answers
Answer:
It’s true
Step-by-step explanation:
Proof by induction
Let the four chosen numbers be x_1, … x_4 and, without loss of generality, let x_1 < x_2, … < x_4.
For x_1 = 1, the smallest possible choice, let x_2 = x_1 + 20 = 21 be the smallest possible choice that has a difference larger than 19. Likewise, x_3 = x_2 + 20 = x_1 + 40 = 41. Then x_4 has to be at least x_3 + 20 = x_1 + 60 = 61 which is out of range.
For the induction, suppose that x_4(n) = x_1(n) + 60 > 60 and therefore x_4(n) can’t be chosen for a given x_1(n). Then incrementing x_1(n+1) = x_1(n) + 1 would require x_4(n+1) to be at least x_1(n) + 1 + 60 = x_4(n) + 1 > 61, so this is out of range as well.
For another induction, suppose that x_4(n) = x_2(n) + 40 > 60 and therefore x_4(n) can’t be chosen for a given x_2(n). Then incrementing x_2(n+1) = x_2(n) + 1 would require x_4(n+1) to be at least x_2(n+1) + 40 = x_4(n) + 1 > 61, so this is out of range as well.
Likewise, for the induction, suppose that x_4(n) = x_3(n) + 20 > 60 and therefore x_4(n) can’t be chosen for a given x_3(n). Then incrementing x_3(n+1) = x_3(n) + 1 would require x_4(n+1) to be at least x_3(n+1) + 20 = x_4(n) + 1 > 61, so this is out of range as well.
Therefore all choices of x_1, x_2, x_3 with differences greater than 19 leaves no choice of x_4 within range with x_4 > x_3 + 19.
in a manufacturing process, a random sample of 36 manufactured bolts has a mean length of 3 inches with a standard deviation of .3 inches. what is the 99 percent confidence interval for the true mean length of the manufactured bolt?
Answers
The 99% confidence interval for the true mean length of the manufactured bolt is (2.9177, 3.0823)
Here, we need to construct a 99% confidence interval for population mean (μ) is given by
μ = x + Zα/2 * σ/√n or μ = x - Zα/2 * σ/√n
where, μ = population mean
x = sample mean
= 3 inches
σ = population standard deviation
= 0.3 inches
Zα/2= z score for a two tailed test at level of significance α = 2.576( for a 99% confidence level)
So, the upper limit would be,
μ = 3 + 1.645 * (0.3/√36)
μ = 3 + 1.646 * (0.3/6)
μ = 3.0823
And the lower limit would be,
μ = 3 - 1.645 * (0.3/√36)
μ = 3 - 1.646 * (0.3/6)
μ = 2.9177
Hence, the 99% confidence interval is (2.9177, 3.0823)
Learn more about confidence interval here:
https://brainly.com/question/24131141
#SPJ4
help how do i prove the two triangles are congruent
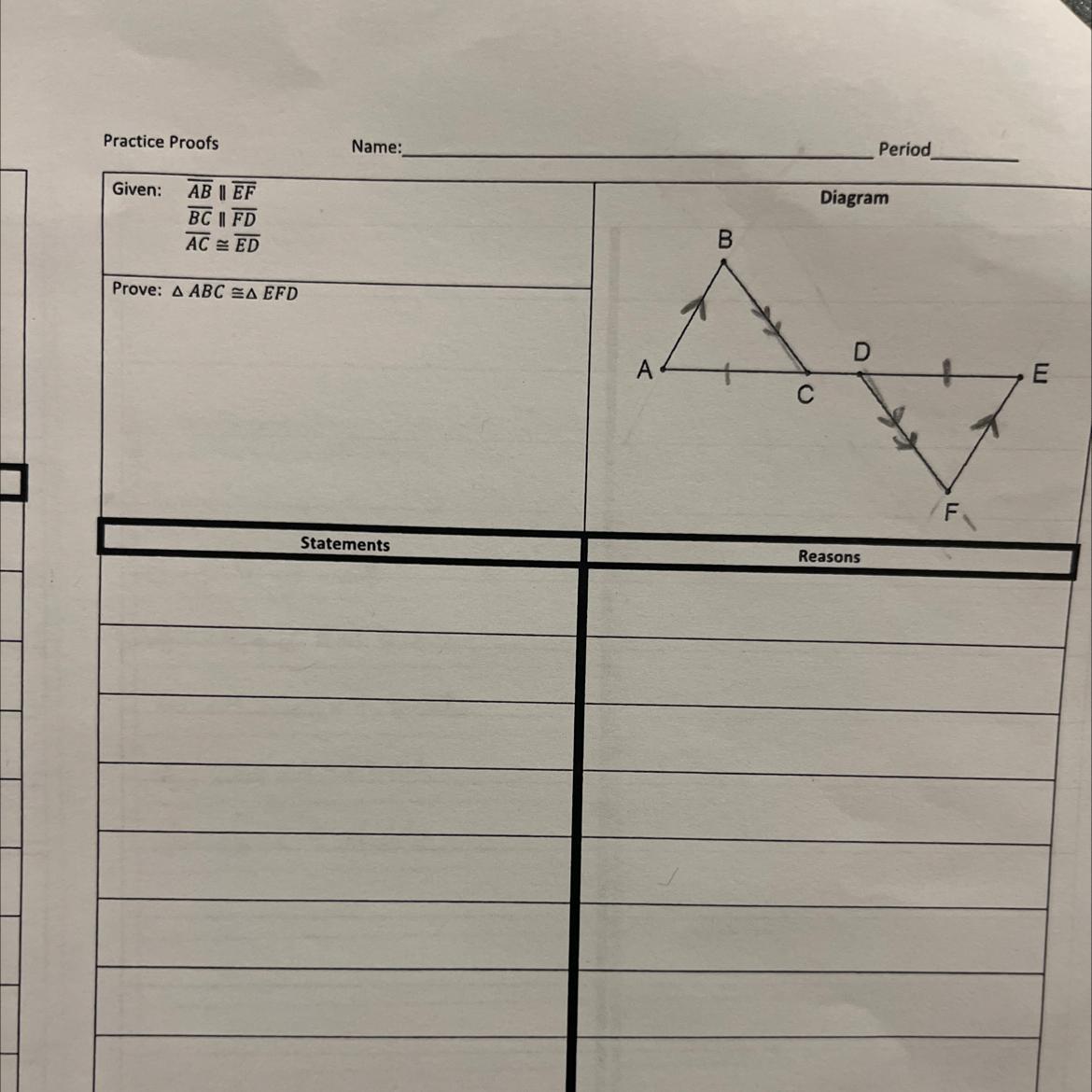
Answers
Explanation:each side or angle should have a symbol and if the two triangles share the same symbols then they are congruent
Does 4 8 and 12 make a triangle?
Answers
No, 4, 8, and 12 are not valid side lengths for a triangle. So 4, 8 and 12 does not make a triangle.
In order for a shape to be a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. This is known as the triangle inequality theorem.
If a triangle has sides of length 4, 8, and 12, then the triangle inequality theorem would be:
8 + 12 > 4 (true, as 8+12 =20)
12 + 4 > 8 (true, as 4+12=16)
4 + 8 > 12 (false, as 4+8 =12)
Since 4 + 8 = 12, and 12 is not greater than 4 or 8, a triangle cannot be formed with sides of length 4, 8, and 12.
To know more on triangle inequality theorem
https://brainly.com/question/1163433
#SPJ4
Plz Help!!! I really do not get this lesson and I really need to pass it to move onto the next I am kind of getting it, I want to make sure my answer is correct. IS it sas?

Answers
Answer:
SSS
Step-by-step explanation:
I think it would be SSS (side, side, side)... let me know if I'm wrong and I'll try again:)
Check out the diagram below. I've marked the angles and sides that are congruent. Notice how the marked sides are not between the marked angles for either triangle. So we're dealing with AAS instead of ASA. The order is important. If we wanted to use ASA, then we would have to know DE = TU, both of those sides are between the marked angles.

Find a vector parallel to the line of intersection of the planes given by the equations 2x - 3y + 5z = 2 and 4x + y - 3z = 7
Answers
The vector <-32, 44, 22> is parallel to the line of intersection of the two planes given by the equations 2x - 3y + 5z = 2 and 4x + y - 3z = 7.
To find a vector parallel to the line of intersection of the planes given by the equations 2x - 3y + 5z = 2 and 4x + y - 3z = 7, we first need to find the direction vector of the line of intersection.
We can find the direction vector by taking the cross product of the normal vectors of the two planes. The normal vector of the plane 2x - 3y + 5z = 2 is <2, -3, 5>, and the normal vector of the plane 4x + y - 3z = 7 is <4, 1, -3>. Taking the cross product of these two vectors, we get:
<2, -3, 5> × <4, 1, -3> = <-16, 22, 11>
This vector <-16, 22, 11> is the direction vector of the line of intersection of the two planes.
To find a vector parallel to this line, we can simply multiply the direction vector by a scalar. For example, we can choose a scalar of 2 to get:
2<-16, 22, 11> = <-32, 44, 22>
Therefore, the vector <-32, 44, 22> is parallel to the line of intersection of the two planes given by the equations 2x - 3y + 5z = 2 and 4x + y - 3z = 7.
Learn more about line of intersection here
https://brainly.com/question/31743634
#SPJ11
Sasha sells T-shirts. Each day she earns a set amount, plus a commission. Choose the linear function f to determine Sasha's pay.
f(x) = 68x + 3
f(x) = 3x + 65
f(x) = 3x + 68
f(x) = x + 68
Answers
Answer:
a. The correct option is f(x) = 3x + 65.
b. Sasha earns 146 that day.
Step-by-step explanation:
Note: This question is not complete. The complete question is therefore provided before answering the question. See the attached pdf file for the complete question.
The explanation to the answer is now given as follows:
a. Choose the linear function f to determine Sasha's pay.
Note: See the attached excel file to see the determination of the correct linear function f to determine Sasha's pay.
From the list of linear functions f given in the question, x represents the number of T-shirts Sasha sold in one day.
Therefore, the correct linear function f to determine Sasha's pay can be determined by simply substituting number of T-shirts for x in each of the linear function f to see which one is the same as the table provided in the question.
From the attached excel file, the correct option is f(x) = 3x + 65. This is indicated in bold red color in the attached excel file.
b. If Sasha sells 27 T-shirts in one day how much money does she earn that day?
This can be calculated using f(x) = 3x + 65 which is the correct linear function f determined in part a above and substituting 27 for x as follows:
Sasha’s earning = 3(27) + 65
Sasha’s earning = (3 * 27) + 65
Sasha’s earning = 81 + 65
Sasha’s earning = 146
Therefore, Sasha earns 146 that day.
Answer:
f(x) = 3x + 65
Step-by-step explanation:
A variable resistor R and an 8-Ω resistor in parallel have a combined resistance RT given by RT =8R/(8+R) . If R is changing at 0.30 /min, find the rate at which R, is changing when R = 6.0 Ω
Create a report on the application you selected. Include the problem statement, mathematical and verbal work to answer all parts of the problem, and additional discussion of the problem and how it is useful. Note, you are to not only answer the question posed in the textbook, you are to create and comment on the application in general.
Your write-up should include proper mathematical notation and justification for all work and answers, both mathematical and verbal, along with a citation of the textbook since you will be using a problem from the book in your work.
Answers
In this problem, we are given a variable resistor R and an 8-Ω resistor in parallel. We are asked to find the rate at which the resistance R is changing when it is equal to 6.0 Ω.
Given that RT = 8R / (8 + R), we can differentiate this equation with respect to time t using the quotient rule. Let's denote dR/dt as the rate of change of R with respect to time. Applying the quotient rule, we have:
dRT/dt = \([ (8)(dR/dt)(8 + R) - (8R)(dR/dt) ] / (8 + R)^2\)
To find the rate at which R is changing when R = 6.0 Ω, we substitute R = 6.0 into the above equation:
dRT/dt = \([ (8)(dR/dt)(8 + 6.0) - (8)(6.0)(dR/dt) ] / (8 + 6.0)^2\)
Simplifying further, we have:
dRT/dt = \([ (8)(dR/dt)(14) - (48)(dR/dt) ] / (14)^2\)
dRT/dt = (112(dR/dt) - 48(dR/dt)) / 196
dRT/dt = 64(dR/dt) / 196
dRT/dt = 16(dR/dt) / 49
Therefore, the rate at which R is changing when R = 6.0 Ω is equal to 16/49 times the rate of change of RT.
Learn more about rate of change here:
https://brainly.com/question/13734552
#SPJ11
Please help giving up 20 points for answers


Answers
Answer:
Question 2: 6x-21
Question 1: -9x+3
Step-by-step explanation:
A bike was reduced by 20% in a sale.
If its sale price was £520, what was its original price?
Answers
Answer:
416
Step-by-step explanation:
Answer:
£500
Step-by-step explanation:
a hippogriff rancher wants to enclose a rectangular area and then divide it into four pens with fencing parallel to one side of the rectangle (see the figure below). he has 590 feet of fencing available to complete the job. what is the largest possible total area of the four pens?
Answers
The largest area is found to be 8702.5 \(ft^{2}\).
We know that area of rectangle
A = xy ........ (1)
Perimeter of rectangle (given) = 590 ft
Using x and y as two variables ;
5x + 2y = 590
solve yb in term of x
y = -5/2 x + 295......(2)
Now we will get area only in one variable from (1) and (2)
A = x ((-5/2)x + 295)
A = -5/2 \(x^{2}\) + 295x
differentiate it with respect gto x
A' = -5x + 295........ (3)
find the critical point to get your minima and maxima value.
Put A' = 0, x = 295/5 = 59
x = 59
then , from (2)
y= (-5/2 × 59) + 295 = 147.5
y = 147.5
again differentiate (3)
A'' = -5 < 0. i.e critical point x = 59 is point of maxima.
So, maximum area = 59 × 147.5
Largest area = 8702.5 \(ft^{2}\)
Learn more about area here ;
https://brainly.com/question/25292087
#SPJ4
is the average (arithmetic mean) of x and y greater than 20?1. the average (arithmetic mean) of 2x and 2y is 48.2. x
Answers
After answering the provided question, we can conclude that the average (arithmetic mean) of 2x and 2y is 48.
What is mean?The mean of a dataset is the sum of all values divided by the total number of values; this is also known as the arithmetic mean (as opposed to the geometric mean). Often referred to as the "mean," this is the most often used measure of central tendency. Simply dividing the total number of values in the dataset by the sum of those values yields this result. Calculations can be performed using both raw data and data that has been combined into frequency tables. The average of a number is referred to as its average. It is simple to calculate: Divide the total number of digits by the number of digits. the total divided by the count.
The average (arithmetic mean) of 2x and 2y is 48.
To know more about the mean visit:
brainly.com/question/30094057
#SPJ4
Generate two ordered pairs by substituting
zero for x and y. Then, find the rate of change.
-3x-6y=-3
Answers
The ordered pairs for the equation is ( 0 , 0.5 ) and ( 1 , 0 )
Given data ,
Let the equation be represented as A
Now , the value of A is
-3x - 6y = -3
To generate two ordered pairs by substituting zero for x and y, we can substitute x = 0 and y = 0 into the given equation -3x - 6y = -3 and solve for y.
For x = 0:
-3(0) - 6y = -3
0 - 6y = -3
-6y = -3
y = -3 / -6
y = 0.5
So the first ordered pair is (0, 0.5)
For y = 0:
-3x - 6(0) = -3
-3x - 0 = -3
-3x = -3
x = -3 / -3
x = 1
So the second ordered pair is (1, 0)
The rate of change is the change in y-coordinate divided by the change in x-coordinate.
In this case, as we move from the first ordered pair (0, 0.5) to the second ordered pair (1, 0), the change in y-coordinate is -0.5 and the change in x-coordinate is 1.
Therefore, the rate of change is -0.5 / 1 = -0.5.
Hence , the ordered pairs are ( 0 , 0.5 ) and ( 1 , 0 )
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
a is an nn matrix. determine whether the statement below is true or false. justify the answer. if a for some scalar , then is an eigenvector of a.
Answers
The statement is false. The existence of a scalar α such that αv is an eigenvector of a does not imply that v itself is an eigenvector of a.
What is matrix?A group of numbers built up in a rectangular array with rows and columns. The elements, or entries, of the matrix are the integers. In addition to numerous mathematical disciplines, matrices find extensive use in the fields of engineering, physics, economics, and statistics.
The statement is false. An eigenvector is a non-zero vector that, when multiplied by a matrix, produces a scalar multiple of itself. In other words, if v is an eigenvector of a matrix A, then Av = λv, where λ is the corresponding eigenvalue.
The statement suggests that if a is an nn matrix (presumably an n x n matrix), and a scalar α exists such that αv is an eigenvector of a, then v must also be an eigenvector of a. However, this is not necessarily true.
Let's consider a counterexample to demonstrate this. Suppose we have the 2x2 identity matrix I:
I = [[1, 0],
[0, 1]]
In this case, any non-zero vector v will satisfy the condition αv = v for α = 1. However, not all non-zero vectors v are eigenvectors of I. In fact, the only eigenvectors of I are [1, 0] and [0, 1] with corresponding eigenvalues of 1.
Therefore, the statement is false. The existence of a scalar α such that αv is an eigenvector of a does not imply that v itself is an eigenvector of a.
Learn more about matrix on:
https://brainly.com/question/30715889
#SPJ4
You want to find the area of the front of a house whose shape is a triangle on top of a rectangle with a width of 11. The triangle's height is 13 and the rectangle's height is 7. What is the total area of the front of the house? Round to the nearest tenth. Do not include square units in your answer.
Answers
Answer: 148.5
Step-by-step explanation:
To find the area of this shape, comprised of a rectangle and a triangle, we can find the area of each shape and add them together.
The area of a triangle is 12⋅b⋅h. We are given the triangle's height, 13. The base of the triangle will be the same as the width of the rectangle, which we also know: 11. Now we can calculate the area of the triangle:
A = 1/2⋅b⋅h
A = 12⋅11⋅13
A = 71.5
Now we can find the area of the rectangle, which is l⋅w. The width of the rectangle is 11, which is the same as the base of the triangle; the length is 7:
A =l⋅w
A = 7⋅11
A = 77
Finally, we can add together the area of the triangle and the rectangle to find the total area:
A = 71.5 + 77 = 148.5
The total area of the front of a house will be 148.5.
What is mean by Rectangle?
A rectangle is a two dimension figure with 4 sides, 4 corners and 4 right angles. The opposite sides of the rectangle are equal and parallel to each other.
Given that;
A rectangle has a width = 11
The triangle's height = 13
The rectangle's height = 7
Now,
Since, The base of the triangle will be the same as the width of the rectangle.
Hence, The area of rectangle = 7 x 11
= 77
And, The area of triangle = 1/2 x 11 x 13
= 71.5
Thus, The total area of the front of a house = 77 + 71.5
= 148.5
Therefore, The total area of the front of a house will be 148.5.
Learn more about the rectangle visit:
https://brainly.com/question/398984
#SPJ2
A consumer watchdog organization estimates the mean weight of 1-ounce "Fun-Size"
candy bars to see if customers are getting full value for their money. A random sample
of 25 bars is selected and weighted, and the organization reports that a 95% confidence
interval for the true mean weight of the candy bars is 0.982 to 0.988 ounces.
a) What is the point estimate (=sample mean) from this sample?
b) What is the margin of error?
(Hint: find the distance between the sample mean and the upper limit).
c) Interpret the confidence level of 90% in the context of the problem?
Answers
Point estimate from the sample is 0.985, margin error is 0.003.
What is Confidence Interval?Confidence interval is defined as the interval which is the estimate for the parameter of the sample or population to be contained.
(a) To calculate point estimate or sample mean :
Point estimate is the mid point of the confidence interval.
Given that true mean weight of candy bars is 0.982 ounces to 0.988 ounces.
Point estimate = (0.982 + 0.988) / 2 = 1.97 / 2 = 0.985
(b) Margin error is the one half of the total width of the interval.
Margin error = (0.988 - 0.982) / 2 = 0.003
(c) The confidence level of 90% in this problem can be interpreted as , if we do the interval construction for many times, about 90% of the total constructed intervals has the true population mean of weight of fun size candy bars.
Hence the point estimate and margin error are 0.985 and 0.003 respectively.
Learn more about Confidence Interval here :
https://brainly.com/question/18914334
#SPJ1
(-4,-1), (5,3) find the midpoint of the two points
Answers
Answer: (0.5, 1)
Step-by-step explanation:
Hope this helped
Answer:
\( \huge{ \boxed{ \sf{ ( \: \frac{1}{2} \: , \: 1})}}\)
Step-by-step explanation:
\( \star { \sf{ \: Let \: the \: points \: be \: A \: and \: B}}\)
\( \star{ \sf{Let \: A \: (-4,-1) \: be \: (x1 \:, y1) \: and \: B \: ( \: 5 \:, 3 \: ) \: be \: (x2 \:, y2) }}\)
\( \boxed{ \underline{ \sf{ \: Midpoint = \: ( \: \frac{x1 + x2}{2} \:, \frac{y1 + y2}{2})} }}\)
\( \mapsto{ \sf{Midpoint = ( \frac{ - 4 + 5}{2}} \: ,\frac{ - 1 + 3}{2} }) \)
\( \underline{ \sf{Rmember}}\)!
The negative and positive integers are always subtracted but posses the sign of the bigger integer.The positive integers are always added and posses the positive ( + ) sign.The negative integers are always added but posses the negative ( - ) sign.\( \sf{Midpoint = ( \frac{ 1}{2} \:, \frac{2}{2}} )\)
\( \sf{Midpoint = ( \: \frac{1}{2 }, \: 1)}\)
Hope I helped!
Best regards! :D
~\( \sf{TheAnimeGirl}\)
Based on the percentage of total daily calories in the number of calories needed how many biscuits and packages of pemmican and packages of butter and cocoa just one person need each day
Answers
The problem asks for number of biscuits, packages of pemmican, and packages of butter and cocoa that a person needs each day, based on percentage of total daily calories. We need to calculate the quantities.
To determine the number of biscuits, packages of pemmican, and packages of butter and cocoa needed, we require additional information, such as the calorie content of each item and the total daily calorie requirement for an individual.Once we have the calorie content of each item and the total daily calorie requirement, we can calculate the percentage of calories provided by each item. From there, we can divide the total daily calorie requirement by the percentage of calories provided by each item to find the quantity needed.
Without the specific calorie content and total daily calorie requirement, it is not possible to provide a precise answer. It is important to know the specific values to accurately determine the quantities of biscuits, packages of pemmican, and packages of butter and cocoa needed for an individual's daily intake.
To learn more about total daily calories click here : brainly.com/question/30538642
#SPJ11
Find a function y=f(x) whose second derivative is y'=12x-2 at each point (x, y) on its graph and y= -x+5 is tangent to the graph at the point corrsponding to x=1
Please provide clear steps!
Answers
the function y = f(x) that satisfies the given conditions is y = 2x^3 - x^2 - 5x + C2, where C2 is a constant that can take any real value.
First, integrate y' with respect to x to find the first derivative y:
∫(y') dx = ∫(12x - 2) dx
y = 6x^2 - 2x + C1
Next, integrate y with respect to x to find the function f(x):
∫y dx = ∫(6x^2 - 2x + C1) dx
f(x) = 2x^3 - x^2 + C1x + C2
To determine the specific values of C1 and C2, we use the given condition that the line y = -x + 5 is tangent to the graph at x = 1.
Since the tangent line has the same slope as the function f(x) at x = 1, we can equate their derivatives:
f'(1) = -1
Taking the derivative of f(x), we have:
f'(x) = 6x^2 - 2x + C1
Substituting x = 1 and equating f'(1) to -1, we can solve for C1:
6(1)^2 - 2(1) + C1 = -1
6 - 2 + C1 = -1
C1 = -5
Now we have the values of C1 and C2. Plugging them back into the equation for f(x), we obtain the final function:
f(x) = 2x^3 - x^2 - 5x + C2
To learn more about tangent line : brainly.com/question/23416900
#SPJ11
You clean a community park for 6.5 hours. You earn $43.88. Find your hourly wage.
Answers
Step-by-step explanation:
you earned $43.88 for 6.5 hours of work.
an hourly rate means how much money you get for 1 hour of work.
to get that we need to divide now both by 6.5, as 6.5/6.5 = 1 hour.
and
43.88/6.5 = $6.750769231... per hour ≈ $6.75/ hour
79. Estimate the price (to the nearest dollar) of a table
in 1994 if the price of the table in 1973 was $500,
Note that the Consumer Price Index in 1973 was
44.4and in 1994 it was 148.2.
a. $1669
b. $505
c. $2100
d. $519
e. $1050
Answers
Answer:
a. $1669
Step-by-step explanation:
Price in 1994 = [ (CPI in 1994) / (CPI 1973) ] * (Price in 1973) =
[ 148.2 / 44.4 ] * 500 = 1668.91891892 = $1669 rounded to the nearest dollar.
the demand equation for video games is given by x = 960 − 30p where x is the number of video games and p is in dollars. find the value of p that maximizes the total revenue.
Answers
Value if p is $16 which maximizes the total revenue.
How to find the value of p that maximizes the total revenue?
We need to first find the total revenue equation and then maximize it. Here are the steps:
Step 1: Write the demand equation.
x = 960 - 30p
Step 2: Write the total revenue equation.
Total Revenue (R) = price (p) × quantity (x)
R = px
Step 3: Substitute the demand equation into the total revenue equation.
R = p(960 - 30p)
Step 4: Simplify the total revenue equation.
R = 960p - 30p²
Step 5: Differentiate the total revenue equation with respect to p.
dR/dp = 960 - 60p
Step 6: Set the derivative equal to zero to find the critical points.
0 = 960 - 60p
Step 7: Solve for p.
60p = 960
p = 960/60
p = 16
So, the value of p that maximizes the total revenue is $16.
Learn more about total revenue equation.
brainly.com/question/31008449
#SPJ11
The manager at Jessica's Furniture Store is trying to figure out how much to charge for a couch that just arrived. The couch was bought at a wholesale price of \$113.00$113.00dollar sign, 113, point, 00, and Jessica's Furniture Store marks up all furniture by 45%, percent.
Answers
Given the mark up of all furniture in the store, the price that the manager should charge for the couch that just arrived is $163.85.
How much should the manager charge for the couch that just arrived?Given that;
Purchase price = $113.00 marks up = 45%Selling price = ?First, we determine the mark price.
Since the Furniture Store marks up all furniture by 45%.
Mark up price = mark up × purchase price
Mark up price = 45% × $113.00
Mark up price = 0.45 × $113.00
Mark up price = $50.85
Now, the selling price will be;
Selling price = Purchase price + mark up price
Selling price = $113.00 + $50.85
Selling price = $163.85
Given the mark up of all furniture in the store, the price that the manager should charge for the couch that just arrived is $163.85.
Learn more about mark up prices here: https://brainly.com/question/2440726
#SPJ1