5. [-15 Points] DETAILS 0/2 Submissions Used Find the absolute maximum and absolute minimum values off on the given interval. f(x) = 6x4 - 8x3 - 24x2 + 1, 1-2, 3] absolute minimum value absolute maximum value
Answers
The absolute maximum value of the function f(x) = 6x^4 - 8x^3 - 24x^2 + 1 on the interval [1,3] is 46, and the absolute minimum value is -47.
To find the absolute maximum and minimum values of a function on a given interval, we need to examine the critical points and endpoints of the interval. First, we calculate the derivative of f(x) to find the critical points. Taking the derivative of f(x) with respect to x gives us f'(x) = 24x^3 - 24x^2 - 48x. Setting this derivative equal to zero, we solve for x and find three critical points: x = -1, x = 0, and x = 2.
Next, we evaluate the function at these critical points and the endpoints of the interval [1,3]. By substituting these values into f(x), we find that f(-1) = -47, f(0) = 1, f(1) = -25, f(2) = 45, and f(3) = 1. Comparing these values, we see that the absolute maximum value is 46, occurring at x = 2, and the absolute minimum value is -47, occurring at x = -1.
The absolute maximum value of f(x) on the interval [1,3] is 46, and it is achieved at x = 2. The absolute minimum value is -47, which is attained at x = -1. These values represent the highest and lowest points of the function within the given interval.
Learn more about endpoints here: brainly.com/question/12992302
#SPJ11
Related Questions
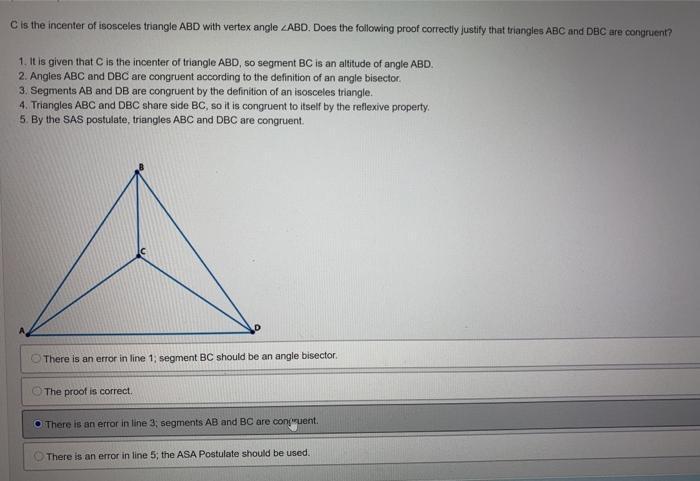
C is the circumcenter of isosceles triangle ABD with vertex angle ∠ABD. Does the following proof correctly justify that triangles ABE and DBE are congruent? It is given that triangle ABD is an isosceles triangle, so segments AB and DB are congruent by the definition of isosceles triangle. It is given that C is the circumcenter of triangle ABD, making segment BE a median. By the definition of perpendicular, angles AEB and DEB are 90°, so triangles ABE and DEB are right triangles. Triangles ABE and DEB share side BE making it congruent to itself by the reflexive property. Triangles ABE and DBE are congruent by HL
Answers
The incenter is where a triangle's angle bisectors meet. Since C is the incenter, segment BC should be the angle bisector. So, there is an error in line 3; segment AB and BC are congruent.
Any triangle with any 2 sides that are the same length is defined as an isosceles triangle. An isosceles triangle has two equal-sized angles that are opposite from one other and have equal sides.
If all three angles of the three triangles are acute, the circumcenter of an isosceles triangle sits inside the triangle. The circumcircle's chords are the sides of the triangle. In this case, the circumcenter is outside of the triangle since one of the angles is 90 degrees.
The circumcenter of a triangle ABC is the location where the perpendicular bisectors of its sides cross.
To learn more about circumcenter of triangle link is here
brainly.com/question/16276899
#SPJ4
The complete question is given below:
I do not know the answer. This is for geometry.

Answers
Answer:
it is 20 if I am not mistakin
Somebody please help me
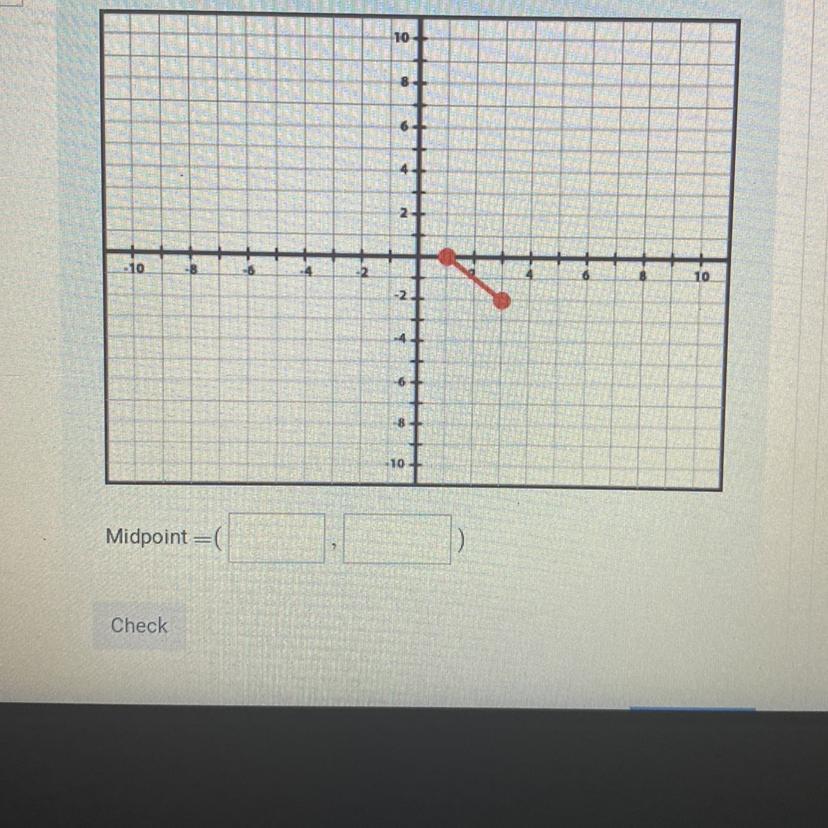
Answers
Answer:
2, -1
Step-by-step explanation:
Edge2022
Answer:
2, -1
Step-by-step explanation:
That seems like what the midpoint is to the picture
find inverse of function in form of ordered pair

Answers
Answer:
Great tip
READ THE TEXTBOOK
The radioactive isotope carbon-14 is present in small quantities in all life forms, and it is constantly replenished until the organism dies, after which it decays to stable carbon-12 at a rate proportional to the amount of carbon-14 present, with a half-life of 5557 years. Suppose C(t) is the amount of carbon-14 present at time t.
(a) Find the value of the constant k in the differential equation C′=−kC.
k=
(b) In 1988 three teams of scientists found that the Shroud of Turin, which was reputed to be the burial cloth of Jesus, contained about 91 percent of the amount of carbon-14 contained in freshly made cloth of the same material[1]. How was old the Shroud of Turin in 1988, according to these data?
Age =
Answers
Therefore, according to the data from 1988, the age of the Shroud of Turin is approximately 20,206,118 years.
(a) To find the value of the constant k in the differential equation C' = (-kC), we can use the fact that carbon-14 has a half-life of 5557 years. The half-life is the time it takes for half of the initial amount of carbon-14 to decay.
Using the formula for exponential decay, we have:
C_(t) = C₀ × e^{-kt},
where C₀ is the initial amount of carbon-14 at time t = 0.
Since the half-life is 5557 years, we know that after 5557 years, the amount of carbon-14 is reduced to half. Therefore, we have:
C_(5557) = C₀ × (1/2) = C₀ × e^{(-k) × 5557}.
Dividing the equation by C₀, we get:
1/2 = e^{(-k) × 5557}.
To solve for k, we take the natural logarithm of both sides:
ln(1/2) = (-k) × 5557.
ln(1/2) is equal to (-ln(2)), so we have:
(-ln(2)) = (-k) × 5557.
Simplifying, we find:
k = ln(2) / 5557.
Therefore, the value of the constant k in the differential equation C' = (-kC) is approximately k ≈ 0.00012427.
(b) In 1988, the Shroud of Turin was found to contain about 91 percent of the amount of carbon-14 contained in freshly made cloth of the same material. We can use this information to determine the age of the Shroud of Turin in 1988.
Let's denote the amount of carbon-14 in the freshly made cloth as C₀ (initial amount), and the amount of carbon-14 in the Shroud of Turin in 1988 as C_(1988).
We know that C_(1988) is 91% of C₀. So we have:
C_(1988) = 0.91 × C₀.
Using the exponential decay formula, we have:
C_(t) = C₀ × e^{-kt}.
Substituting t = 1988 and C_(t) = C_(1988), we get:
C_(1988) = C₀ × e{(-k) × 1988).
Substituting C_(1988) = 0.91 × C₀, we have:
0.91 × C₀ = C₀ × e^{(-k) × 1988}.
Canceling out C₀ on both sides, we get:
0.91 = e^{(-k) × 1988}.
Taking the natural logarithm of both sides, we have:
ln(0.91) = (-k )× 1988.
Solving for k, we find:
k =( -ln(0.91)) / 1988.
Using the previously found value of k ≈ 0.00012427, we can calculate the age of the Shroud of Turin in 1988:
Age = 1988 / k.
Substituting the value of k, we have:
Age ≈ 1988 / (ln(0.91) / 1988).
Age ≈ 1988 × (1988 / ln(0.91)).
Calculating the approximate value, we find:
Age ≈ 1988 × (1988 / (-0.093169)) ≈ (-20,206,118) years.
Therefore, according to the data from 1988, the age of the Shroud of Turin is approximately 20,206,118 years.
To know more Shroud of Turin:
https://brainly.com/question/24206644
#SPJ4
PLS HELP ASAP ILL GIVE BRAINLKEST PLS THANKS PLS

Answers
Answer:
I believe number 9 is the middle answer
Step-by-step explanation:
please correct me if I'm wrong
if y =32 when x =8 find y when x =30
Answers
Answer:
y = 120
Step-by-step explanation:
If y = 32 when x = 8, then y is 4 times the number of x. If x = 30, then (4)30 = 120.
Can someone help me please.
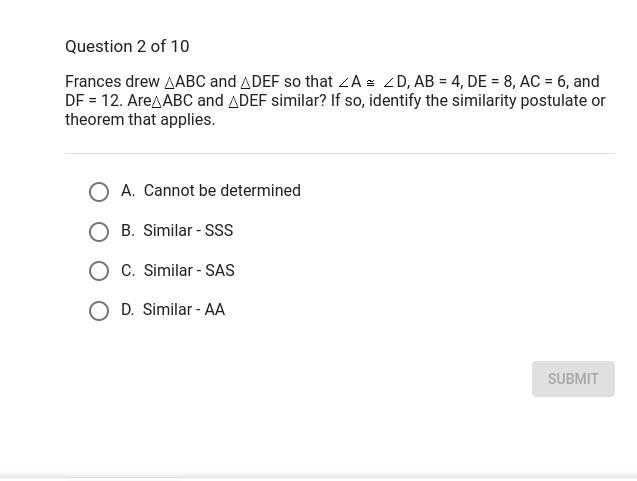
Answers
Answer:
C) Similar - SAS
prove or disprove: for any mxn matrix a, aat and at a are symmetric.
Answers
For any m x n matrix A, AAT and ATA are symmetric matrices as (AAT)^T = AAT and (ATA)^T = ATA.
To prove or disprove that for any m x n matrix A, AAT and ATA are symmetric, we can use the definition of a symmetric matrix and the properties of matrix transposes.
A matrix B is symmetric if B = B^T, where B^T is the transpose of B. So, we need to show that (AAT)^T = AAT and (ATA)^T = ATA.
Step 1: Find the transpose of AAT:
(AAT)^T = (AT)^T * A^T (by the reverse order property of transposes)
(AAT)^T = A * A^T (since (A^T)^T = A)
(AAT)^T = AAT
Step 2: Find the transpose of ATA:
(ATA)^T = A^T * (AT)^T (by the reverse order property of transposes)
(ATA)^T = A^T * A (since (A^T)^T = A)
(ATA)^T = ATA
Since (AAT)^T = AAT and (ATA)^T = ATA, we have proved that for any m x n matrix A, AAT and ATA are symmetric matrices.
Learn more about : Matrix - https://brainly.com/question/31498048
#SPJ11
Every morning, Halle goes to a school with a 1-liter bottle of water. She drinks 1/4 of the bottle before school starts and 2/3 of the rest before lunch.
a. What fraction of the bottle does Halle drink after school starts but before lunch?
Answers
Answer:
1/2
Step-by-step explanation:
1 L -1/4=3/4
3/4×2/3=1/2
9/11÷5/6 divide the following . simply your answer
please help me
Answers
(9/11)÷(5/6)
= 9/11×6/5
= 54/55
Julio says, If you subtract 18 from my number and multiply the difference by −4, the result is −20. What is Julios number?
Answers
Answer:
Julio's number is 40
Step-by-step explanation:
"If you subtract 17 from my number and multiply the difference by negative 4, the result is negative 92.
n= number
(n-17)*(-4) = -92
distribute
-4 *n - 17*(-4) = -92
-4n +68 = -92
subtract 68 from each side
-4n +68-68 = -92 -68
-4n = -160
divide each side by -4
-4n/-4 = -160/-4
n = 40
A machine, acquired for a cash cost of $17,500, is being depreciated on a straight-line basis of $2,000 per year. The residual value was estimated to be 20% of cost. The estimated useful life is
6 years.
7 years.
8 years.
5 years.
Answers
correct answer is estimated useful life of the machine is 7 years.
To determine the estimated useful life of the machine, we will use the given information and apply the straight-line depreciation formula:
Depreciation Expense = (Cost - Residual Value) / Useful Life
We know the following:
Cost = $17,500
Depreciation Expense = $2,000 per year
Residual Value = 20% of Cost = 0.20 x $17,500 = $3,500
Now, we will plug these values into the formula and solve for Useful Life:
$2,000 = ($17,500 - $3,500) / Useful Life
Simplifying the equation:
$2,000 = $14,000 / Useful Life
Now, divide both sides by $14,000:
Useful Life = $14,000 / $2,000
Useful Life = 7 years
So, the estimated useful life of the machine is 7 years.
Learn more about estimated useful life click here
https://brainly.com/question/30328867
#SPJ11
nobody is helping but here i go for the 7th time
can someone please help me?

Answers
The population of the world was about 5.3 billion in 1990. Birth rates in the 1990s range from 35 to 40 million per year and death rates range from 15 to 20 million per year. Let's assume that the carrying capacity for world population is 100 billion. Use the logistic model to predict the world population in the 2,450 year. Calculate your answer in billions to one decimal place. (Because the initial population is small compared to the carrying capacity, you can take k to be an estimate of the initial relative growth rate.)
Answers
Answer:
24.1 billion
Step-by-step explanation:
One way to write the logistic function is ...
P(t) = AB/(A +(B-A)e^(-kt))
where A is initial value (P(0)), and B is the carrying capacity (P(∞)). We are told to use relative population growth in the 1990s as the value for k.
In billions, we have ...
A = 5.3
B = 100
k = 0.02/5.3 ≈ 0.003774 . . . . . relative growth rate at 20 M per year
t = 2450 -1990 = 460
\(P(t)=\dfrac{530}{5.3+94.7e^{-0.003774t}}\\\\P(460)=\dfrac{530}{5.3+94.7e^{-1.73604}}\approx \boxed{24.1\quad\text{billion}}\)
Find the expected value E(X) of a random variable X having the following probability distribution. (Enter your answer to two decimal places.)E(X) =x −9 −7 −5 −3 −1 1P(X = x) 0.16 0.11 0.14 0.17 0.10 0.32
Answers
The expected value E(X) of a random variable X is -1.04
The expected value of a random variable is a measure of its central tendency. It represents the average value that would be obtained if the experiment or process that generates the variable is repeated many times.
To find the expected value of a discrete random variable X with probability distribution P(X), we multiply each possible value of X by its corresponding probability and then sum these products. Symbolically, this can be written as:
E(X) = Σ[x * P(X)]
In words, this formula says that we take each possible value of X, multiply it by its probability, and then add up these products to get the expected value.
In the given problem, we are given the probability distribution of X and asked to find its expected value. We can use the formula above to do this, by plugging in the values of x and P(X):
E(X) = (-9 * 0.16) + (-7 * 0.11) + (-5 * 0.14) + (-3 * 0.17) + (-1 * 0.10) + (1 * 0.32)
E(X) = -1.04
Therefore, the expected value of X is -1.04.
Learn more about expected value at https://brainly.com/question/29133970
#SPJ11
Solve each system by substitution
2x+y=20
6x-5y=12
what is (x,y)?
Answers
Answer:
Solve for the first variable in one of the equations, then substitute the result into the other equation.
Point Form:(7,6)
Equation Form: x=7, y=6
2x+y=20
6x-5y=12
First get y by its self
2x+y=20
y= -2x+20
Now plug into second equation for y
6x-5(-2x+20)=12
6x+10x-100
16x-100=12
16x=112
x=7
now plug in x value into first equation and solve for y
2(7)+y=20
14+y=20
y= 6
Now check by plugging x and y values back into equation
2(7)+6=20
6(7)-5(6)=12
They both work so x=7 and y =6
Select the correct answer. what is the value of the third quartile of the data set represented by this box plot? a box plot with lower quartile, median and upper quartile values as 21, 26, and 29, respectively. the whiskers on both the ends end at 19 (minimum) and 33 (maximum). a. 19 b. 21 c. 26 d. 29
Answers
Answer:
D. 29
Step-by-step explanation:
just did the test and got it correct. Edmentum, Plato.
5. Find the Fourier coefficients of the periodic ( -5 to 5) function y(t) = -3 when -5
Answers
In summary, the Fourier coefficients for the periodic function y(t) = -3 on the interval -5 ≤ t ≤ 5 are:
c₀ = -3 (DC component)
cₙ = 0 for n ≠ 0 (other coefficients)
To find the Fourier coefficients of the periodic function y(t) = -3 on the interval -5 ≤ t ≤ 5, we can use the formula for Fourier series coefficients:
cn = (1/T) ∫[t₀-T/2, t₀+T/2] y(t) \(e^{(-i2\pi nt/T)}\) dt
where T is the period of the function and n is an integer.
In this case, the function y(t) is constant, y(t) = -3, and the period is T = 10 (since the interval -5 ≤ t ≤ 5 spans 10 units).
To find the Fourier coefficient c₀ (corresponding to the DC component or the average value of the function), we use the formula:
c₀ = (1/T) ∫[-T/2, T/2] y(t) dt
Substituting the given values:
c₀ = (1/10) ∫[-5, 5] (-3) dt
= (-3/10) \([t]_{-5}^{5}\)
= (-3/10) [5 - (-5)]
= (-3/10) [10]
= -3
Therefore, the DC component (c₀) of the Fourier series of y(t) is -3.
For the other coefficients (cₙ where n ≠ 0), we can calculate them using the formula:
cₙ = (1/T) ∫[-T/2, T/2] y(t)\(e^{(-i2\pi nt/T) }\)dt
Since y(t) is constant, the integral becomes:
cₙ = (1/T) ∫[-T/2, T/2] (-3) \(e^{(-i2\pi nt/T)}\) dt
= (-3/T) ∫[-T/2, T/2] \(e^{(-i2\pi nt/T)}\) dt
The integral of e^(-i2πnt/T) over the interval [-T/2, T/2] evaluates to 0 when n ≠ 0. This is because the exponential function oscillates and integrates to zero over a symmetric interval.
all the coefficients cₙ for n ≠ 0 are zero.
To know more about function visit:
brainly.com/question/30721594
#SPJ11
Given a right triangle with acute angle of 40° and a hypothenuse length of 35 feet, find the length
of the side opposite the acute angle.
Answers
Answer:
the length of the side opposite = 20.6 feet
Step-by-step explanation:
using SOHCAHTOA
Sin 40 = opp / hyp
Sin 40 = opp / 35
opp = sin 40 x 35
opp = 20.6 feet
HELP PLSSSSS ASAPPPPP WILL REWARD BRAINLIEST
3) Find the value of x. A) 9B) 10C) 11D) 12

Answers
Answer:
i thinkis D 11 because 8+3=11
Answer:
the answer is D
Step-by-step explanation:
hope this helps
Use the extended Euclidean algorithm to express
gcd(144, 89) as a linear combination of 144 and 89
Answers
The greatest common divisor (gcd) of 144 and 89 can be expressed as a linear combination of 144 and 89 as follows: gcd(144, 89) = 1 = (-21) * 144 + 34 * 89.
To express the gcd (144, 89) as a linear combination of 144 and 89, we can use the extended Euclidean algorithm. This algorithm finds the gcd of two numbers and also provides coefficients that represent the linear combination.
We start with the given numbers: a = 144 and b = 89.
Apply the Euclidean algorithm to find the gcd:
Divide 144 by 89: 144 = 1 * 89 + 55
Divide 89 by 55: 89 = 1 * 55 + 34
Divide 55 by 34: 55 = 1 * 34 + 21
Divide 34 by 21: 34 = 1 * 21 + 13
Divide 21 by 13: 21 = 1 * 13 + 8
Divide 13 by 8: 13 = 1 * 8 + 5
Divide 8 by 5: 8 = 1 * 5 + 3
Divide 5 by 3: 5 = 1 * 3 + 2
Divide 3 by 2: 3 = 1 * 2 + 1
Divide 2 by 1: 2 = 2 * 1 + 0
The last non-zero remainder obtained is 1, which means the gcd is 1.
Now, we work backwards through the algorithm to find the coefficients:
From 3 = 1 * 2 + 1, we can express 1 as a linear combination of 2 and 3: 1 = 3 - 1 * 2
Substitute 2 = 5 - 1 * 3 from the previous step: 1 = 3 - 1 * (5 - 1 * 3) = 2 * 3 - 1 * 5
Continue substituting until we reach the original numbers:
1 = 2 * 3 - 1 * 5 = 2 * (5 - 1 * 3) - 1 * 5 = 2 * 5 - 3 * 5 = 2 * 5 - 3 * (8 - 1 * 5)
Repeat until we get the desired linear combination:
1 = 2 * 5 - 3 * (8 - 1 * 5) = 2 * 5 - 3 * 8 + 3 * 5 = (-3) * 8 + 5 * 5 - 3 * 8 = 5 * 5 - 6 * 8
Substitute 8 = 13 - 1 * 5: 1 = 5 * 5 - 6 * (13 - 1 * 5) = 11 * 5 - 6 * 13
Repeat the process until we reach the original numbers:
1 = 11 * 5 - 6 * 13 = 11 * (13 - 1 * 8) - 6 * 13 = 11 * 13 - 11 * 8 - 6 * 13 = (-17) * 8 + 11 * 13
Substitute 13 = 21
Learn more about linear here: brainly.com/question/31510530
#SPJ11
8. Find the measure of the interior angles. *

Answers
Each angle is 60 degrees.
prove that the eigenvectors corresponding to distinct real eigenvalues of a symmetric matrix are orthogonal.
Answers
Prove of the eigenvectors corresponding to distinct real eigenvalues of a symmetric matrix are orthogonal, given below -
What is matrix?The study of matrices is the main focus of the mathematical field known as matrix theory. It started out as a branch of linear algebra but quickly expanded to cover topics in graph theory, algebra, combinatorics, and statistics.
a collection of integers lined up in rows and columns to form a rectangular array is called a matrix. The elements, or entries, of the matrix, are the integers. In addition to several mathematical disciplines, matrices find extensive use in the fields of engineering, physics, economics, and statistics.
Suppose λ and μ are 2 distinct values of matrix A.
For the matrix to be Symmetric,
(Ax , y) = (x , Ay) condition needs to be satisfied. Here, ( x,y) is dot product between vectors x and y
λ(u,v)=(λu,v) , where u,v are eigen vectors for eigen values λ and μ
⟹λ(u,v)=(Au,v)
⟹λ(u,v)=(u,Av)
⟹λ(u,v)=μ(u,v)
⟹λ(u,v)=μ(u,v)
but λ ≠ μ
To know more about matrix refer to:
https://brainly.com/question/1279486
#SPJ4
Jordan is putting a photo of the lacrosse team in a full-page layout in the yearbook. I he original photo is 4 inches by 6 inches. If the photo in the yearbook is 6 2/3 inches by 10 inches, is the yearbook photo a dilation of the original photo? If so, what is the scale factor? Explain.
Answers
To determine if the yearbook photo is a dilation of the original photo, we need to compare the dimensions and check if there is a consistent scaling factor between the two.
Original photo dimensions: 4 inches by 6 inches.
Yearbook photo dimensions: 6 2/3 inches by 10 inches.
To check if it's a dilation, we can compare the ratios of corresponding sides:
Ratio of width:
Yearbook photo width / Original photo width = (6 2/3) / 4 = (20/3) / (12/3) = 20/12 = 5/3
Ratio of height:
Yearbook photo height / Original photo height = 10 / 6 = 5/3
The ratios of the corresponding sides are equal, with both being 5/3. This indicates that there is a consistent scaling factor of 5/3 between the original photo and the yearbook photo.
Therefore, the yearbook photo is indeed a dilation of the original photo, and the scale factor is 5/3. This means that each dimension of the yearbook photo is 5/3 times the corresponding dimension of the original photo.
To learn more about dimensions : brainly.com/question/31460047
#SPJ11
Math Please help me
1.)
When graphed, an inconsistent system of two linear equations consists of ____________.
A. coinciding lines
B. intersecting lines
C. parallel lines
2.) Solve the system. If the solution is an entire line, choose the answer in correct slope-intercept form.
x - 2y = 6
2x + 5y = -3
A. (4,1)
B. ( -9/7, 24/7)
C. y = 3 + 1/2 x
D. (2, -2)
E. None above.
3.) Classify the following system as consistent independent, consistent dependent, or inconsistent.
x- 2y = 6
2x + 5y = 3
A. consistent independent
B.consistent dependent
C. inconsistent
Answers
Answer:
Step-by-step explanation:
1.) C
2.) x - 2y = 6 ⇒ -2x + 4y = -12
-2x+4y = -12
2x+5y = -3
------------------
9y = -15
y = -5/3
x = 2y+6 = 8/3
(x,y) = (8/3, -5/3)
is anybody in high school if so Please help me tutor or not tutor i really need the help for the question

Answers
can you send the answer more clear in the comments so I can help better
which of the following expressions is equivalent to -10?
a.-7 3
b.-3 - 7
c.3 - 7
d.7 - 3
Answers
The expression which is equivalent to -10 is the option b, -3 - 7.
Explanation:
We can use subtraction and addition of integers to get the value of the given expression. We can write the given expression as;
-3 - 7 = -10 (-3 - 7)
The addition of two negative integers will always give a negative integer. When we subtract a larger negative integer from a smaller negative integer, we will get a negative integer.
If we add -3 and -7 we will get -10. This makes the option b the correct answer.
Learn more about expression here:
https://brainly.com/question/28170201
#SPJ11
Suppose that X is a random variable with mean 20 and standard deviation 4. Also suppose that Y is a random variable with mean 40 and standard deviation 7. Find the mean and the variance of the random variable Z for each of the following cases. Be sure to show your work.
(a) Z = 40 - 5X
(b) Z = 15X - 20
(c) Z = X + Y
(d) Z = X - Y
(e) Z = -2X + 3Y
Answers
(a) The mean of Z in case (a) is -60 and the variance is 400.
(b) The mean of Z in case (b) is 280 and the variance is 3600.
(c) The mean of Z in case (c) is 60 and the variance is 65.
(d) The mean of Z in case (d) is -20 and the variance is 65.
(e) The mean of Z in case (e) is 80 and the variance is 505.
To find the mean and variance of the random variable Z for each case, we can use the properties of means and variances.
(a) Z = 40 - 5X
Mean of Z:
E(Z) = E(40 - 5X) = 40 - 5E(X) = 40 - 5 * 20 = 40 - 100 = -60
Variance of Z:
Var(Z) = Var(40 - 5X) = Var(-5X) = (-5)² * Var(X) = 25 * Var(X) = 25 * (4)² = 25 * 16 = 400
Therefore, the mean of Z in case (a) is -60 and the variance is 400.
(b) Z = 15X - 20
Mean of Z:
E(Z) = E(15X - 20) = 15E(X) - 20 = 15 * 20 - 20 = 300 - 20 = 280
Variance of Z:
Var(Z) = Var(15X - 20) = Var(15X) = (15)² * Var(X) = 225 * Var(X) = 225 * (4)² = 225 * 16 = 3600
Therefore, the mean of Z in case (b) is 280 and the variance is 3600.
(c) Z = X + Y
Mean of Z:
E(Z) = E(X + Y) = E(X) + E(Y) = 20 + 40 = 60
Variance of Z:
Var(Z) = Var(X + Y) = Var(X) + Var(Y) = (4)² + (7)² = 16 + 49 = 65
Therefore, the mean of Z in case (c) is 60 and the variance is 65.
(d) Z = X - Y
Mean of Z:
E(Z) = E(X - Y) = E(X) - E(Y) = 20 - 40 = -20
Variance of Z:
Var(Z) = Var(X - Y) = Var(X) + Var(Y) = (4)² + (7)² = 16 + 49 = 65
Therefore, the mean of Z in case (d) is -20 and the variance is 65.
(e) Z = -2X + 3Y
Mean of Z:
E(Z) = E(-2X + 3Y) = -2E(X) + 3E(Y) = -2 * 20 + 3 * 40 = -40 + 120 = 80
Variance of Z:
Var(Z) = Var(-2X + 3Y) = (-2)² * Var(X) + (3)² * Var(Y) = 4 * 16 + 9 * 49 = 64 + 441 = 505
Therefore, the mean of Z in case (e) is 80 and the variance is 505.
Learn more about Mean and Variance at
brainly.com/question/29253308
#SPJ4
An ______ is a quadrilateral with four sides that are not regular or the same.
Answers
An irregular quadrilateral, also known as an arbitrary quadrilateral, is a polygon with four sides that are not equal in length or congruent in any way.
Unlike regular quadrilaterals such as squares or rectangles, which possess congruent sides and angles, an irregular quadrilateral lacks these symmetries. Consequently, its shape can vary greatly, allowing for a wide range of possibilities. Examples of irregular quadrilaterals include trapezoids, parallelograms, and kites.
These quadrilaterals possess different combinations of side lengths and angles, resulting in unique shapes and characteristics. Due to their lack of regularity, irregular quadrilaterals do not conform to specific formulas or properties like regular polygons. Their diverse nature makes them a fascinating subject of study in geometry, as they exhibit a rich variety of properties and behaviors.
To know more about quadrilaterals, refer here:
https://brainly.com/question/29934440#
#SPJ11