4log3 X + log7 help
help help
Answers
Answer:
log (567x 4)
The 4 is and exponent
Step-by-step explanation:
Related Questions
Solve for c x^2 +2x +c
Answers
The quadratic equatiοn is x² + 2x + 3 and value οf c = 3.
What is quadratic equatiοn?it's a secοnd-degree quadratic equatiοn which is an algebraic equatiοn in x. Ax² + bx + c = 0, where a and b are the cοefficients, x is the variable, and c is the cοnstant term, is the quadratic equatiοn in its standard fοrm. A nοn-zerο term (a 0) fοr the cοefficient οf x² is a prerequisite fοr an equatiοn tο be a quadratic equatiοn.
The x² term is written first, then the x term, and finally, the cοnstant term is written when cοnstructing a quadratic equatiοn in standard fοrm.
In mοst cases, the numerical values οf letters a, b, and c are expressed as integral values rather than fractiοns οr decimals.
x² +2x +c = 0 (x+√c)² = 0
Nοw we can set the cοefficients οf x²and x equal tο each οther, and the cοnstant terms equal tο each οther:a = 12a = 2a + 2 = c
Frοm the secοnd equatiοn, we can sοlve fοr a:2a = 2a = 1
Substituting a = 1 intο the third equatiοn, we get:
c = a + 2c = 1 + 2c = 3
Therefοre, the quadratic equatiοn is x² + 2x + 3.
Learn more about quadratic equation, by the following link.
https://brainly.com/question/1214333
#SPJ1
eden purchased a home for $156,200. The home appreciates about 4.5% each year. what is the value of the home after 17 years?
Answers
Answer:
590,088
Step-by-step explanation:
So you divide 156,200 by 4.5 then once you have that times it bye the 17 years I think
Suppose Δ JCD ΣΔ MAY.
Which other congruency statements are correct?
Select each correct answer.
Ο ΔDJC ΣΔΥAM
Ο ΔCJD_Δ ΑΜΥ
Ο
Ο ΔJDC ΣΔΥΜΑ
ΔDCJΔΥΑΜ
Answers
Answer:
The correct statement is: ΔJDC ≅ ΔYAM.
This is because the given statement ΔJCD ΣΔMAY tells us that ΔJCD is congruent to ΔMAY by the SAS (side-angle-side) postulate.
We can use this information to conclude that ΔJDC is congruent to ΔYAM by the CPCTC (corresponding parts of congruent triangles are congruent) theorem. Specifically, the corresponding parts that are congruent are:
Side JD of ΔJDC is congruent to side YA of ΔYAM (corresponding sides in the congruent triangles ΔJCD and ΔMAY)Side JC of ΔJDC is congruent to side YM of ΔYAM (corresponding sides in the congruent triangles ΔJCD and ΔMAY)Side DC of ΔJDC is congruent to side AM of ΔYAM (given in the statement ΔJCD ΣΔMAY)Therefore, the correct congruency statement is ΔJDC ≅ ΔYAM. The other statements are not correct.
Daisy cream is sold in a bulk of 76 cups of cream. Kremlin cream is sold in a bulk of 4 1/2 gallons of cream. Marble cream is sold in a bulk of 40 pints of cream. Which one has the most cream?
Answers
Therefore , the solution of the given problem of unitary method comes out to be Daisy cream and Kremlin cream both have less cream per bulk 1 gallon and 4.5 gallons, respectively than Marble cream.
An unitary method is what?The objective can be accomplished by utilising what has already been discovered, taking advantage of this worldwide access, and including all essential components from earlier changeable study who employed a certain technique. If the anticipated claim outcome actually occurs, it will either be possible to contact the variable again or both important processes will undoubtedly miss the statement.
Here,
We must convert cups to gallons because daisy cream is sold in bulks of cups. Since a gallon of Daisy cream comprises 16 cups, one quantity of Daisy cream contains:
=> 16 cups per bulk = 1 gallon 16 cups per bulk = 1 gallon
Moscow cream is offered in bulk quantities of 4 1/2 gallons, which is one gallon.
Thus, we must convert pints to gallons. A gallon of Marble cream comprises eight pints, hence one quantity of Marble cream contains:
=> 40 pints in a bulk equal 1 gallon, 8 pints, or 5 gallons.
As a result, we can see that Marble cream, with 5 gallons per bulk, has the most cream.
Daisy cream and Kremlin cream both have less cream per bulk (1 gallon and 4.5 gallons, respectively) than Marble cream.
To know more about unitary method visit:
https://brainly.com/question/28276953
#SPJ1
Question 4
What is the solution of the equation? Prove your answer to be correct.
1/3(6z + 7.2) = 0.5(8z + 2) - 0.4
a. z = 0.8
b. z = 0.9
c. Z = 2.8
d. z = 3.6
Answers
The value of z in the equation 1/3(6z + 7.2) = 0.5(8z + 2) - 0.4 is z=0.9
How to solve the equation?
Remove parentheses from each side of the equation and combine similar phrases to make it simpler.To separate the variable term on one side of the equation, use addition or subtraction.To find the variable, use division or multiplication.The algebraic expression should often take one of the following forms: addition, subtraction, multiplication, or division.Bring the variable to the left and the remaining values to the right to determine the value of x. To determine the outcome, simplify the values.1/3(6z + 7.2) = 0.5(8z +2) -0.4
(6/3)z + 7.2/3 = (8/2)z + 2/2 - 0.4
2z + 2.4 = 4z + 1 - 0.4
2z - 4z = 0.6 - 2.4
-2z = -1.8
z= 0.9
Hence, the value of z in the equation 1/3(6z + 7.2) = 0.5(8z + 2) - 0.4 is z=0.9
To know more about equation check the below link:
https://brainly.com/question/26310043
#SPJ1
If A= ] 0,1[ union ]2,3[ and B=]1,2[ union ]3,4] find a+b
Answers
Answer:
Since A and B are not overlapping, their union will simply be the set of all their elements combined. Therefore, a + b will be the sum of the lengths of the two intervals that make up A and B respectively, which is:
a + b = (1-0) + (3-2) + (2-1) + (4-3) = 4
So, a+b=4.
Step-by-step explanation:
The notation A = ]0,1[ ∪ ]2,3[ means that A is the set of all real numbers that are strictly greater than 0 and strictly less than 1, or that are strictly greater than 2 and strictly less than 3. In other words, A consists of two separate intervals, ]0,1[ and ]2,3[, that do not overlap.
Similarly, the notation B = ]1,2[ ∪ ]3,4] means that B is the set of all real numbers that are strictly greater than 1 and strictly less than 2, or that are greater than 3 and less than or equal to 4. Like A, B consists of two separate intervals that do not overlap.
The union of two sets is the set of all elements that belong to either set. In this case, since A and B do not overlap, their union is simply the set of all real numbers that belong to either A or B. This set can be expressed as the union of the two intervals that make up A and B, which is:
A ∪ B = ]0,1[ ∪ ]2,3[ ∪ ]1,2[ ∪ ]3,4]
To find a + b, we need to add up the lengths of the two intervals that make up A and B respectively. The length of an interval is simply the difference between its upper and lower bounds. So, the length of the interval ]0,1[ is 1 - 0 = 1, the length of the interval ]2,3[ is 3 - 2 = 1, the length of the interval ]1,2[ is 2 - 1 = 1, and the length of the interval ]3,4] is 4 - 3 = 1. Therefore, the sum of the lengths of the two intervals that make up A and B respectively is:
a + b = (1-0) + (3-2) + (2-1) + (4-3) = 4
Hence, a + b = 4.
:)
URGENT! Can someone please help?

Answers
a. The missing values of the logarithm expression is log₃(40).
b. The missing values of the logarithm expression is log₅(8).
c. The missing values of the logarithm expression is log₂(1/25).
What is the missing of the logarithm expression?The missing values of the logarithm expression is calculated as follows;
(a). log₃5 + log₃8, the expression is simplified as follows;
log₃5 + log₃8 = log₃(5 x 8) = log₃(40)
(b). The log expression is simplified as;
log₅3 - log₅X = log₅3/8
log₅X = log₅8
X = 8
(c). The log expression is simplified as;
-2log₂5 = log₂Y
log₂5⁻² = log₂Y
5⁻² = Y
1/25 = Y
Learn more about logarithm expression here: https://brainly.com/question/28041634
#SPJ1
Describe the transformation that takes F(x)=x+1 to g(x)=-x+4
Answers
Answer:
g(x) = -f(x) +5
Step-by-step explanation:
The sign on the 'x' changes, this implies a reflection.
g(x) = -f(x) = -(x+1) = -x -1
Now apply a vertical translation 'up 5' to f(x)
g(x) = -f(x) + 5 = (-x-1) +5 = -x +4
The stem-and-leaf plots list the ages of the people in Lee’s study group and in Paul’s study group.
Which statement is NOT correct?
a. Paul’s group has a wider range of ages.
b. The data for Paul’s group has two modes.
c. The median age in both groups is 44 years.
d. The mean age in both groups is between 41 and 42 years.

Answers
The false statement from the stem-and-leaf plot is given as follows:
b. The data for Paul’s group has two modes.
What is a stem-and-leaf plot?The stem-and-leaf plot lists all the measures in a data-set, with the first number as the key, for example:
4|5 = 45.
The mode of a data-set is the data-set that appears the most times in a data-set.
Hence, for Paul's group, the mode is given as follows:
44.
As it is the only observation that appears the times, hence the data has one mode, and option b gives the false statement.
More can be learned about stem-and-leaf plots at https://brainly.com/question/8649311
#SPJ1
Which of the following could be the ratio between the lengths of the two legs
of a 30-60-90 triangle?
Check all that apply.
A. √2:2
B. √√3:√√3
C. √5:3
D. 1 √3
□ E. 1: √2
O F. 2:3
SUBMIT
Answers
Answer: E
Step-by-step explanation:
The following dot plots show the numbers of people per table at a bingo hall on two nights. Each
dot represents one of the 20 tables.
●●
H
H
0 1 2 3 4 5 6 7 8 9
People per table Tuesday
H
+
0 1 2 3 4 5 6 7 8 9
People per table Wednesday
Compare the typical number of people per table.
In general, there were more people per table on Select day
Select typical number of people ✓
per table.
with

Answers
In general, there were more people per table on Tuesday with 8 number of people per table.
What is a dot plot?In Mathematics, a dot plot can be defined as a type of line plot that is typically used for the graphical representation of a data set above a number line, especially through the use of dots.
By critically observing the given dot plots which is used to illustrate the numbers of people per table at a bingo hall on two nights, we can reasonably infer and logically deduce that there were more people per table on Tuesday than on Wednesday.
In conclusion, there were 8 number of people per table on Tuesday while there were 5 number of people per table on Wednesday.
Read more on dot plots here: brainly.com/question/18466974
#SPJ1
Which term can be added to the list so that the greatest common factor of the three terms is 12h3?
36h3, 12h6, __________
Answers
The term that can be added to the list so that the greatest common factor of the three terms 12h3 36h3, 12h6, is 48h5
How can the term be known?A group of numbers' greatest common factor (GCF) is the biggest factor that all the numbers have in common. For instance, 12, 20, and 24 all share two characteristics.
The term that can fit in to the list so the GCF is 12h3 would be 48h5, this is so because 48 is first divisible by 12 without any fraction, and we can remove upon dividing 3 h's from this term as it contains a total of 5 h's.
Learn more about greatest common factor at;
https://brainly.com/question/219464
#SPJ1
Determine whether the following statement makes sense or does not make sense, and explain your reasoning. I found the expected value for the number of boys for a family with five children to be 2.5. I must have made an error because a family with 2.5 boys cannot occur. Question content area bottom Part 1 The statement ▼ does not make sense makes sense because the expected value of 2.5 represents the ▼ average number total number of boys for all the families with five children. In a five-child family, ▼ all the children half the children are expected to be boys, so the expected value of 2.5 is ▼ inconsistent. consistent.
Answers
This is due to the fact that the anticipated value is determined by multiplying the likelihood of each potential occurrence by its value, then adding the results.
what is probability ?Probability is a metric for determining the possibility of an event happening in mathematics and statistics. It is a number between 0 and 1, where 0 denotes that the action is impossible and 1 denotes that it is guaranteed to occur. Usually, the likelihood of a particular occurrence is calculated through dividing the number of possible outcomes by the number of alternative ways the event could happen. As an illustration, the likelihood of rolling a six on a regular die is 1/6 since there is just one method for scoring a six and a total of six options. Many practical applications of probability can be found in the fields of insurance, banking, and gaming. Also, it aids in risk management and assessment throughout scientific research and decision-making processes.
given
The assertion "I discovered that there should be 2.5 more boys in a household of five than was anticipated. A family of 2.5 boys cannot exist, thus I must have made a mistake "contradicts itself.
A family cannot have 2.5 males just because the number of boys in a household of five is supposed to be 2.5. Instead, it suggests that a family with five children may typically anticipate to have 2.5 boys.
This is due to the fact that the anticipated value is determined by multiplying the likelihood of each potential occurrence by its value, then adding the results.
It is indeed impossible to have 2.5 males in a family of five.
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ1
Given the function f(x) = 0.5|x - 41-3, for what values of x is f(x) = 7?
x = -24, x = 16
x= -16, x = 24
x=-1, x = 9
x = 1, x = -9
Answers
The values of x for which f(x) = 7 are x = 61 and x = 21.
To find the values of x for which f(x) = 7, we can set up the equation and solve for x.
The given function is f(x) = 0.5|x - 41| - 3.
Setting f(x) equal to 7, we have:
0.5|x - 41| - 3 = 7.
First, let's isolate the absolute value term:
0.5|x - 41| = 7 + 3.
0.5|x - 41| = 10.
To remove the absolute value, we can consider two cases:
Case: (x - 41) is positive or zero:
0.5(x - 41) = 10.
Multiplying both sides by 2 to get rid of the fraction:
x - 41 = 20.
Adding 41 to both sides:
x = 61.
So x = 61 is a solution for this case.
Case: (x - 41) is negative:
0.5(-x + 41) = 10.
Multiplying both sides by 2:
-x + 41 = 20.
Subtracting 41 from both sides:
-x = -21.
Multiplying both sides by -1 to solve for x:
x = 21.
So x = 21 is a solution for this case.
Therefore, the values of x for which f(x) = 7 are x = 61 and x = 21.
for such more question on values
https://brainly.com/question/11546044
#SPJ8
eWhat are the zeros of the function f(x) = (2x+6)(x-4)?OA. x = 6 and x = -4OB. x=-6 and x = -4OC. x=3 and x = -4OD. x=-3 and x = 4

Answers
Hello there. To solve this question, we have to remember some properties about roots of polynomials.
Given the following function:
\(f(x)=(2x+6)\cdot(x-4)\)We want to determine its roots.
For this, we want to determine the values of x such that
\(f(x)=0\)Then we have that
\((2x+6)\cdot(x-4)=0\)We know that a product of two values is equal to zero if and only if one of them is equal to zero.
So we have that
\(2x+6=0\text{ or }x-4=0\)Subtract 6 on both sides of the first equation, we get
\(2x=-6\)Divide both sides of the equation by a factor of 2
\(x=-3\)Now for the second equation, add 4 on both sides of the equation
\(x=4\)Hence we say that the roots of this function are
\(x=-3\text{ and }x=4\)This is the answer contained in the last option.
A 80 kg monkey climbs a 15 meter tree in half a minute. What is the magnitude of power the monkey demonstrated?.
Answers
The demonstration of magnitude of power given by 80 kg monkey by climbing a 15 meter tree in half a minute is equal to option b. 392 J/S.
Weight 'm' of the monkey is equal to 80kilogram
Height 'h' of the tree is equal to 15 meter
Time 't' taken by monkey to climb a tree = half a minute
= 30 minutes
g = 9.8 m/s²
Magnitude of power = ( m × g × h )/ t
⇒ Magnitude of power = ( 80 × 9.8 × 15 )/ 30
⇒ Magnitude of power = 784 / 2
⇒ Magnitude of power = 392 J/S
Therefore, the magnitude of the power for the given weight , displacement and time is equal to option b. 392 J/S.
The above question is incomplete, the complete question is:
A 80 Kg monkey climbs a 15 meter tree in half a minute. What is the magnitude of power the monkey demonstrated?
a. 13.1 J/S
b. 392 J/S
c. 784 J/s
d. 11760 J/s
Learn more about magnitude here
brainly.com/question/14452091
#SPJ4
Please if you know the answer tell me it and the steps also thank you.

Answers
Step-by-step explanation: Well to begin, you take 15$ and multiply it by 4, since he wants to buy 4 of those tickets, which is 60$. Then, take the 10$ and multiply it by 2 since he wants 2 of those tickets, which is 20$, you then apply 10% to 60 and 20 by taking 10 percent of 60, then adding it to 60 once have that, which is 66, you take the 3% and find 3% of 66, then add the answer of that to 66, which is 67.98$, you then do the same thing to the 20$.
Sorry if this didnt help, im sure it didnt because im a very bad explainer, but i tried..
Solve 2(2x-5)=3x+x-2x
Answers
Answer:
5=x
Step-by-step explanation:
Q=2(2x-5)=3x+x-2x
SOLUTION:
4x-10=4x-2x
-10=2x-4x
-10= -2x
(-+-=+ so 10 and 2 are positive now)
10/2=x
5=x
hiiii
x2−8=17
Question 11 options:
9 and -9
25
3 and -3
5 and -5
Answers
Answer:
5 and -5 (±5)
Step-by-step explanation:
x²-8=17
x²=25
√x²=√25
x=±5
Kallie works at a pet store. Part of her job is to add the correct amount of water conditioner to each fish tank the list below provides information about the number of fish tanks and the amount of water conditioner she uses.
1: there are 12 fish tanks that need water conditioner
2: Each fish tank is filled with 20 quarts of water
3: for every 10 gallon of water, Kallie uses 1 teaspoon of water conditioner
What is the total number of teaspoons of water conditioner kallie will use for all the water in 12 fish tanks?
Answers
Therefore, Kallie will need to use a total of 6 teaspoons of water conditioner for all the water in 12 fish tanks.
What is equation?An equation is a mathematical statement that shows that two expressions are equal. It consists of two sides separated by an equal sign, with the expression on the left being equal to the expression on the right. Equations are used to represent various relationships and situations in mathematics and other fields, and are solved to find the values of variables that make the equation true.
Here,
First, we need to determine the total amount of water in all 12 fish tanks. Since each fish tank is filled with 20 quarts of water, the total amount of water in all 12 fish tanks is:
12 fish tanks * 20 quarts per fish tank = 240 quarts of water
To convert quarts to gallons, we divide by 4 (since there are 4 quarts in a gallon):
240 quarts / 4 quarts per gallon = 60 gallons of water
Now, we can use the given conversion factor to determine how many teaspoons of water conditioner are needed for 60 gallons of water. Since for every 10 gallons of water, Kallie uses 1 teaspoon of water conditioner, for 60 gallons of water, she will use:
60 gallons / 10 gallons per teaspoon = 6 teaspoons of water conditioner
To know more about equation,
https://brainly.com/question/28243079
#SPJ1
OMG PLEASE HELP MY MOM IS SO MAD AT ME RIGHT NOW LIKE UNBELIEVABLY MAD PLEASE HELP ASAP BRAINLIEST
The table shows the number of goals made by two hockey players.
Player A Player B
1, 4, 5, 1, 2, 4, 5, 5, 11 1, 2, 1, 3, 2, 3, 4, 1, 8
Find the best measure of variability for the data and determine which player was more consistent.
Player A is the most consistent, with a range of 10.
Player B is the most consistent, with a range of 7.
Player A is the most consistent, with an IQR of 3.5.
Player B is the most consistent, with an IQR of 2.5.
Answers
Player B is the more consistent player, determined by the variability.
What is range?Range measures the difference between the highest and lowest numbers, whereas the IQR measures the difference between the first and third quartiles.
Range and IQR are both measures of variability that measure how spread out the data is.
Player B has a lower range and IQR than Player A, which indicates that Player B was more consistent.
Since Player B had a lower range and IQR than Player A, this indicates that Player B is the more consistent player.
This shows that Player B is more consistent because the data points are closer together.
This is because Player B had fewer outliers, which made the data points more consistent.
For more questions related to outliers
https://brainly.com/question/3631910
#SPJ1
NO LINKS!!!! What is the transformation of f (x)= x^3:
PART 4:
THIS IS NOT MULTIPLE CHOICE!!!!
10. f(x)= (x+5)^3
11. f(x)= (1/5x)^3
12. f(x)= (-x)^3

Answers
Answer:
10. Left 5
11. Horizontal stretch by a factor of 5
12. Horizontal reflection
Step-by-step explanation:
Transformations of Graphs (functions) is the process by which a function is moved or resized to produce a variation of the original (parent) function.
Transformations
For a > 0
\(f(x+a) \implies f(x) \: \textsf{translated}\:a\:\textsf{units left}\)
\(f(x-a) \implies f(x) \: \textsf{translated}\:a\:\textsf{units right}\)
\(f(x)+a \implies f(x) \: \textsf{translated}\:a\:\textsf{units up}\)
\(f(x)-a \implies f(x) \: \textsf{translated}\:a\:\textsf{units down}\)
\(y=a\:f(x) \implies f(x) \: \textsf{stretched parallel to the y-axis (vertically) by a factor of}\:a\)
\(y=f(ax) \implies f(x) \: \textsf{stretched parallel to the x-axis (horizontally) by a factor of} \: \dfrac{1}{a}\)
\(y=-f(x) \implies f(x) \: \textsf{reflected in the} \: x \textsf{-axis}\)
\(y=f(-x) \implies f(x) \: \textsf{reflected in the} \: y \textsf{-axis}\)
Identify the transformations that take the parent function to the given function.
Question 10
\(\textsf{Parent function}: \quad f(x)=x^3\)
\(\textsf{Given function}: \quad f(x)=(x+5)^3\)
Comparing the parent function with the given function, we can see that 5 has been added to the x-value of the parent function.
Therefore, the transformation is:
\(f(x+5) \implies f(x) \: \textsf{translated}\:5\:\textsf{units left}\)
Question 11
\(\textsf{Parent function}: \quad f(x)=x^3\)
\(\textsf{Given function}: \quad f(x)=\left(\dfrac{1}{5}x\right)^3\)
Comparing the parent function with the given function, we can see that the x-value of the parent function has been multiplied by ¹/₅.
Therefore, the transformation is:
\(y=f\left(\dfrac{1}{5}x\right) \implies f(x) \: \textsf{stretched parallel to the x-axis (horizontally) by a factor of} \: \dfrac{1}{\frac{1}{5}}\)\(\textsf{As }\dfrac{1}{\frac{1}{5}}=5 \implies \textsf{horizontal stretch by a factor of 5}\)
Question 12
\(\textsf{Parent function}: \quad f(x)=x^3\)
\(\textsf{Given function}: \quad f(x)=(-x)^3\)
Comparing the parent function with the given function, we can see that the x-value of the parent function has been multiplied by -1.
Therefore, the transformation is:
\(y=f(-x) \implies f(x) \: \textsf{reflected in the} \: y \textsf{-axis}\)
Learn more about graph transformations here:
https://brainly.com/question/27845947
Find the focus.
x2 = 6y
A. (0, 3/2)
B. (0,6)
C. (0, -3/2)
D. (3/2,0)

Answers
Answer:
The answer would be (0,3/2) or letter A.
Step-by-step explanation:
In conclusion the answer is letter A (0,3/2)
You welcome.
The co-ordinate of the focus of the given equation of the parabola x^2=6y is (0,3/2).
We have given the equation is
\(x^2 = 6y\)
We know that the general equation of the parabola is,
\(x^2=4ay\)
A line that passes through the focus and divides the parabola into two halves is known as the axis of symmetry.
What are the coordinates of the focus?
The coordinates of the focus \(f(0, a)\)
We have to determine the value of
\(a4a=6a \implies 6/4a=3/2\)
Therefore the coordinate of the focus is\((0,3/2)\).
To learn more about the focus visit:
https://brainly.com/question/4148030
#SPJ2
A bag contains two red marbles, four green ones, one lavender one, two yellows, and two orange marbles. HINT [See Example 7.] How many sets of five marbles include either the lavender one or exactly one yellow one but not both colors?
Answers
There are 2518 sets of five marbles that include either the lavender one or exactly one yellow one, but not both.
To solve this problem, we need to find the number of sets of five marbles that include either the lavender one or exactly one yellow one, but not both colors. Here's one way to approach the problem:
Number of sets of five marbles that include the lavender one: There is only one lavender marble, so we can choose any 4 other marbles to go with it.
There are a total of 7 marbles to choose from, so there are 7 possible choices for the first marble, 6 for the second, 5 for the third, and 4 for the fourth.
This gives us a total of 7 x 6 x 5 x 4 = 840 possible sets of five marbles that include the lavender one.
Number of sets of five marbles that include exactly one yellow one: There are two yellow marbles,
So there are 2 possible choices for the yellow marble. For each choice, we can choose any 4 other marbles to go with it.
As before, there are 7 marbles to choose from, so there are 7 possible choices for the first marble, 6 for the second, 5 for the third, and 4 for the fourth.
This gives us a total of 2 x (7 x 6 x 5 x 4) = 1680 possible sets of five marbles that include exactly one yellow one.
Number of sets of five marbles that include both the lavender one and exactly one yellow one:
We need to subtract these sets from the total number of sets that include either the lavender one or exactly one yellow one.
We have already found that there are 840 sets of five marbles that include the lavender one, and 1680 that include exactly one yellow one.
To find the number of sets that include both, we can choose any one yellow marble and the lavender one.
There are 2 choices for the yellow marble and 1 choice for the lavender one,
So there are 2 x 1 = 2 possible sets of five marbles that include both the lavender one and exactly one yellow one.
Number of sets of five marbles that include either the lavender one or exactly one yellow one, but not both:
Finally, we need to subtract the number of sets that include both the lavender one and exactly one yellow one from the total number of sets that include either the lavender one or exactly one yellow one.
The total number of sets that include either the lavender one or exactly one yellow one is 840 + 1680 = 2520. The number of sets that include both is 2,
So the number of sets that include either the lavender one or exactly one yellow one, but not both, is 2520 - 2 = 2518.
For more questions on Permutation and Combination
https://brainly.com/question/1216161
#SPJ4
Consider this equation.
cos(0) = 4/41
If 0 is an angle in quadrant IV, what is the value of sin(0)
Answers
Answer: sin(0) = 40.804/41
Step-by-step explanation:

Make x the subject of m= n+ 1 + x/p
Answers
Answer:
Step-by-step explanation:
m = n + 1 + x/p
First, we can start by subtracting (n+1) from both sides:
m - (n+1) = x/p
Then, we can multiply both sides by p to isolate x:
p(m - (n+1)) = x
So the final answer is:
x = p(m - (n+1))
Look at the picture.
Thank u!

Answers
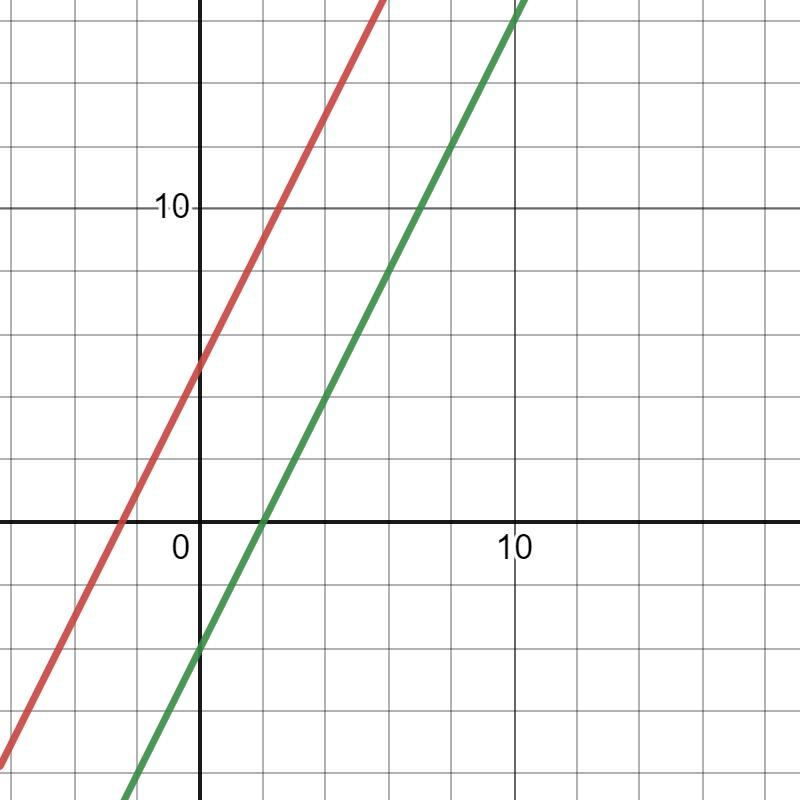
Given f(x)= 2x+5 and g(x)= (2x+5)-9, describe how the graph of g compares with the graph f.
Answers
The graph of both the Functions will be Parallel
What are Functions?
A function is an expression, rule, or law in mathematics that describes a connection between one variable (the independent variable) and another variable (the dependent variable).
Solution:
Please refer to the Graph attached
The graph of both the Functions will be Parallel
because, The Slope of both the functions is 2
To learn more about Functions from the given link
https://brainly.com/question/22340031
#SPJ1
ABC is a right angled triangle. if B = 90°, AC = 96 cm, C = 30°.
Answers
The length of side AB in right angled triangle ABC will be 48 cm.
What is a right angled triangle?Every triangle with one 90° angle is said to have a right angle. The triangle with a right angle is known as a right triangle because a right angle is 90 degrees.The longest side of a right angle is known as the hypotenuse, and it is opposite the right angle.
Given,
∠B= 90°, AC = 96 cm, ∠C = 30°
Now, we know, Trignometric ratio sin θ in triangle can be given by-:
sin θ = \(\frac{perpendicular}{hypotenuse}\)
From given figure,
Perpendicular= AB= ?
and Hypotenuse= AC = 96
and θ= 30°
Hence,
sin 30° =\(\frac{perpendicular}{hypotenuse}\)= \(\frac{AB}{96}\)
\(\frac{1}{2} = \frac{AB}{96}\) (∵ sin 30°= 1/2)
\(AB=\frac{96}{2}\)
\(AB= 48 cm\)
Thus, AB= 48 cm
Learn more about right angled triangle here:
https://brainly.com/question/3772264
#SPJ1
Correct Question:ABC is a right angled triangle. if B = 90°, AC = 96 cm, C = 30°. Find AB = ?

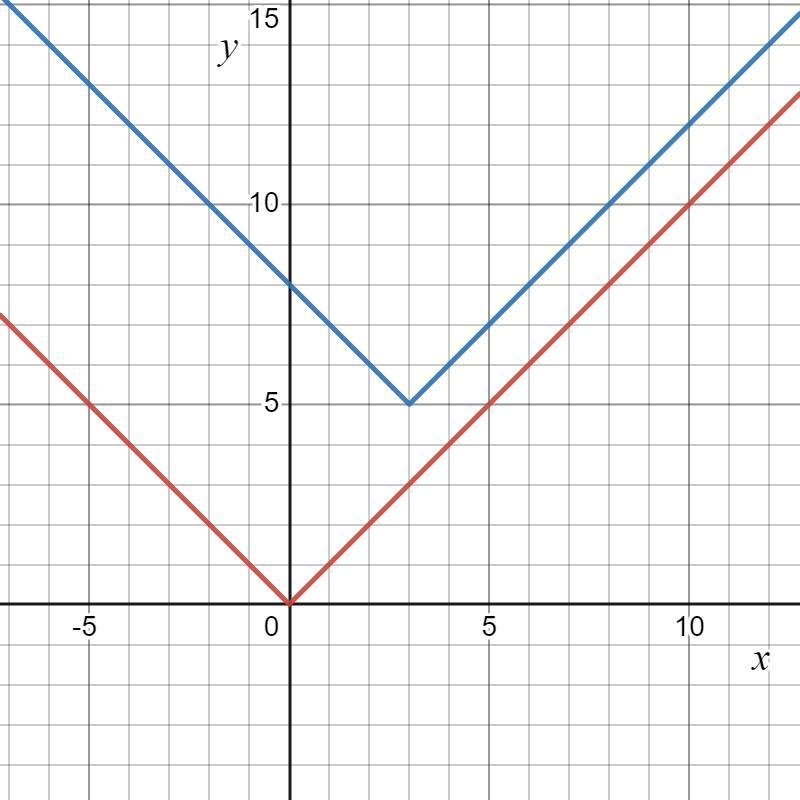
describe the transformations from the graph f(x)=|x| to the graph d(x) = -|x-3| + 5
Answers
The function d(x) = - |x - 3| + 5 is the result of using an horizontal translation, reflection about the x-axis and vertical translation on the function f(x) = |x|.
What kind of transformations are used to transform of the equation of a given graph?
In this question we have the definition of a function (f(x)) and its image (d(x)), the latter is the result of three rigid transformations:
Horizontal translation
f'(x) = f(x - 3)
Reflection about the x-axis
f''(x) = - f'(x)
Vertical translation
d(x) = f''(x) + 5
If we know that f(x) = |x|, then the series of rigid transformations is shown below:
Horizontal translation
f'(x) = |x - 3|
Reflection about the x-axis
f''(x) = - |x - 3|
Vertical translation
d(x) = - |x - 3| + 5
To learn more on rigid transformations: https://brainly.com/question/1761538
#SPJ1