41 = 5x + 35 and 3 = 4x + 10. Find the measure of x, 21 and 22.
1
2
3
4
6
5
8
7

Answers
Look : angle 1 + angle 3 = 180°
because it is a straight line.
Thus ;
\(5x + 35 + 4x + 10 = 180\)
Simplification
\(9x + 45 = 180\)
Subtract sides 45
\(9 x = 180 - 45\)
\(9x = 135\)
Divided sides 9
\( \frac{9}{9}x = \frac{135}{9} \\ \)
\(x = 15\)
So x = 15°
_________________________________
angle 1 = 5x + 35°
angle 1 = 5 ( 15 ) + 35°
angle 1 = 75° + 35°
angle 1 = 110°
_________________________________
angle 1 + angle 2 = 180°
110° + angle 2 = 180°
Subtract sides 110°
angle 2 = 180° - 110°
angle 2 = 70°
_________________________________
And we're done...♥️♥️♥️♥️♥️
Related Questions
If f(x)=-3x² +1, then which of the following is the value of f(-2)?
a) -11
b) 37
c) -35
d) -37
Answers
Answer:
A, -11
Step-by-step explanation:
f(x)=-3x(-2)+1
=-3(4)+1
=-12+1
=-11
Step-by-step explanation:
f(x)=3x²+1
f(-2)=3(-2)²+1
= -12+1
=-13 ans
Write the equation of the line in slope-intercept form (y=mx+b) for each of the following.
help ill brainlist

Answers
The linear equation that is modeled by the table is:
y = 2x + 1
How to write the linear equation?A general linear equation is written as:
y = a*x + b
Where a is the slope and b is the y-intercept.
If the line passes through two points (x1, y1) and (x2, y2), then the slope is:
a = (y2 - y1)/(x2 - x1)
Here we can use the first two points on the table (-3, -5) and (-1, -1), we will get the slope:
a = (-1 + 5)/(-1 + 3)
a = 4/2 = 2
Then the line is something like:
y = 2x + b
To find the value of b we can use one of the points (-3, -5), replacing these values we will get:
-5 = 2*-3 + b
-5 = -6 + b
-5 + 6 = b
1 = b
Then the linear equation is:
y = 2x + 1
Learn more about linear equations:
https://brainly.com/question/1884491
#SPJ1
Pls answer fast!!! Whoever gets it correct first gets a brainly!!!!

Answers
Answer: B
Step-by-step explanation:
The answer is 9x^2 + 14xy -19y^2
Qa.) State the contrapositive of the following implication. If G is a connected planar graph then G has at least one vertex of degree <= 5.
Qb.) Prove the contrapositive stated in part (a). Hint: use the fact that if G is a connected Planar graph , then e <= 3v-6.
Qc.) Use part (a) to show that every planar graph can be colored with 6 (or less) colors. Hint: Use a proof by Induction on the number of vertices G.
Answers
We assume that G is a connected planar graph with no vertex of degree <= 5. We will use e <= 3v - 6 to prove that G is not a planar graph. By handshaking lemma, we know that 2e = sum of degrees of all vertices. Let d be the maximum degree of G.
Qa. Contrapositive of an implication is a new implication formed by negating both the hypothesis and the conclusion.
The contrapositive of the implication "If G is a connected planar graph, then G has at least one vertex of degree <= 5" is "If G has no vertex of degree <= 5, then G is not a connected planar graph."
Qb. Proof: We assume that G is a connected planar graph with no vertex of degree <= 5.
We will use e <= 3v - 6 to prove that G is not a planar graph. By handshaking lemma, we know that 2e = sum of degrees of all vertices.
Let d be the maximum degree of G. Since G has no vertex of degree <= 5, then d >= 6.
Thus, the sum of degrees of all vertices in G is greater than or equal to 6v/2, which is equal to 3v.
Hence, 2e >= 3v.
Substituting this inequality in e <= 3v - 6, we get 2e >= 3e - 6, which implies that e >= 6.
Since e >= 6, it follows that G is not planar.
Qc. Proof: We use proof by induction on the number of vertices of G. For a graph with one vertex, the statement is trivially true.
For a graph with n > 1 vertices, assume that every planar graph with at most n - 1 vertices can be colored with 6 (or less) colors.
Let G be a planar graph with n vertices.
By part (a), there exists a vertex v of G with degree <= 5.
We remove v and all its edges from G to get a new graph G' with n - 1 vertices.
By the induction hypothesis, we can color G' with 6 (or less) colors.
We add back v and its edges to G.
Since v has degree <= 5, at most 5 colors are used on its adjacent vertices.
We use a new color for v.
Thus, G can be colored with 6 (or less) colors.
Therefore, by induction, the statement is true for all planar graphs.
To know more about planar graph visit: https://brainly.com/question/30954417.
#SPJ11
a child swim 25 yards in 12 seconds how many feet can he swim per second
Answers
Answer:
About 2 seconds
Step-by-step explanation:
25/12
2.0833333333333333333333333333333333333333333333333333333333333333................
if f(x) = -3x+4 and g(x) = 2, solve for the value of x for which f(x) = g(x) is true.
Answers
Answer:
x=1
Step-by-step explanation:
you have -3x+4 and your left with one whole number when you put -3 and 4 together
Yall can u help please?

Answers
The amount of money left with Dalton on gift card is given by the equation
9.95 + m = 25
Given data ,
Let the total amount of money on the gift card be = $ 25
Now , the amount of money spent on restaurant = $ 9.95
So , the amount of money left is
m = 25 - 9.95
On simplifying the equation , we get
m = $ 15.05
Hence , the amount left is m = $ 15.05
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
6. The difference between 2 number is 36.
The larger number is 4 times as great as the
smaller. What are the 2 numbers?
Answers
Answer: 48 and 12.
Step-by-step explanation:
Let the smaller number is x. Hence, the larger number is 4*x.
The difference between 2 number is 36.
So,
4*x-x=36
3*x=36\ |:3
x=12.
4*x=12*4
4*x=48.
Good luck an' have a nice day!
y = 3(4-2) + 5.5
rhhehrhrhrhrhrhrhrhrh
thrhththhththththtth
i have to somehow make this 20 characters long so
f
f
f
f
f
ff
f
f
f
f
f
Answers
Step-by-step explanation:
\(y = 3(4 - 2) + 5.5 \\ y = 3(2) + 5.5 \\ y = 11.5\)
Consider the relation given by the graph below.
a) Is the relation a function? Why or why not?
b) Determine the domain and range of the graph.

Answers
The given relation is function, because the curve of y = p(x) has its exist for every x in its domain(-6, 3) and the range of the function is lies between (-1, 9).
What are functions?
Functions is the relationship between sets of values. e g y=f(x), for every value of x there is its exists in set of y. x is independent while Y is dependent variable.
As Clearly the shows in the graph the structure is decreasing, increasing and then decreasing. And implies, curve is continuous in its limits and for every x (-6,3) there is exist in range of y(-1, 9).
Thus, The given relation is function, and domain is (-6, 3) and the range of the function is lies between (-1, 9).
learn more about function here:
brainly.com/question/21145944
#SPJ1
If the two spinners below are spun, what is the probability that the numbers will add to more than 4?
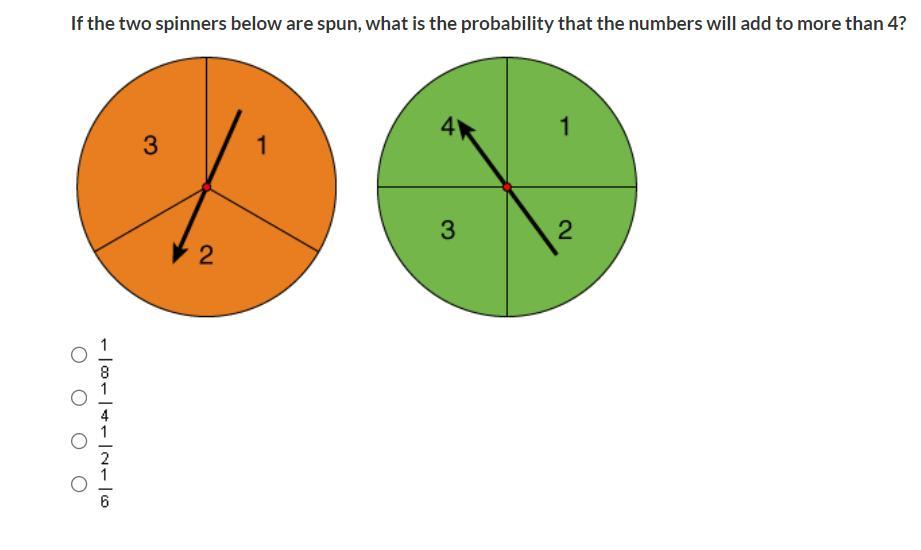
Answers
Answer: The answer is 1/4.
Step-by-step explanation:
I NEED AN ANSWER ASAP PLEASE

Answers
Step-by-step explanation:
the correct answer is option a 6a-7
A piece of aluminum with a mass of 100.0 g has a temperature of 20.0°C. It absorbs 1100 J of heat energy. What is the final temperature of the metal?
Answers
Answer:
31.81°CStep-by-step explanation:
Using the formula for calculating heat energy H = mcΔT
m = mass of the aluminum (in g/kg)
c = specific heat capacity of aluminum
ΔT = change in temperature = T - Ti (in °C)
T is the final temperature
Ti is the initial temperature
Given m = 100.0g, c = 0.931096J/g °C, Ti = 20°C, H = 1100J T = ?
Substituting the given values into the formula;
1100 = 100*0.931096 (T - 20)
1100 = 93.1096T - 1862.192
93.1096 T = 1100+1862.192
93.1096 T = 2962.192
T = 2962.192/93.1096
T = 31.81°C
The final temperature of the metal is 31.81°C
Answer:
31.81c
Step-by-step explanation:
1100 = 100*0.931096 (T - 20)
1100 = 93.1096T - 1862.192
93.1096 T = 1100+1862.192
93.1096 T = 2962.192
T = 2962.192/93.1096
T = 31.81°C
MT&A uses the function f(x)=475-15x-15x.to depreciate smart phones. where f represents the value of smart phone and x represents the number of months since its purchase. a) find f^-1 and explain what it represents in this situacions When will the deprecated value of smart phone be less than $100.00? what does x represent in f^-1(x) =30? What is the value of x? Graph f(x) and f^-1 (x) on the same coordinate
Answers
Answer:
Find the answers in the explanation
Step-by-step explanation:
The given function is
f(x)=475-15x
A.) To find f^-1 and explain what it represents in this situacions, let f(x) = y. That is,
Y = 475 - 15x
Interchange y and x and make y the subject of formula
X = 475 - 15y
-15y = x - 475
Y = 475/15 - x/15
Y = (475 - x) / 15
Therefore,
f^-1(x) = (475 - x) / 15
If the function depreciates the smartphone, then, the inverse function will appreciate it.
When will the deprecated value of smart phone be less than $100.00
Substitute 100 for f(x) and find x
100 = 475 - 15x
-15x = 100 - 475
-15x = - 375
X = 375/15
X = 25
Therefore, the deprecated value of smart phone be less than $100.00 in the next 26 months.
what does x represent in f^-1(x) =30?
X represent the number of months for the smartphone appreciations
What is the value of x?
Substitute the inverse function for 30 and make x the subject of formula in the equation
f^-1(x) = (475 - x) / 15
30 = (475 - x) / 15
Cross multiply
450 = 475 - x
X = 475 - 450
X = 25 months
Graph f(x) and f^-1 (x) on the same coordinate
It is known that lim 20 sin(2.c) 2x - 1. What is lim tan(2x) X+0 6x sec(3x) ? A 0 B 1 6 C 1 3 D nonexistent
Answers
The limit lim (tan(2x) / (6x sec(3x))) as x approaches 0 is 1/3, which corresponds to option C.
To find the limit lim (tan(2x) / (6x sec(3x))) as x approaches 0, we can use L'Hopital's rule, which states that if the limit of the ratio of two functions' derivatives exists, then that limit is equal to the limit of the ratio of the original functions.
First, let's find the derivatives of the numerator and denominator:
d(tan(2x))/dx = 2 * sec^2(2x)
d(6x sec(3x))/dx = 6 sec(3x) + 18x sec(3x) tan(3x)
Now, let's apply L'Hopital's rule and find the limit of the ratio of the derivatives as x approaches 0:
lim (2 * sec^2(2x) / (6 sec(3x) + 18x sec(3x) tan(3x))) as x -> 0
At x = 0, we have:
2 * sec^2(0) / (6 sec(0) + 0) = 2 * 1 / (6 * 1) = 2/6 = 1/3
So, the limit lim (tan(2x) / (6x sec(3x))) as x approaches 0 is 1/3, which corresponds to option C.
Learn more about limit:
https://brainly.com/question/12211820
#SPJ11
Here were 87 sunflowers at the flower shop in the morning. There were 56 sunflowers left at the end of the day. How many sunflowers were sold? Explain a way to solve the problem.
Answers
Answer:
31
Step-by-step explanation:
We just have to calculate 87 - 56 which is 31 so the answer is 31 sunflowers.
Answer:
31
Step-by-step explanation:
Since we know that we started with a higher number than we ended with, it is obvious that this is a subtraction problem. Then, we simply have to find the difference by subtracting 87 by 56 (87 - 56 = x). After the calculation, we see that the answer is 31 (87 - 56 = 31).
Write and equati9n of a l8ne that passes through (1,-2) and is perpendicular to -4x+7y=21
Answers
Given:
A line passes through (1,-2) and is perpendicular to \(-4x+7y=21\).
To find:
The equation of that line.
Solution:
We have, equation of perpendicular line.
\(-4x+7y=21\)
Slope of this line is
\(m_1=-\dfrac{\text{Coefficient of x}}{\text{Coefficient of y}}\)
\(m_1=-\dfrac{-4}{7}\)
\(m_1=\dfrac{4}{7}\)
Product of slope of two perpendicular lines is -1.
\(m_1\times m_2=-1\)
\(\dfrac{4}{7}\times m_2=-1\)
\(m_2=-\dfrac{7}{4}\)
Now, slope of required line is \(-\dfrac{7}{4}\) and it passes through (1,-2). So, the equation of line is
\(y-y_1=m(x-x_1)\)
where, m is slope.
\(y-(-2)=-\dfrac{7}{4}(x-1)\)
\(4(y+2)=-7(x-1)\)
\(4y+8=-7x+7\)
\(4y+7x=7-8\)
\(7x+4y=-1\)
Therefore, the equation of required line is \(7x+4y=-1\).
Tyler is overdrawn at the bank by $180. His brother owes $70 more than him. How much money does Tyler’s brother owe the bank? Is the $180 a positive or negative amount? Is the $70 a positive or negative amount
Answers
Answer:
Tyler owes $250 and both $180 and $70 are positive.
Step-by-step explanation:
Tyler owes $180.
Tyler's brother owes $70 more than him.
180 + 70 = 250
Tyler owes the bank $250.
What is the solution of the equation 3 and minus 2 is equal to 46?
Answers
The solution of the equation 3z minus 2 is equal to 46 is 16.
The given equation '3z minus 2 is equal to 46' can be written as
3z - 2 = 46
Now solving for z because the value of z will give the required solution of the given equation. So now finding the z from the equation:
3z = 46 + 2
3z = 48
z = 48/3
z = 16
The value of the z is 16 which represents the solution of the given equation i.e 3z minus 2 is equal to 46.
Therefore it is concluded that the solution of the equation 3z minus 2 is equal to 46 is 16.
You can learn more about equation at
https://brainly.com/question/22688504
#SPJ4
Why are factorial designs useful in testing theories?
a. They allow researchers to explore the construct validity of a theory.
b. Results from factorial designs are typically straightforward and easy to interpret.
c. They allow researchers to understand the nuances of how variables interact.
d. Results from factorial designs are always intuitive.
Answers
Factorial design are useful in testing theories because they enable researchers to investigate a theory's construct validity. so the correct answer is option (a).
What is factorial designs?A key technique for identifying the impact of numerous variables on a response is the factorial design. Traditionally, experiments are planned to ascertain how one variable affects just one response.
What is testing theories?The corpus of knowledge supporting the analysis and application of test results. The definition and measurement of reliability are of primary relevance. Classical test theory, generalizability theory, and item response theory are examples of theoretical frameworks.
a) They enable academics to investigate a theory's construct validity.
To know more about factorial design visit:
https://brainly.com/question/14053832
#SPJI
make y the subject in question 19

Answers
by solving this equation, the value of y = (x²+1)/(1-x²)
What do you mean by equation?Equation can be used to represent relationships between variables and to solve problems. They are written using an equal sign (=) and can include numbers, variables, and mathematical operations such as addition, subtraction, multiplication, and division.
To make y the subject of the equation x = √((y-1)/(y+1)),
x = √[(y-1)/(y+1)]
we can square both sides:
x² = (y-1)/(y+1)
Next, we can multiply both sides by (y+1) to get rid of the fraction:
x² × (y+1) = y-1
x²y + x² = y - 1
Rearranging the terms:
x² + 1 = y - x²y
x² + 1 = y(1 - x²)
Divide both side by (1-x²) we get
y = (x²+1)/(1-x²)
So, y is the subject of the equation is y = (x²+1)/(1-x²)
To know more about expression visit:
brainly.com/question/29176690
#SPJ1
what is the distance of KF. round to the nearest tenths

Answers
Answer:
its 9.2
Step-by-step explanation:
Well i counted 7 units (x-axis) and 6 units (y axis). 6 squared is 36 and 7 squared is 49. Add them together and get 85. Square root 85 and youll get 9.21954445729. Round it to the nearest tenths and get 9.2
Please help I'm stuck

Answers
Answer: Inequality notation is < or ≥.
Step-by-step explanation:
EQUATION ONE: -5x + 7 > 47, x < -8
EQUATION TWO: -5x + 7 ≤ -43, x ≥ 10

Twelve less than a number is 50.
Answers
Answer:
62
Step-by-step explanation:
another way to write this is
x - 12 = 50
the answer is 62
62 - 12 = 50
If sin θ = 45 4 5 and 2 π 2 < θ < 32 3 π 2 , what is the value of tan θ?
Answers
If sin θ = 45 4 5 and 2 π 2 < θ < 32 3 π 2 , the value of tan(θ) is 1125/sqrt(23).
How to find the value oftan(θ)First, we need to find the value of cos(θ) since we know sin(θ).
sin²(θ) + cos²(θ) = 1
cos²(θ) = 1 - sin²(θ)
cos(θ) = sqrt(1 - sin²(θ))
cos(θ) = sqrt(1 - (45/4)^2/5^2)
cos(θ) = sqrt(1 - (2025/1600))
cos(θ) = sqrt(575/1600)
cos(θ) = sqrt(23)/20
Now, we can find the value of tan(θ).
tan(θ) = sin(θ)/cos(θ)
tan(θ) = (45/4)/sqrt(23)/20
tan(θ) = (45/4) * (20/sqrt(23))
tan(θ) = (225/2) * (1/sqrt(23))
tan(θ) = (225/2) * (sqrt(23)/23)
tan(θ) = 1125/sqrt(23)
Therefore, the value of tan(θ) is 1125/sqrt(23).
Learn more about tan at https://brainly.com/question/16157693
#SPJ1
make k the subject of the formula h(k+6)=3h-k
Answers
Answer:
k = - \(\frac{3h}{h+1}\)
Step-by-step explanation:
Given
h(k + 6) = 3h - k ← distribute parenthesis on left side
hk + 6h = 3h - k ( add k to both sides )
hk + k + 6h = 3h ( subtract 6h from both sides )
hk + k = - 3h ← factor out k from each term on the left side
k(h + 1) = - 3h ( divide both sides by (h + 1) )
k = - \(\frac{3h}{h+1}\)
In the figure, a∥b and m∠3 = 34°.
What is the m∠7?
Enter your answer in the box. |__|
Answers
Therefore, In the figure, a∥b angle m∠7 = 34° .
What is angle ?An angle is a figure in Euclidean geometry made up of two rays that share a vertex, or common terminus, and are referred to as the sides of the angle. Angles of two rays lie in the plane containing the rays. Angles can also result from the intersection of two planes. Dihedral angles are the name given to them.
Here,
Given that a and b are parallel lines,
∠3 and ∠7 are corresponding angles and congruent
m∠3 = 34°
thus ,m∠7 =m∠3 = 34°
so, m∠7 = 34°
Therefore, In the figure, a∥b m∠7 = 34° .
To know more about angle , visit
https://brainly.com/question/28451077
#SPJ1
Find the domain of f(x) = -√√²-4.
Ox≥ 2 orx≤ - 2
Ο x >2
0x2 -2 or x ≤ 2
O all real numbers
Answers
The domain of the given function is x≤-2
What are functions?Function, in mathematics, is an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable).
Given here: The function f(x)=-√(√-4x)²
Simplifying the expression we get
f(x)=-√(√-4x)²
f(x)= -√-4x
Case 1) If the domain of x is greater than 2 then we have
f(3)=-√-12 which is a complex number and thus is not possible.
Case2 id x≤-2
then we have
f(-2)=-√8 which is not complex
Thus the feasible domain of the function is given by x≤-2
Learn more about functions here:
https://brainly.com/question/28303908
#SPJ1
If each 2 cm on the scale drawing equals 4 feet, what are the actual dimensions of the room? (5 points) a Length = 16 feet, width = 12 feet b Length = 10 feet, width = 8 feet c Length = 32 feet, width = 24 feet d Length = 14 feet, width = 12 feet
Answers
The correct option is C. Length = 24 feet, width = 18 feet
How to find the Length of a room?To measure a rectangular room, use a tape measure, pencil and paper to record the length and width of the room. Then multiply these numbers to get the total area of the room.
The calculation is as follows:
Since 2cm = 6 feet
So,
The length is = 4(6) = 24 feet
And, the width be = 3(6) = 18 feet
Read more about length and width here:
https://brainly.com/question/15161439
#SPJ1
A scale drawing of Julie's living room is shown below:
A rectangle is shown. The length of the rectangle is labeled as length equal to 8 cm, and the width is labeled as width equal to 6 cm.
If each 2 cm on the scale drawing equals 4 feet, what are the actual dimensions of the room?
A)Length = 16 feet, width = 12 feet
B)Length = 10 feet, width = 8 feet
C)Length = 32 feet, width = 24 feet
D)Length = 14 feet, width = 12 feet
which of the following situations describes the use of an atm? a. abby purchased an item and paid for it when the bill came in the mail.b. Abby wrote out an amount for an item and gaveit to a cashier.c. Abby entered a PIN to begin a transaction andreceived an amount of cash.d. Abby balanced her checkbook.
Answers
The situation that describes the use of an ATM is option C, where Abby entered a PIN to begin a transaction and received an amount of cash.
An ATM, or Automated Teller Machine, is a self-service banking machine that allows users to perform various financial transactions, including withdrawing cash, depositing money, checking account balances, and transferring funds. To use an ATM, the user typically needs to have a debit card or ATM card linked to their bank account, and they need to enter a unique Personal Identification Number (PIN) to access their account.
Once the user enters the correct PIN, they can choose the type of transaction they want to perform, such as withdrawing cash, and the machine dispenses the requested amount of cash.
Therefore, option C is the correct answer that describes the use of an ATM.
To know more about ATM click on below link :
https://brainly.com/question/24198010#
#SPJ11