4) You randomly select one card from a​ 52-card deck. Find the probability of selecting the 6 of hearts or the ace of diamonds.

Answer:

See explanation

Step-by-step explanation:

The question is incomplete, as the coordinate of A is not given.

However, the rule to follow has been stated in the question.

i.e.

\((x,y) \to (-x,y)\)

Assume that:

\(A = (2,5)\)

After reflection, A will be:

\(A =(-2,5)\)

Answer:

C.

Step-by-step explanation:

because x value cannot be repeated in an ordered pair

Answer:

The area of this triangle is (1/2)(9)(8) = 36.

Answer:

The girls collected 182 pounds of rocks more the second weekend of hiking compared to the first weekend of hiking.

Step-by-step explanation:

312 + 234 = 546

615 + 113 = 728

728 - 546 = 182

182 lbs

To calculate Swornima's annual income and the amount of tax she should pay, let's break down the information provided:

Monthly basic salary: Rs 48,000

Social security tax rate: 1%

Income tax rate on income up to Rs 5,00,000: 0% (no tax)

Income tax rate on income from Rs 5,00,001 to Rs 7,00,000: 10%

Dashain allowance: 1 month's salary

Deposit in Citizen Investment Trust (CIT): 10%

Rebate on income tax: 10%

(i) Annual Income:

Swornima's monthly basic salary is Rs 48,000, so her annual basic salary would be:

Annual Basic Salary = Monthly Basic Salary x 12

= Rs 48,000 x 12

= Rs 5,76,000

Additionally, she receives 1 month's salary as the Dashain allowance, which we can add to her annual income:

Annual Income = Annual Basic Salary + Dashain Allowance

= Rs 5,76,000 + Rs 48,000

= Rs 6,24,000

Swornima's annual income is Rs 6,24,000.

(ii) Tax Rebate:

Swornima receives a 10% rebate on her income tax. To calculate the rebate, we need to determine her income tax first.

(iii) Annual Income Tax:

First, let's calculate the income tax for the range of income from Rs 5,00,001 to Rs 7,00,000. The tax rate for this range is 10%.

Taxable Income in this range = Rs 6,24,000 - Rs 5,00,000

= Rs 1,24,000

Income Tax in this range = Taxable Income x Tax Rate

= Rs 1,24,000 x 0.1

= Rs 12,400

Now, let's calculate the total annual income tax:

Total Annual Income Tax = Income Tax in the range Rs 5,00,001 to Rs 7,00,000

= Rs 12,400

Next, we calculate the rebate on income tax:

Tax Rebate = Total Annual Income Tax x Rebate Rate

= Rs 12,400 x 0.1

= Rs 1,240

Swornima's annual income tax is Rs 12,400, and she receives a tax rebate of Rs 1,240.

To summarize:

(i) Swornima's annual income is Rs 6,24,000.

(ii) Swornima's tax rebate is Rs 1,240.

(iii) Swornima should pay an annual income tax of R

She increases her speed for 20 seconds:

She slows down for 10 seconds:

She stays approximately the same speed for the next 20 seconds:

She then slows down to a stop for the last 5 seconds.

The graph which represents the polar curve r = -4 sin ( 3θ ) is plotted

Polar coordinates describe the position of a point P in the plane by its separation from the origin, r, and the angle formed between the positive x-axis and the line segment leading to P.

To graph the polar curve, we make use of the following representations:

r represents the y-axis

θ represents the x-axis

Polar coordinates can also be extended into three dimensions using the coordinates (ρ, φ, θ), where ρ is the distance from the pole, φ is the angle from the z-axis ( called the co-latitude or zenith and measured from 0 to 180° ) and θ is the angle from the x-axis ( as in the polar coordinates ).

Given data ,

Let the polar curve be represented as A

Now , the polar coordinates is given as

r = -4 sin ( 3θ )

And , To graph the polar curve, we make use of the following representations:

r represents the y-axis

θ represents the x-axis

So , on simplifying , we get

The graph which represents the polar curve r = -4 sin ( 3θ ) is plotted

Hence , the polar curve is r = -4 sin ( 3θ )

To learn more about polar coordinates click :

https://brainly.com/question/26193139

#SPJ1

Answer:

D

Step-by-step explanation:

Answer:

The mean is 7 and the range is 5

Step-by-step explanation:

To find the mean, just add up the scores and divide the total by the number of scores.

To find the range, subtract the lowest value from the highest value.

Answer:

b)480 cm^2

Step-by-step explanation:

perimeter=(16+12+20) cm

=48 cm

lateral surface area= perimeter × height

=48×10 =480 cm^2

The solution is:  the rate of change is 3.

Here, we have,

Since the graph of f(x) is translated 1 unit down, we need to decrease the value of f(x) by 1 to find g(x):

g(x) = f(x) - 1

f(x) = 3|x| – 4

so, we get,

g(x) = 3|x| – 4 - 1

      = 3|x| – 5

Now, to calculate the rate of change over the interval 2 <= x <= 5, we can use the formula below:

rate = g(5) - g(2)/ 5-2

so, we get,

rate = 9/3 = 3

Therefore the rate of change is 3.

To learn more on subtraction click:

brainly.com/question/2346316

#SPJ1

Answer:

Graph 2

Step-by-step explanation:

See image attached. Hope this helps.

The second graph shown the polar curve at r = 7.

Given ,

Equation of polar curve = r = 2 + 5sin(θ)

We have to find ,

Which of following graph show polar curve ,

At  r = 2 + 5sin(θ)

The area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas.

First graph ;  r = 2 + 5sin(θ)

Where ,

\(\theta = 0\)

r = 2 + 5sin0

r = 2 + 5 (0)

r = 2

Second graph : r = 2 + 5sin(θ)

Where

\(\theta = \frac{\pi }{2}\)

Then,

r = 2 + sin\(\frac{\pi }{2}\)

r = 2 +5 ( 1 )

r = 2+5

r = 7

Third graph ;  r = 2 + 5sin(θ)

where

\(\theta = \pi\)

Then,

r = 2 + 5sin\(\pi\)

r = 2 + 5(0)

r = 2

Fourth graph ; r = 2 + 5sin(θ)

Where

r = 2 + 5sin\(\frac{3\pi }{2}\)

r = 2 + 5 (-1)

r = -3

Fifth graph ; r = 2 + 5sin(θ)

Where

\(\theta = 2\pi\)

r = 2 + 5sin(2π)

r = 2+ 5 (0)

r = 2

Comparing all the value of the graph ,the second graph shown the polar curve at r = 7.

Hence, The second graph shown the polar curve at r = 7.

For more information about Polar curves click the link given below.

https://brainly.com/question/1094340

The amount of interest owed will be $564.16.

Continuous compounding means process of calculating interest and reinvesting them into an account's balance over  infinite number of periods.

To get the interest owed, we will use the formula for compound interest which is \(A = P * e^{rt}\)

Given values:

P = $3,200

r = 12.99% = 0.1299

t = 15 = 15/12 = 1.25

Substituting the values

\(A = $3,200 * e^{0.1299 * 1.25}\\A = $3,200 * 1.1763012716\\A = 3764.16406912\\A = $3764.16\)

Interest owed = $3,764.16 - $3,200

Interest owed = $564.16

Read more about compounded interest

brainly.com/question/24274034

#SPJ1

Answer:

i think its 1.2 dollors im not 100 percent sure

Step-by-step explanation:

Answer:

it was a 2 year loan with $210 contributed each year

Step-by-step explanation:

Answer: C

Step-by-step explanation:

The rest of the quadrilaterals provided have 2 pairs of parallel lines.

The choice is:

Explanation:

The quadrilateral that has exactly one pair of parallel lines is called a trapezoid.

Here's what a trapezoid looks like :

\(\setlength{\unitlength}{1 cm}\begin{picture}(0,0)\linethickness{0.3mm}\qbezier(0,0)(0,0)(1,3)\qbezier(5,0)(5,0)(4,3)\qbezier(1,3)(1,3)(4,3)\qbezier(3,0)(8.2,0)(0,0)\put(-0.5,-0.3){$\sf A$}\put(5.3,-0.3){$\sf B$}\put(4.2,3.1){$\sf C$}\put(0.6,3.1){$\sf D$}\end{picture}\)

Let [r, s] denote the least common multiple of positive integers r and s. Find the number of ordered triples (a, b, c) of positive integers for which [a, b] = 1000, [b, c] = 2000, and [c, a] = 2000.

Solution 1

It's clear that we must have a = 2^j5^k, b = 2^m^6 and c = 2^p5^q for some nonnegative integers j, k, m, n, p, q. Dealing first with the powers of 2: from the given conditions, max(j, m)=3, max(m, p) = max(p, j) = 4. Thus we must have p = 4 and at least one of m, j equal to 3. This gives 7 possible triples (j,m,p): (0, 3, 4), (1, 3, 4), (2, 3, 4), (3, 3, 4), (3, 2, 4), (3, 1, 4) and (3, 0, 4).

Now, for the powers of 5: we have max (k, n) = max(n, q) = max(q, k) = 3. Thus, at least two of k, n, g must be equal to 3, and the other can take any value between 0 and 3. This gives us a total of 10 possible triples: (3, 3, 3) and three possibilities of each of the forms (3, 3, n), (3, n, 3) and (n, 3, 3).

Since the exponents of 2 and 5 must satisfy these conditions independently, we have a total of 7. 10= 70 possible valid triples.

Solution 2

1000=2³5³ and 2000= 2⁴5³. By looking at the prime factorization of 2000, c must have a factor of 2¹. If c has a factor of 53, then there are two cases: either (1) a or b = 5³2³, or (2) one of a and has a factor of 5³ and the other a factor of 2³. For case 1, the other number will be in the form of 2^x5^y, so there are 4 4 16 possible such numbers; since this can be either a orb there are a total of 2(16)-1=31 possibilities. For case 2, a and b are in the form of 2³5^x and 2^y5³, with a x<3 and y<3 (if they were equal to 3, it would overlap with case 1). Thus, there are 2(3-3)= 18 cases.

If c does not have a factor of 5³, then at least one of a and b must be 2³5³, and both must have a factor of 5³. Then, there are 4 solutions possible just considering a = 2353, and a total of 4.2-17 possibilities. Multiplying by three, as 0<=c<=2, there are 7.3 = 21.

Together, that makes 31 +18+21= 70 solutions for (a, b, c).

Learn more about integers at https://brainly.com/question/15276410.

#SPJ4

Answer:

x^2 - 4x + 4 = 0

x = 2

Step-by-step explanation:

(x - 2)(x - 2) = 0

x^2 - 2x - 2x + 4 = 0

x^2 - 4x + 4 = 0

The equation is:

x^2 - 4x + 4 = 0

It is a quadratic equation because of the x^2 term.

Now we solve it by factoring.

x^2 - 4x + 4 = 0

(x - 2)(x - 2) = 0

x - 2 = 0 or x - 2 = 0

x = 2 or x = 2

The only solution is x = 2.

Answer:

QS ≅ TR

Step-by-step explanation:

QS and TR are diagonals.

Diagonals are equal in both rectangle as well as parallelogram.

Answer:

- 4

Step-by-step explanation:

Step 1:

4 ( 2 - w ) + w = 20           Equation

Step 2:

8 - 4w + w = 20       Multiply

Step 3:

8 - 3w = 20       Combine Like Terms

Step 4:

- 3w = 12     Subtract 8 on both sides

Answer:

w = - 4

Hope This Helps :)

Answer:

w = -4

Step-by-step explanation:

4(2 - W) + w = 20

Distribute:          

8 - 4w + w = 20

Subtract 8 from both sides:

-4w + w = 12

Simplify:

-3w = 12

Divide:

w = -4

Double check your work by substitution:

4(2 - W) + w = 20

4(2 - (-4)) + (-4) = 20

4(6) + (-4) = 20

24 + (-4)= 20

20 = 20

Since we know that 20 does equal 20, we can conclude that the final answer is:

w = -4

Answer:

For the graph see attached image.

The y-intercept is 2

Step-by-step explanation:

The requested graph of the function is included in the attached image.

The y-intercept can be seen from the image, but also from finding the y-value when x= 0 (zero):

\(y=2\,\,\,3^x\\y=2\,\,\,3^0\\y = 2 \,\,\,(1)\\y = 2\)

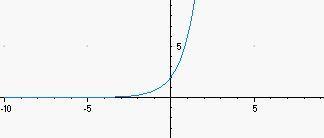
Answer:

To graph the function y = 2 • 3^x, we can start by identifying the y-intercept. The y-intercept is the point where the graph intersects the y-axis, which occurs when x = 0.

To find the y-intercept, we substitute x = 0 into the equation y = 2 • 3^x:

y = 2 • 3^0 = 2 • 1 = 2

Therefore, the y-intercept is 2, which corresponds to option (B).

The temperature at 8:00 A.M. was 15°C.

Using the given information:
1. At 7:00 P.M., the temperature was 16°C.
2. This temperature was 9°C less than the temperature at 2:00 P.M.

We can use this information to find the temperature at 2:00 P.M.:
Temperature at 2:00 P.M. = 16°C (temperature at 7:00 P.M.) + 9°C
Temperature at 2:00 P.M. = 25°C

3. The temperature at 2:00 P.M. was 10°C higher than the temperature at 8:00 A.M.

Now, we can find the temperature at 8:00 A.M.:
Temperature at 8:00 A.M. = 25°C (temperature at 2:00 P.M.) - 10°C
Temperature at 8:00 A.M. = 15°C

To know more about temperature refer to

https://brainly.com/question/24746268

The property illustrated in equation 4(-8+5) = -32 + 20 is the Distributive Property.

The Distributive Property states that when a number is multiplied by a sum or difference in parentheses, it can be distributed or multiplied by each term inside the parentheses separately, and then the results can be added or subtracted.

In this case, the number 4 is multiplied by the sum (-8 + 5). By applying the Distributive Property, we distribute the 4 to each term inside the parentheses:

4(-8 + 5) = (4 * -8) + (4 * 5)

This simplifies to:

4(-8 + 5) = -32 + 20

Finally, we can perform the addition:

-32 + 20 = -12

Therefore, the equation demonstrates the application of the Distributive Property.

know more about Distributive Property here:

https://brainly.com/question/2807928

#SPJ8

Answer:

Length and Width = 10ft

Height = 5ft

Surface Area = 300 square feet

Step-by-step explanation:

Given

\(V = 500ft^3\) -- Volume

Let:

\(L = Length\)

\(W =Width\)

\(H = Height\)

Volume (V) is calculated as:

\(V = L * W * H\)

Substitute 500 for V

\(500 = L * W * H\)

Make H the subject

\(H = \frac{500}{LW}\)

The tank has no top. So, the surface area (S) is:  

\(S = L * W + 2*H*L + 2*H*W\)

\(S = L * W + 2H(L + W)\)

Substitute 500/LW for H

\(S = L * W + 2*\frac{500}{LW}(L + W)\)

\(S = L * W + \frac{1000}{LW}(L + W)\)

\(S = L W + \frac{1000}{L} + \frac{1000}{W}\)

Differentiate with respect to L and to W

\(S'(W) = L - \frac{1000}{W^2}\)

and

\(S'(L) = W - \frac{1000}{L^2}\)

Equate both to get the critical value

\(S'(W) = L - \frac{1000}{W^2}\)and \(S'(L) = W - \frac{1000}{L^2}\)

\(0 = L - \frac{1000}{W^2}\) and \(0 = W - \frac{1000}{L^2}\)

\(\frac{1000}{W^2} = L\) and \(\frac{1000}{L^2} = W\)

\(W^2L = 1000\) and \(L^2W = 1000\)

Make L the subject in  \(W^2L = 1000\)

\(L = \frac{1000}{W^2}\)

Substitute \(\frac{1000}{W^2}\) for L in \(L^2W = 1000\)

\((\frac{1000}{W^2})^2 * W = 1000\)

\(\frac{1000000}{W^4} * W = 1000\)

\(\frac{1000000}{W^3} = 1000\)

Cross Multiply

\(1000000 = 1000W^3\)

Divide both sides by 1000

\(1000 = W^3\)

Take cube roots of both sides

\(\sqrt[3]{1000} = W\)

\(10 = W\)

\(W = 10\)

Substitute 10 for W in \(L = \frac{1000}{W^2}\)

\(L = \frac{1000}{10^2}\)

\(L = \frac{1000}{100}\)

\(L = 10\)

Recall that:\(H = \frac{500}{LW}\)

\(H = \frac{500}{10*10}\)

\(H = \frac{500}{100}\)

\(H = 5\)

So, the dimensions are:

\(L, W=10\) and \(H = 5\)

The surface area is:

\(S = L * W + 2H(L + W)\)

\(S = 10*10 +2*5(10+10)\)

\(S = 10*10 +2*5*20\)

\(S = 100 + 200\)

\(S = 300\)

The volume comparison of the given data is written below:

In three dimensions, everything takes up some space. What is being measured here is the area's volume. The volume of an object is the area occupied inside its three-dimensional boundaries. It is referred to as the object's capability on occasion.

Given, The height of the cone and cylinder is twice the radius, while the radius of a sphere is the same.

The volume of the cone =   πr²h

Since, h = 2r

The volume of the cone =   πr² * 2r = 2/3 πr³

The volume of the Cylinder = πr²h

Since, h = 2r

The volume of the Cylinder = πr² * 2r = 2πr³

The volume of the sphere = 4 πr³

Thus, the volume of 3 cones = 2πr³

that is also equal to The volume of one Cylinder.

Thus, the volume of 2 cones = 4/3πr³

that is also equal to The 1/3 volume of the Cylinder.

Thus, the volume of 1 sphere = 4πr³

that is also equal to The volume of 2 cylinders.

Thus, the volume of 1 cone = 2/3πr³

that is also equal to The 1/6 volume of the cone.

Learn more about volume here:

brainly.com/question/13338592

#SPJ2

Answer: To find a vector perpendicular to the triangle, you can use the cross product of two vectors formed by subtracting two of the triangle's vertices. Specifically, if two vectors v1 and v2 are formed by subtracting one vertex from the other two, then their cross product v1 × v2 will be perpendicular to both v1 and v2, and therefore perpendicular to the triangle they form.

Mathematically, the cross product of two vectors in three-dimensional space is defined as:

v1 × v2 = ⟨y1z2 − z1y2, z1x2 − x1z2, x1y2 − y1x2⟩

So, to find a vector perpendicular to the triangle with vertices (x1,y1,z1), (x2,y2,z2), and (x3,y3,z3), you can choose any two vertices and compute their difference to get two vectors, and then take their cross product. For example, you could choose:

v1 = ⟨x2−x1,y2−y1,z2−z1⟩

v2 = ⟨x3−x1,y3−y1,z3−z1⟩

And then compute their cross product:

v1 × v2 = ⟨(y2−y1)(z3−z1) − (z2−z1)(y3−y1), (z2−z1)(x3−x1) − (x2−x1)(z3−z1), (x2−x1)(y3−y1) − (y2−y1)(x3−x1)⟩

This will give you a vector that is perpendicular to the triangle.

Step-by-step explanation:

Answer:

Average rate of change of the function will be = (-1.5)

Step-by-step explanation:

Average rate of change of a function f(x) is determined by the formula,

Average rate of change = \(\frac{f(b)-f(a)}{b-a}\) If a < x < b

We have to find the average rate of change of a function g(t) between the interval [-3, 1]

From the given table,

For t = -3,

g(-3) = 6

For t = 1,

g(1) = 0

Therefore, average rate of change of the function in the given interval

= \(\frac{g(1)-g(-3)}{1-(-3)}\)

= \(\frac{0-6}{1+3}\)

= \(-\frac{3}{2}\)

= - 1.5

Rounding to the nearest hundredth, the area is approximately 151.976 cm².

The formula for the area of a sector is:

A = (θ/360) x πr²

where θ is the central angle in degrees, r is the radius, and π is pi (3.14).

Plugging in the given values, we get:

A = (144/360) x 3.14 x 11^2

A = 0.4 x 3.14 x 121

A = 151.976

To learn more about the area;

https://brainly.com/question/27683633

#SPJ1

Answer:-1

Step-by-step explanation:f(x)=3-x2

This is also...

f(x)=3+[(-1)(x2)]

We will execute the exponential. Then, we will multiply the result by the coefficient of -1.

f(-2)=3-(-2)2

f(-2)=3-(+4)

f(-2)=3-4

f(-2)=-1