4. State all reasons why Rolle's Theorem does not apply to the function on the interval (– 2,0]. (2 points) 4. 2 f(x) = (x+1) 3. Find the absolute maximum and the absolute minimum off on the given interval. (2 points) f(x) = x + sin x ; [0,21] = 3.
Answers
Absolute minimum: f(pi) ≈ 3.14
Therefore, the absolute maximum of f(x) on [0,21] is approximately 21.82 and the absolute minimum is approximately 3.14.
For question 4, to apply Rolle's Theorem, a function must be continuous on a closed interval and differentiable on the open interval within that closed interval. However, for the function f(x) = (x+1)^2 on the interval (-2,0], the function is not differentiable at x = -1 because the derivative from the left side (-2, -1) is -2 and the derivative from the right side (-1,0] is 2. Therefore, Rolle's Theorem cannot be applied to this function on the given interval.
For question 3, to find the absolute maximum and minimum of the function f(x) = x + sin(x) on the interval [0,21], we first find the critical points by setting the derivative equal to zero:
f'(x) = 1 + cos(x) = 0
cos(x) = -1
x = pi
So, the critical point is at x = pi. We also need to check the endpoints of the interval:
f(0) = 0 + sin(0) = 0
f(21) = 21 + sin(21) ≈ 21.82
Now, we compare the values at the critical point and endpoints to find the absolute maximum and minimum:
f(pi) = pi + sin(pi) = pi ≈ 3.14
Absolute maximum: f(21) ≈ 21.82
Absolute minimum: f(pi) ≈ 3.14
Therefore, the absolute maximum of f(x) on [0,21] is approximately 21.82 and the absolute minimum is approximately 3.14.
Learn more about critical point here:
https://brainly.com/question/31017064
#SPJ11
Related Questions
About 50% of the people surveyed in a certain county work for a small business. A random number generator was used to simulate the results of the next four people surveyed.
The number 0 to 4 represent people who work for a small business, and the numbers 5 to 9 represent people who do not work for a small business.
Based on the simulated results shown below, what is the probability that at least one of the next four people surveyed works for a small business?
*
Answers
The probability that at least one of the next four people surveyed works for a small business is 0.9375 or 93.75%.
To determine the probability that at least one of the next four people surveyed works for a small business, we can first examine the possible outcomes of the random number generator for each person surveyed.
Since 50% of the people surveyed work for a small business, we can assign the numbers 0 to 4 to represent those who work for a small business, and the numbers 5 to 9 to represent those who do not work for a small business.
Now, let's look at the simulated results:
Person 1: 8 (does not work for a small business)
Person 2: 1 (works for a small business)
Person 3: 7 (does not work for a small business)
Person 4: 3 (works for a small business)
Out of the four people surveyed, two work for a small business (person 2 and person 4) and two do not work for a small business (person 1 and person 3).
To calculate the probability that at least one of the next four people surveyed works for a small business, we can use the complementary probability. That is, the probability that none of the next four people surveyed work for a small business is:
(5/10) * (5/10) * (5/10) * (5/10) = 0.0625
Therefore, the probability that at least one of the next four people surveyed works for a small business is:
1 - 0.0625 = 0.9375
To learn more about probability click on,
https://brainly.com/question/29588004
#SPJ4
Which expression is equivalent to (9c) (7c8) ?
16c
16c8
63c9
63c8
Answers
The correct answer is 63c9. To simplify the expression (9c) (7c8), we need to multiply the coefficients (numbers) and combine the variables with the same base.
In this case, we have:
(9c) (7c8) = 9 * 7 * c * c8
Multiplying the coefficients gives us 9 * 7 = 63.
Multiplying the variables with the same base, 'c' in this case, means adding their exponents. Here, we have c * c8, which equals c^(1+8) = c^9.
Putting it all together, (9c) (7c8) simplifies to 63c^9.
Therefore, the expression equivalent to (9c) (7c8) is 63c^9.
So, the correct answer is 63c9.
Learn more about expression here:
https://brainly.com/question/28170201
#SPJ11
(Brainliest if fast and correct)
The ages of three friends are consecutively one year apart. Together, their ages total 54 years. Which equation can be used to find
the age of each friend (where represents the age of the youngest friend)?
X=__
Answers
hope it helped jwgwhwfhwgwjwh

Answer:
21
Step-by-step explanation:
I took the k12 quiz
ON SATURDAY MORNINGS FROM 9:00 UNTIL NOON, BRENT WATCHES A GROUP OF PRESCHOOLERS WHILE THEIR PARENTS WORK OUT IN THE GYM. BRENT EARNS $7.25 PER HOUR PLUS $1.00 PER CHILD. TODAY THERE ARE 7 CHILDREN…HOW MUCH WILL BRENT EARN? SHOW YOUR WORK IN THE SOLUTION BOX AND CIRCLE YOUR FINAL ANSWER. PLACE IN THE BASKET WHEN FINISHED.
Answers
After conducting some mathematical operations, we know that Brent earned $28.75.
What are mathematical operations??A mathematical function known as an operation converts zero or more input values into a precisely defined output value.The quantity of operands affects the operation's arity.The order of operations refers to the rules that define the sequence in which we should perform the operations necessary to solve an expression.Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction are all referred to as PEMDAS (from left to right).So, the amount Brent will earn when there are 7 children:
Brent earns $7.25 per hour and he watched kids from 9:00 am to noon which is 3 hours.
$7.25 × 3 = $21.75He earns $1 per child and there are 7 children present, then:
7 × 1 = $7Total amount he earned: $21.75 + $7 = $28.75
Therefore, after conducting some mathematical operations, we know that Brent earned $28.75.
Know more about mathematical operations here:
brainly.com/question/20628271
#SPJ13
The correct question is given below;
ON SATURDAY MORNINGS FROM 9:00 UNTIL NOON, BRENT WATCHES A GROUP OF PRESCHOOLERS WHILE THEIR PARENTS WORK OUT IN THE GYM. BRENT EARNS $7.25 PER HOUR PLUS $1.00 PER CHILD. TODAY THERE ARE 7 CHILDREN…HOW MUCH WILL BRENT EARN?
Can someone help me please

Answers
Answer:
0.19 50% 15/20 9/10 95%
Step-by-step explanation:
I know
Calculate the 90% confidence interval for the following sample Sample: 7.9, 8.3, 8.4, 9.6, 7.7, 8.1, 6.8, 7.5, 8.6, 8, 7.8,7.4, 8.4, 8.9, 8.5, 9.4, 6.9,7.7. Assume normality of the data.
Answers
The 90% confidence interval for the given sample is (7.58, 8.60).
To calculate the 90% confidence interval for the given sample assuming normality of the data, we need to use the formula as follows;Confidence interval = X ± Z α/2(σ/√n)Where, X is the sample meanZ α/2 is the Z-score for the desired level of confidenceσ is the population standard deviationn is the sample sizeFirst, we need to calculate the sample mean and standard deviation.Sample mean,
X= (7.9 + 8.3 + 8.4 + 9.6 + 7.7 + 8.1 + 6.8 + 7.5 + 8.6 + 8 + 7.8 + 7.4 + 8.4 + 8.9 + 8.5 + 9.4 + 6.9 + 7.7) / 18
= 8.09
Sample standard deviation,
σ = √[Σ(xi - X)² / (n - 1)]σ = √[(7.9 - 8.09)² + (8.3 - 8.09)² + (8.4 - 8.09)² + (9.6 - 8.09)² + (7.7 - 8.09)² + (8.1 - 8.09)² + (6.8 - 8.09)² + (7.5 - 8.09)² + (8.6 - 8.09)² + (8 - 8.09)² + (7.8 - 8.09)² + (7.4 - 8.09)² + (8.4 - 8.09)² + (8.9 - 8.09)² + (8.5 - 8.09)² + (9.4 - 8.09)² + (6.9 - 8.09)² + (7.7 - 8.09)² / (18 - 1)]σ = 0.761
Now, we need to find the Z α/2 value from the standard normal distribution table.
Z α/2 = 1.645 (for 90% confidence level)Putting the values in the formula,Confidence interval =
X ± Z α/2(σ/√n)
= 8.09 ± 1.645(0.761/√18)
= 8.09 ± 0.511
= (8.09 - 0.511, 8.09 + 0.511)
= (7.58, 8.60).
To know more about confidence interval :
https://brainly.com/question/32546207
#SPJ11
Holler sold 150 frozen yogurts. Out of these frozen yogurts sold, 40% included toppings. How many frozen yogurts included toppings?
Answers
write the factors of the following expression x3 (2a‐6)+x2 (2a-6)
Answers
Given:
The expression is
\(x^3(2x-6)+x^2(2x-6)\)
To find:
The factors of the given expression.
Solution:
We have,
\(x^3(2x-6)+x^2(2x-6)\)
First taking \((2x-6)\) common, the given expression can be written as
\(=(2x-6)(x^3+x^2)\)
Taking \(x^2\) common from \((x^3+x^2)\), we get
\(=x^2(2x-6)(x+1)\)
Therefore, the factors of the given expression are \(x^2(2x-6)(x+1)\).
verify the identity by converting the left side into sines and cosines. (simplify at each step.) 8 cot(x) sec(x) = 8 csc(x) − 8 sin(x)
Answers
8 cot(x) sec(x) can be simplified to 8 csc(x) - 8 sin(x) by converting the left side into sines and cosines.
How can the expression 8 cot(x) sec(x) be simplified using trigonometric identities?
To verify the identity by converting the left side into sines and cosines, we'll simplify each step.
Starting with the left side of the equation:
8 cot(x) sec(x)
First, let's express cot(x) and sec(x) in terms of sines and cosines:
cot(x) = cos(x) / sin(x)
sec(x) = 1 / cos(x)
Substituting these values back into the equation:
8 (cos(x) / sin(x)) (1 / cos(x))
Next, we can cancel out the common terms of cos(x):
8 (1 / sin(x))
Finally, we can rewrite 1 / sin(x) as csc(x):
8 csc(x)
Therefore, the left side of the equation simplifies to 8 csc(x).
The right side of the equation is already in the desired form:
8 csc(x) - 8 sin(x)
Thus, we have successfully shown that the left side of the equation, after converting to sines and cosines, simplifies to the right side of the equation. The identity is verified.
Learn more about sines and cosines,
brainly.com/question/31129851
#SPJ11
1-4
please, thank you in advance!
1. 3. e-x (1+e- (1+e-x)2 dx 4 √2 (3x-1)³ dx 4 2. 4. 10³dx x²+3x-5 (x+2)²(x-1) dx
Answers
For question 1, we are asked to solve the integral 3e^-x(1+e^-(1+e^-x)^2)dx. This integral requires substitution, where u=1+e^-x and du=-e^-x dx. After substituting, we get the integral 3e^-x(1+u^2)du.
Solving this integral, we get the final answer of 3(e^-x-xe^-x+x+1/3e^-x(2+u^3)+C). For question 2, we are asked to solve the integral 4∫(10³dx)/(x²+3x-5)(x+2)²(x-1). This integral requires partial fraction decomposition, where we break the fraction down into simpler fractions with denominators (x+2)², (x+2), and (x-1). After solving for the coefficients, we get the final answer of 4(7/20 ln|x+2| - 9/8 ln|x-1| + 13/40 ln|x+2|^2 - 1/8(x+2)^(-1) + C). In summary, for question 1 we used substitution and for question 2 we used partial fraction decomposition to solve the given integrals.
To learn more about integral, visit:
https://brainly.com/question/32150751
#SPJ11
This is my last question

Answers
Answer:
the first one
Step-by-step explanation:
Answer:
2
Step-by-step explanation:
it is going to be answer 2 because he put more in at the end
What type(s) of symmetry does the figure have? (Check all that apply.)
Line Symmetry
Rotational Symmetry
None
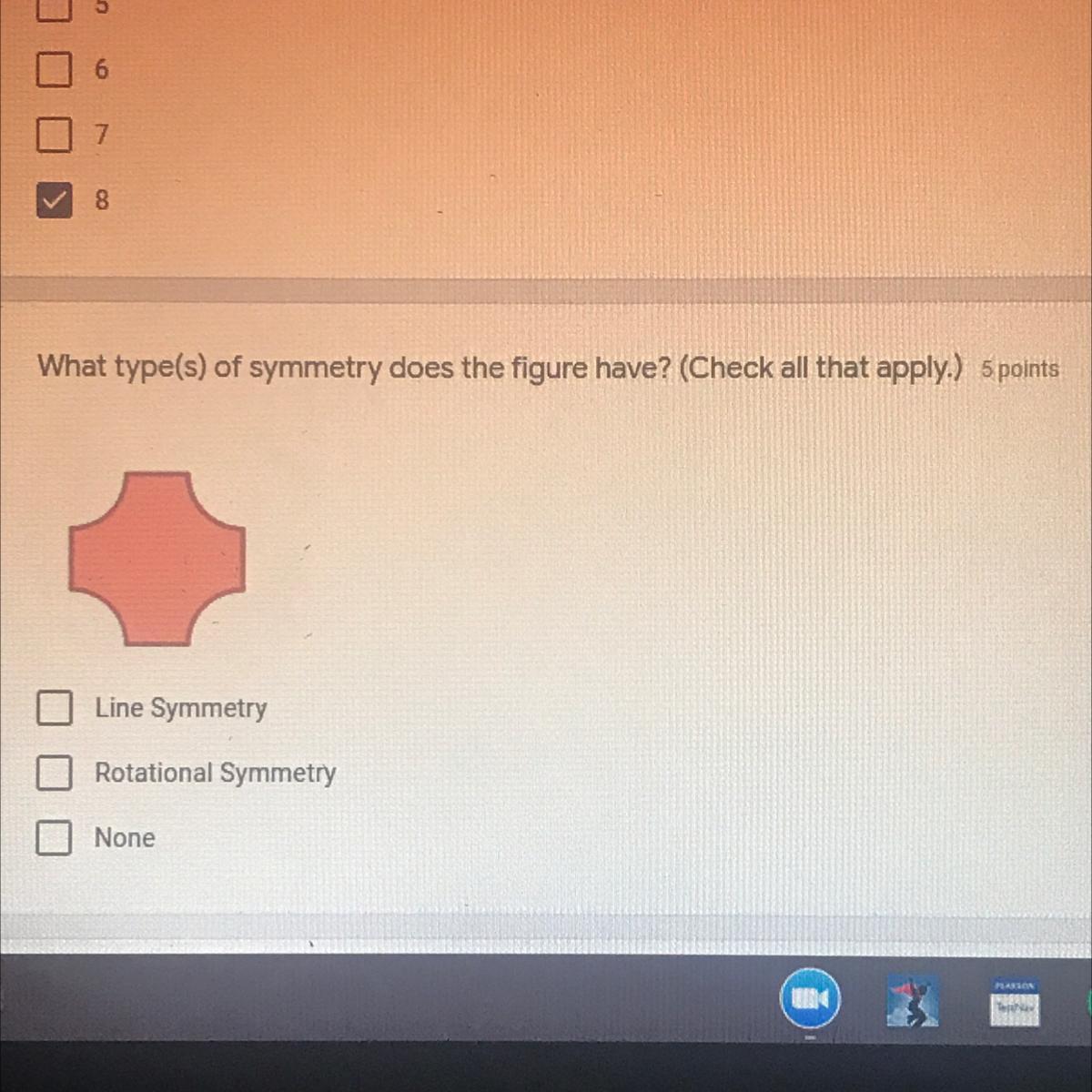
Answers
Answer:
Rotational Symmetry
Step-by-step explanation: It stays the same when rotated
If the ratio of radii of two spheres is 4:7, find the ratio of their volumes.
Answers
Answer:
volume is equal to ratio
Answer:
This is your answer. If I'm right so,
Please mark me as brainliest. thanks!!!

Solve by using a proportion. Round answer to the nearest hundredth of necessary.
A map scale designates 0.75 inch = 50 miles. If the distance between two towns on the map is 2.75 inches, how many miles must you drive
to go from the first town to the second town?
Answer:
miles
Answers
To go from the first town to the second town, you must drive 137.5 miles.
What is an proportion?
A proportion is a mathematical equation that compares two ratios. It is usually written as two equal fractions or ratios, one on each side of the equation. A proportion can be used to compare the relationship between different quantities, such as measurements, rates, or even time.
We can use proportion to solve this problem. The proportion relates the map scale to the actual distance:
0.75 inch / 50 miles = x / distance
where x is the actual distance we want to find.
We can cross-multiply and solve for x:
0.75 inch * distance = 2.75 inches * 50 miles
x = (2.75 inches * 50 miles) / 0.75 inch
x = (137.5 miles)
To go from the first town to the second town, you must drive 137.5 miles.
To learn more about proportion, Visit
https://brainly.com/question/1496357
#SPJ1
the sum of two rational numbers is 2/5. of one of the rational number is -3/7 then find the other rational number
Answers
Answer:
-29/35
Step-by-step explanation:
Using the following information for McDonovan, Inc.'s stock, calculate the standard deviation. State Probability Return Boom 20% 40% Normal 60% 15% Recession 20% -20% 13.19% O 5.27% 17.56%
Answers
The standard deviation of McDonovan, Inc.'s stock returns is approximately 19.54%.
To calculate the standard deviation for McDonovan, Inc.'s stock returns using the provided information, we can use the following steps:
1. Assign weights to each return based on their respective probabilities.
Boom: Probability = 0.20, Return = 0.40
Normal: Probability = 0.60, Return = 0.15
Recession: Probability = 0.20, Return = -0.20
2. Calculate the expected return by taking the weighted average of the returns.
Expected Return = (0.20 × 0.40) + (0.60 × 0.15) + (0.20 × -0.20) = 0.09 or 9%
3. Calculate the squared difference between each return and the expected return.
Boom: (0.40 - 0.09)² = 0.1296
Normal: (0.15 - 0.09)² = 0.0036
Recession: (-0.20 - 0.09)² = 0.0736
4. Calculate the variance by taking the weighted average of the squared differences.
Variance = (0.20 × 0.1296) + (0.60 × 0.0036) + (0.20 × 0.0736) = 0.03808
5. Take the square root of the variance to obtain the standard deviation.
Standard Deviation = √(0.03808) = 0.1954 or 19.54%
Therefore, the standard deviation of McDonovan, Inc.'s stock returns is approximately 19.54%.
Read more on Standard Deviation here: https://brainly.com/question/475676
#SPJ11
ANSWER PLEASE I NEED IT

Answers
Answer:
its the second one
Step-by-step explanation:
evaluate the following:
\(( - 4) ^{3} \)
Answers
Answer:
- 64
Step-by-step explanation:
\((-4)^{3}\)
= - 4 × - 4 × - 4
= 16 × - 4
= - 64
1 in 10,000 white tailed deer on the east coast of the united states carries the lyme disease bacteria. you randomly select a white-tailed deer from a population on the east coast. what is the probability that the deer you select carries the lyme disease bacteria?
Answers
The probability of selecting a white-tailed deer that carries the Lyme disease bacteria is 1 in 10,000, or 0.0001. This means that out of every 10,000 white-tailed deer on the east coast, only one is expected to carry the Lyme disease bacteria.
If we assume that each deer in the population has an equal chance of carrying the bacteria, then the probability of selecting a deer that carries the bacteria can be calculated using the formula for probability:
Probability = Number of desired outcomes / Total number of possible outcomes
In this case, the number of desired outcomes is one (since we want to select a deer that carries the bacteria), and the total number of possible outcomes is the total number of white-tailed deer in the population. Since we don't know the exact number of deer in the population, we can assume that it is very large, so we can use an approximation:
Probability ≈ 1 / (Very large number)
Therefore, the probability of selecting a white-tailed deer from the east coast population that carries the Lyme disease bacteria is very close to 0.0001 or 1 in 10,000.
To know more about probability , refer here :
https://brainly.com/question/30034780#
#SPJ11
30 months =
years
months
Answers
Answer:
2.5 years/2 years 6 months
Step-by-step explanation:
Half year = 6 months
One year = 12 months
Two years = 24 months
30-24=6 months
2 Years + 6 months = 2.5 years/30 months/2 years 6 months
A computer store offers a 5% discount off the list price x for any computer bought with cash, rather than put on credit. At the same time, the manufacturer offers a $ 200 rebate for each purchase of a computer.
c. Suppose the list price of a computer is $ 1500 . Use a composite function to find the price of the computer if the discount is applied before the rebate.
Answers
The price of the computer if the discount is applied before the rebate is $1225. The composite function is (g.f)(x) = g(f(x))
What is the composite function to find the price of the computer if the discount is applied before the rebate?
A computer store offers a 5% discount off the list price x for any computer bought with cashThe list price of a computer is $1500 The manufacturer offers a $200 rebate for each purchase of a computer.
(g.f)(x) = g(f(x))
f(1500) = 0.95(1500)
= 1425
g(1425) = 1425-20
= 1225
= $1225
Therefore, The price of the computer if the discount is applied before the rebate is $1225. The composite function is (g.f)(x) = g(f(x))
To learn more about composite function, refer
https://brainly.com/question/10687170
#SPJ4
Rebecca is playing a video game that involves planting and cutting down trees. She moves up an energy level for each tree she plants, and she moves down a level for each tree she cuts. If Rebecca reaches energy level 10, she will earn bonus points.
Rebecca is currently at energy level 4. The results of her next 3 turns are:
Turn 1: 6 trees cut
Turn 2: 8 trees planted
Turn 3: 1 tree cut
Answer the questions to find out whether Rebecca earned bonus points in the next 3 turns. Use the number line to help you add.
A number line from -5 to 10.
1. Using only addition, write an expression that represents Rebecca's score after these three turns. (Remember that she starts at an energy level of 4.). (2 points)
2. What is Rebecca's energy level after Turn 1? (2 points)
3. What is Rebecca's energy level after Turn 2? (3 points)
4. What is Rebecca's energy level after Turn 3? Will she earn bonus points after Turn 3? Explain why or why not. (3 points)
Answers
In the video game Rebecca is playing using only addition the expression that represents Rebecca's score after these three turns is
= 4 + (-6) + (8) + (-1)
Rebecca's energy level after Turn 1 = -2
Rebecca's energy level after Turn 2 = 6
Rebecca's energy level after Turn 3 = 7
she will not earn bonusHow to find the expression that represents Rebecca's scoreFollowing the rule of the video game the expression is written in steps below
Rebecca is currently at energy level 4
= 4
Turn 1: 6 trees cut
= 4 + (-6)
= 4 - 6
= -2
Turn 2: 8 trees planted
= 4 + (-6) + (8)
= -2 + 8
= 6
Turn 3: 1 tree cut
= 4 + (-6) + (8) + (-1)
= 6 - 1
= 7
Learn more about addition at:
https://brainly.com/question/25421984
#SPJ1
For compound interest loans and investments, the annual percentage rate (APR) is the annual interest rate without taking compound interest into account. The annual percentage yield (APY) is the effective annual rate and includes the effects of compounding within the year. Consider a loan of $1000 with a 15% APR compounded monthly. Round your answers to the nearest cent
Answers
The total amount of interest paid along with annual rate is $163.80 at 16.08%.
The annual percentage rate refers to the yearly rated interest which is taken from when the individual takes a loan. It is also considered a measure of the cost of credit or borrowing expense which involves a interest and fees concerning the transaction.
And an annual percentage yield is helpful in the effective annual rate which includes the points of compounding given in that year.
For the given loan of $1000 with a 15% APR compounded monthly,
The evaluated monthly interest rate would be
15%/12 = 1.25%.
The total evaluated amount of interest paid on the course of a year will be $163.80.
The current effective annual rate will be 16.08%.
The total amount of interest paid along with annual rate is $163.80 at 16.08%.
To learn more about annual percentage rate ,
https://brainly.com/question/24715857
#SPJ4
madelyn is creating a media center. there are 7 televisions and 7 sets of speakers to choose from. for the dvd player, madelyn has 2 options. how many different entertainment centers can madelyn make?
Answers
The total number of different entertainment centers Madelyn can make is 7 × 7 × 2 = 98. Answer: 98.
Madelyn is creating a media center.
There are 7 televisions and 7 sets of speakers to choose from. For the DVD player, Madelyn has 2 options.
We are supposed to determine how many different entertainment centers Madelyn can make.
Therefore, we need to use the multiplication principle of counting.
According to the multiplication principle of counting, if an event can occur in m ways and a second event can occur in n ways, then the two events can occur in m x n ways.
Let's use the multiplication principle of counting to solve this problem.
The number of ways Madelyn can choose a TV is 7.
The number of ways Madelyn can choose a set of speakers is 7.
The number of ways Madelyn can choose a DVD player is 2.
Therefore, the total number of different entertainment centers Madelyn can make is 7 × 7 × 2 = 98. Answer: 98.
Know more about number here:
https://brainly.com/question/25734188
#SPJ11
It costs $60 per hour to rent a jet ski. The total cost of a jet ski rental
includes a flat fee of $20 plus the hourly fee. Which equation represents
the situation?
Answers
Answer:
y = 60x + 20
Step-by-step explanation:
The number of hours that we ski is a variable cost where each hour costs $60. On top of that, we have a fixed cost of $20 which stays the same no matter how long we ski.
So we can use an equation to find the totla cost C given the number of hours t as follows:
C(t) = 60t + 20
We can use this equation to find the cost of a skiing session by plugging in some value for t. For example, if we ski for 3 hours:
C(3) = 60(3) + 20 = $200
The equation can also be written using x and y and mean the same thing.
1.2.1 The number of pieces of ropes for FIVE cuts. 1.2.2 The general formula (Ta), for the number of rope pieces. 1.2.3 How many rupe cuttings will make up 153 rope pieces? 1.2.4 How many ropes pieces will result from 11 cuttings? 5 Please tu

Answers
Step 1
The number of pieces for 5 cuts is
\(7+4=11\)Step 2
The general formula Tn, for the number of rope pieces is
\(\begin{gathered} a=3 \\ d=2 \\ T_n=3+(n-1)2 \\ T_n=2n+1 \end{gathered}\)Step 3
How many rope cuttings will make up 153 rope pieces
\(\begin{gathered} 153=2n+1 \\ 152=2n \\ \frac{152}{2}=\frac{2n}{2} \\ n=76\text{ rope cuttings} \end{gathered}\)Step 4
How many ropes pieces will result from 11 cuttings
\(\begin{gathered} T_n=2(11)+1 \\ T_n=23\text{ rope pieces} \end{gathered}\)find the missing side

Answers
Answer:
7) 8.94
8) 6.71
Step-by-step explanation:
for both questions, use pythagorean theorem
\(a^{2} + b^{2} = c^{2}\)
Question 7:
\(4^{2} + 8^{2} = c^{2}\)
16 + 64 = \(c^{2}\)
80 = \(c^{2}\)
\(\sqrt{80} = \sqrt{c^{2}}\)
c = 8.94
Question 8:
\(6^{2} + 3^{2} = c^{2}\)
36 + 9 = \(c^{2}\)
45 = \(c^{2}\)
\(\sqrt{45} = \sqrt{c^{2} }\)
c = 6.71
find the best estimate for the unicity distance for affine cipher. group of answer choices 1.33 2.35 3.33 2.66 1.75
Answers
The closest answer choice to this value is option 1, 33. Therefore, the best estimate for the unicity distance for an affine cipher is 33.
To find the best estimate for the unicity distance for an affine cipher, we can use the following formula:
Unicity Distance (U) = (keyspace / entropy) × log2(1 / redundancy).
Given the answer choices:
1. 33
2. 35
3. 33
4. 26
5. 17.5
For an affine cipher, the keyspace is 26^2 (since there are 26 possibilities for both 'a' and 'b' in the equation
y = (ax + b) mod 26).
The entropy of English text is roughly 1.5 bits/character, and the redundancy is approximately 0.7.
Using the formula, we have:
U = (26^2 / 1.5) × log2(1 / 0.7)
U ≈ 33.49
Therefore, the best estimate for the unicity distance for an affine cipher is 33.
for such more question on unicity distance
https://brainly.com/question/31483371
#SPJ11
HELP! Georgie took 275 mg of medicine for her cold in the first hour she got home from work. In each subsequent hour, the amount of
medicine in her body is 91% of the amount from the previous hour.
What is the explicit rule for the amount of medicine remaining in her body in the nth hour and approximately how much medicine
would remain in the 8th hour?
Round to two decimal places.
Drag and drop the answers into the boxes to match the situation.
Explicit rule
Amount of medicine, in mg, during the 8th hour.

Answers
Answer:
here is the ananswer
Step-by-step explanation:
red go to red and black to black

3. Find \( y^{\prime} \) for the following implicit function \( y^{2}-x^{2} y=-2 \)
Answers
The derivative \(\( y' \)\) of the implicit function \(\( y^2 - xy = -2 \)\) is 0, indicating a constant slope with no change in relation to \(\( x \)\).
To find \(\( y' \)\)for the implicit function \(\( y^2 - xy = -2 \)\), we can differentiate both sides of the equation with respect to \(\( x \)\) using the chain rule. Let's go step by step:
Differentiating \(\( y^2 \)\) with respect to \(\( x \)\) using the chain rule:
\(\[\frac{d}{dx}(y^2) = 2y \cdot \frac{dy}{dx}\]\)
Differentiating \(\( xy \)\) with respect to \(\( x \)\) using the product rule:
\(\[\frac{d}{dx}(xy) = x \cdot \frac{dy}{dx} + y \cdot \frac{dx}{dx} = x \cdot \frac{dy}{dx} + y\]\)
Differentiating the constant term (-2) with respect to \(\( x \)\) gives us zero since it's a constant.
So, the differentiation of the entire equation is:
\(\[2y \cdot \frac{dy}{dx} - (x \cdot \frac{dy}{dx} + y) = 0\]\)
Now, let's rearrange the terms:
\(\[(2y - y) \cdot \frac{dy}{dx} - x \cdot \frac{dy}{dx} = 0\]\)
Simplifying further:
\(\[y \cdot \frac{dy}{dx}\) \(- x \cdot \frac{dy}{dx} = 0\]\)
Factoring out:
\(\[(\frac{dy}{dx})(y - x) = 0 \]\)
Finally, solving:
\(\[\frac{dy}{dx} = \frac{0}{y - x} = 0\]\)
Therefore, the derivative \(\( y' \)\) of the given implicit function is 0.
Learn more about derivative
brainly.com/question/29144258
#SPJ11