.4 ÷ 28.08 Dividing Decimals , Divide to the nearest Tenth??
I Will Give You 10 Points
Answers
Answer:
0
Step-by-step explanation:
The answer is 0.01424, but if you round it to the nearest tenth, you would end up with 0.
Related Questions
The integer -2-(-5) can also be written as
Answers
Answer: Hello!
-2-(-5) can also be written as -2 + 5.
When subtracting a negative, you're essentially adding, because you are subtracting a negative value. So we would add 5 to -2.
Hope this helps!
What is the value of this expression
-16+12
A.-28
B.-4
C.4
D.28
Answers
If y=5 Evaluate the expression 3y by substituting the value for the variable
Answers
Answer: 15
Step-by-step explanation:
y = 5
3(y) = answer
3(5) = 15.
What is the key difference betweenstudent submitted image, transcription available belowandstudent submitted image, transcription available belowWhat assumption(s) do you need to show thatstudent submitted image, transcription available belowis unbiased? What does this mean, practically?
Answers
The key difference between two student submissions is not specified in the question. To demonstrate that a student-submitted image or transcription is unbiased, certain assumptions need to be met. Understanding the practical implications of unbiasedness is crucial.
The question does not provide information about the specific differences between the student-submitted image and transcription. However, to establish that a student submission is unbiased, several assumptions need to be satisfied. These assumptions typically include random sampling, the absence of systematic errors or biases in the data collection process, and the independence of observations. If these assumptions are met, it suggests that the student submission accurately represents the underlying population or phenomenon being studied.
Practically, unbiasedness means that the student-submitted image or transcription provides an accurate and representative depiction of the information or data being examined. It indicates that the student's work is not influenced by any systematic errors or biases that could skew the results or distort the information. This is important in research or data analysis to ensure the validity and reliability of the findings and conclusions drawn from the student's submission.
Learn more about errors here:
https://brainly.com/question/30759250
#SPJ11
Https://imgur.com/a/n3PRcMY
Answers
20 = 2x.
That means x = 10
2. Easy now that u have x. Angle 1 is 3x + 10, which means its 3(10) + 10 which is 40
how many cubes, with side measures of 2 cm, will fit inside a right rectangular prism with dimensions of 6 cm by 8 cm by 4 1 2 cm? group of answer choices 24 108 54 27
Answers
Answer:
Using the volume formula we know that (B) 27 cubes can be fitted into the right rectangular prism.
What is the right rectangular prism?
The right rectangular prism has four rectangle-shaped side faces and two parallel end faces that are perpendicular to each of the bases.
Parallelograms make up the sides of an oblique prism, a non-right rectangular prism.
A cuboid is yet another name for a right rectangle prism.
So, the volume of the right rectangular prism:
V = wlh
Insert values:
V = wlh
V = 6*8*4.5
V = 216cm³
Now, the volume of the cube:
V = a³
V = 2³
V = 8cm³
Then, the number of cubes that can be fitted in the right rectangular prism:
216/8 = 27
Therefore, using the volume formula we know that (B) 27 cubes can be fitted into the right rectangular prism.
Know more about the right rectangular prism? here:
brainly.com/question/3317747
#SPJ1
Correct question:
How many cubes, with side measures of 2 cm, will fit inside a right rectangular prism with dimensions of 6 cm by 8 cm by 4 1/2 cm?
Group of answer choices
a. 24
b. 27
c. 108
d. 54
The final answer is 27
To determine how many cubes will fit inside the right rectangular prism, we need to find the volume of the prism and the volume of the cubes, then divide the volume of the prism by the volume of the cubes.
Volume of a cube (V_cube) = side^3
V_cube = 2 cm * 2 cm * 2 cm = 8 cubic cm
Volume of the right rectangular prism (V_prism) = length * width * height
V_prism = 6 cm * 8 cm * 4.5 cm = 216 cubic cm
Now, divide the volume of the prism by the volume of the cubes:
Number of cubes = V_prism / V_cube = 216 cubic cm / 8 cubic cm = 27 cubes
Therefore, 27 cubes with side measures of 2 cm will fit inside the right rectangular prism.
To know more about cubes visit : https://brainly.com/question/28134860
#SPJ11
32.8g of sugar is needed to make 4 cakes. How much sugar is needed for 7 cakes?
Answers
Answer:
57.4g
Step-by-step explanation:
32.8g of sugar is needed to make 4 cakes. How much sugar is needed for 7 cakes?
From the above questions, we know that:
4 cakes = 32.8g
7 cakes = x g
Cross Multiply
4 × xg = 7 × 32.8g
x = 7 × 32.8g/4
x = 57.4 g
Therefore, 57.4g is needed for 7 cakes
The unit fraction 1/5 represents the space between the tick marks on the number line. write the addition expression being modeled. then find the sum.
Answers
The addition expression being modeled by the unit fraction 1/5 representing the space between the tick marks on the number line is 1/5 + 1/5 + 1/5 + 1/5 + 1/5. The sum is 1.
When we add the fractions, we combine the numerators while keeping the same denominator:
1/5 + 1/5 + 1/5 + 1/5 + 1/5 = (1 + 1 + 1 + 1 + 1) / 5
Simplifying the numerator, we get:
5/5 = 1
Therefore, the sum of the unit fraction 1/5 repeated five times is equal to 1. This means that when we add the space between five tick marks on the number line, we cover the distance of one whole unit.
Learn more about fraction here:
https://brainly.com/question/30154928
#SPJ11
What is the most widely used probability model for continuous numerical variables?.
Answers
Answer:
The most widely used continuous probability distribution in statistics is the normal probability distribution.
Step-by-step explanation:
The graph corresponding to a normal probability density function with a mean of μ = 50 and a standard deviation of σ = 5 is shown in Figure 3. Like all normal distribution graphs, it is a bell-shaped curve.
the area of a triangle 17.5 square meters. The height of the triangle is 3 meters less than twice it’s base. the base of the triangle is x meters
Answers
Answer :
Given that the base of the triangle is x m, the height is 3m less than twice it's base then the height will be represented by the equation:
(2x-3) m
Thus the area will be:
Area=1/2bh
Area=1/2x(2x-3)=17.5
x^2-1.5x=17.5
Writing the above equation is quadratic form of ax^2+bx+c=0 we get:
x^2-1.5x-17.5=0
how to do constrained maximization when the constraint means the maximum point does not have a derivative of 0
Answers
To do constrained maximization when the constraint means the maximum point does not have a derivative of 0, you can use the following steps:
Write down the objective function and the constraint.Solve the constraint for one of the variables.Substitute the solution from step 2 into the objective function.Find the critical points of the objective function.Test each critical point to see if it satisfies the constraint.The critical point that satisfies the constraint is the maximum point.How to explain the informationWhen dealing with constrained maximization problems where the constraint does not involve a derivative of zero at the maximum point, you need to utilize methods beyond standard calculus. One approach commonly used in such cases is the method of Lagrange multipliers.
The Lagrange multiplier method allows you to incorporate the constraint into the optimization problem by introducing additional variables called Lagrange multipliers.
Learn more about maximization on
https://brainly.com/question/13464288
#SPJ1
The height of a doorway is 7 yards. What is the height of the doorway in inches?
The height of the doorway is ____ inches.
Answers
Resolve the expression \(\frac{(x-2)}{(x^{2} +1)(x-1)^{2} }\) into the simplest partial fractions
Answers
The partial fraction expansion will look like
(x - 2)/((x ² + 1) (x - 1)²) = (ax + b)/(x ² + 1) + c/(x - 1) + d/(x - 1)²
Get everything in terms of a common denominator, and compare the numerators on both sides:
x - 2 = (ax + b) (x - 1)² + c (x ² + 1) (x - 1) + d (x ² + 1)
Expand the right side:
x - 2 = (ax + b) (x - 1)² + c (x ² + 1) (x - 1) + d (x ² + 1)
x - 2 = (a + c) x ³ + (-2a + b - c + d) x ² + (a - 2b + c) x + b - c + d
Match up the coefficients and solve the resulting system of equations:
a + c = 0
-2a + b - c + d = 0
a - 2b + c = 1
b - c + d = -2
==> a = -1, b = -1/2, c = 1, d = -1/2
So the expansion into partial fractions is
(x - 2)/((x ² + 1) (x - 1)²) = (-x - 1/2)/(x ² + 1) + 1/(x - 1) - 1/(2 (x - 1)²)
… = -(2x + 1)/(2 (x ² + 1)) + 1/(x - 1) - 1/(2 (x - 1)²)
There is a bag with only red marbles and blue marbles. The probability of randomly choosing a red marble is 1 /9 . There are 63 marbles in total in the bag and each is equally likely to be chosen. Work out how many red marbles there must be.
Answers
Answer: 7 red marbles.
Step-by-step explanation:
Since we are given the information that there are only red marbles and blue marbles in the bag and that the probability of randomly choosing a red marble is 1 /9 while there are 63 marbles in total.
Then the number of red marbles will be:
= 1/9 × 63
= 7
There are 7 red marbles
The number if blue marbles will be:
= 63 - 7
= 56 blue marbles
Level 2.0
1) Circle any like terms in the expression:
2x - 8y + 3x - 2h + 9x + 3p
Answers
The like terms in the expression are, 2x, 3x, and 9x.
What is like terms?
Like words in algebra are those that share the same variables and powers. It is not required that the coefficients line up. Contrary terms are two or more terms that do not share the same variables or powers, making them different terms. Unless there is a power, the order of the variables is irrelevant.
Consider, the given expression
2x - 8y + 3x - 2h + 9x + 3p
In this expression there are four variables, x, y, h and p.
The x variable having three terms with same power.
Since, if the variables having same power, then the terms are like terms.
Here, 2x, 3x and 9x having same power 1.
So, these terms are like terms.
Hence, the like terms in the expression are, 2x, 3x and 9x.
To know more about the like terms, click on the link
https://brainly.com/question/15894738
#SPJ1
Solve for e
re + p = 4t
Answers
Answer:
e = (4t - p)/r
Step-by-step explanation:
If you are solving for e, you want to get e alone.
Rewrite the equation
re + p = 4t
Subtract p from both sides
re = 4t - p
Divide both sides by r
e = 4t - p /r or e = (4t - p)/r
dif .Use the Ksp values in table 18.2 or Appendix II in your textbook to calculate the molar solubility of each compound in pure water (mandatory write the chemical equation describing heterogeneous equilibrium in saturated solution and corresponding expression for K sp ) : (A)CuS (B) Ag2CrO4(C) Ca(OH)2 (D) Ca3(PO4) 2
Answers
The molar solubility of CuS is 2.45 × 10-19 M, the molar solubility of Ag2CrO4 is 2.4 × 10-5 M, the molar solubility of Ca(OH)2 is 3.05 × 10-3 M, and the molar solubility of Ca3(PO4)2 is 7.4 × 10-6 M.
Solubility of a compound is defined as the maximum amount of solute that can be dissolved in a given amount of solvent at a specific temperature. When a solution is saturated, it means that no more solute can be dissolved at that temperature. The solubility product constant (Ksp) is the equilibrium constant for a solid substance dissolving in an aqueous solution. It is defined as the product of the concentrations of the ions raised to the power of their stoichiometric coefficients.
The chemical equation describing the heterogeneous equilibrium in a saturated solution and the corresponding expression for Ksp for each compound is as follows:
(A) CuS: CuS(s) ↔ Cu2+(aq) + S2-(aq)Ksp
= [Cu2+][S2-](B) Ag2CrO4: Ag2CrO4(s)
↔ 2Ag+(aq) + CrO42-(aq)Ksp
= [Ag+]2[CrO42-](C) Ca(OH)2: Ca(OH)2(s)
↔ Ca2+(aq) + 2OH-(aq)Ksp
= [Ca2+][OH-]2(D) Ca3(PO4)2: Ca3(PO4)2(s)
↔ 3Ca2+(aq) + 2PO43-(aq)Ksp
= [Ca2+]3[PO43-]2
Using the Ksp values from Appendix II in the textbook, the molar solubility of each compound in pure water is as follows:
(A) CuS:Ksp = 6.0 × 10-37= [Cu2+][S2-]
If x is the molar solubility of CuS, then
[Cu2+] = x and [S2-] = x.
Substituting these values in the expression for Ksp, we get:x2 = 6.0 × 10-37x = 2.45 × 10-19 M(B) Ag2CrO4:Ksp = 1.1 × 10-12= [Ag+]2[CrO42-]If x is the molar solubility of Ag2CrO4, then [Ag+] = 2x and [CrO42-] = x.
Substituting these values in the expression for Ksp, we get:
4x3 = 1.1 × 10-12x
= 2.4 × 10-5 M
(C) Ca(OH)2:Ksp = 4.68 × 10-6= [Ca2+][OH-]2
If x is the molar solubility of Ca(OH)2, then [Ca2+] = x and [OH-] = 2x.
Substituting these values in the expression for Ksp, we get:
4x3 = 4.68 × 10-6x = 3.05 × 10-3 M
(D) Ca3(PO4)2:Ksp = 2.0 × 10-29= [Ca2+]3[PO43-]2If x is the molar solubility of Ca3(PO4)2, then
[Ca2+] = 3x and [PO43-] = 2x.
Substituting these values in the expression for Ksp, we get:
108x5
= 2.0 × 10-29x
= 7.4 × 10-6 M.
To know more about molar solubility visit:-
https://brainly.com/question/31043999
#SPJ11
Answer:
The Ksp value for Ca3(PO4)2 can be found in Table 18.2 or Appendix II in the textbook.
Step-by-step explanation:
To calculate the molar solubility of each compound in pure water, we need to utilize the solubility product constant (Ksp) values and write the corresponding chemical equations for their heterogeneous equilibrium. Let's calculate the molar solubility for each compound:
(A) CuS:
The chemical equation for the heterogeneous equilibrium in saturated solution is:
CuS(s) ⇌ Cu2+(aq) + S2-(aq)
The expression for the solubility product constant (Ksp) is:
Ksp = [Cu2+][S2-]
The Ksp value for CuS is not provided in the question. To calculate the molar solubility, we need the corresponding Ksp value.
(B) Ag2CrO4:
The chemical equation for the heterogeneous equilibrium in saturated solution is:
Ag2CrO4(s) ⇌ 2Ag+(aq) + CrO42-(aq)
The expression for the solubility product constant (Ksp) is:
Ksp = [Ag+]^2[CrO42-]
The Ksp value for Ag2CrO4 can be found in Table 18.2 or Appendix II in the textbook.
(C) Ca(OH)2:
The chemical equation for the heterogeneous equilibrium in saturated solution is:
Ca(OH)2(s) ⇌ Ca2+(aq) + 2OH-(aq)
The expression for the solubility product constant (Ksp) is:
Ksp = [Ca2+][OH-]^2
The Ksp value for Ca(OH)2 can be found in Table 18.2 or Appendix II in the textbook.
(D) Ca3(PO4)2:
The chemical equation for the heterogeneous equilibrium in saturated solution is:
Ca3(PO4)2(s) ⇌ 3Ca2+(aq) + 2PO43-(aq)
The expression for the solubility product constant (Ksp) is:
Ksp = [Ca2+]^3[PO43-]^2
Please refer to the provided textbook for the specific Ksp values of Ag2CrO4, Ca(OH)2, and Ca3(PO4)2 in order to calculate their molar solubilities.
To know more about saturated solution
https://brainly.in/question/29235078
#SPJ11
A rocket is sent into space. When the power dies out, the rocket will just keep floating and moving in space forever (unless an unbalanced force, such as a meteor, runs into it
Answers
A rocket sent into space will continue to move in space indefinitely unless acted upon by an external force.
In the absence of external forces, such as gravity or atmospheric drag, an object in motion will remain in motion with a constant velocity according to Newton's first law of motion, also known as the law of inertia. This means that once the rocket's engines have powered it into space and the power source is depleted, there are no forces to slow it down or bring it to a stop. Therefore, the rocket will continue to float and move in space with its current velocity.
However, it is important to note that space is not entirely empty, and there are various objects present, such as asteroids, comets, and other celestial bodies. If the rocket were to collide with any of these objects, it would experience an unbalanced force that could alter its trajectory or cause it to stop moving. But in the absence of such collisions, the rocket will continue its motion in space indefinitely.
It is worth mentioning that even in the absence of external forces, factors like gravity from nearby celestial bodies can have a subtle influence on the rocket's trajectory over time. Nonetheless, the rocket will essentially continue its motion unless acted upon by an unbalanced force, as described in Newton's first law of motion.
Learn more about external force here
https://brainly.com/question/30369473
#SPJ11
How doe the location of the negative make value of 5. 3 x 10^-4 different from -5. 3 x 10^4
Answers
Location of the negative make value different from each other that is 5.3/10^4 and -(5.3 * \(10^{4}\))
According to this rule, if the exponent is negative, we can change the exponent into positive by writing the same value in the denominator and the numerator holds the value 1.
The negative exponent rule is given as:
5. 3 x 10^-4
= 5.3/10^4 (1)
-5. 3 x 10^4
-(5.3 * \(10^{4}\)) (2)
from equation 1 and 2 these two equations are different from each other.
location of the negative make value different from each other that is 5.3/10^4 and -(5.3 * \(10^{4}\))
To know more about Exponent Rule visit brainly.com/question/29125740
#SPJ4
5.Twenty-four dogs are in a kennel. Twelve of the dogs are black, six of the dogs have
short tails, and fifteen of the dogs have long hair. There is only one dog that is black with
a short tail and long hair. Two of the dogs are black with short tails and do not have long
hair. Two of the dogs have short tails and long hair but are not black. 6 dogs are only
black. How many dogs are black with long hair but do not have short tails. How many
have only Long hair?
Answers
Answer:
Step-by-step explanation: yes
Please help first real answer will get brainliest

Answers
Answer:
6
Step-by-step explanation:
a1(n-1) + D
d = 6
Give an example of a group in which all non-identity elements having infinite order. Also give an example of a group in which for every positive integer n, there exist an element of order n.
Answers
Example 1:
An example of a group in which all non-identity elements have infinite order is the additive group of integers, denoted as (Z, +). In this group, the operation is ordinary addition. Every non-zero integer can be written as the sum of 1 repeated infinitely many times or -1 repeated infinitely many times, resulting in infinite orders for all non-identity elements. For instance, consider the element 1 in this group. If we add 1 to itself repeatedly, we obtain the sequence 1, 2, 3, 4, and so on, which extends infinitely. Similarly, adding -1 to itself repeatedly generates the sequence -1, -2, -3, -4, and so forth. Thus, every non-zero element in the additive group of integers has an infinite order.
Example 2:
An example of a group in which for every positive integer n, there exists an element of order n is the multiplicative group of positive rational numbers, denoted as (Q+, ×). In this group, the operation is ordinary multiplication. For any positive integer n, we can find an element whose exponentiation by n gives the identity element 1. Specifically, let's consider the element 2^(1/n). If we multiply this element by itself n times, we get (2^(1/n))^n = 2^(n/n) = 2^1 = 2, which is the identity element in the group. Therefore, the element 2^(1/n) has an order of n. This applies to every positive integer n, meaning that for any n, we can find an element in the multiplicative group of positive rational numbers with an order of n.
In summary, the additive group of integers (Z, +) exemplifies a group where all non-identity elements have infinite order, while the multiplicative group of positive rational numbers (Q+, ×) demonstrates a group where for every positive integer n, there exists an element with an order of n.
Learn more about Infinite :
https://brainly.com/question/30238078
#SPJ11
i need help please and thanks

Answers
4. Mark's age, when doubled, is Peggy's age. Peggy is 6 years older than Chris. Chris is 6 years older than
Mark. How much older is Peggy than Mark?
Answers
In ABC, a = 4, b = 3, and c = 3. What is the
value of cos A?

Answers
The value of cos A in the triangle is 1 / 9.
How to find the angle of a triangle?The triangle is given as ABC. The side lengths are a, b and c. Therefore, cos A of the triangle can be found using cosine rule as follows:
a² = b² + c² - 2bc cos A
a = 4
b = 3
c = 3
Therefore,
4² = 3² + 3² - 2(3)(3) cos A
16 = 9 + 9 - 18 cos A
16 - 18 = - 18 cos A
-2 = - 18 cos A
divide both sides by - 18
cos A = - 2 / - 18
cos A = 1 / 9
learn more on triangle here:https://brainly.com/question/16800749
#SPJ1
An equiangular triangle has one side of length six inches. What is the height of the triangle, drawn from that side, to the nearest tenth of an inch?
height = ------------- in.

Answers
Answer:
5.2
Step-by-step explanation:
Construct an altitude. Using the Pythagorean theorem, the height is \(\sqrt{6^2-3^2} \approx 5.2\)
g The sides of a rhombus are 12 units long, and one of its angles has a measure of 60 degrees. How long is the other diagonal
Answers
The length of the other diagonal of the rhombus is 24 units.
A rhombus is a parallelogram with four equal sides. Since the sides of the rhombus are 12 units long, all the sides are equal in length. One of the angles of the rhombus measures 60 degrees.
In a rhombus, the diagonals bisect each other at right angles, dividing the rhombus into four congruent right-angled triangles. The angle between the two diagonals is 60 degrees, which means that each right-angled triangle in the rhombus has a 30-degree angle.
To find the length of the other diagonal, we can use trigonometry. In a right-angled triangle with a 30-degree angle, the ratio of the length of the side opposite the angle to the length of the hypotenuse is 1/2. In this case, the side opposite the 30-degree angle is half the length of the diagonal we are trying to find.
Let's denote the length of the other diagonal as "d". Using trigonometry, we can set up the following equation:
sin(30 degrees) = (d/2) / 12
Simplifying the equation, we have:
1/2 = (d/2) / 12
Cross-multiplying, we get:
d/2 = 12 * 1/2
d/2 = 6
Multiplying both sides by 2, we find:
d = 12
Therefore, the length of the other diagonal of the rhombus is 24 units.
Learn more about rhombus
brainly.com/question/12665650
#SPJ11
984759.995148 to the nearest whole number.
Answers
Answer:
984760
Step-by-step explanation:
Point A has coordinates (3, 4). After a translation 4 units left, a reflection across the -axis, and a translation 2 units down, what are the coordinates of the image?
Answers
Answer: (-1,-6)
Step-by-step explanation:
First, you move 4 spaces left getting you to (-1,4). Then you reflect across the X-axis (a reflection means to mirror over a point of symmetry, which in this case is the X-axis) which gets you to (-1,-4). Finally, you move 2 units down getting you to your answer of (-1,-6)
solve this plz plz plz plz plz plz plz!
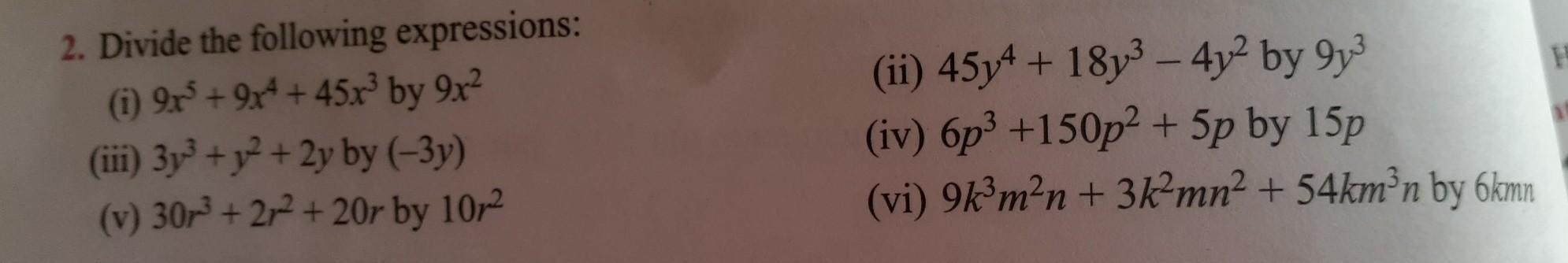
Answers
Answer is attached with image.

