(-3x^3+5x^2-6x-7) / (x+4)
Answers
The solution to the division of the polynomial equation is \(=-3x^2+17x -74 +\dfrac{289}{x+4}\)
The division of the polynomial equation:Polynomial long division is an extended form of the well-known arithmetic method of long division used in algebra to divide one polynomial with another polynomial of the same or lower degree. Addressing a difficult division issue and breaking it into manageable pieces makes it feasible to solve by using this method.
From the given information, we Divide:
\(=\dfrac{(-3x^3+5x^2-6x-7)}{(x+4)}\)
\(=-3x^2+\dfrac{17x^2-6x-7}{x+4}\)
Divide: \(\dfrac{17x^2-6x-7}{x+4}\)
\(=-3x^2+17x + \dfrac{-74x-7}{x+4}\)
Divide: \(=\dfrac{-74x-7}{x+4}\)
\(=-3x^2+17x -74 +\dfrac{289}{x+4}\)
Learn more about the division of quadratic polynomial equations here:
https://brainly.com/question/1214333
#SPJ1
Related Questions
please help me i can really use it

Answers
Note that the complete proof is given as follows:
AB/EB = CB/DB - Given
∠ABC ≅ EBD - Opposite Angles
Thus, ΔABC~ΔEBD - SAS Postulate.
What is the SAS Postulate?
If two sides and an included angle in one triangle are congruent with two sides and an included angle in another, the two triangles are congruent. This is the Side - Angle - Side Postulate.
Angle-Side-Angle (ASA) Congruence Postulate, on the other hand, states that if two angles and the added side in one triangle are congruent to two angles and the included side in another triangle, then the two triangles are congruent.
In the above proof, we demonstrated that Side AB ~ BE and that Sides CB is similar to DB on the bases on the similarity of ratios.
Learn more about SAS Postulate:
https://brainly.com/question/1593616
#SPJ1
help me please brainlist if right

Answers
Step-by-step explanation:
1B.) Zero power rule
C.) 1
2B.) Product of powers rule
C.) y^(7+11) = y^18
3B.) Quotient of powers rule
C.) b^(18-5) =b^13
4B.) Power of a power rule
C.) 3^(2×2) =3^4= 81
5B.) None
C.) 729
Find the x value?
Help pls

Answers
Answer:
Step-by-step explanation:
sin(63°) = x/22
x = 22sin(63°) ≅ 19.6 units
a group of 202 202202 people went on an overnight camping trip, taking 60 6060 tents with them. some of the tents held 2 22 people each, and the rest held 4 44 people each. assuming all the tents were filled to capacity and every person got to sleep in a tent, exactly how many of the tents were 2 22-person tents?
Answers
The answer to the question is that there were 101.1010 2-person tents.
The formula to solve this problem is: (202 ÷ 2) + (202 ÷ 4) = number of tents.
To calculate the number of 2-person tents, we need to divide the number of people (202) by 2, and then add the result to the number of tents we get when we divide the number of people by 4.
So, (202 ÷ 2) + (202 ÷ 4) = 60.6060 tents.
To find out how many of these tents are 2-person tents, we need to divide the number of people (202) by 2. This gives us the result of 101.1010. This is the number of 2-person tents.
So, to summarise, the answer to the question is that there were 101.1010 2-person tents.
The answer to the question is that there were 101.1010 2-person tents.
Learn more about number of people here:
https://brainly.com/question/15839036
#SPJ4
Please help me, I am lost from 3.2 going down

Answers
a store prints a request on each receipt asking customers to fill out a satisfaction survey online if they are willing. what type of sample is this?
Answers
The type of sample that a store prints a request on each receipt asking customers to fill out a satisfaction survey online if they are willing is a voluntary response sample.
In the statistics world, a voluntary response sample is a research sample that relies on individual self-selection. This is in opposition to random sampling, in which the samples are gathered in a way that ensures everyone in a particular population has an equal chance of being chosen. This method of self-selection is also known as self-selection bias or sampling bias.Voluntary response samples are subject to a variety of flaws. The responses may not be representative of the population as a whole, and they may be skewed by numerous factors, such as which individuals are most likely to volunteer, how these volunteers differ from the population as a whole, and how the survey questions are phrased.The results of a voluntary response survey may be useful in generating hypotheses or gaining a general sense of how individuals feel about a particular subject. However, they are not reliable enough to draw any conclusions or to be taken seriously in the scientific sense.
To know more about sample refer here:
https://brainly.com/question/13287171
#SPJ11
Use the drop-down menu complete the statement. The quotient of 3 divided by 3/4 is?
Answers
Answer:
1/4
Step-by-step explanation:
easyyy
I need it FAST please

Answers
Answer:
−30.500
Step-by-step explanation:
Solve : 2y+61 = 0
Subtract 61 from both sides of the equation : 2y = -61
Divide both sides of the equation by 2:y = -61/2 = -30.500
Answer:
-30.5
Step-by-step explanation:
-4(8+y)=90
-32-4y=90
-4y=122
y=-30.5
What are the 5 congruence theorems?.
Answers
The five rules of congruence theorem are described below.
Statement of congruence.The sign for congruence is ≅ and we compose △ABC≅△DEF. ∠A relates to ∠D, ∠B compares to ∠E, and ∠C relates to ∠F. Side Stomach muscle relates to DE,BC compares to EF, and AC relates to DF.
Five rules of congruence theorem:Side-Side-Side(SSS):Corresponding sides of two triangles are equal, then triangles are congruent.
Side-Angle-Sid(SAS):Corresponding two sides and one angle are equal, then triangles are congruent.
Angle-Side- Angle(ASA):One side and two angles are equal, then triangles are congruent.
Angle-Angle-Side(AAS):Corresponding conductive two angles and one side are equal, then triangles are congruent.
Right angle- Hypotenuse-Side(RHS): assuming the hypotenuse and side of one right-calculated triangle are equivalent to the hypotenuse and the comparing side of another right-calculated triangle, the two triangles are consistent.
To know about congruence visit:
brainly.com/question/7888063
#SPJ4
Find the value of the constant m √150 - √12m + √54 = 0
Answers
Answer:
m is √2
Step-by-step explanation:
\({ \tt{ \sqrt{150} - \sqrt{12}m + \sqrt{54} = 0 }} \\ { \tt{ \sqrt{12}m } = \sqrt{150} - \sqrt{54} } \\ { \tt{ (\sqrt{4 \times 3}) m = ( \sqrt{25 \times 6} ) - ( \sqrt{9 \times 6}) }} \\ { \tt{( \sqrt{4 \times 3} )m = 5 \sqrt{6} - 3 \sqrt{6} }} \\ { \tt{2 \sqrt{3}m = 5 \sqrt{6} - 3 \sqrt{6} }} \\ { \tt{2 \sqrt{3} m = 2 \sqrt{6} }} \\ { \tt{ \sqrt{3} m = \sqrt{6} }} \\ { \tt{ \sqrt{3} m = ( \sqrt{3} \times \sqrt{2} ) }} \\ { \tt{m = \sqrt{2} }}\)
Negative air pressure created by an air pump makes a vacuum cleaner able to collect air and dirt into a bag or other container. Below are several readings from a pressure gauge. Write rational numbers to represent each of the readings, and then order the rational numbers from least to greatest.
Gauge Readings ( pounds per square inch )
25 psi pressure
13 psi vacuum
6.3 psi vacuum
7.8 psi vacuum
1.9 psi vacuum
2 psi pressure
7.8 psi pressure
Pressure readings ( pounds per inch) answers:
Answers
The ordered rational numbers representing the gauge readings from least to greatest are 19/10, 63/10, 78/10, 78/10, 13/1, 25/1, 2/1.
To represent the gauge readings as rational numbers, we can express them as fractions with a common denominator.
Given readings:
25 psi pressure
13 psi vacuum
6.3 psi vacuum
7.8 psi vacuum
1.9 psi vacuum
2 psi pressure
7.8 psi pressure
Expressed as rational numbers with a common denominator:
25 psi = 25/1
13 psi = 13/1
6.3 psi = 63/10
7.8 psi = 78/10
1.9 psi = 19/10
2 psi = 2/1
7.8 psi = 78/10
Now, let's order these rational numbers from least to greatest:
1.9 psi = 19/10
6.3 psi = 63/10
7.8 psi = 78/10
7.8 psi = 78/10
13 psi = 13/1
25 psi = 25/1
2 psi = 2/1
Ordered from least to greatest:
19/10, 63/10, 78/10, 78/10, 13/1, 25/1, 2/1
Therefore, the ordered rational numbers representing the gauge readings from least to greatest are 19/10, 63/10, 78/10, 78/10, 13/1, 25/1, 2/1.
for such more question on rational numbers
https://brainly.com/question/19079438
#SPJ8
what is the quotient of 1 and 2/3 divided by 4/5
Answers
Answer:
2 and 1/12
Step-by-step explanation:
1 and 2/3 = 5/3.
when dividing fractions, invert and multiply.
5/3x5/4=25/12
=2 and 1/12
Answer:
The quotient is:
2 and 1/12
Step-by-step explanation:
1 and 2/3 = 1 + 2/3
1 = 3/3
1 + 2/3 = 3/3 + 2/3 = (3+2)/3 = 5/3
1 and 2/3 divided by 4/5 is:
(5/3) / (4/5) = (5*5) / (3*4) = 25/12
25/12 = 24/12 + 1/12 = 2 + 1/12 = 2 1/12 = 2 and 1/12
Dean's savings account started with $100. After one year, it had $110. The
second year, it had $121. The third year it had $133.10.
Is a single linear model a reasonable option for this data? Yes or No?
Answers
The statement that answers the linear model possibility is NO
How to determine the true statementFrom the question, we have the following parameters that can be used in our computation:
Initial = 100
Year 1 = 110
year 2 = 121
year 3 = 133.10
The savings account balance is increasing at an inconsistently increasing rate, which is not linear.
The savings account starts with $100, and increases by $10 in the first year, by $11 in the second year, and by $12.10 in the third year.
This is an example of exponential growth, which cannot be modeled by a single linear equation.
Read more about linear models at
https://brainly.com/question/8609070
#SPJ1
(a) Find absolute maximum value of the function f (x, y) = x^3 − xy − y^2 + 2y +1 on the triangle region T with vertices (0, 0), (0, 4) and (4, 6) .
(b) Find absolute maximum value of the function f (x, y) = x^3 − y^2 + 1 on the region R = {(x, y) : x^2/4 + y^2 ≤ 1, y ≥ 0}.
Answers
The absolute maximum value of the function f(x, y) = x³ − y² + 1 on the region R = {(x, y) : x²/4 + y² ≤ 1, y ≥ 0} is 11, achieved at the point (2, 0).
To find the absolute maximum value of a function over a given region, we can follow these steps:
(a) Find the absolute maximum value of the function f(x, y) = x³ − xy − y² + 2y + 1 on the triangle region T with vertices (0, 0), (0, 4), and (4, 6).
Step 1: Find critical points in the interior of the triangle T.
To find critical points, we need to find the partial derivatives of f(x, y) with respect to x and y and set them equal to zero.
∂f/∂x = 3x² - y
∂f/∂y = -x - 2y + 2
Setting ∂f/∂x = 0 and ∂f/∂y = 0 simultaneously, we get:
3x² - y = 0 ...(1)
-x - 2y + 2 = 0 ...(2)
Solving equations (1) and (2) simultaneously, we can find the critical point (x_c, y_c).
From equation (1), we have y = 3x².
Substituting y = 3x² into equation (2), we get:
-x - 2(3x²) + 2 = 0
Simplifying further:
-6x² - x + 2 = 0
We can solve this quadratic equation to find the values of x. However, this equation does not have rational solutions. By using numerical methods or a calculator, we find two approximate solutions for x: x ≈ -0.704 and x ≈ 0.476.
Substituting these values of x into y = 3x², we can find the corresponding values of y_c:
For x ≈ -0.704, y ≈ 1.568.
For x ≈ 0.476, y ≈ 0.649.
So we have two critical points: (x_c, y_c) ≈ (-0.704, 1.568) and (x_c, y_c) ≈ (0.476, 0.649).
Step 2: Evaluate the function f(x, y) at the critical points and at the vertices of the triangle T.
We need to find the function values at the critical points and the vertices of the triangle T.
For the critical points:
f(-0.704, 1.568) ≈ (-0.704)³ - (-0.704)(1.568) - (1.568)² + 2(1.568) + 1 ≈ 2.224
f(0.476, 0.649) ≈ (0.476)³ - (0.476)(0.649) - (0.649)² + 2(0.649) + 1 ≈ 1.445
For the vertices of the triangle T:
f(0, 0) = (0)³ - (0)(0) - (0)² + 2(0) + 1 = 1
f(0, 4) = (0)³ - (0)(4) - (4)² + 2(4) + 1 = 9
f(4, 6) = (4)³ - (4)(6) - (6)² + 2(6) + 1 = -23
Step 3: Compare the function values to find the absolute maximum value.
Comparing the function values, we find that the absolute maximum value of f(x, y) = x³ − xy − y² + 2y + 1 on the triangle region T is 9, which occurs at the vertex (0, 4).
(b) Find the absolute maximum value of the function f(x, y) = x³ − y² + 1 on the region R = {(x, y) : x^2/4 + y² ≤ 1, y ≥ 0}.
Step 1: Find critical points in the interior of the region R.
To find critical points, we need to find the partial derivatives of f(x, y) with respect to x and y and set them equal to zero.
∂f/∂x = 3x²
∂f/∂y = -2y
Setting ∂f/∂x = 0 and ∂f/∂y = 0 simultaneously, we get:
3x² = 0 ...(1)
-2y = 0 ...(2)
From equation (1), we have x = 0.
From equation (2), we have y = 0.
So the only critical point in the interior of the region R is (x_c, y_c) = (0, 0).
Step 2: Evaluate the function f(x, y) at the critical point and at the boundary of the region R.
We need to find the function values at the critical point (0, 0) and at the boundary of the region R.
For the critical point:
f(0, 0) = (0)³ - (0)² + 1 = 1
For the boundary of the region R:
We have x²/4 + y² = 1. Since y ≥ 0, we can rewrite it as y = √(1 - x²/4).
Substituting y = √(1 - x²/4) into f(x, y), we get:
g(x) = x³ - (1 - x²/4) + 1
Expanding and simplifying further, we have:
g(x) = x³ + x²/4 + 1
To find the maximum value of g(x) on the interval [-2, 2], we can take its derivative and set it equal to zero:
g'(x) = 3x²/4 + x/2
Setting g'(x) = 0, we have:
3x²/4 + x/2 = 0
Multiplying through by 4 to clear the fraction, we get:
3x² + 2x = 0
Factorizing, we have:
x(3x + 2) = 0
So the critical points of g(x) are x = 0 and x = -2/3.
Now, we need to evaluate g(x) at the critical points and endpoints of the interval [-2, 2]:
g(-2) = (-2)³ + (-2)²/4 + 1 = -7
g(0) = (0)³ + (0)²/4 + 1 = 1
g(2) = (2)³ + (2)²/4 + 1 = 11
g(-2/3) = (-2/3)³ + (-2/3)²/4 + 1 ≈ 1.741
Step 3: Compare the function values to find the absolute maximum value.
Comparing the function values, we find that the absolute maximum value of f(x, y) = x³ − y² + 1 on the region R is 11, which occurs at the point (2, 0) on the boundary of the region R.
Therefore, the absolute maximum value of the function f(x, y) = x³ − y² + 1 on the region R = {(x, y) : x²/4 + y² ≤ 1, y ≥ 0} is 11, achieved at the point (2, 0).
To know more about absolute maximum check the below link:
https://brainly.com/question/31585459
#SPJ4
find the value of x
-3=16-x
Answers
Answer:
Step-by-step explanation:I don't say you have to mark my ans as brainliest but if you think it has really helped you plz don't forget to thank me...

Expand and simplify 5(y - 2) + 2(y - 3)
Answers
The expression is expanded and simplified to 7y - 4
How to simply the expressionNote that algebraic expressions are described as mathematical expressions that are composed of coefficients, factors, constants, variables and terms.
They are also made up of some mathematical operations. These operations are;
SubtractionAdditionBracketParenthesesMultiplicationDivisionFrom the information given, we have that;
5(y - 2) + 2(y - 3)
expand the bracket, we have;
5y - 10 + 2y - 6
collect the like terms
5y + 2y - 10 + 6
add the values
7y - 4
Learn about algebraic expressions at: https://brainly.com/question/4344214
#SPJ1
A researcher wants to set up a regression equation where Y is a function X. Evaluate the researcher’s options given the following scenarios: (3)
i. Y is I(0); X is I(0)
ii. Y is I(2); X is I(0)
iii. Y is I(1); X is I(1); and the error term is I(0).
Answers
The appropriate regression model depends on the stationarity properties of both the dependent and independent variables, as well as the error term. The researcher can use a standard OLS regression model with first-order differencing of both Y and X.
In the first scenario, both Y and X are I(0), which means they are stationary time series. In this case, the researcher can perform a standard linear regression analysis, as the stationary series would lead to a stable long-run relationship. The answer from this model will be reliable and less likely to suffer from spurious regressions. In the second scenario, Y is I(2) and X is I(0). This implies that Y is integrated of order 2 and X is stationary. In this case, the researcher should first difference Y twice to make it stationary before performing a regression analysis. However, this approach might not be ideal as the integration orders differ, which can lead to biased results.
In the third scenario, Y and X are both I(1) and the error term is I(0). This indicates that both Y and X are non-stationary time series, but their combination might be stationary. The researcher should employ a co-integration analysis, such as the Engle-Granger method or Johansen test, to identify if there is a stable long-run relationship between Y and X. If co-integration is found, then an error correction model can be used for more accurate predictions.
To know more about regression visit:-
https://brainly.com/question/28168620
#SPJ11
Simplify the expression $17x-24x+13x$. Your answer should have the variable $x$ in it only once.
Answers
Answer:
1
Step-by-step explanation:
1+1=2
Click below for more info

Brainliest. follow anything . box of chocolates contains seven milk chocolates and six dark chocolates. Five of the milk chocolates and four of the dark chocolates have peanuts inside. You randomly select a chocolate and eat it. What is the probability it is a dark chocolate with peanuts?
options=2/13, 4/13, 11/13 and 8/13
Answers
Answer:
8/13
Step-by-step explanation:
has the slightly lower numbers meaning 11/13 would be milk chocolate with peanuts, and 8/13 would be the dark chocolate
There are 4 dark chocolate with peanut so
4/13
Last weekend the Lead-X Basketball team ordered fourteen spicy chicken sandwiches
and six chicken bites for fifty-five dollars and ninety cents. This weekend, the team
ordered seven spicy chicken sandwiches and five chicken bites for thirty-three dollars
and nineteen cents.
Answers
From the first order:
14x + 6y = 55.90
From the second order:
7x + 5y = 33.19
We can use elimination method to solve for one of the variables. Multiplying the second equation by 2:
14x + 10y = 66.38
14x + 6y = 55.90
Subtracting the second equation from the first:
4y = 10.48
y = 2.62
Now we can substitute y = 2.62 into either equation to find x:
14x + 6(2.62) = 55.90
14x + 15.72 = 55.90
14x = 40.18
x = 2.87
Therefore, a spicy chicken sandwich costs $2.87 and a chicken bite costs $2.62.
Write the rational number 36/5 as a decimal
Answers
Answer:
36/5 as a decimal is 7.2
Step-by-step explanation:
In the fraction 36/5, 36 is the numerator and 5 is the denominator, the fraction bar means "divided by". Therefore, the fraction 36/5 is same as "36 divided by 5" or "36 ÷ 5".
When we calculated 36 divided by 5, we found that 36/5 in decimal form is:
36 ÷ 5 = 7.2
Therefore, the decimal form of 36/5 is 7.2
Only answer if your are 100% sure.
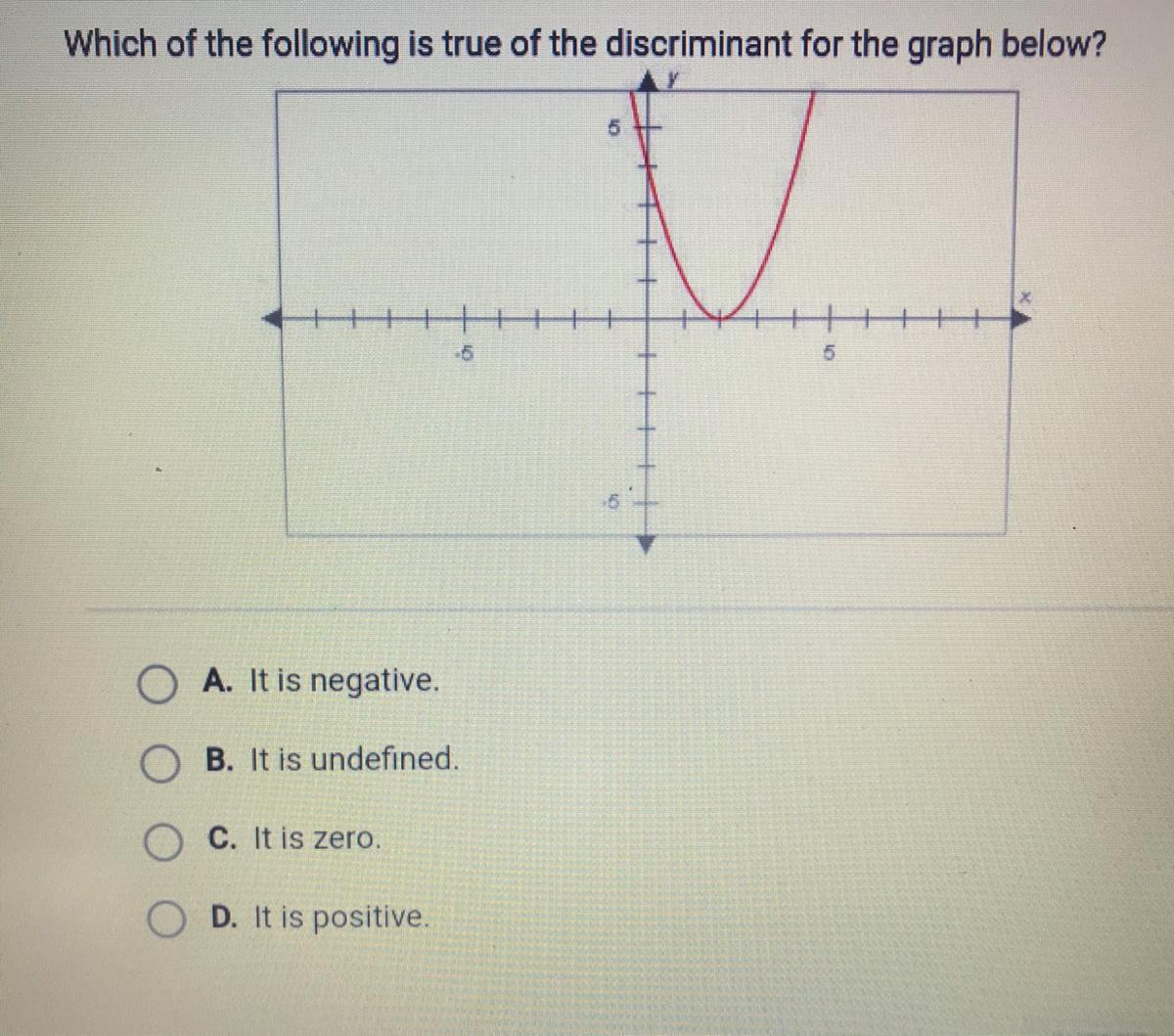
Answers
Answer:
It is zero
Step-by-step explanation:
The attatched should help you understand discriminants:

Answer:C
Step-by-step explanation:
If the discriminant is negative you will have no real roots, if it is positive it will have 2 real roots, only with a discriminant of 0 will you get only one real root. Also, for undefined discriminant that is the same as a negative answer.
it is known that a certain kind of algae in the dead sea can double in population every 4 days. suppose that the population of algae grows exponentially, beginning now with a population of 3,000,000. (a) how long it will take for the population to quadruple in size? days (b) how long it will take for the population to triple in size? days
Answers
Since the algae grow exponentially with doubling time of 4 days, then the population will be quadruple in size in 8 days and will be triple in size in 6.34 days.
The easiest way is to consider the situation as a geometric sequence. If the population doubles its size in 4 days, then it will be quadruple in:
2 x 4 days = 8 days.
In general, we can use the growth formula:
P(t) = Po . 2^(t/Td)
Where:
P(t) = population at time t
Po = initial population
Td = doubling time
Parameters given:
Td = 4 days
P(t) = 3Po
Plug those parameters into the formula:
3 Po = Po . 2^(t/4)
3 = 2^(t/4)
log 3 = (t/4) log 2
t = 4 . log 3 / log 2 = 6.34 days.
Learn more about growth formula here:
https://brainly.com/question/27161222
#SPJ4
Select the set of measurements that can form a triangle.
A. 35°, 150, 130°
B. 90°, 90°, 7 inches
C. 709, 70°, 70°
D. 17 inches, 8 inches, 2 inches
Answers
Answer:
B
Step-by-step explanation:
Suppose you have a coin with P[H] = p. You toss it n times and get
a sequence x1, . . . , xn. Write down the likelihood as a function of p.
Give the max-likelihood estimate for p.
use the notation that 1 denotes H and 0 denotes T
Answers
The likelihood function for a sequence of coin tosses x1, . . . , xn with P[H] = p is given by:
L(p) = P(x1, . . . , xn | p) = P(x1 | p) * P(x2 | p) * . . . * P(xn | p)
Using the notation that 1 denotes H and 0 denotes T, we can write the likelihood function as:
L(p) = p^k * (1-p)^(n-k)
where k is the number of heads in the sequence and n-k is the number of tails.
To find the maximum likelihood estimate for p, we need to take the derivative of L(p) with respect to p and set it equal to zero:
dL(p)/dp = k*p^(k-1)*(1-p)^(n-k) - (n-k)*p^k*(1-p)^(n-k-1) = 0
Solving for p, we get:
p = k/n
Therefore, the maximum likelihood estimate for p is the number of heads in the sequence divided by the total number of tosses.
To learn more about likelihood estimate here:
https://brainly.com/question/29853584#
#SPJ11
If LMU student heights are approximately normal with a mean of 65 inches, and a standard deviation of 2 inches, what is the probability that a randomly selected student would have a height > 68 inches?
Answers
The probability that a randomly selected LMU student would have a height greater than 68 inches is 0.0668 or 6.68%.
To determine the probability that a randomly selected LMU student would have a height greater than 68 inches, you can use the standard normal distribution.
The standard normal distribution is a normal distribution with a mean of 0 and a standard deviation of 1. To convert the given normal distribution with mean 65 inches and standard deviation 2 inches to the standard normal distribution, you can use the formula: z = (x - μ) / σ
where z is the z-score, x is the value you want to convert, μ is the mean, and σ is the standard deviation.Using this formula, you can find the z-score corresponding to a height of 68 inches as follows: z = (68 - 65) / 2 = 1.5. The probability of a randomly selected student having a height greater than 68 inches can be found by looking up the area to the right of the z-score of 1.5 in the standard normal distribution table. The table gives the area to the left of the z-score, so to find the area to the right of the z-score, you can subtract the area to the left from 1: P(z > 1.5) = 1 - P(z < 1.5)
Using the standard normal distribution table, you can find that the area to the left of the z-score of 1.5 is 0.9332. Therefore, the area to the right of the z-score is 1 - 0.9332 = 0.0668 or 6.68%.
Thus, the probability that a randomly selected LMU student would have a height greater than 68 inches is 0.0668 or 6.68%.
To know more about probability, click here
https://brainly.com/question/32117953
#SPJ11
A bakery owner wants to keep his bakery open a few more hours every evening. He wants to conduct a survey to determine whether extending the bakery's hours would be what costumers want. Which survey method would likely produce the most representative sample?
Answers
Answer:
Ask every tenth customer over the period of a week.
Step-by-step explanation:
Required
Select which of the options is true
(a) Every 5th male customer
This method will not produce a correct representative sample because only the male customers are surveyed. The opinion of the female customers will not be represented in the sample
(b) Every customer after 5:00pm
This method will not produce a correct representative sample because only the customers who come to the bakery before 5:00pm will not be represented. The opinion of these customers will not be represented in the sample
(c) Every 10th customer over the week
This method will produce a correct representative sample because the opinions of the customers are taken, irrespective of the gender or the time the customer walks into the bakery.
It's believed that as many as 21% of adults over 50 never graduated from high school. We wish to see if this percentage is the same among the 25 to 30 age group. a) How many of this younger age group must we survey in order to estimate the proportion of non-grads to within 10% with 90% confidence? n= (Round up to the nearest integer.)
Answers
A minimum sample size of 121 individuals needs to be surveyed, ensuring a rounded-up value to estimate the proportion of non-graduates within the 25 to 30 age group with a 10% margin of error and 90% confidence.
To determine the sample size required to estimate the proportion of non-graduates within the 25 to 30 age group with a certain level of confidence and margin of error, we can use the formula:
n = (Z^2 * p * (1 - p)) / E^2
Where:
n is the required sample size
Z is the Z-score corresponding to the desired confidence level (90% confidence corresponds to a Z-score of approximately 1.645)
p is the estimated proportion of non-graduates (0.21 based on the information provided)
E is the desired margin of error (10% or 0.10)
Substituting the values into the formula:
n = (1.645^2 * 0.21 * (1 - 0.21)) / 0.10^2
n ≈ 120.41
Rounding up to the nearest integer, the required sample size is 121.
Therefore, you would need to survey at least 121 individuals in the 25 to 30 age group to estimate the proportion of non-graduates within 10% margin of error with 90% confidence.
To know more about sample size refer here:
https://brainly.com/question/30100088#
#SPJ11
what is the area of the following circle

Answers
Answer: 25 pi
Step-by-step explanation:
i just need the answers no need to explain

Answers
Answer:
1. A
2. C
3. A
Step-by-step explanation: