39. Find the minimized Boolean expression for the functions defined by each of the following truth tables a) x у Z F 0 0 0 X 0 0 1 X 10 1 0 1 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 b) w x y Z F 0 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 1 1 0 0 1 0 0 х 0 1 0 1 0 0 1 1 0 X 0 1 1 0 1 10 0 0 1 1 0 D 1 X 1 10 1 0 х 1 0 1 1 X 1 1 0 0 X 1 1 0 1 1 1 1 1 0 X 1 1 1 X
Answers
The minimized boolean expression for this truth table is:
F = w'x'z + w'yz' + wx' + wxy'zThe given truth table for the function defined by the boolean expression X у Z F is shown below;
x y z F
0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 1
To obtain the minimized expression, we can use Karnaugh maps or Boolean algebra laws like distributivity, commutativity, and associativity to simplify the original expression. However, since the expression is relatively small, we can also obtain the minimized expression by inspection.
The minimized boolean expression for this truth table is:
F = y'z' + xzThe given truth table is:
w x y z F
0 0 0 0 0
0 0 0 1 1
0 0 1 0 0
0 0 1 1 0
0 1 0 0 X
0 1 0 1 0
0 1 1 0 X
0 1 1 1 1
1 0 0 0 1
1 0 0 1 1
1 0 1 0 X
1 0 1 1 1
1 1 0 0 X
1 1 0 1 1
1 1 1 0 X
1 1 1 1 X
Therefore, the minimized boolean expression for this truth table is:
F = w'x'z + w'yz' + wx' + wxy'zLearn more about boolean expression https://brainly.com/question/13265286
#SPJ11
Related Questions
\(\left \{ {{y=2} \atop {x=2}} \right. x_{123}\)
Answers
Answer:
if a joke i dont know
List 2 possible solutions for the inequality x < 9.
Answers
Answer: Any number less than 9.
Step-by-step explanation: The inequality is x is less than 9, that’s what < means, so you can say x is 8, 7, 6, 6.9, etc, x is anything less than 9.
An amoeba divides to form two amoebas after one hour. One hour later, each of the two
amoebas divides to form two more. Every hour, each amoeba divides to form two more.
1. How many amoebas are there after 1 hour?
2. How many amoebas are there after 2 hours?
3. Write an expression for the number of amoebas after 6 hours.
Answers
Step-by-step explanation:
Given that the number of amoeba is 1
in 1 hour it divides to form 2
1 hour later (2 hours): 1 amoeba(forms 2), 1 amoeba(forms 2)= 4
1 hour again(3 hours): 1=2,1=2,1=2,1=2 hence a total of 8 after 3 hours
Question and answers
1. How many amoebas are there after 1 hour
=2 amoebas
2. How many amoebas are there after 2 hours
=4 amoebas
3. Write an expression for the number of amoebas after 6 hours.
let the number of amoeba be y, and the time be n
so in 6 hours n= 6
\(y=2^n\)
\(y= 2^6\\\\y= 64 amoebas\)
A sample of undergraduates at OSU were given an IQ test. The mean was110 and the standard deviation was 10. Draw a sketch of the data.
a. What percent scored below a 90 on the IQ test?
b. What percent scored higher than a 115? Lower than a 115?
c. If you wanted to find the top 15% of students, what would be the cutoffscore?
d. The middle 36% of students fall between what two scores?
e. What percentage of students fall between 95.6 & 105?
Answers
A normal distribution curve with mean 110 and standard deviation 10. Percentages of students scoring below 90, higher than 115, lower than 115, and between IQ score cut offs for the top 15% and the middle 36% of students were 105.7 and 114.3. The percentage of students falling between IQ scores of 95.6 and 105 is 23.5%..
To find the percentage of students who scored below a 90, we need to find the area under the normal distribution curve to the left of 90. Using a standard normal distribution table or calculator, we find that this area is about 0.16 or 16%.
To find the percentage of students who scored higher than a 115, using a standard normal distribution table or calculator, we find that this area is about 0.16 or 16%. To find the percentage of students who scored lower than a 115, we need to find the area under the normal distribution curve to the left of 115, which is about 84%.
To find the IQ score cutoff for the top 15% of students, using a standard normal distribution table or calculator, we find that the z-score is about 1.04. We can then use the formula z = (x - μ) / σ to solve for x, the IQ score cutoff:
1.04 = (x - 110) / 10
x = 121.04
So the IQ score cutoff for the top 15% of students is about 121.04.
To find the IQ scores, using a standard normal distribution table or calculator, we find that the z-scores are about -0.43 and 0.43. We can then use the formula z = (x - μ) / σ to solve for x, the IQ score cutoffs:
-0.43 = (x - 110) / 10
x = 105.7
0.43 = (x - 110) / 10
x = 114.3
So the IQ score cutoffs for the middle 36% of students are about 105.7 and 114.3.
To find the percentage of students who fall between IQ scores of 95.6 and 105, we find that the z-scores are about -1.04 and -0.46. Using a standard normal distribution table or calculator, we find that the area between these z-scores is about 0.235 or 23.5%.
To know more about normal distribution curve:
https://brainly.com/question/15395456
#SPJ4
3. Ura Snob has three times as many dimes as quarters. If he has $2.75, how many quarters
does he have?
Answers
Answer:
75x = 300
x = 4
So he has
4 quarters
3x = 3*4 = 12 dimes
4x = 4*4 = 16 nickels
Step-by-step explanation:
La Michoacana bakery bakes 120 pieces
of sweet bread in 4 hours. At this rate,
how many pieces of sweet bread can be
baked in 12 hours?
PLS HURRY TELL ME
Answers
Answer:
120
Step-by-step explanation:
what is the inequality of 7x-5>-2
Answers
Answer:
x > 3/7
Step-by-step explanation:
7x-5>-2
7x > (-2+5)
x > 3/7
Answer:
x>3/7
Step-by-step explanation:
7x-5>-2 add 5 to both sides
7x>3 divide both sides by 7
x > 3/7
An exam consists of 16 multiple-choice questions. Each of the 16 answers is either right or wrong. Suppose the probability that a student makes fewer than 5 mistakes on the exam is 0.47 and that the probability that a student makes from 5 to 7 (inclusive) mistakes is 0.14. Find the probability of each of the following outcomes.
The probability that a student makes more than 7 mistakes is
Answers
The probability that a student makes more than 7 mistakes on the exam is 0.39.
What is probability all about?In science, the probability of an event is a number that indicates how likely the event is to occur. It is expressed as a number in the range from 0 and 1, or, using percentage notation, in the range from 0% to 100%. T
Now, let X be the number of mistakes a student makes on the exam. Then, the X follows a binomial distribution with n=16 and some unknown probability of success p (i.e., the probability of answering a question correctly).
We know that P(X<5) = 0.47 and P(5<=X<=7) = 0.14. Using the complement rule, we can find P(X>7) as follows:
P(X>7) = 1 - P(X<=7)
= 1 - P(X<5) - P(5<=X<=7)
= 1 - 0.47 - 0.14
= 0.39. Therefore, the probability that a student makes more than 7 mistakes on the exam is 0.39.
Read more about probability
brainly.com/question/24756209
#SPJ1
the data set is made up of these values
Answers
The interquartile range of the set of values given is: 11 - 4 =7
How to find the interquartile rangeTo find the interquartile range, you first begin by defining the lower half, the median, and the upper half. The median of the set of figures given is 8. Then the upper half begins at 11 while the lower half begins and ends at 4.
So, to define the interquartile range, we would subtract 7 from 11 to get 4. So, the interquartile range of the values in the dataset is 4.
Learn more about the interquartile range here:
https://brainly.com/question/4102829
#SPJ1
Complete Question:
A data set is made up of these values 3,4,5,8,9,11,12 Find the interquartile range
find the greatest commom factor gcf for each pair of numbers
9 and 33
Answers
Answer:
3
Step-by-step explanation:
Find the prime factorization of 9
9 = 3 × 3
Find the prime factorization of 33
33 = 3 × 11
To find the GCF, multiply all the prime factors common to both numbers:
Therefore, GCF = 3
The base of a solid S is the region enclosed by the graph of y=√ln(x), x=e, y=0. If the cross section of S perpendicular to the x-axis are squares, determine the volume V, of S.1) 1 cu. units.2) 13(e3−1) cu. units.3) 12 cu.units.4) 23 cu.units.5) 2(e3−1) cu.units.
Answers
The volume V of solid S is e - 1 cubic unit.
What is Volume?
Volume refers to the measure of three-dimensional space occupied by an object or a region. It quantifies the amount of space enclosed by the boundaries of an object or contained within a given region. In mathematical terms, volume is often calculated by integrating the cross-sectional areas of the object or region along a particular axis. Volume is typically expressed in cubic units, such as cubic meters (m^3) or cubic centimeters (cm^3). It is an essential concept in geometry, physics, engineering, and other scientific fields where the measurement of three-dimensional space is involved.
To find the volume of solid S, we need to integrate the areas of the cross sections perpendicular to the x-axis along the interval \([e, \infty).\)
The area of each square cross-section is equal to the square of the side length, which in this case is \(y = \sqrt{\ln(x)}.\)
Therefore, the volume V of solid S can be calculated as:
\(V = \int_{e}^{\infty} (\sqrt{\ln(x)})^2 dx\)
To evaluate this integral, we can simplify the expression:
\(V = \int_{e}^{\infty} \ln(x) dx\)
Using integration by parts, we let \(u = \ln(x)\)and dv = dx:
\(du = \frac{1}{x} dx\\v = x\)
Applying the integration by parts formula:
\(V = [uv] - \int v du= [x \ln(x)] - \int x \left(\frac{1}{x}\right) dx= x \ln(x) - \int dx= x \ln(x) - x + C\)
Evaluating the definite integral:
\(V = [x \ln(x) - x]_{e}^{\infty}= (\infty \cdot \ln(\infty) - \infty) - (e \cdot \ln(e) - e)= \infty - 0 - (1 - e)= e - 1\)
Therefore, the volume V of solid S is e - 1 cubic unit.
To learn more about volume:
https://brainly.in/question/17575802
#SPJ4
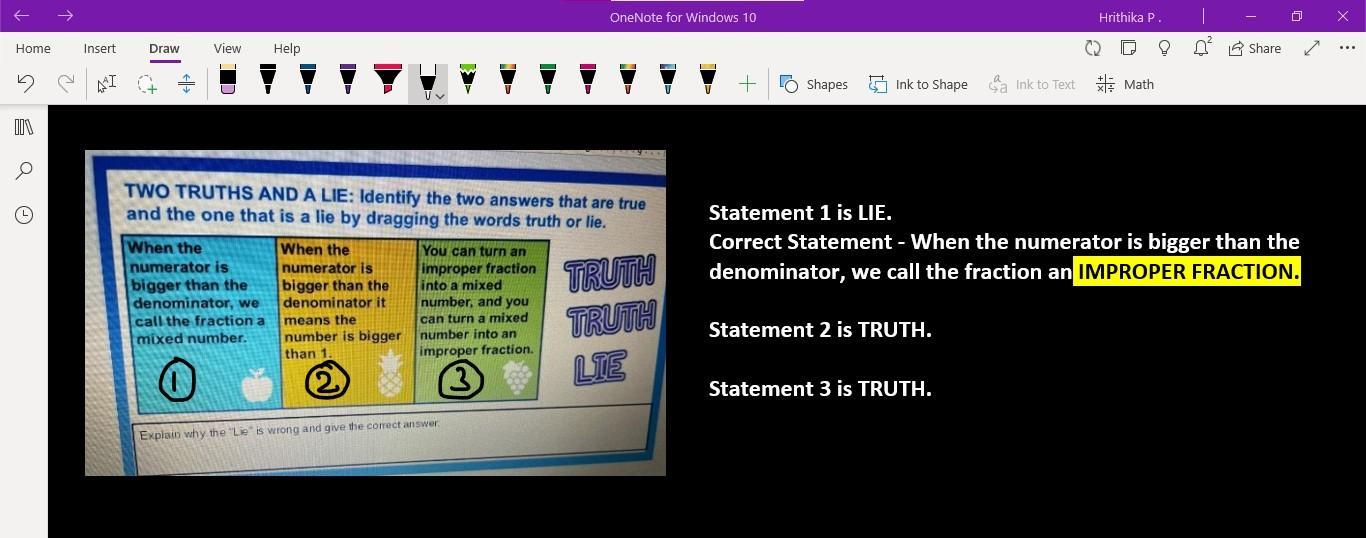
I need to know the answer to this question

Answers
LIE
TRUTH
TRUTH
THE DETAILED ANSWER IS IN THE IMAGE ATTACHED.
HOPE IT HELPS YOU......
PLEASE MARK AS BRAINLLIEST!!!
In centimeters, what is the unknown length in this right triangle?
61 cm
60 cm
Answers
Answer:11
Step-by-step explanation:
suppose that you are rolling a six sided dice. let a = even what is p(ac)?
Answers
Answer:
1/2
Step-by-step explanation:
When you roll a 6-sided die, there are 6 possible outcomes:
1, 2, 3, 4, 5, 6
3 of the outcomes are even, and 3 of the outcomes are odd.
p(A) = p(even) = 3/6 = 1/2
p(Ac) = 1 - p(A) = 1 - 1/2 = 1/2
Richard Gaziano is a manager for Health Care, Inc. Health Care deducts Social Security, Medicare, and FIT (by percentage method) from his earnings. Assume a rate of 6.2% on $118,500 for Social Security and 1.45% for Medicare. Before this payroll, Richard is $1,000 below the maximum level for Social Security earnings. Richard is married, is paid weekly, and claims 2 exemptions. What is Richard’s net pay for the week if he earns $1,700?
Answers
Richard's net pay for the week, considering Social Security, Medicare, and FIT deductions, can be calculated by subtracting the total deductions from his gross earnings.
First, let's determine the amount deducted for Social Security. The Social Security rate is 6.2%, and the maximum earnings subject to this deduction are $118,500. Since Richard is $1,000 below the maximum level, the amount subject to Social Security deduction is $1,000. Therefore, the Social Security deduction is 6.2% of $1,000.
Next, we calculate the Medicare deduction. The Medicare rate is 1.45%, and it is applied to the entire earnings of $1,700.
To calculate the FIT deduction, we need additional information about Richard's taxable income, tax brackets, and exemptions. Without this information, we cannot provide an accurate calculation for the FIT deduction.
Finally, we subtract the total deductions (Social Security, Medicare, and FIT) from Richard's gross earnings of $1,700 to obtain his net pay for the week.
Learn more about subtract here: brainly.com/question/28008319
#SPJ11
The circumference
of the circle shown above
is 108. The length of the minor arc AB is a pi. What is the value of a
Answers
Answer:
Thus, the length of the arc AB will be 5/18 of the circumference of the circle, which equals 2πr, according to the formula for circumference. length of arc AB = (5/18)(2πr) = (5/18)(2π(18)) = 10π. Thus, the length of arc AB is 10π.
Step-by-step explanation:
If there are 16 people in a hospital and 4 need an xray.
What is the probabilty that if you choose 2 people randomly, exactly one will need an xray?
Answers
The probability that if you choose 2 people randomly, exactly one will need an x-ray is 0.4.
The probability that if you choose 2 people randomly from the 16 in the hospital, exactly one will need an x-ray is as follows:
Firstly, calculate the probability of choosing one person who needs an X-ray and one person who doesn't.
There are 4 people who need an x-ray and 12 who don't, so the probability for this is (4/16) * (12/15).
Now, calculate the probability of choosing one person who doesn't need an X-ray and one person who does. This is (12/16) * (4/15).
Now, add the probabilities to find the total probability.
The probability that exactly one person will need an x-ray is
(4/16) * (12/15) + (12/16) * (4/15) = 2/5
=0.4.
Learn more about probability:
https://brainly.com/question/251701
#SPJ11
The probability that if you choose 2 people randomly, exactly one will need an x-ray is 0.4 or 40%.
If there are 16 people in a hospital and 4 need an xray, the probability that if you choose 2 people randomly, exactly one will need an xray is 0.56.
Total number of people in a hospital = 16
Number of people who need an x-ray = 4
Thus, the probability that if you choose 2 people randomly, exactly one will need an x-ray is given by;
P(one needs an x-ray) = (Number of people who need an x-ray × Number of people who do not need an x-ray) / Total number of people × Total number of people - 1
P(one needs an x-ray) = (4 × 12) / 16 × 15
P(one needs an x-ray) = 0.08
P(one doesn't need an x-ray) = (Number of people who need an x-ray × Number of people who do not need an x-ray) / Total number of people × Total number of people - 1
P(one doesn't need an x-ray) = (12 × 4) / 16 × 15
P(one doesn't need an x-ray) = 0.32
Now, we have to add both the probabilities of exactly one person needing an x-ray and exactly one person not needing an x-ray;
P(exactly one person needs an x-ray) = P(one needs an x-ray) + P(one doesn't need an x-ray)
P(exactly one person needs an x-ray) = 0.08 + 0.32P(exactly one person needs an x-ray) = 0.4
The probability that if you choose 2 people randomly, exactly one will need an x-ray is 0.4 or 40%.
learn more about 'probability'
#SPJ11
what point satisfies the inequality of Y < -4x + 3 and indicates side of the inequality should be shaded
Answers
First, we plot the graph of the equation y=-4x+3, to do this, we only need two points
\(\begin{gathered} x=0\text{ , y=-4(0)+3=3} \\ (0,3) \\ x=1,\text{ y=-4(1)+3=-1} \\ (1,-1) \end{gathered}\)In green it is shaded the ponts that satisfy the inequality, that is because the y value must be below (that's why it has the sigh <) this graph.

I NEED HELP d) If (m²-1)/m = 6, find the values of (i) m² + 1/m²

Answers
Answer:
(6m² + 12m + 2) / (6m + 1)
Step-by-step explanation:
multiply both sides by m.
we get m² - 1 = 6m
move the -1 to the other side, so it becomes +1
m² = 6m + 1
so m² + 1/m² = (6m + 1) + 1/(6m + 1)
get a common denominator by squaring (6m + 1)
(6m + 1)².
we now have (6m + 1)² / (6m + 1) + 1/(6m + 1).
we now add the numerators.
(6m + 1)² + 1 = (6m² + 6m + 6m + 1) + 1 = 6m² + 12m + 2.
numerator over denominator = (6m² + 12m + 2) / (6m + 1)
There is a number(y), divided by 9, gets a remainder of 8. Divide y by 8, and you get a remainder of 7. Divide y by 7, you get a remainder of 6. Divide y by 6, you get a remainder of 5. Divide y by 5, you get a remainder of 4. Divide y by 4, you get a remainder of 3. Divide y by 2, you get a remainder of 1. What is the value of y? Show work.
Answers
The value of y can be an infinite number of answers such as 1,2,3,4,5,6,7,8,9 ......n(infinity)
How to determine and prove that y is an infinite number?Let's go with the first statement;
If y = 1
Then ; 1× 9 = 9+ 8 = 17÷ 9 = 1 remainder 8
If y = 2 2 × 9 = 18+8 = 26÷9 = 2 remainder 8
If y= 3 3×9 = 27+8 = 35÷9 = 3 remainder 8
For the second statement;
If y = 1
Then; 1×8 = 8+7 = 15/8 = 1 remainder 7
If y = 2 2×8 = 16+7 = 23/8 = 2 remainder 7
For third statement;
If y = 1
Then; 1×7 = 7+6 = 13/6 = 1 remainder 5
For fourth statement;
if y = 1
Then; 1×6 =6+5 = 11/6 = 1R5
For fifth statement;
If y = 1
Then; 1×5 = 5+4 = 9/5= 1R4
For sixth statement;
if y = 1
Then ; 1×4 = 4+3 = 7/4 = 1R3
For seventh statement;
if y = 1
Then ; 1×3= 3+2 = 5/3 = 1R2
For eight statement;
if y = 1
Then; 1×2 = 2+1 = 3/2 = 1R1
Learn more about infinite here:
https://brainly.com/question/30764572
#SPJ1
50 points and brainliest be fast pls
Find the length of the base of a triangle if one side is 3 cm longer than the base, and the other side is 5 cm shorter than the base. The perimeter of the triangle is 52 cm.
Answers
Answer:
base of triangle is 18 cm
Step-by-step explanation:
Perimeter of triangle: P = a + b + c
if a is the base
then b = a + 3
and c = a - 5
so a + b + c = P
a + (a + 3) + (a - 5) = 52
3a - 2 = 52
3a = 54
a = 54/3 = 18
A value meal package at Ron's Subs consists of a drink, a sandwich, and a bag of chips. There are 6 types of drinks to choose from, 3 types of sandwiches, and 4 types of chips. How many different value meal packages are possible?
Answers
Analyze the proportion below and complete the instructions that follow.
2x+5 x-5
3
4
Solve the proportion for x
A. -7
B. -4
C-2
D. -1
Answers
Answer:
A
Step-by-step explanation:
(2x + 5)/(3) = (x - 5)/(4)
Multiplying both sides by 12 to eliminate the fractions, we get:
4(2x + 5) = 3(x - 5)
Expanding the brackets, we get:
8x + 20 = 3x - 15
Subtracting 3x and 20 from both sides, we get:
5x = -35
Dividing both sides by 5, we get:
x = -7
Therefore, the solution to the proportion is x = -7.
So, the correct option is A) -7.
a telephone call center uses two customer service representatives (csrs) during the 8:30 a.m. to 9:00 a.m. time period. the standard service rate is 2.0 minutes per telephone call per csr. assuming a target labor utilization rate of 70 percent, how many calls can these two csrs handle during this half-hour period? round your answer to the nearest whole number.
Answers
A telephone call center uses two customer service representatives (csrs) during the 8:30 a.m. to 9:00 a.m. time period. the standard service rate is 2.0 minutes per telephone call per csr. assuming a target labor utilization rate of 70 percent, Therefore, these two CSRs can handle approximately 3 calls during this half-hour period.
Given a telephone call center uses two customer service representatives (CSRs)
during the 8:30 a.m. to 9:00 a.m. time period, and the standard service rate is 2.0 minutes per telephone call per CSR. Assuming a target labor utilization rate of 70%,
we have to determine the number of calls these two CSRs can handle during this half-hour period.
The formula to calculate the number of calls that can be handled during this half-hour period is:
Number of calls = (number of servers x utilization rate x service time) / arrival rate
= (2 x 0.70 x 2) / 1
= 2.8 calls (rounded to the nearest whole number)
Therefore, these two CSRs can handle approximately 3 calls during this half-hour period.
for such more question on calls
https://brainly.com/question/29497021
#SPJ11
Heights, in inches, for the 200 graduating seniors from Washington High School are summarized in the frequency table below.
Which of the following statements about the median height is true?
answer choices
It is greater than or equal to 72 inches but less than 78 inches.
It is greater than or equal to 66 inches but less than 72 inches.
It is less than 60 inches.
It is greater than or equal to 60 inches but less than 66 inches.
Answers
Option (D), the last option is the correct statement, If heights in inches of 200 graduating seniors were summarized in the frequency table;
The median height is greater than or equal to 60 inches but less than 66 inches.
The median is the number value that separates the lower and upper values to halves. The median height is determined by arranging all the given heights in order either from the smallest to highest or from highest to smallest without skipping any measurement of the heights.
After arranging all the heights in order, the median height is usually at the middle.
The reason as to why the median height is greater than or equal to 60 inches but less than 66 inches is because the middle height should not be same as the largest height of 66 inches. It is possible to have multiple 60 inch heights from the 200 seniors. It is also possible to have multiple 66 inch of heights from the 200 seniors.
To learn more about median, use the link below:
brainly.com/question/28060453
#SPJ4
A forest contains 24 elk, of which, 8 are captured, tagged, and released. a certain time later, 4 of the 24 elk are captured. what is the probability that 3 of these 4 have been tagged?
Answers
The probability that 3 out of the 4 captured elk have been tagged is approximately 0.0053.
To solve this problemWe can use the concept of combinations.
The total number of ways to choose 4 elk out of 24 is given by the combination formula:
C(24, 4) = 24! / (4!(24-4)!) = 10,626
Now, we need to consider the number of ways to choose 3 tagged elk out of the 8 tagged elk and 1 untagged elk. The number of ways to do this is given by:
C(8, 3) * C(1, 1) = 8! / (3!(8-3)!) * 1! / (1!(1-1)!) = 56
Therefore, the probability that 3 out of the 4 captured elk have been tagged is:
P = (Number of ways to choose 3 tagged elk out of 8 tagged elk and 1 untagged elk) / (Total number of ways to choose 4 elk out of 24)
P = 56 / 10,626
Calculating this division gives us the probability:
P ≈ 0.0053
So, the probability that 3 out of the 4 captured elk have been tagged is approximately 0.0053 .
Learn more about concept of combinations here : brainly.com/question/4658834
#SPJ4
The end points of AB are A (3.-8) and B(1,2). Find the midpoint, M, of AB.
Answers
Answer:
Step-by-step explanation:
(3+1)/2= 4/2 = 2
(-8+2)/2= -6/2= -3
(2, -3)
Find the missing side length, and enter your answer in the box below. If
necessary, round your answer to 2 decimal places.
9
12

Answers
use the Pythagorean Theorem for these problems.
Let xy=3 and dy/dt=4. Find dx/dt when x=5
Answers
Answer:
xy = 3
d/dt(xy) = d/dt(3)
ydx/dt + xdy/dt = 0
y = 3/x so substitute 3/5 for y, 5 for x, and 5 for dy/dt; and solve for dx/dt.
3/5(dx/dt) + 5(5) = 0
3/5(dx/dt) = -25
dx/dt = -125/3
Step-by-step explanation:
this should be able to help you :)
What is the solution to 6(n−2)−8=22+4(2−n)?
Answers
Answer:
n=5
Step-by-step explanation:
6(n-2)-8=22+4(2-n)
open brackets
6n-12-8=22+8-4n
collect like terms
6n+4n=22+8+12+8
10n=50
n=50/10
n=5