37. The sum of first three terms in an arithmetic progression is 24 and the sum of their squares is 224. Find the first three terms of this arithmetic progression.
Answers
Answer:
12, 8, and 4
Step-by-step explanation:
Givena + d + a + a - d = 24
3a = 24 ⇒ [ a = 8 ]
and (a + d)² + a² + (a - d)² = 224
3a² + 2d² = 224
2d² = 224 - 192 = 32
d² = 16
[ d = ±4 ]
∴ The first three terms to A.P are
a + d = 8 + 4 = 12
a - = 8
a - d = 8 - 4 = 4
∴ Three terms are 12 , 8, and 4
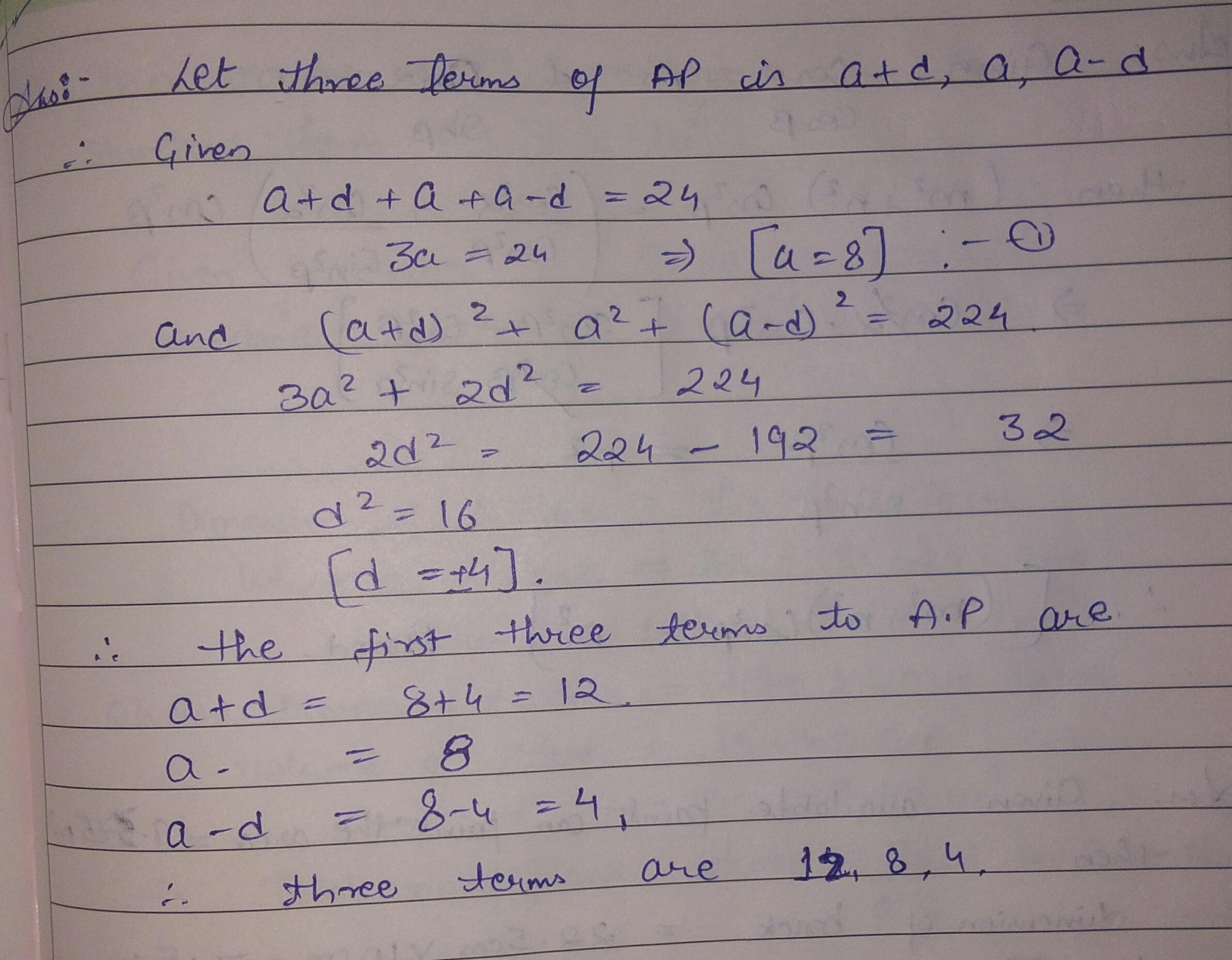
Related Questions
Kevin bought twelve 8-ounce bottles of water. How many milliliters of water did Kevin buy? (Note: 1 ounce ≈ 30 ml) Thank you for any help I may get! <3
Answers
Given:
Kevin bought twelve 8-ounce bottles of water.
1 ounce ≈ 30 ml
To find:
The quantity of water in milliliters
Solution:
We have,
1 ounce ≈ 30 ml
8 ounce ≈ 8×30 ml
8 ounce ≈ 240 ml
It means, one 8 ounce bottle can hold about 240 milliliters of water.
Total number of bottles = 12
So, the quantity of water Kevin buy in milliliters is
\(12\times 240=2880\)
Therefore, Kevin buys 2880 milliliters of water in twelve 8-ounce bottles.
Tina wrote the equations 3 x minus y = 9 and 4 x + y = 5. What can Tina conclude about the solution to this system of equations?
Answers
Answer:
(2, –3) is a solution to the system of linear equations.
Step-by-step explanation:
Given: Equations:
3x - y = 9 --------(1),
4x + y = 5 --------(2),
Add Equation (1) + Equation (2),
3x + 4x = 9 + 5
7x = 14 ( Combine like terms )
x = 2 ( Divide both sides by 7 ),
From equation 1:
3(2) - y = 9
6 - y = 9
-y = 9 - 6 ( Subtraction 6 on both sides )
-y = 3
y = - 3 ( Multiplying -1 on both sides )
Find the length of the third side. If necessary, round to the nearest tenth.
24
ко

Answers
Answer: 26
Step-by-step explanation: The third length is the hypotenuse or the longest side
A scout group is having a cake sale to raise $90 for camping supplies. The troop spent $18 on ingredients for cakes. Cake slices will sell for $1 each. The equation below can be used to find the number of slices of cake the troop needs to sell to raise $90. n−18=90 How many slices of cake does the troop need to sell to raise $90?
Answers
Answer:
N=108
Step-by-step explanation:
You just have to add the $90 they need to raise plus the ingredients price to get $108.
write a polynomial to represent the volume of the rectangular prism if 0.5x-3 and x-4 and x+5
Answers
The polynomial to represent the volume of the rectangular prism is:
V = (0.5x - 3) × (x - 4) × (x + 5)
Simplifying this expression gives V = 0.5x³ - 6.5x² - 23x + 60
How to calculate the volume (V) of a rectangular prism?
The volume (V) of a rectangular prism can be calculated using the formula V = l × w × h, where l, w, and h are the length, width, and height of the prism respectively.
Here, the length (l) can be represented by (0.5x - 3), the width (w) can be represented by (x - 4), and the height (h) can be represented by (x + 5).
Therefore, the polynomial to represent the volume of the rectangular prism is:
V = (0.5x - 3) × (x - 4) × (x + 5)
Simplifying this expression gives V = 0.5x³ - 6.5x² - 23x + 60
To learn more about the volume (V) of a rectangular prism visit:
https://brainly.com/question/24284033
#SPJ9
T/F. Exception reports show a greater level of detail than is included in routine reports.
Answers
True. Exception reports show a greater level of detail than is included in routine reports.
Exception reports are reports that help in identifying data that does not conform to expected patterns. Exception reports show information about an exception in the data set.
This helps to identify irregularities or anomalies in data or system operations.Exception reports are used to analyze system performance, monitor resource consumption, and to detect unusual activity.
This type of report is important to identify issues or errors, where the routine reports or standard reports would not provide enough detail or insight to do so.
It provides detailed information on any unusual event or anomaly that occurred beyond the usual course of events or processes.Exception reports are generated and distributed when the data is not expected or when an event occurs that is outside of what is considered typical.
For example, a financial system might generate an exception report if a transaction is entered that exceeds the maximum allowed amount. This report would show the details of the transaction and highlight the exception.
The purpose of exception reports is to provide users with a higher level of detail than they would find in routine reports. Exception reports are used to highlight significant data, which will be used for further analysis or action.
To learn more about : Exception reports
https://brainly.in/question/50910666
#SPJ8
I NEED HELP I DONT UNDERSTAND IT!! ASAP FOR A TEST
A. ( 4,-3)
B. (-3,4)
C.(-4,3)
D. ( 3,-4)
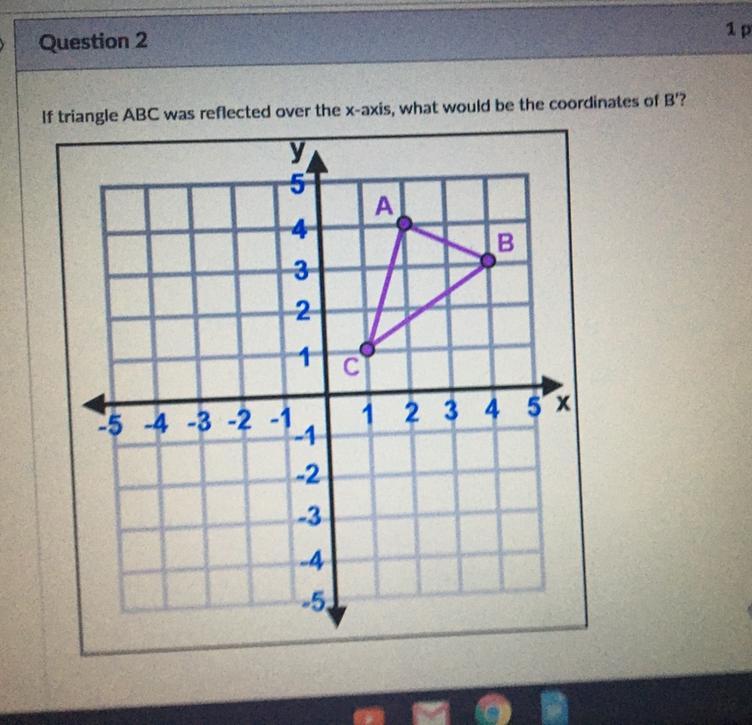
Answers
Because it’s reflected
which number is equavelent to .45

Answers
Answer: ( A )
Step-by-step explanation: basically as the question is what is equivalent to .45 and if you put it like a fraction kinda it will look like this 1\45
yo can somebody help me with this please i really need a good grade ill give crown to




Answers
Answer: 3/4
Step-by-step explanation:
You have to find one single number that goes into both the numerator and the denominator. In this case, it was 8.
24/8 = 3
32/8 = 4
Answer:
1st one is 3/4
second one is 32
I cant really see the third one
fourth one is $1.03
Step-by-step explanation:
Gía trị của x thỏa mãn x2 + 16 = 8x
Answers
Answer:
yes u are correct
Step-by-step explanation:
x2+16=8x
16=6x
16/6=x
x=2.6666666 or 2/3
A toy maker finds that it costs C = 450+ 3.75x dollars to manufacture x toy trucks. If the budget allows $3600 in costs, how many trucks can be made?
Answers
Answer:
840
Step-by-step explanation:
3600=450+3.75x
3600-450=3.75x
3150=3.75x
3150/3.75=x
840=x
840
PLZ PLZ PLZ Help!!! Consider the infinite series defined by

Answers
Answer:
(a)
\(r =\lim_{n \to \infty} |\frac{\frac{2(n+1)!}{2^{2(n+1)}}}{\frac{2n!}{2^{2n}}}| = \lim_{n \to \infty} \frac{n+1}{4} = \infty\)
(b)
if r<1, then it converges absolutely
if r>1, then it diverges
if r=1, then the test is inconclusive
Step-by-step explanation:
The ratio test is:
\(\lim_{n \to \infty} |\frac{x[n+1]}{x[n]}| = L\)
if L<1, then it converges absolutely
if L>1, then it diverges
if L=1, then the test is inconclusive
I'm assuming that they used r instead of L. Anyway, to do the ratio test, you plug in n+1 into the equation and make that numerator.
Then you plug in n into the same equation and make that your denominator.
In our case, our equation is \(\frac{2n!}{2^{2n}}\).
So lets plug in n+1 and make that our numerator.\(\frac{2(n+1)!}{2^{2(n+1)}}\)
Now lets plug in n and make that our denominator. \(\frac{2n!}{2^{2n}}\)
Now set up the ratio test.
\(\lim_{n \to \infty} |\frac{x[n+1]}{x[n]}| = L\)
\(\lim_{n \to \infty} |\frac{\frac{2(n+1)!}{2^{2(n+1)}}}{\frac{2n!}{2^{2n}}}| = L\)
if you simplify this, you would get (view image for the steps)
\(\lim_{n \to \infty} |\frac{\frac{2(n+1)!}{2^{2(n+1)}}}{\frac{2n!}{2^{2n}}}| = \lim_{n \to \infty} \frac{n+1}{4} = \infty\)
L = infinity, which is > 1, therefore this series diverges

(a). The value of r from ratio test is greater than 1.
(b). The value of r tell about that the given series is converges or diverges.
The ratio test is given as,
\(\lim_{n \to \infty} (\frac{x(n+1)}{x(n)} )=r\)
if \(r<1,\) then series converges absolutely
if \(r>1,\) then series diverges
if \(r=1,\) then the test is inconclusive
Given infinite series is,
\(x(n)=\frac{2n!}{2^{2n} }\)
\(\lim_{n \to \infty} \frac{\frac{2(n+1)!}{2^{2(n+1)} } }{\frac{2n!}{2^{2n} } } = \lim_{n \to \infty} \frac{n+1}{4}=\infty=r\)
Here, Observed that value of r is greater than 1.
Thus, the given series is diverges.
Learn more:
https://brainly.com/question/23804543
Jasiah wants to buy a bicycle that costs $330. He has saved $50 so far and will save $40 each week until he has enough money to buy the bicycle
Answers
Working:

Answer:
$280
Step-by-step explanation:
There are 2 ways to do the question.
Method 1: $330-$50=$280
Method 2: 7 days equals to one week=$40.
$40×7=$280
Hope these helps you!
anyone know this??? please help, help!!! thanks!

Answers
Answer:
c. -19
Step-by-step explanation:
Answer:
A
Step-by-step explanation:
Given a polynomial in standard form
The leading coefficient is the coefficient of the variable with the largest exponent.
The term with the largest exponent of the variable is
\(\frac{1}{4}\) \(x^{5}\)
Then the leading coefficient is \(\frac{1}{4}\) → A
4√3 − 5√7 + 2√3 + 6√7
Answers
Answer:
\( \dashrightarrow \: { \tt{4 \sqrt{3} - 5 \sqrt{7} + 2 \sqrt{3} + 6 \sqrt{7} }} \\ \\ \dashrightarrow \: { \tt{(4 - 2) \sqrt{3} + (6 - 5) \sqrt{7} }} \\ \\ \dashrightarrow \: { \tt{2 \sqrt{3} + \sqrt{7} }} \\ \\ \dashrightarrow \: { \tt{ \sqrt{3 \times 4} + \sqrt{7} }} \\ \\ \dashrightarrow \: { \tt{ \sqrt{12} + \sqrt{7} }}\)
Answer:
Step-by-step explanation:
\(4\sqrt{3} - 5\sqrt{7} +2\sqrt{3} +6\sqrt{7}=4\sqrt{3} + 2\sqrt{3} -5\sqrt{7}+6\sqrt{7}\)
\(=(4+2)\sqrt{3}+ (-5 +6)*\sqrt{7}\\\\=6\sqrt{3}+1\sqrt{7}\)
A collection agency specializing in collecting past-due commercial invoices charges $27 as an application fee plus 14% of the amount collected. What is the total charge for collecting $3400 past-due commercial invoices?
a. $503
b. $24
c. $476
d. $270
Solve for rate in the problem. Round to the nearest tenth of a percent.
$980 is ____________% of $1954.
a. 0.5
b. 0.1
c. 50.2
d. 199.4
Supply the missing numbers. Round decimals to the nearest thousandth and percents to the nearest tenth of a percent.
fraction decimal percent
0.583
a. 7/12 58.3%
b. 1/2 58.3%
c. 7/12 5.83%
d. 1/2 5.83%
Answers
$3400 in past-due business invoices will cost you $503 to collect. The correct option is (a) $503. The Percentage is 58.3%. Option (a) 7/12 58.3% is the correct answer.
1) A total of $503 will be charged to collect $3400 in past-due business invoices. A $27 application fee plus 14% of the total amount collected are charged by the chosen collection agency. Let C be the amount charged for collecting $3400 past-due commercial invoices.
Application fee = $27Therefore, the amount collected is: $3400 - $27 = $3373Amount charged for collecting is $27 + 14% of $3373.
Mathematically, it is expressed as: C = $27 + (14% of $3373)
Simplifying, we get: C = $27 + 0.14 × $3373C = $27 + $472.22C = $499.22
Rounding off C to the nearest cent, we get: C ≈ $499.23
Therefore, a total fee of $503 was incurred to recover $3400 in past-due business invoices. Therefore, the correct option is (a) $503.
2) We have to fill in the percentage that fits the blank. We can use the formula for finding the percentage given below: Percentage = (Fraction / 1) × 100Given fraction is 0.583Percentage = (0.583 / 1) × 100Percentage = 58.3%Therefore, option (a) 7/12 58.3% is the correct answer.
More on invoices: https://brainly.com/question/27824461
#SPJ11
HELPP
Solve the equation 15+25=4+6x
Answers
Answer:
x=6
Step-by-step explanation:
Answer: x=6
Explanation:
1. Add: 15+25=40
2.Subtract 4 from each side: 40=4+6x
3.Divide by 6: 36=6x
4. x=6
Question is inside of the picture. Please answer fast. Ill give brainliest if answer correct thank you

Answers
The value of Sin(a + b) = \(-\frac{3+4\sqrt{15} }{20}\) and value of
Cos (a -b) = 119/400
Given,
In the question;
Sin(a) = 1/4 and cos(b) = -3/5
with a and b both in the interval [\(\frac{\pi }{2} ,\pi\))
To find the sin(a + b) and cos (a - b)
Now, According to the question:
We know that :
Sin (b) = \(\sqrt{1-cos^2b}\) = 4/5
Cos (a) = - \(\sqrt{1-sin^2a} = - \frac{\sqrt{15} }{4}\)
∴ Sin(a + b) = Sin(a) Cos(b) + Cos(a) Sin(b)
Sin(a + b) = 1/4. (-3/5) + \(-(\frac{\sqrt{15} }{4} )\) . 4/5
Sin(a + b) = \(-\frac{3+4\sqrt{15} }{20}\)
∴ Cos (a -b) = \(cos^2a -sin^2b\)
Cos (a -b) = \((-\frac{\sqrt{15} }{4} )^2\) - \((\frac{4}{5} )^2\)
Cos (a -b) = 119/400
Hence, The value of Sin(a + b) = \(-\frac{3+4\sqrt{15} }{20}\) and value of
Cos (a -b) = 119/400 .
Learn more about Trigonometric Function at:
https://brainly.com/question/26989297
#SPJ1
5 x (-1/3) do u know
Answers
Answer:
~-1.67
Step-by-step explanation:
Multiply. Note that when you multiply a negative and positive number, your answer will be negative:
5 x (-1/3) = (5 * -1)/3
Multiply, then divide:
5 * -1 = -5
-5/3 = ~-1.67 (rounded to the nearest hundredths).
~
Answer:
-5x/3
It just is, trust me.
Consider the following liquids: d = 0.8146 g/mL 1-pentanol Isopropyl alcohol d=0.7851 g/mL 2-pentanol Hexane You have two unknown samples, each known to be one of the above liquids. a. In determining the density of the first unknown, you weighed a 5.00 mL sample of the d 0.8098 g/mL d 0.660 g/mL liquid, and found the mass to be 3.310 g. What is the identity of the unknown? Explain. b. For the second unknown, a 5.00 mL sample weighed 4.061 g. Based on this data, what can you conclude about the identity of unknown number two? Explain. 3. A perfect cube of jade has a mass of 15.00 g. If jade's density is 3.25 g/ml, determine the edge length of the jade cube.
Answers
The identity of the unknown is hexane, the second unknown is isopropyl alcohol, and the edge length of the jade cube is approximately 1.87 cm.
a. To determine the identity of the first unknown, we can compare the calculated density with the known densities of the liquids. The calculated density can be found by dividing the mass of the sample (3.310 g) by its volume (5.00 mL), giving us a density of 0.6620 g/mL.
Since the calculated density (0.6620 g/mL) is closest to the density of hexane (0.7851 g/mL), it is likely that the first unknown is hexane.
b. To determine the identity of the second unknown, we can use the same approach as in part a. By dividing the mass of the sample (4.061 g) by its volume (5.00 mL), we find the calculated density to be 0.8122 g/mL.
This density is closest to the density of isopropyl alcohol (0.7851 g/mL), so it is likely that the second unknown is isopropyl alcohol.
c. To find the edge length of the jade cube, we can use the formula for the volume of a cube: V = l^3. We know the mass of the cube (15.00 g) and its density (3.25 g/mL), so we can find its volume by dividing the mass by the density:
V = m/d = 15.00 g / 3.25 g/mL = 4.62 mL = 4.62 cm^3
Since the volume is equal to the edge length cubed, we can find the edge length by taking the cube root of the volume:
l = cuberoot(V) = cuberoot(4.62 cm^3) = approximately 1.87 cm.
To know more about volume, here
https://brainly.com/question/28058531
#SPJ4
7X +15 X equals help me please
Answers
7x+15x= 22x
Add the coefficients.
a rectangular piece of cardboard measures 8 cm by 6 cm. what is the perimeter of the piece of cardboard?
Answers
Perimeter = 2(8 cm + 6 cm) = 2(14 cm) = 28 cm. We can calculate it in the following manner.
The perimeter of the rectangular piece of cardboard is the sum of all four sides. Using the given measurements of 8 cm by 6 cm, we can calculate the perimeter as follows:
Perimeter = 2(Length + Width)
Perimeter = 2(8 cm + 6 cm)
Perimeter = 2(14 cm)
Perimeter = 28 cm
Therefore, the perimeter of the rectangular piece of cardboard is 28 cm.
Hi! To calculate the perimeter of a rectangular piece of cardboard with measurements 8 cm by 6 cm, you can use the formula: Perimeter = 2(Length + Width). In this case, the length is 8 cm and the width is 6 cm.
Your answer: Perimeter = 2(8 cm + 6 cm) = 2(14 cm) = 28 cm.
Visit here to learn more about perimeter brainly.com/question/6465134
#SPJ11
Solve 5 (r +9) – 2 (1 - r) = 1.
The solution is r= ????
Answers
Step-by-step explanation:
5(r + 9) - 2(1 - r) = 1
5r + 45 - 2 + 2r = 1
7r + 43 = 1
7r = -42
r = -6.
Answer:
r = -6
Step-by-step explanation:
Given equation,
→ 5(r + 9) - 2(1 - r) = 1
Now the value of r will be,
→ 5(r + 9) - 2(1 - r) = 1
→ 5r + 45 - 2 + 2r = 1
→ 5r + 2r + 43 = 1
→ 7r = 1 - 43
→ 7r = -42
→ r = -42/7
→ [ r = -6 ]
Hence, the value of r is -6.
What is the equation of the quadratic graph with a focus of (6, 0) and a directrix of y = −10?

Answers
Answer:
x2 -12x - 20y = 64
In a company the ratio of men to women i 3:2. 30% of the women are under the age of 30. What fraction of all people in the company are women under age of 30
Answers
6/50 fraction of all people in the company are women under age of 30 In a company where the ratio of men to women i 3:2.
In a company the ratio of men to women 3:2
30% of the women are under the age of 30.
suppose there are 500 people in the company
then 300 are men and 200 are women
30% of 200 = 200*30/100= 60 women are under 30
60/500= 6/50 women are under 30
learn more about of percentage here
https://brainly.com/question/29306119
#SPJ4
i neeed heppppppppppppppppppppppp

Answers
22g+g=1+28
23g=29
g=29/23
You have $910 in your checking account. You have paid $185 in bill's online, which were immediately deducted from your checking account. The following day you withdrew $30 for lunch, bought pants for $43, and purchased a gift card for $15 using your debit card. After, you returned the pants for a full refund. How much is in your checking account?
Answers
Answer:
Therefore, the answer to how much is in the checking account is $677.
Step-by-step explanation:
The amount in the checking account after all the transactions would be $677.
Here's the breakdown of the transactions:
Starting balance: $910
Bill payment: -$185
Withdrawal for lunch: -$30
Purchase of pants: -$43
Purchase of gift card: -$15
Refund for pants: +$43
Total = $910 - $185 - $30 - $43 - $15 + $43 = $677
For the last 20 years, Mr. Bean has weighed 120 pounds,give or take 4 pounds. Write anabsolute value inequality that models this situation.Write a compound inequalityrepresenting all possible weights for Mr. Bean.
Answers
An absolute value inequality that models this situation: \(|x-120|\leq 4\)
The required compound inequality representing all possible weights for Mr. Bean.: \(116\leq x\leq 124\)
Given: For the last 20 years,
Mr. Bean has weighed 120 pounds, give or take 4 pounds.
To write: a) An absolute value inequality that models this situation.
b) a compound inequality representing all possible weights for Mr. Bean.
Computation:
Let x be the actual weight of Mr. Bean,
then
Required absolute inequality:\(|x-120|\leq 4\)
It can be written as
\(-4 \leq x-120\leq 4\)
Add 120 on all sides , we get
\(120-4\leq x\leq120+4\)
\(116\leq x\leq 124\)
The required compound inequality representing all possible weights for Mr. Bean.: \(116\leq x\leq 124\)
Learn more:
https://brainly.com/question/13054155?referrer=searchResults
Help me, please I'd appreciate it
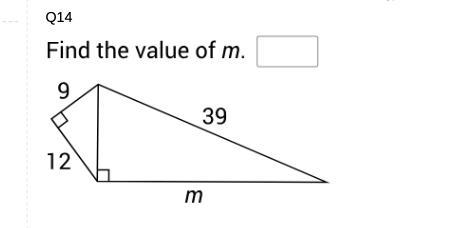
Answers
Answer:
m = 36
Step-by-step explanation:
A^2 + B^2 = C^2
81 + 144 = 225
square root of 225 = 15
n = 15
m = ?
39 = 39
225 + m ^2 = 1521
m^2 = 1296
m = 36.
CHECK :
225 + 1296 = 1521
CORRECT!
show your stepsWhat is the solution of the equation?SEE IMAGE

Answers
Given the equation
\(\begin{gathered} 3\text{ }\sqrt[5]{(x+2)^3\text{ }}\text{ + 3 = 27} \\ \end{gathered}\)Subtract 3 from both sides
\(\begin{gathered} 3\text{ }\sqrt[5]{(x+2)^3\text{ }}\text{ + 3-3 = 27}-3 \\ \\ 3\text{ }\sqrt[5]{(x+2)^3\text{ }}\text{ = }24 \end{gathered}\)Divide both sides by 3
\(\begin{gathered} \text{ }\sqrt[5]{(x+2)^3\text{ }}\text{ = }\frac{24}{3} \\ \text{ }\sqrt[5]{(x+2)^3\text{ }}\text{ = 8} \\ \end{gathered}\)Raise both sides to power 5 to remove the 5th root on the left hand side
\(\begin{gathered} \text{ (}\sqrt[5]{(x+2)^3\text{ }})^5=8^5 \\ \\ (x+2)^3=(8^{})^5 \\ (x+2)^3=\text{ 32768} \\ \end{gathered}\)Take the cube root of both sides
\(\begin{gathered} \sqrt[3]{(x+2)^3}^{}=\sqrt[3]{32768} \\ (x+2\text{ )= 32} \\ \end{gathered}\)Subtract 2 from both sides
x + 2 = 32
x = 32 - 2
x = 30
The solution to the equation is x = 30