32 = q over 2.
I don’t know please help me
Answers
\(32 = \frac{q}{2} \)
First step multiply both sides by 2 to cancel the numerator of q
\(32 \times 2 = \frac{q}{2} \times 2 \\ 64 = q\)
PLEASE MARK BRAINLIEST
32/1 = q/2
you must make both fractions have the same least common denominator. In this case, it’s 2.
32x2= 64
64/2 = q/2
q= 64
Related Questions
I need solution to this question tutor

Answers
Answer:
x=3 and y=
Step-by-step explanation:
Answer:
x=5 and y any number
Step-by-step explanation:
Josie has $ 47 left on her checking account. if she writes for $55, what will Josie' s balance be?
Answers
Answer:
$102
Step-by-step explanation:
Angle theta is in standard position and (-7, 6) is a point on the terminal side of theta.
What is the exact value of csc in simplest form with a rational denominator?
Answers
To find the exact value of the cosecant (csc) of an angle in standard position with a given point on its terminal side, we can use the coordinates of the point to determine the values of the adjacent, opposite, and hypotenuse sides of a right triangle.
In this case, the given point is (-7, 6). To determine the values of the sides, we can use the Pythagorean theorem.
The adjacent side (x-coordinate) is -7.
The opposite side (y-coordinate) is 6.
Using the Pythagorean theorem:
hypotenuse^2 = adjacent^2 + opposite^2
hypotenuse^2 = (-7)^2 + 6^2
hypotenuse^2 = 49 + 36
hypotenuse^2 = 85
Taking the square root of both sides, we get:
hypotenuse = √85
The cosecant (csc) of an angle is the reciprocal of the sine (sin) of that angle. The sine can be determined using the opposite side and the hypotenuse:
sin(theta) = opposite / hypotenuse
sin(theta) = 6 / √85
To find the csc(theta), we take the reciprocal of the sine:
csc(theta) = 1 / sin(theta)
csc(theta) = 1 / (6 / √85)
csc(theta) = √85 / 6
Therefore, the exact value of csc(theta) with a rational denominator is √85 / 6.
Help ASAP please
Suppose that you deposit $6500 into a bank account that pays 4% annual interest compounded continuously. Assuming that you make no other deposits or withdrawals, how long will it take before your account balance reaches $10,000?
Round your answer to the nearest tenth.
Answers
The time it will take for your account balance to reach $10,000 is given as follows:
t = 10.8 years.
What is continuous compounding?The balance of an account after t years, using continuous compounding, is given as follows:
A(t) = A(0)e^(kt).
In which:
A(0) is the initial deposit.k is the interest rate, as a decimal.The parameters for this problem are given as follows:
A(0) = 6500, k = 0.04.
Hence the time needed for a balance of $10,000 is obtained as follows:
10000 = 6500e^(0.04t)
e^(0.04t) = 10000/6500
0.04t = ln(10000/6500) -> ln is the inverse operation of the exponential
t = ln(10000/6500)/0.04
t = 10.8 years.
More can be learned about continuous compounding at https://brainly.com/question/7513822
#SPJ1
The general equation for depreciation is given by y = A(1 – r)t, where y = current value,
A = original cost, r = rate of depreciation, and t = time, in years.
The original value of a car is $24,000. It depreciates 15% annually. What is its value in 4 years?
Answers
Using the general equation for depreciation which is y = A(1 – r)^t, The value of the car in 4 years is $12528.15
How to find the value of the car in 4 yearsThe value of the car is solved by using the formula for depreciation which is y = A(1 – r)t
definition of variables
where
y = current value, = ?
A = original cost, = $24,000
r = rate of depreciation, = 15% and
t = time, in years. = 4 years
substituting the variables
current value, y = A(1 – r)t
current value, y = 24000 * (1 - 0.15)⁴
current value, y = 12528.15
the depreciation is $12528.15
Learn more about depreciation at:
https://brainly.com/question/27971176
#SPJ1
A quality report for a production line shows a score of 59 points on a 65-point inspection test. A passing score is 95% compliance. Did the production line pass inspection?
Answers
Answer:
the production line did not pass
Step-by-step explanation:
Plz help before 12 j

Answers
2. Not equal to
3. Is equal to
4. Not equal to
5. Is equal to
Step-by-step explanation:
1 - 5 is not equal to 8
2 - 16 is not equal to 8
3 - 12 is equal to 12
4 - 5 is not equal to 17
5 - 0 is not equal to 4
What is the area of a triangle with vertices at (−4, −6), (1, −6), and (1, 2)?
Answers
Answer:
20
Step-by-step explanation:
firstly let's find out the side lengths of the triangle using formula
\(length \: = \: \sqrt{(y₂-y1) + ( y₂-y1)}\)
length of AB
\( \sqrt{( - 6 - 2) {}^{2} + ( - 4 - 1) {}^{2} } = \sqrt{89} \)
length of AC
\( \sqrt{( - 6 - 2) {}^{2} + (1 - 1) {}^{2} } = 8\)
length of BC
\( \sqrt{( - 6 - ( - 6)) {}^{2} + (1 - ( - 4)) {}^{2} } = 5\)
Now we have all three side lengths:
a =√89 b = 8 and c = 5
using this formula to find the semi perimeter where a, b and c are the side lengths, input them in
\(s \: = \: \frac{a + b + c}{2} \)
\(s = \frac{ \sqrt{89} + 8 + 5 }{2} = \frac{13 + \sqrt{89} } {2} \)
Use heron's formula
\(area = \sqrt{s(s - a)(s - b)(s - c)} \)
\(area = \sqrt{ \frac{13 + \sqrt{89} }{2}(\frac{13 + \sqrt{89} }{2} - \sqrt{89})( \frac{13 + \sqrt{89} }{2} - 8)(\frac{13 + \sqrt{89} }{2} - 5 } = 20\)
area = 20

Which is the graph of y ≤ 1 – 3x?
Answers
Step-by-step explanation:
To graph an equation using the slope and y-intercept, 1) Write the equation in the form y = mx + b to find the slope m and the y-intercept (0, b). 2) Next, plot the y-intercept. 3) From the y-intercept, move up or down and left or right, depending on whether the slope is positive or negative.

(PLEASE HELP ITS THE LAST QUESTION)
Find the measure of angle L.
A) 21.6°
B) 43.8°
C) 33.4°
D) 21.9°

Answers
Answer:
A
Step-by-step explanation:
lemme meh knw if it was helpful..
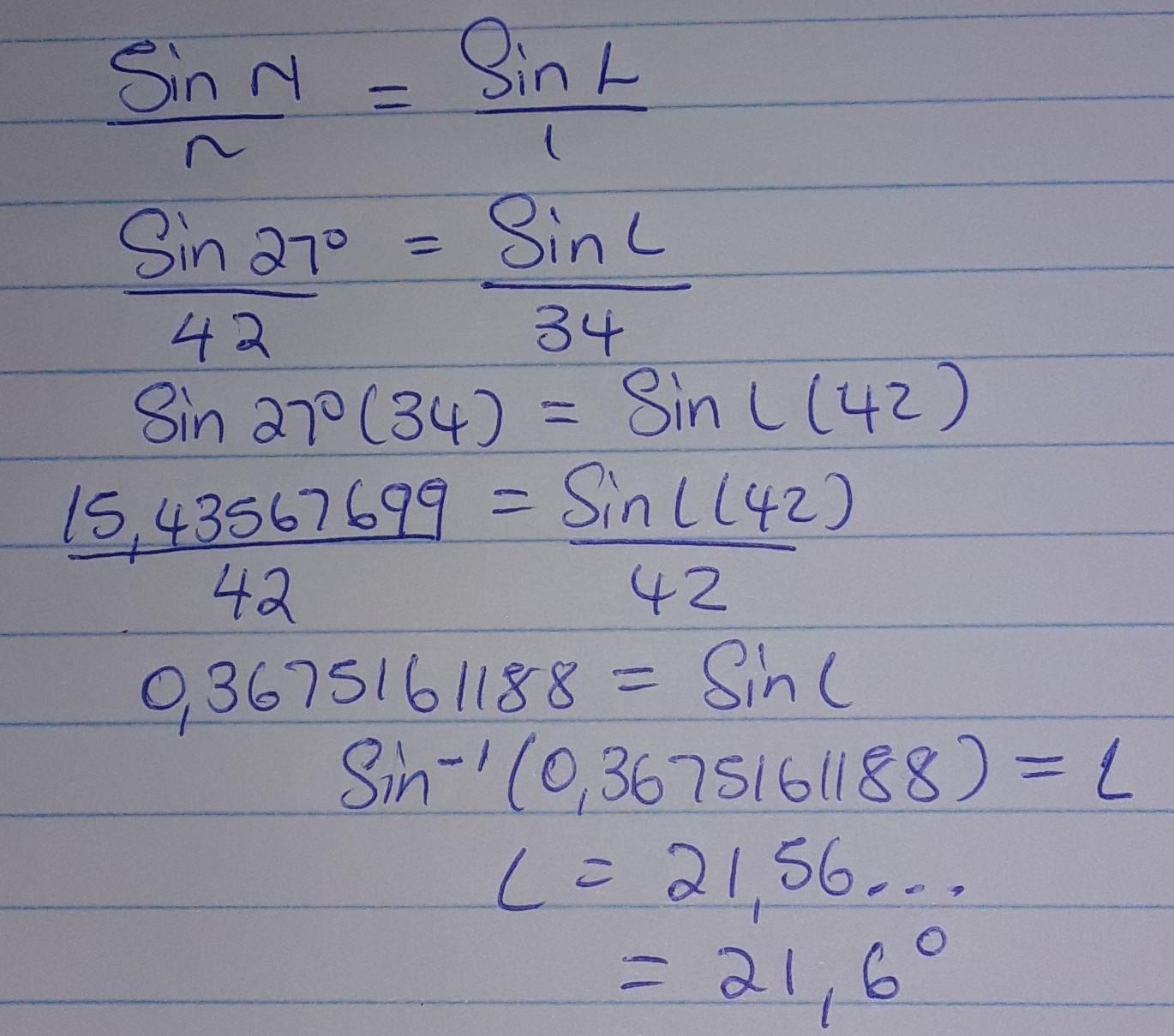
100 Points! Geometry question. Photo attached. Please show as much work as possible. Thank you!

Answers
The proof of ΔRUV ≅ ΔSUT is shown below.
Given that:
RSTV is a rectangle and U is the midpoint of VT.
Here, We have to Prove:
⇒ ΔRUV ≅ ΔSUT
Now, We can prove as;
Statement Reason
1) RSTV is a rectangle Given
2) Angle V and T are Because every angle in a rectangle is 90
right triangle.
3) ∠V ≅ ∠T Because both are right angle.
4) U is the midpoint of VT. Given
5) VU = UT By midpoint theorem.
6) VR ≅ TS Opposite sides of rectangle.
7) ΔRUV ≅ ΔSUT By SAS congruency theorem.
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ1
Last year the depth of the river was 4.2 feet deep.
This year it dropped 21%.
Find the depth of the river this year to cross it.
PLEASE HELP ME
Answers
Use a calculator to graph f(x) = 2x ^ 3 - 6x ^ 2 - 4x + 1 Which are the approximate x-values of the local maximum and local minimum rounded to the nearest tenth?
A) max ≈ -15.6 , min ≈ 1.6
B) max ≈ 1.6 , min ≈ -15.6
C) max ≈ 2.3 , min ≈ -0.3
D) max ≈ -0.3 , min ≈ 2.3
Answers
The approximate x-values for the local maximum and the local minimum are given as follows:
D) max ≈ -0.3 , min ≈ 2.3.
What are the relative minimums and the relative maximums of a function?The relative minimums of a function are given by the points in which the function's behavior changes from decreasing to increasing.The relative maximums of a function, meanwhile, are given by the points in which the function's behavior changes from increasing to decreasing.Hence the critical points of the graphed function are given as follows:
Maximum: x = -0.3.Minimum: x = 2.3.More can be learned about relative minimums of a function at https://brainly.com/question/9839310
#SPJ1

Complete the set of data with value so that the mean of the data is 24?
26, 35, 10, 18, 15, 37, 25, 20, 15, ?
Answers
Answer:
Step-by-step explanation:
Lala
Skskskskdkdkd0222222
25×28 by distributive property
Answers
Answer:
700
Step-by-step explanation:
25 x 28
there is only one property and its multiplication
The area of the triangle formed by the x and y intercepts of the parabola y=0.5(x-3)(x+k) is 1.5 find all possible values of k
Answers
Answer:
The possible values of k are -0.56, -3.56, -2 and -1.
Step-by-step explanation:
We have the equation of the parabola, .
Substituting x=0, we get that i.e. y = -1.5k
So, the y-intercept is (0,-1.5k).
Thus, the height of the triangle becomes |-1.5k| = 1.5k
Again, substituting y=0, i.e. i.e. x=3 and x=-k
So, the x-intercepts are (3,0) and (-k,0).
Thus, the base of the triangle is 3+k if k>-3 or -3-k if k<-3.
We see that 'k' cannot be 0 or -3 as if k=0, then height = 0, which is not possible. If k= -3, then the base = 0, which is also not possible.
As, area of a triangle = .
Substituting the values, we get,
1.5=
i.e.
i.e. k = -0.56 and k = -3.56
or
1.5=
i.e.
i.e. k = -2 and k = -1.
Thus, the possible values of k are -0.56, -3.56, -2 and -1.
y = 1/3x -1
x-intercept (3,0)
How did they get this answer? Somebody please help
Answers
Here's how to do it:
Substitute y with zero:
0 = (1/3)x - 1
Add 1 to both sides:
1 = (1/3)x
Multiply both sides by 3:
3 = x
So the x-intercept of the line y = (1/3)x - 1 is (3,0). This means that the line crosses the x-axis at the point (3,0).
In conclusion, the x-intercept of the line y = (1/3)x - 1 is (3,0), which means that the line crosses the x-axis at the point (3,0).
Answer:
Step-by-step explanation:
x-intercept is where the line cuts the x-axis. That is, when y=0.
Substitute y=0 and we get:
\(0=\frac{1}{3} x-1\)
\(1=\frac{1}{3} x\)
\(x=3\)
So x-intercept is the point (3,0).
Jason planted and staked a tree. The stakes are 21 ft from the base of the tree. They are connected to wires that attach to the trunk at a height of 20 ft. Find the length of a wire.
14 ft
15 ft
20 ft
29 ft
Answers
Based on the height that the wires attach, and the base length of the stakes, the length of the wire is 29 ft.
How long are the wires?This can be solved with the Pythagorean theorem because the height can be treated as the height of a right-angled triangle. The base as the base of the triangle.
The length of the wire is the hypothenuse.
Length:
c² = a² + b²
c² = 21² + 20²
c² = 841
c = √841
= 29 ft
Find out more on the Pythagorean theorem at https://brainly.com/question/343682.
#SPJ1
you want to install molding around the circular room. How much it would cost you to install the molding that you picked if it cost $4.22 per foot?
Answers
The cost of the molding is given as follows:
$119.30.
What is the measure of the circumference of a circle?The circumference of a circle of radius r is given by the equation presented as follows:
C = 2πr.
The parameters for this problem are given as follows:
d = 9 -> r = 4.5.
(as the radius is half the diameter)
Hence the circumference is given as follows:
C = 2 x π x 4.5
C = 28.27 ft.
The cost is of $4.22 per ft, hence the total cost is given as follows:
4.22 x 28.27 = $119.30.
More can be learned about the circumference of a circle at brainly.com/question/12823137
#SPJ1

Just these need to be done appreciate it Number 12

Answers
Explanation:
The coordinates are given below as
\(\begin{gathered} Q(-6,11) \\ R(2,-1) \\ S(-4,8) \\ T(-1,10) \end{gathered}\)Concept:
Rule for perpendicularity,
\(m_1\times m_2=-1\)Rule for parallelism
\(m_1=m_2\)Step 1:
We will calculate the slope of QR using the formula below
\(m_1=\frac{y_2-y_1}{x_2-x_1}\)By substituting the values, we will have
\(\begin{gathered} m_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ m_1=\frac{-1-11}{2-(-6)} \\ m_1=-\frac{12}{2+6} \\ m_1=-\frac{12}{8} \\ m_1=-\frac{3}{2} \end{gathered}\)Step 2:
Calculate the slope of RT using the formula below
\(\begin{gathered} m_2=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ \end{gathered}\)By substituting the values, we will have
\(\begin{gathered} m_2=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\ m_2=\frac{10-8}{-1-(-4)} \\ m_2=\frac{2}{-1+4} \\ m_2=\frac{2}{3} \end{gathered}\)Hence,
\(\begin{gathered} m_1\ne m_2(not\text{ }parllel) \\ m_1\times m_2=-\frac{3}{2}\times\frac{2}{3}=-1 \end{gathered}\)Hence,
The final answer is
\(Perpendicular\)In a dart game, Awasin and Tally each threw the darts 10 times. Tally
had three (+2) scores, three (-3) scores and four (+1) scores. Awasin had
four (+2) scores, four (-3) scores, and two (+1) scores. The winner had the
greater score. Who won the game and what was their score?
Answers
Tally won the dirt throwing game and his score was 1.
What is a numerical expression?A numerical expression is a mathematical statement written in the form of numbers and unknown variables. We can form numerical expressions from statements.
From the given information, The score of Tally is,
= 3×2 - 3×3 + 4×1.
= 6 - 9 + 4.
= 1.
The score of Awasin is,
= 4×2 - 4×3 + 2×1.
= 8 - 12 + 2.
= - 2.
So, Tally won the game and his score is 1.
learn more about numerical expressions here :
https://brainly.com/question/29199574
#SPJ1
I need help!!!!please someone tell me the answer!!!!

Answers
Answer:
c: v=5000(1.35)
Step-by-step explanation:
3.5 interest in point-slope decimal form is 1.35.
v=5000(1.35) is final answer
find the perimeter of the composite figure. 11 19.5 16 m 18m

Answers
The perimeter of the composite figure that is given above would be = 96.6m.
How to calculate the perimeter of the given figure?To calculate the perimeter of the given shape, it has to be divided into two.
First shape is a rectangle. Therefore the perimeter of a rectangle is calculated with the formula = 2(l+w)
Where ;
length = 16m
width = 11m
perimeter = 2(16+11)
= 2×27
= 54m
The second shape:
Perimeter of triangle = l+w+h
where;
length = 18-11 = 7m
width = 16m
height = 19.5m
perimeter = 7+16+19.5 = 42.5m
Therefore, the perimeter of the shape = 54+42.5 = 96.6m
Learn more about perimeter here:
https://brainly.com/question/31619854
#SPJ1
Heeeelp please, Can be zero or not?
with all steps and explanay.

Answers
The value of integral is 3.
Let's evaluate the integral over the positive half of the interval:
∫[0 to π] (cos(x) / √(4 + 3sin(x))) dx
Let u = 4 + 3sin(x), then du = 3cos(x) dx.
Substituting these expressions into the integral, we have:
∫[0 to π] (cos(x) / sqrt(4 + 3sin(x))) dx = ∫[0 to π] (1 / (3√u)) du
Using the power rule of integration, the integral becomes:
∫[0 to π] (1 / (3√u)) du = (2/3) . 2√u ∣[0 to π]
Evaluating the definite integral at the limits of integration:
(2/3)2√u ∣[0 to π] = (2/3) 2(√(4 + 3sin(π)) - √(4 + 3sin(0)))
(2/3) x 2(√(4) - √(4)) = (2/3) x 2(2 - 2) = (2/3) x 2(0) = 0
So, the value of integral is
= 3-0
= 3
Learn more about Definite integral here:
https://brainly.com/question/30760284
#SPJ1
Answer:
\(3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x\approx 0.806\; \sf (3\;d.p.)\)
Step-by-step explanation:
First, compute the indefinite integral:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x\)
To evaluate the indefinite integral, use the method of substitution.
\(\textsf{Let} \;\;u = 4 + 3 \sin x\)
Find du/dx and rewrite it so that dx is on its own:
\(\dfrac{\text{d}u}{\text{d}x}=3 \cos x \implies \text{d}x=\dfrac{1}{3 \cos x}\; \text{d}u\)
Rewrite the original integral in terms of u and du, and evaluate:
\(\begin{aligned}\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\int \dfrac{\cos x}{\sqrt{u}}\cdot \dfrac{1}{3 \cos x}\; \text{d}u\\\\&=\int \dfrac{1}{3\sqrt{u}}\; \text{d}u\\\\&=\int\dfrac{1}{3}u^{-\frac{1}{2}}\; \text{d}u\\\\&=\dfrac{1}{-\frac{1}{2}+1} \cdot \dfrac{1}{3}u^{-\frac{1}{2}+1}+C\\\\&=\dfrac{2}{3}\sqrt{u}+C\end{aligned}\)
Substitute back u = 4 + 3 sin x:
\(= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
Therefore:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
To evaluate the definite integral, we must first determine any intervals within the given interval -π ≤ x ≤ π where the curve lies below the x-axis. This is because when we integrate a function that lies below the x-axis, it will give a negative area value.
Find the x-intercepts by setting the function to zero and solving for x in the given interval -π ≤ x ≤ π.
\(\begin{aligned}\dfrac{\cos x}{\sqrt{4+3\sin x}}&=0\\\\\cos x&=0\\\\x&=\arccos0\\\\\implies x&=-\dfrac{\pi }{2}, \dfrac{\pi }{2}\end{aligned}\)
Therefore, the curve of the function is:
Below the x-axis between -π and -π/2.Above the x-axis between -π/2 and π/2.Below the x-axis between π/2 and π.So to calculate the total area, we need to calculate the positive and negative areas separately and then add them together, remembering that if you integrate a function to find an area that lies below the x-axis, it will give a negative value.
Integrate the function between -π and -π/2.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_1=-\displaystyle \int^{-\frac{\pi}{2}}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=- \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{-\frac{\pi}{2}}_{-\pi}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(-\pi\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (-1)}+\dfrac{2}{3}\sqrt{4+3 (0)}\\\\&=-\dfrac{2}{3}+\dfrac{4}{3}\\\\&=\dfrac{2}{3}\end{aligned}\)
Integrate the function between -π/2 and π/2:
\(\begin{aligned}A_2=\displaystyle \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\frac{\pi}{2}}_{-\frac{\pi}{2}}\\\\&=\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}\\\\&=\dfrac{2}{3}\sqrt{4+3 (1)}-\dfrac{2}{3}\sqrt{4+3 (-1)}\\\\&=\dfrac{2\sqrt{7}}{3}-\dfrac{2}{3}\\\\&=\dfrac{2\sqrt{7}-2}{3}\end{aligned}\)
Integrate the function between π/2 and π.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_3=-\displaystyle \int^{\pi}_{\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= -\left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\pi}_{\frac{\pi}{2}}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(\pi\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (0)}+\dfrac{2}{3}\sqrt{4+3 (1)}\\\\&=-\dfrac{4}{3}+\dfrac{2\sqrt{7}}{3}\\\\&=\dfrac{2\sqrt{7}-4}{3}\end{aligned}\)
To evaluate the definite integral, sum A₁, A₂ and A₃:
\(\begin{aligned}\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\dfrac{2}{3}+\dfrac{2\sqrt{7}-2}{3}+\dfrac{2\sqrt{7}-4}{3}\\\\&=\dfrac{2+2\sqrt{7}-2+2\sqrt{7}-4}{3}\\\\&=\dfrac{4\sqrt{7}-4}{3}\\\\ &\approx2.194\; \sf (3\;d.p.)\end{aligned}\)
Now we have evaluated the definite integral, we can subtract it from 3 to evaluate the given expression:
\(\begin{aligned}3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x&=3-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9}{3}-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9-(4\sqrt{7}-4)}{3}\\\\&=\dfrac{13-4\sqrt{7}}{3}\\\\&\approx 0.806\; \sf (3\;d.p.)\end{aligned}\)
Therefore, the given expression cannot be zero.

HELP WITH C
5mph buffer what is the new function and graph?

Answers
The function for fine at every speed should be doubled in construction zones is f(n)= -8.75n+637.5.
What is the function?Functions are the fundamental part of the calculus in mathematics. The functions are the special types of relations. A function in math is visualized as a rule, which gives a unique output for every input x.
The coordinate points from the graph are (10, 550) and (30, 200).
Here, slope = (200-550)(30-10)
= -350/20
= -35/2
= -17.5
Substitute m= -17.5 and (x, y)=(10, 550) in y=mx+c, we get
550=-17.5(10)+c
c=550+175
c=725
So, the equation is y= -17.5x+725
Thus, f(n)= -17.5n+725
a) The fine at every speed should go up by $10.
So, the coordinates are (10, 560) and (30, 210)
New slope (m)= (210-560)(30-10)
= -350/20
= -35/2
= -17.5
Substitute m= -17.5 and (x, y)=(10, 560) in y=mx+c, we get
560=-17.5(10)+c
c=550+175
c=735
So, the equation is y= -17.5x+735
Thus, f(n)= -17.5n+735
b) The fine at every speed should be doubled in construction zones.
So, the coordinates are (20, 550) and (60, 200)
New slope (m)= (200-550)(60-20)
= -350/40
= -8.75
Substitute m= -8.75 and (x, y)=(20, 550) in y=mx+c, we get
550=-8.75(10)+c
c=550+87.5
c=637.5
So, the equation is y= -8.75x+637.5
Thus, f(n)= -8.75n+637.5
Therefore, the function for fine at every speed should be doubled in construction zones is f(n)= -8.75n+637.5.
To learn more about the function visit:
https://brainly.com/question/28303908.
#SPJ1

Simplify the rate:
46 cans of Soda / 8 people
Only enter the numeric amount:
Answers
Answer: 23 cans of soda/4 people.
or (23/4) cans of soda per person.
Step-by-step explanation:
So we have the rate:
46 cans of soda/ 8 people
First, 46 and 8 are multiples of 2, so we can divide both numerator and denominator by 2:
46/2 = 23
8/2 = 4
Then the rate can be:
23 cans of soda/4 people.
Now 23 is a prime number, so we can not simplify it furthermore
Carl earned grades of 62, 78, 59, and 89 on four math tests.
What is the mean of his grades?
A. 68.5
B. 70
C. 72
D. 74
E. 75.5
Answers
Answer:
Mean, m = 72
Step-by-step explanation:
It is given that, Carl earned grades of 62, 78, 59, and 89 on four math tests.
It is required to find the mean of his grades.
Mean of a data is given by :
\(m=\dfrac{\text{sum of observations}}{\text{total no of observations}}\)
Sum of observations is 62 + 78 + 59 + 89 = 288
Total no of observations are 4
So, mean of his grades is :
\(m=\dfrac{288}{4}\\\\m=72\)
So, the mean of his grades is 72.
Option C is correct. If Carl earned grades of 62, 78, 59, and 89 on four math tests, the mean of his grades is 72
Mean is the average of the given data. It is expressed mathematically as:
\(\overlibe x=\frac{\sum x}{N}\)
\(\sum x\) is the sum of the variables
N is the total test taken
\(\sum x = 62 + 78 + 59 + 89\\\sum x = 288\\\\N = 4\)
Substitute the resulting values into the mean formula:
\(\overline x = \frac{288}{4}\\ \overline x =72\)
This shows that the mean of his grades is 72
Learn more here:https://brainly.in/question/2401311
HELPPP!!!
Create a residual plot for your data.

Answers
A residual plot is a scatterplot in which the residuals (vertical distances between the predicted and actual values) are plotted against the independent variable. A residual is defined as the difference between the predicted value (based on the regression equation) and the actual value.
Residual plots are a valuable tool for checking the adequacy of the model. It helps us check whether the assumptions of linearity, independence, equal variance, and normality are met or not.
The most basic way to create a residual plot is to plot the residuals against the fitted values. If the points in the residual plot are randomly scattered around the horizontal axis, then the assumption of linearity has been met.
If the points show a pattern, such as a curved line, then the assumption of linearity has been violated.To create a residual plot, follow these steps:
Step 1: Estimate the regression equation and obtain the predicted values (ŷ) and residuals (e). ŷ = b0 + b1X
Step 2: Plot the residuals on the vertical axis and the independent variable (X) on the horizontal axis
.Step 3: Look for patterns in the residual plot. If the points are randomly scattered around the horizontal axis, then the assumptions of linearity, independence, equal variance, and normality are met. If there is a pattern, such as a curved line, then the assumptions have been violated. A residual plot can be used to detect outliers, influential observations, and nonlinearity.
For such more question on variable
https://brainly.com/question/28248724
#SPJ8
g An irate student complained that the cost of textbooks was too high. He randomly surveyed 36 other students and found that the mean amount of money spent for textbooks was $121.60. If the standard deviation of the population was $6.36, find the 90% confidence interval of the true mean.
Answers
Answer:
A 90% confidence interval of the true mean is [$119.86, $123.34].
Step-by-step explanation:
We are given that an irate student complained that the cost of textbooks was too high. He randomly surveyed 36 other students and found that the mean amount of money spent on textbooks was $121.60.
Also, the standard deviation of the population was $6.36.
Firstly, the pivotal quantity for finding the confidence interval for the population mean is given by;
P.Q. = \(\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }\) ~ N(0,1)
where, \(\bar X\) = sample mean amount of money spent on textbooks = $121.60
\(\sigma\) = population standard deviation = $6.36
n = sample of students = 36
\(\mu\) = population mean
Here for constructing a 90% confidence interval we have used One-sample z-test statistics as we know about population standard deviation.
So, 95% confidence interval for the population mean, \(\mu\) is ;
P(-1.645 < N(0,1) < 1.645) = 0.90 {As the critical value of z at 5% level
of significance are -1.645 & 1.645}
P(-1.645 < \(\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }\) < 1.645) = 0.90
P( \(-1.645 \times {\frac{\sigma}{\sqrt{n} } }\) < \({\bar X-\mu}\) < \(1.645 \times {\frac{\sigma}{\sqrt{n} } }\) ) = 0.90
P( \(\bar X-1.645 \times {\frac{\sigma}{\sqrt{n} } }\) < \(\mu\) < \(\bar X+1.645 \times {\frac{\sigma}{\sqrt{n} } }\) ) = 0.90
90% confidence interval for \(\mu\) = [ \(\bar X-1.645 \times {\frac{\sigma}{\sqrt{n} } }\) , \(\bar X+1.645 \times {\frac{\sigma}{\sqrt{n} } }\) ]
= [ \(121.60-1.645 \times {\frac{6.36}{\sqrt{36} } }\) , \(121.60+1.645 \times {\frac{6.36}{\sqrt{36} } }\) ]
= [$119.86, $123.34]
Therefore, a 90% confidence interval of the true mean is [$119.86, $123.34].
The area of a trapezoid is 48 square centimeters. The height is 6 centimeters and one base 3 times the length of the other base. What are the lengths of the bases?
Answers
The lengths of the bases are: 4cm and 12cm.
Area of a TrapezoidSince the area of a trapezoid is given by the formula;
A = 1/2 (a + b) h.Where a and b are the lengths of the bases and h is the height of the trapezoid.
Hence, in this case scenario; it follows that;
48 = 1/2(x + 3x) 648 = 12xx = 48/12a = x = 4cm
b = 3x = 12cm.
Read more on trapezoid;
https://brainly.com/question/1463152