3. "the product of a number and 5.”
Answers
Answer:
x * 5
Step-by-step explanation:
prosucts refer to multiplication
Related Questions
17. Which quotient will be larger? Explain
how you can tell without dividing.
3,444 : 42
4,368 : 42
Answers
Answer:
4,368 / 42
Step-by-step explanation:
I can tell without answering the problems because if you have a larger amount to divide by, it would lead to people having a higher amount. Meanwhile having a smaller amount to divide by.
elizas backpack weights 18 7/8 pounds with her math book in it. without her math book, her backpack weighs 14 7/9 pounds
Answers
I'm assuming your trying to find the weight of the math book so here it is:
Answer:
4 5/36
Step-by-step explanation:
You'd have to do 18 7/8 - 14 7/9 but you can't subtract them yet because they don't have common denominators. So, you have to multiply the 7/8 by 9 and the 7/9 by 8. Then you would get 63/72 and 56/72. Then you put that into the equation and get, 18 63/72 - 14 53/72. If you subtract those, you get the answer, 4 10/72. Which can be simplified as 4 5/36.
The average price of a certain model of pickup truck in 1991 was $19,500. In 2012, the average price of the pickup truck was $35,100. What is the percentage increase in the average price of the pickup truck?
Answers
The average price of the pickup truck increased by 80%.
To find the percentage increase in the average price of the pickup truck, we need to calculate the difference between the 2012 and 1991 prices, divide that difference by the 1991 price, and then multiply by 100 to get the percentage increase.
First, we need to find the difference between the two prices:
$35,100 - $19,500 = $15,600
Next, we divide the difference by the 1991 price:
$15,600 / $19,500 = 0.8
Finally, we multiply by 100 to get the percentage increase:
0.8 x 100 = 80%
Therefore, the average price of the pickup truck increased by 80%.
for such more question on average price
https://brainly.com/question/25799822
#SPJ11
Solve triangle DEF using the diagram and the given measurements.

Answers
Based on triangle DEF, the missing side lengths include the following:
10. d = 5.1423 units, e = 6.1284 units.
11. e = 17.2516 units, f = 21.6013 units.
12. d = 24.7365 units, f = 26.8727 units.
How to calculate the missing side lengths?In order to determine the missing side lengths, we would apply cosine ratio because the given side lengths represent the adjacent side and hypotenuse of a right-angled triangle.
cos(θ) = Adj/Hyp
Where:
Adj represents the adjacent side of a right-angled triangle.Hyp represents the hypotenuse of a right-angled triangle.θ represents the angle.Part 10.
By substituting the given side lengths cosine ratio formula, we have the following;
cos(40) = e/8
e = 8cos40
e = 6.1284 units.
d² = f² - e²
d² = 8² - 6.1284²
d = 5.1423 units.
Part 11.
E = 53°, d = 13.
cos(53) = 13/f
f = 13/cos(53)
f = 21.6013 units.
e² = f² - d²
e² = 21.6013² - 13²
e = 17.2516 units.
Part 12.
D = 67°, E = 10.5.
cos(67) = 10.5/f
f = 10.5/cos(67)
f = 26.8727 units.
d² = f² - e²
d² = 26.8727² - 10.5²
d = 24.7365 units.
Read more on right-angled triangle here: brainly.com/question/2223099
#SPJ1
Find the perimeter of the pentagon MNPQR with vertices M(2, 4), N(5, 8), P(8, 4), Q(8, 1), and R(2, 1)
Answers
Answer:
The pentagon MNPQR has a perimeter of 22 units.
Step-by-step explanation:
Geometrically speaking, the perimeter of the pentagon is the sum of the lengths of each side, that is:
\(p = MN + NP + PQ + QR + RM\) (1)
\(p = \sqrt{\overrightarrow{MN}\,\bullet \, \overrightarrow{MN}} + \sqrt{\overrightarrow{NP}\,\bullet \, \overrightarrow{NP}} + \sqrt{\overrightarrow{PQ}\,\bullet \, \overrightarrow{PQ}} + \sqrt{\overrightarrow{QR}\,\bullet \, \overrightarrow{QR}} + \sqrt{\overrightarrow{RM}\,\bullet \, \overrightarrow{RM}}\) (1b)
If we know that \(M(x,y) = (2,4)\), \(N(x,y) = (5,8)\), \(P(x,y) = (8,4)\), \(Q(x,y) = (8,1)\) and \(R(x,y) = (2,1)\), then the perimeter of the pentagon MNPQR is:
\(p =\sqrt{(5-2)^{2}+(8-4)^{2}} + \sqrt{(8-5)^{2}+(4-8)^{2}}+\sqrt{(8-8)^{2}+(1-4)^{2}}+\sqrt{(2-8)^{2}+(1-1)^{2}}+\sqrt{(2-2)^{2}+(4-1)^{2}}\)\(p = \sqrt{3^{2}+4^{2}} + \sqrt{3^{2}+(-4)^{2}}+\sqrt{0^{2}+(-3)^{2}}+\sqrt{(-6)^{2}+0^{2}}+\sqrt{0^{2}+3^{2}}\)
\(p = 22\)
The pentagon MNPQR has a perimeter of 22 units.
The pentagon MNPQR has a perimeter of 22 units.
Geometrically speaking, the perimeter of the pentagon is the sum of the lengths of each side, that is:
p = MN + NP + PQ + QR + RMp=MN+NP+PQ+QR+RM (1)
p = \sqrt{\overrightarrow{MN}\,\bullet \, \overrightarrow{MN}} + \sqrt{\overrightarrow{NP}\,\bullet \, \overrightarrow{NP}} + \sqrt{\overrightarrow{PQ}\,\bullet \, \overrightarrow{PQ}} + \sqrt{\overrightarrow{QR}\,\bullet \, \overrightarrow{QR}} + \sqrt{\overrightarrow{RM}\,\bullet \, \overrightarrow{RM}}p=
MN
∙
MN
+
NP
∙
NP
+
PQ
∙
PQ
+
QR
∙
QR
+
RM
∙
RM
(1b)
If we know that M(x,y) = (2,4)M(x,y)=(2,4) , N(x,y) = (5,8)N(x,y)=(5,8) , P(x,y) = (8,4)P(x,y)=(8,4) , Q(x,y) = (8,1)Q(x,y)=(8,1) and R(x,y) = (2,1)R(x,y)=(2,1) , then the perimeter of the pentagon MNPQR is:
p =\sqrt{(5-2)^{2}+(8-4)^{2}} + \sqrt{(8-5)^{2}+(4-8)^{2}}+\sqrt{(8-8)^{2}+(1-4)^{2}}+\sqrt{(2-8)^{2}+(1-1)^{2}}+\sqrt{(2-2)^{2}+(4-1)^{2}}p=
(5−2)
2
+(8−4)
2
+
(8−5)
2
+(4−8)
2
+
(8−8)
2
+(1−4)
2
+
(2−8)
2
+(1−1)
2
+
(2−2)
2
+(4−1)
2
p = \sqrt{3^{2}+4^{2}} + \sqrt{3^{2}+(-4)^{2}}+\sqrt{0^{2}+(-3)^{2}}+\sqrt{(-6)^{2}+0^{2}}+\sqrt{0^{2}+3^{2}}p=
3
2
+4
2
+
3
2
+(−4)
2
+
0
2
+(−3)
2
+
(−6)
2
+0
2
+
0
2
+3
2
p = 22p=22
The pentagon MNPQR has a perimeter of 22 units.
a) Calculate the size of angle x in the diagram
below.
b) Work out the bearing of A from B.

Answers
The angle x in the diagram is 98 degrees.
How to find the angles in parallel lines?When parallel lines are cut by a transversal line, angle relationships are formed such as corresponding angles, alternate interior angle, alternate exterior angles, vertically opposite angles, same side interior angles etc.
Therefore, let's find the angle of x using the angle relationships as follows:
The size of the angle x can be found as follows:
82 + x = 180(same side interior angles)
Same side interior angles are supplementary.
Hence,
82 + x = 180
x = 180 - 82
x = 98 degrees
learn more on angles here: brainly.com/question/24195209
#SPJ1
Mr. Hasson has a coupon that says 25% off. He buys a pair of biking shorts that originally costs $34. He calculates 25% of 34 and determines he needs to pay $8.50 for the shorts
Explain
What is the error?
Why do you think he made that error?
What is the correct way to find the sale price?
Answers

the width of a rectangle is half the length g. write and simplify an expression that represents the perimeter and area of the rectangle
Answers
The perimeter 2a+g unit and area a*g/2 unit² of the rectangle.
What is a rectangle?
Rectangles are quadrilaterals having four right angles in the Euclidean plane of geometry. Various definitions include an equiangular quadrilateral,
The area of rectangle is A = a*b
here given is b = g/2unit
The area will be a*g/2 unit²
The perimeter of the rectangle is 2(a+b)
perimeter will be 2(a+g/2) = 2a+g unit
hence the perimeter and area of the rectangle are a*g/2 unit² and 2a+g unit respectively.
Learn more about rectangular by following the link below.
https://brainly.com/question/25292087
#SPJ1
Which expression represents a negative number?
A. -4/5(-8/9)
B. 4/5*8/9
C. -4/5*8/9
D. -9/8*(-3/4)
Answers
Its C.
Negative x Negative is positive, so its not A or D.
Positive x Positive is Positive, so its not B either.
C is your option because Positive x Negative is Negative, and vice verca.
Answer:
C
Step-by-step explanation:
this is because a negative number multiplied with a negative number gives you a positive, a positive number multiplied with a positive number gives you a positive but a negative number multiplied with a positive gives you a negative so the answer is C.
for more information watch videos about the rules of positive and negative numbers.
Use technology to find points and then graph the function y=-2\log_2(x+3)+2,y=−2log 2 (x+3)+2, following the instructions below.
Answers

The graph of the given function is attached below.
What is the function?A relationship between a group of inputs and one output is referred to as a function. In plain English, a function is an association between inputs in which each input is connected to precisely one output. A domain, codomain, or range exists for every function. Typically, f(x), where x is the input, is used to represent a function.
The graph of the function y = -2log2(x+3) + 2 is a downward-sloping curve that approaches the x-axis as x approaches infinity.
The curve is defined only for positive values of x, as the logarithm is undefined for negative values.
As x increases, the logarithm term inside the parentheses becomes larger in magnitude, causing the value of y to decrease rapidly.
The curve approaches the x-axis but never touches it, as the logarithm term will never reach zero.
Learn more about function here:
https://brainly.com/question/29633660
#SPJ2

Find the value of x.

Answers
Answer:
x=18
Step-by-step explanation:
see answer
Suppose x, y and z are integers. Prove that, if 3x−y + 5z is even, then at least one of x, y or z is even.
Answers
Given:
x, y and z are integers.
To prove:
If \(3x-y+5z\) is even, then at least one of x, y or z is even.
Solution:
We know that,
Product of two odd integers is always odd. ...(i)
Difference of two odd integers is always even. ...(ii)
Sum of an even integer and an odd integer is odd. ...(iii)
Let as assume x, y and z all are odd, then \(3x-y+5z\) is even.
\(3x\) is always odd. [Using (i)]
\(5z\) is always odd. [Using (i)]
\(3x-y\) is always even. [Using (ii)]
\((3x-y)+5z\) is always odd. [Using (iii)]
\(3x-y+5z\) is always odd.
So, out assumption is incorrect.
Thus, at least one of x, y or z is even.
Hence proved.
Please I need step by step solution.
Q/ sin135° Use half angle identity.
Answers
Answer:
Step-by-step explanation:
Sin (90 + Ф ) =Cos Ф
135° = 90 + 45
Sin 135° = Sin (90 + 45)
= Cos 45°
\(= \dfrac{1}{\sqrt{2}}\)
fully factorise: x³+3x²-6x-8
Answers

Answer:
(x-2) (x+1) (x+4)
Step-by-step explanation:
x^3+3x^2-6x-8
Rearranging the terms,
(x^3 - 8) + (3x^2 - 6x)
a^3 - b^3 = (a-b) (a^2 + ab + b^2)
(x^3 - 8) = (x^3 - 2^3) = (x-2) (x^2 + 2x + 4)
(3x^2 - 6x) = 3x(x-2)
So, x^3 + 3x^2 -6x -8
= (x-2) (x^2 + 2x +4) + 3x(x-2)
(x-2) is the common factor,
= (x-2) ( x^2 +2x+4 + 3x)
= (x-2) (x^2 + 5x + 4)
= (x-2) (x^2 + 4x + x + 4)
= (x-2) (x(x+4) +1(x+4))
= (x-2) (x+1) (x+4)
find the rational form of 71.625
Answers
Answer:
71 5/8Step-by-step explanation:
A rational number is a nonrepeating fraction. To convert, we need to put 71,625 over 1000.
We divide 1000 by 125.
This simplifies to 573/8.
Then we get the whole number part of the mixed number.
71 5/8___________________________________________________I AM ALWAYS HAPPY TO HELP :)Last summer we went camping in Yosemite, and the first night we did a bad thing: we left out food on the ground. A bear came along and ripped up one-third of our total number of dried meals. The next day we ate four of the remaining meals and tied the food up in a tree. It didn’t seem to help because one-third of the meals we had left were ripped open by another bear. During our third day, we ate four more meals and that night, despite everything we did, one-half of our remaining dried meals were ripped apart. We gave up, ate the four remaining dried meals, and headed home. Can you tell how many dried meals we started with?
Answers
Answer: We started with 36 dried meals
Step-by-step explanation: Let x be the number of dried meals we started with. After the first night, we had x - x/3 = 2x/3 meals left. After the second day, we had 2x/3 - 4 meals left. After the second night, we had (2x/3 - 4) - (2x/3 - 4)/3 = 4x/9 - 8/3 meals left. After the third day, we had (4x/9 - 8/3) - 4 meals left. After the third night, we had ((4x/9 - 8/3) - 4)/2 meals left. This was equal to 4, so we can set up an equation and solve for x:
((4x/9 - 8/3) - 4)/2 = 4
Multiplying both sides by 2, we get:
(4x/9 - 8/3) - 4 = 8
Adding 4 to both sides, we get:
4x/9 - 8/3 = 12
Multiplying both sides by 9, we get:
4x - 24 = 108
Adding 24 to both sides, we get:
4x = 132
Dividing both sides by 4, we get:
x = 33
However, if x = 33, then the number of dried meals we had left after the third night would be ((4*33/9 - 8/3) - 4)/2 = 4.666… This is not a whole number, so it means that we either had more or less than 4 meals left. Since we ate the four remaining meals and headed home, we know that we had exactly 4 meals left. Therefore, x cannot be 33. The closest integer to 33 that satisfies the equation is 36.
Hope this helps, and have a great day! =)
Answer:
33 meals
Step-by-step explanation:
You want to know the number of meals you started with if 4 were left after half those at the end of the third day were destroyed, 4 were eaten on the third day after 1/3 those at the end of the second day were destroyed, 4 were eaten on the second day after 1/3 of the starting number were destroyed.
ScenarioAssume we started with x meals. The sequence of events seems to be ...
1/3 were destroyed overnight, so 2/3x remained
4 were eaten next day, so (2/3x -4) remained
1/3 were destroyed overnight, so 2/3(2/3x -4) remained
4 were eaten on the third day, so 2/3(2/3x -4) -4 remained
1/2 were destroyed, so 1/2(2/3(2/3x -4) -4) remained
The number remaining was 4.
SolutionUndoing the layers of the expression, we have ...
1/2(2/3(2/3x -4) -4) = 4
2/3(2/3x -4) -4 = 8 . . . . . . . multiply by 2
2/3(2/3x -4) = 12 . . . . . . . . . add 4
2/3x -4 = 18 . . . . . . . . . . . . . multiply by 3/2
2/3x = 22 . . . . . . . . . . . . . . . add 4
x = 33 . . . . . . . . . . . . . . . . . . multiply by 3/2
You started with 33 meals.
<95141404393>
Please help me with this

Answers
Answer:
c = 13
Step-by-step explanation:

Answer: the answer would be 169
Step-by-step explanation:
\(5x^{2} +12x^{2} = 169\)
what is the slope- intercept form of 3x-y=8
Answers
Answer:
\(y=3x-8\)
Step-by-step explanation:
slope intercept form is \(y=mx+b\) so just get the equation to look like this\(3x-y=8\\3x-(3x)-y=8-(3x)\\-y=-3x+8\\y=3x-8\)Write an expression for the following situation
The sum of -7 and a number 15 units to the right of 0
Answers
Answer:
15 + -7 OR 15 - 7
Step-by-step explanation:
A hovercraft takes off from a platform. Its height (in meters), x xx seconds after takeoff, is modeled by h ( x ) = − ( x − 11 ) ( x + 3 ) h(x)=−(x−11)(x+3)h, left parenthesis, x, right parenthesis, equals, minus, left parenthesis, x, minus, 11, right parenthesis, left parenthesis, x, plus, 3, right parenthesis What is the height of the hovercraft at the time of takeoff?
Answers
Answer:
3²/₃ m
Step-by-step explanation:
Since h(x)= −(x−11)(x+3) represents the height of the hovercraft after x seconds, at the time of takeoff, x = 0.
So, the height at takeoff is h(0) = −(0 − 11)(0 + 3)
= -(-11)/3
= 11/3 m
= 3²/₃ m
Answer: 33 seconds
Step-by-step explanation: Khan Academy
i need help! what is the y-intercept of the line 2x + 3y = 6?
Answers
Answer:
The y-intercept of this line is 2.
Step-by-step explanation:
To find where this line reaches the y axis, you simply need to assign the value 0 to x, and solve for y:
\(2x + 3y = 6\\2(0) + 3y = 6\\3y = 6\\y = 6/3\\y = 2\)
So the y intercept of that line is 2
If the scale factor between the sides is 5, what are the scale factors between the surface areas and volumes?
Answers
If the scale factor between the sides is 5, the scale factor between the surface areas will be 25, and the scale factor between the volumes will be 125.
When the scale factor between the sides of a shape is given, the scale factors between the surface areas and volumes can be determined by considering the relationship between the dimensions.
Let's denote the scale factor between the sides as "k."
For surface area:
The surface area of a shape is determined by the square of its linear dimensions. Therefore, the scale factor for the surface area will be k^2. In this case, if the scale factor between the sides is 5, the scale factor between the surface areas will be 5^2 = 25.
For volume:
The volume of a shape is determined by the cube of its linear dimensions. Hence, the scale factor for the volume will be k^3. Given that the scale factor between the sides is 5, the scale factor between the volumes will be 5^3 = 125.
Therefore, if the scale factor between the sides is 5, the scale factor between the surface areas will be 25, and the scale factor between the volumes will be 125.
For more questions on scale factor
https://brainly.com/question/29576241
#SPJ8
Which function represents exponential decay?
A. f(x) = 0.25(1.06)
B. f(x) = 18 +0.9x
c. f(x) = 412 + 1.03x
D. f(x) = 268(0.86)*
Answers
Answer: The function that represents exponential decay is:
D. f(x) = 268(0.86)^x
This function has a base of 0.86, which is less than 1. As x increases, the value of the function decreases exponentially. This is the characteristic of exponential decay, where the value of a quantity decreases at a constant percentage rate over time.
Option A, f(x) = 0.25(1.06), represents exponential growth, as the base (1.06) is greater than 1.
Option B, f(x) = 18 + 0.9x, represents linear growth, as the value of the function increases linearly with x.
Option C, f(x) = 412 + 1.03x, also represents linear growth, as the value of the function increases linearly with x.
Step-by-step explanation:
Diana is painting statues. She has 7/8 of a liter of paint remaining. Each statue requires 1/20 of a liter of paint. How many statues can she paint?
Answers
Answer:
She can paint 17 statues
Step-by-step explanation:
Sorry I don’t really know how to show my work
Answer:
140/8
simplified: 35/2
decimal: 17.5
Step-by-step explanation:
honestly, I don't know how to show my work but I hope this helps.

Kerri has a germen shepherd that has a mass of 30,000 grams. how many kilograms is 30,000 grams
Answers
explanation: Each 1000 grams converts to 1 kilogram
Explain how the tangents of complementary angles are related.
Answers
Answer:
tan(α) = 1/tan(90°-α)
Step-by-step explanation:
The tangent of one is the reciprocal of the tangent of the other.
__
In a right triangle, ...
tan = opposite/adjacent
For the two complementary acute angles in such a triangle, opposite and adjacent are swapped. That is the tangent of one is the inverse of the tangent of the other. (That inverse is also known as the cotangent.)
tan(α) = cot(90°-α) = 1/tan(90°-α)
a rectangular solid (with a square base) has a surface area of 433.5 square centimeters. find the dimensions that will result in a solid with maximum volume.
Answers
The dimensions that will result in a solid with maximum volume are approximately x = 12.02 centimeters and h = 5.01 centimeters.
Let the side of the square base be x, and let the height of the rectangular solid be h. Then, the surface area of the solid is given by:
Surface area = area of base + area of front + area of back + area of left + area of right
Surface area = x² + 2xh + 2xh + 2xh + 2xh = x² + 8xh
We are given that the surface area is 433.5 square centimeters, so we can write: x² + 8xh = 433.5
We want to find the dimensions that will result in a solid with maximum volume. The volume of the solid is given by:
Volume = area of base × height = x² × h
We can use the surface area equation to solve for h in terms of x:
x² + 8xh = 433.5
h = (433.5 - x²)/(8x)
Substituting this expression for h into the volume equation, we get:
Volume = x² × (433.5 - x²)/(8x) = (433.5x - x³)/8
To find the maximum volume, we need to find the value of x that maximizes this expression. To do this, we can take the derivative of the expression with respect to x, set it equal to zero, and solve for x:
d(Volume)/dx = (433.5 - 3x²)/8 = 0
433.5 - 3x² = 0
x² = 144.5
x = sqrt(144.5) ≈ 12.02
We can check that this is a maximum by computing the second derivative of the volume expression with respect to x:
d²(Volume)/dx² = -3x/4
At x = sqrt(144.5), this is negative, which means that the volume is maximized at x = sqrt(144.5).
Substituting x = sqrt(144.5) into the expression for h, we get:
h = (433.5 - (sqrt(144.5))²)/(8×sqrt(144.5))
h = 433.5/(8×sqrt(144.5)) - sqrt(144.5)/8
h = 5.01
Learn more about volume here:
https://brainly.com/question/6286323
#SPJ11
The dimensions of the rectangular solid that will result in a maximum volume are approximately.\(6.34 cm \times 9.03 cm \times 9.03 cm.\)
Let's assume that the length, width, and height of the rectangular solid are all equal to x, so the base of the solid is a square.
The surface area of the rectangular solid can be expressed as:
\(SA = 2xy + 2xz + 2yz\)
Substituting x for y and z, we get:
\(SA = 2x^2 + 4xy\)
We are given that the surface area is 433.5 square centimeters, so:
\(2x^2 + 4xy = 433.5\)
Simplifying, we get:
\(x^2 + 2xy - 216.75 = 0\)
Using the quadratic formula to solve for y, we get:
\(y = (-2x\± \sqrt (4x^2 + 4(216.75)))/2\)
\(y = -x \± \sqrt (x^2 + 216.75)\)
Since the base of the rectangular solid is a square, we know that y = z. So:
\(z = -x \± \sqrt(x^2 + 216.75)\)
The volume of the rectangular solid is given by:
\(V = x^2y\)
Substituting y for\(-x + \sqrt (x^2 + 216.75),\) we get:
\(V = x^2(-x + \sqrt(x^2 + 216.75))\)
Expanding and simplifying, we get:
\(V = -x^3 + x^2\sqrt(x^2 + 216.75)\)
The dimensions that will result in a solid with maximum volume, we need to find the value of x that maximizes the volume V.
We can do this by taking the derivative of V with respect to x, setting it equal to zero, and solving for x:
\(dV/dx = -3x^2 + 2x\sqrt(x^2 + 216.75) + x^2/(2\sqrt (x^2 + 216.75)) = 0\)
Multiplying both sides by \(2\sqrt (x^2 + 216.75)\) to eliminate the denominator, we get:
\(-6x^2\sqrt (x^2 + 216.75) + 4x(x^2 + 216.75) + x^3 = 0\)
Simplifying, we get:
\(x^3 - 6x^2\sqrt (x^2 + 216.75) + 4x(x^2 + 216.75) = 0\)
We can solve this equation numerically using a graphing calculator or computer software.
\(The solution is approximately x = 6.34 centimeters.\)
Substituting x = 6.34 into the expression for y and z, we get:
\(y = z \approx 9.03 centimeters\)
For similar questions on rectangular
https://brainly.com/question/19819849
#SPJ11
Help me in really struggling
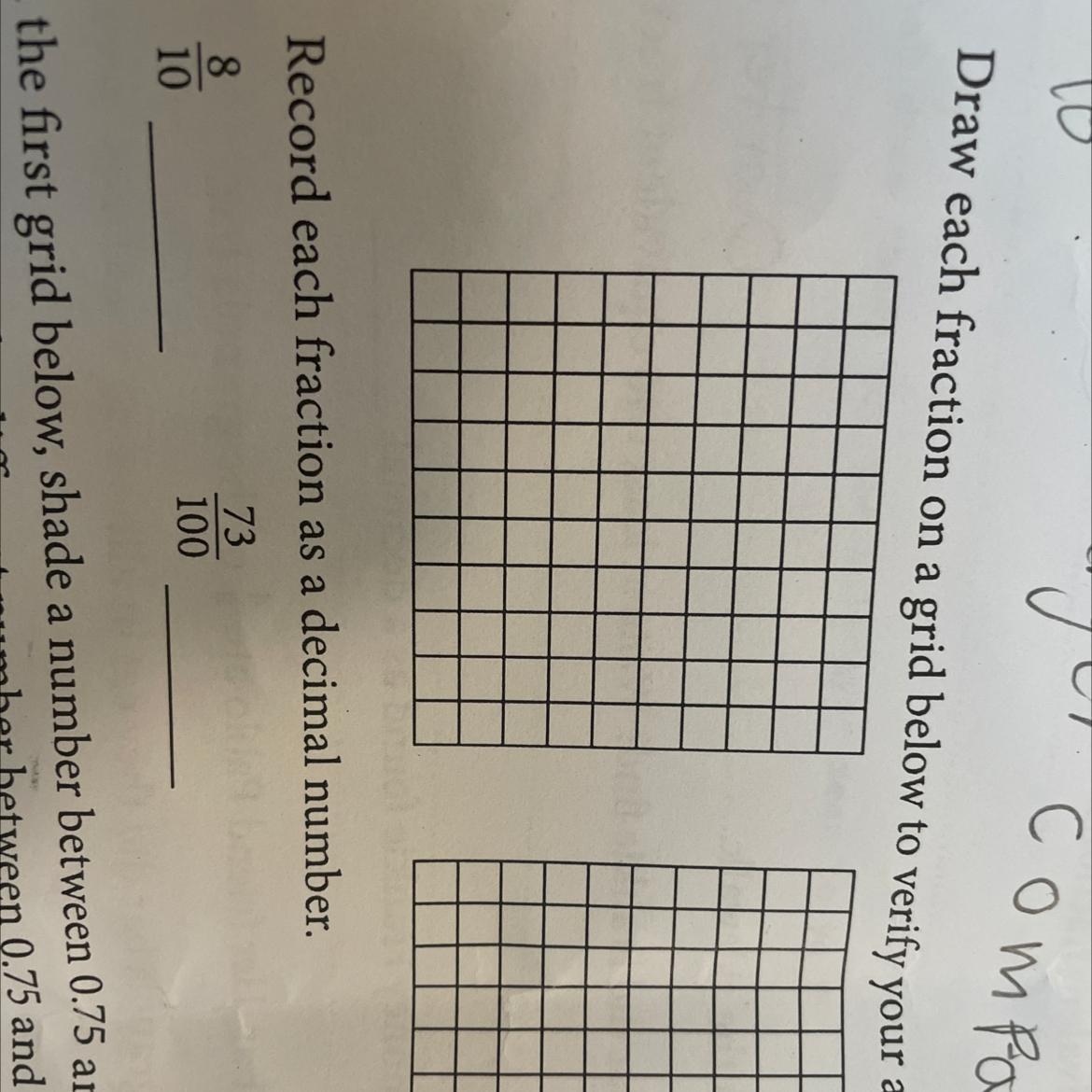
Answers
Answer:
8/10 is 0.8
73/100 is 0.73
Jenna lives 8 2/5 miles from work. Colby lives 3/4 of this distance from work. How far does Colby live from work?
Answers
Answer:
around 45 minutes
Step-by-step explanation:
it takes about 15 minutes to do 1 mile, do the correct math, it'll take about 45 minutes to do 3 miles
A 74.0 kg sprinter starts a race with an acceleration of 1.36 m/s
2
. If the sprinter accelerates at that rate for 34 m, and then maintains that velocity for the remainder of the 100 m dash, what will be his time (in s) for the race?
Answers
Given DataMass, m = 74.0 kg, Acceleration, a = 1.36 m/s²
Initial velocity, u = 0
Distance covered before constant velocity, s = 34 m
Distance remaining, s' = 100 - 34 = 66 m
Formula Used The equation for calculating distance is given by: s = ut + (1/2)at²
Where,s = Distance
u = Initial velocity
a = Acceleration
t = Time , The equation for calculating time is given by:t = √((2s)/
a)Calculation Acceleration remains constant, so the equation for calculating time will be:
t = √((2s)/a)t = √((2(34))/1.36)t = 5.11 s
Now, for calculating the remaining time taken by the sprinter to complete the race, we need to find the final velocity of the sprinter. The equation used is given by:v² - u² = 2as'
Where,v = Final velocity, u = Initial velocity, a = Accelerations' = Distance remaining
v² = u² + 2as'v² = 0 + 2(1.36)(66)v² = 179.52v = 13.4 m/sNow, we can calculate the time taken by the sprinter for the remainder of the race.t' = s'/vt' = 66/13.4t' = 4.93 s
The total time taken by the sprinter for the race is given by:Total time taken, t_total = t + t' = 5.11 + 4.93 ≈ 10.04 s
Therefore, the time taken by the sprinter to complete the race is approximately 10.04 seconds.
Learn more about acceleration from the given link
https://brainly.com/question/30660316
#SPJ11