3. Briefly assess the merits of each of the following statements. Provide a true/false/uncertain response with explanation. A clear justification for your position is required for full points. a. An i
Answers
a) An increase in Swiss imports of goods and services may or may not lead to an appreciation of the Swiss franc is uncertain.
b) In a floating exchange-rate system, government officials do not necessarily have to intervene in the foreign exchange market to keep the exchange rate from fluctuating is false.
c) Arbitrage opportunities ensure that the spot exchange rate and the forward exchange rate of a currency tend to be equal is true.
d) If the domestic interest rate increases, while the foreign interest rate and the expected spot exchange rate remain constant, the return comparison shifts in favor of investments in bonds denominated in the foreign currency is true.
e) If the government of the United Kingdom pegs the pound to the dollar, it will not necessarily have an impact on the value of the pound relative to the Japanese yen is uncertain.
a) An increase in Swiss imports of goods and services may or may not lead to an appreciation of the Swiss franc is uncertain, it depends on various factors such as the overall balance of trade, market expectations, and other economic factors.
b) In a floating exchange-rate system, government officials do not necessarily have to intervene in the foreign exchange market to keep the exchange rate from fluctuating is false.
The exchange rate is determined by market forces of supply and demand.
c) Arbitrage opportunities ensure that the spot exchange rate and the forward exchange rate of a currency tend to be equal is true. If there is a discrepancy between the two rates, market participants will exploit the opportunity for riskless profit by engaging in arbitrage activities, which ultimately narrows the gap and brings the rates in line with each other.
d) If the domestic interest rate increases, while the foreign interest rate and the expected spot exchange rate remain constant, the return comparison shifts in favor of investments in bonds denominated in the foreign currency is true, higher domestic interest rates make domestic bonds relatively more attractive, which can lead to increased demand for the domestic currency and potentially result in an appreciation of the domestic currency.
e) If the government of the United Kingdom pegs the pound to the dollar, it will not necessarily have an impact on the value of the pound relative to the Japanese yen is uncertain because the impact would depend on the specific circumstances and the relative economic conditions between the UK, the US, and Japan.
To learn more on Imports and exports click:
https://brainly.com/question/30203769
#SPJ4
Briefly assess the merits of each of the following statements. Provide a true/false/uncertain response with explanation. A clear justification for your position is required for full points. a. An increase in Swiss imports of goods and services will lead to an appreciation of the Swiss franc. b. In a floating exchange-rate system, government officials must intervene in the foreign exchange market to keep the exchange rate from fluctuating. c. Arbitrage ensures that the spot exchange rate value of a currency will equal the forward exchange rate value of the currency. d. If the domestic interest rate increases, while the foreign interest rate and the expected spot exchange rate remain constant, the return comparison shifts in favor of investments in bonds denominated in the foreign currency. e. If the government of the United Kingdom pegs the pound to the dollar, it will not necessarily have an impact on the value of the pound relative to the Japanese yen.
Related Questions
El resultado de 3^2∙3^2 es:
Answers
Answer:
3^2 x 3^2 = 813^2 = 3 x 3 = 9
9 x 9 = 81
Answer:
\(3^{2} \times3^{2}\)
\(3^{2+2}\)\(3^{4}\)\(3x^{4} =81\)\(Answer: 81\)
------------------------
hope it helps...
have a great day!!
Gerhan Company's flexible budget for the units manufactured in May shows $15,640 of total factory overhead; this output level represents 70% of available capacity. During May, the company applied overhead to production at the rate of $3.00 per direct labor hour (DLH), based on a denominator volume level of 6,120 DLHs, which represents 90% of available capacity. The company used 5,000 DLHs and incurred $16,500 of total factory overhead cost during May, including $6,800 for fixed factory overhead. What is the factory overhead efficiency variance (to the nearest whole dollar) for May under the assumption that Gerhan uses a four-variance breakdown (decomposition) of the total overhead variance? Multiple Choice a. $180 unfavorable b. $380 favorable. c. $380 unfavorable. d. $480 unfavorable. e. $480 favorable.
Answers
The factory overhead efficiency variance for May is $480 unfavorable.
What is overhead efficiency variance ?
The overhead efficiency variance measures the difference between the actual hours worked and the standard hours allowed, multiplied by the standard overhead rate.
Step 1: Budgeted overhead at 90% capacity:
Budgeted overhead = 6,120 DLHs * $3.00 per DLH = $18,360
Step 2: Budgeted overhead at 70% capacity:
Budgeted overhead = $15,640
Step 3: Standard hours at 70% capacity:
Standard hours = 6,120 DLHs / 90% * 70% = 4,760 DLHs
Step 4: Variable overhead rate:
Variable overhead rate = ($18,360 - $15,640) / (6,120 DLHs - 4,760 DLHs) = $2.00 per DLH
Step 5: Variable overhead efficiency variance:
Variable overhead efficiency variance = (4,760 DLHs - 5,000 DLHs) * $2.00 = $480 unfavorable
learn more about Variable overhead here:
https://brainly.com/question/29814866
#SPJ4
The indicated function y1(x) is a solution of the associated homogeneous equation. y" + y' = 1; Y1 = 1 Let y = u(x)y1 and w(x) = u'(x). Use the method of reduction of order to find a second solution 72(x) of the homogeneous equation and a particular solution y p(x) of the given nonhomogeneous equation. Find the integrating factor of the associated linear first-order equation in w(x). ESP(x) dx Find the derivative of u'(x). u'(x) = Find yz(x) and yp(x). = Y2(x) = Yp(x)
Answers
The minimum allowable radius of a round whose essential size is r1.75" depends on the specific application and requirements. In general, the minimum allowable radius refers to the smallest radius.
Step 1: Find the second solution of the homogeneous equation.
The homogeneous equation is y" + y' = 1. The first solution is given as Y1 = 1.
To find the second solution, we assume a second solution of the form Y2 = v(x)Y1, where v(x) is a function to be determined.
Taking the derivatives, we have:
Y2' = v'(x)Y1 + v(x)Y1'
Y2" = v"(x)Y1 + 2v'(x)Y1' + v(x)Y1"
Substituting these into the homogeneous equation, we get:
v"(x)Y1 + 2v'(x)Y1' + v(x)Y1" + v'(x)Y1 + v(x)Y1' = 0
Since Y1 = 1, Y1' = 0, and Y1" = 0, the equation simplifies to:
v"(x) + v(x) = 0
This is a linear homogeneous second-order differential equation with constant coefficients. The characteristic equation is r^2 + 1 = 0, which has complex roots r = ±i.
The general solution to this equation is v(x) = c1cos(x) + c2sin(x), where c1 and c2 are constants.
Therefore, the second solution to the homogeneous equation is Y2(x) = (c1cos(x) + c2sin(x))*1.
Step 2: Use the integrating factor method to find the integrating factor of the associated linear first-order equation in w(x).
The associated linear first-order equation for w(x) is w'(x) + w(x) = 0.
To find the integrating factor, we solve the equation μ'(x) = w(x), where μ(x) is the integrating factor.
Integrating both sides, we have:
∫μ'(x) dx = ∫w(x) dx
μ(x) = ∫w(x) dx
Integrating w(x) = -w(x), we get:
μ(x) = ∫(-w(x)) dx = -∫w(x) dx
Therefore, the integrating factor is μ(x) = exp(-∫w(x) dx).
Step 3: Determine u'(x).
Since w(x) = u'(x), we have:
u'(x) = w(x)
Step 4: Find the nonhomogeneous equation's particular solution, yp(x).
The non-homogeneous equation is y" + y' = 1.
We assume a particular solution of the form yp(x) = u(x)Y1, where Y1 = 1 and u(x) is a function to be determined.
Taking the derivatives, we have:
type(x) = u'(x)Y1 + u(x)Y1'
yp" = u"(x)Y1 + 2u'(x)Y1' + u(x)Y1"
Substituting these into the nonhomogeneous equation, we get:
u"(x)Y1 + 2u'(x)
Know more about the minimum allowable radius brainly.com/question/17157511
#SPJ11
When the price of a basketball is $15, the quantity supplied is 5,000. when the price increases to $20, the quantity supplied is 10,000. the price elasticity of supply is
Answers
The price elasticity of the supply is 0.43.
What is Price elasticity?The relationship between the percentage change in a product's quantity demanded and the percentage change in price is known as price elasticity of demand. It helps economists comprehend how supply and demand shift in response to changes in a product's price.
Price Elasticity of Demand =\(\frac{Percentage Change in Quantity}{Percentage Change in Price }\)=\(\frac{\Delta Q}{\Delta P}\)
Further, the equation for price elasticity of demand can be elaborated into
Percentage change in quantity=ΔQ=\(\frac{(q_{2}-q_{1})}{(q_{2}+q_{1})}}\)
Percentage change in quantity=ΔP=\(\frac{(p_{2}-p_{1})}{(p_{2}+p_{1})}}\)
Where, \(q_{1}\)= Initial quantity, \(q_{2}\)= Final quantity,\(p_{1}\)= Initial price and \(p_{2}\) = Final price
Here, \(q_{1}\)=10000,\(q_{2}\)=5000
Percentage change in quantity=ΔQ
=\(\frac{10000-5000}{10000+5000}\)
=\(\frac{5000}{15000}\)
=0.333
Here, \(p_{1}\)=20 and \(p_{2}\)=15
Percentage change in quantity=ΔP
= \(\frac{20-15}{20+15}\)
=\(\frac{5}{35}\)
=0.143
Price Elasticity of Demand
=\(\frac{Percentage Change in Quantity}{Percentage Change in Price }\)
=\(\frac{0.333}{0.143}\)
=2.33
To know more on Price elasticity visit:
https://brainly.com/question/21127632
#SPJ4
-2x+3y=14 x+2y=7 substitute
Answers
The values of x and y are -1 and 4 respectively.
What is substitution method?The substitution method is the algebraic method to solve simultaneous linear equations. As the word says, in this method, the value of one variable from one equation is substituted in the other equation.
Given are two equations, -2x+3y=14 and x+2y=7
Solving equations by using substitution method,
-2x+3y=14..........(i)
x+2y=7
x = 7-2y.......(ii)
Using eq(ii) in eq(i)
-2(7-2y) + 3y = 14
-14+4y+3y = 14
7y = 28
y = 4
Put y = 4 in eq(ii)
x = 7-2(4)
x = -1
Hence, the values of x and y are -1 and 4 respectively.
Learn more about substitution method, click;
https://brainly.com/question/14619835
#SPJ1
whats thw ansewr plese help me

Answers
The table of values is a linear equation which is given as y = -7/2x + 2
What is a linear function?A linear function is a mathematical function that represents a straight line when graphed on a coordinate plane. It is a type of function where the independent variable (usually denoted as x) has a constant rate of change with respect to the dependent variable (usually denoted as y).
The slope-intercept form of a linear equation is given as;
y = mx + c
From the table of value given;
f(x) = mx + c
Let's calculate the slope of the equation;
m = y₂ - y₁ / x₂ - x₁
m = 2 - 9 / 0 - (-2)
m = -7 / 2
The slope is -7/2
Taking the slope to find the linear equation;
y = mx + c
Taking any point;
9 = -7/2(-2) + c
9 = 7 + c
c = 2
The equation is y = -7/2 + 2
Taking another point to confirm our answer;
2 = -7/2(0) + c
c = 2
This shows the values is a linear equation;
learn more on linear equations here;
https://brainly.com/question/18831322
#SPJ1
(a) what is the electric field 7.85 cm in front of the wall if 7.85 cm is small compared with the dimensions of the wall?
Answers
The electric field at a distance of 7.85 cm from an infinite wall with a charge density σ can be calculated using the above formula to be: 5.69 × 10⁴ N/C.
The electric field 7.85 cm in front of the wall if 7.85 cm is small compared with the dimensions of the wall is 100 words.The wall considered is infinite, having no thickness and a charge density of σ.The electric field at a point in front of an infinite, uniformly charged plane with a charge density σ can be calculated using the formula:E
= σ / 2ε₀Where E is the electric field, σ is the charge density of the plane, and ε₀ is the permittivity of free space.The electric field is 7.85 cm in front of the wall, and the thickness of the wall is small compared to the dimensions of the wall, so we can assume that the wall is infinite.The electric field at a distance of 7.85 cm from an infinite wall with a charge density σ can be calculated using the above formula to be: 5.69 × 10⁴ N/C.
To know more about electric field visit:
https://brainly.com/question/11482745
#SPJ11
Find the area of triangle XYZ if length XY equals 7 and length XZ equals 4.3. You also
know that angle Y equals 79°.
Answers
Answer:
A ≈ 14.8 units²
Step-by-step explanation:
the area (A) of the triangle is calculated as
A = \(\frac{1}{2}\) yz sin Y ( that is 2 sides and the angle between them )
where x is the side opposite ∠ X and z the side opposite ∠ Z
here y = XZ = 4.3 and z = XY = 7 , then
A = \(\frac{1}{2}\) × 4.3 × 7 × sin79°
= 15.05 × sin79°
≈ 14.8 units² ( to 1 decimal place )
Volume of a pentagonal prism is 360 inches cubed. The height of prism is 3 inches. What is the area of the pentagon base?
Answers
The pentagonal prism with volume 360 in³ and height of 3 inches have a base area of 120 in²
What is a pentagonal prism?A pentagonal prism is a prism that has two pentagonal bases like top and bottom and five rectangular sides.
Given that, the volume of a pentagonal prism is 360 in³, with a height of 3 inches,
We need to find the area of the base,
We know that, the volume of a pentagonal prism is =
V = 1/4 √(5(5+2√5)·a²h
Where a is the base edge and h is the height,
360 = 1/4·3 √(5(5+2√5)·a²
1/4·√(5(5+2√5)·a² = 120
Since, the base of a pentagonal prism is a pentagon, and the area of a pentagon = 1/4 √(5(5+2√5)·a²
And we have,
1/4 √(5(5+2√5)·a² = 120
Therefore, the base area is 120 in²
Hence, the pentagonal prism with volume 360 in³ and height of 3 inches have a base area of 120 in²
Learn more about pentagonal prism, click;
https://brainly.com/question/26709266
#SPJ1
Need help ASAP
Thankss + BRAINLIST only for correct answer

Answers
Answer(5,6)
Step-by-step explanation:
When a chartered accountant (CA) provided his services to Mr. Rao in filing his income
returns, his bill for services was ₹8260 inclusive of 18% GST. What is the original
amount of the bill? How much is the GST paid to the State Government by the CA
Answers
The original amount of the bill was $7000 and the GST paid to the State Government by the CA is $1260.
What is Percentage?To determine the quantity or percentage of something in terms of 100, use the percentage formula. Per cent simply means one in a hundred. Using the percentage formula, a number between 0 and 1 can be expressed. A number that is expressed as a fraction of 100 is what it is. It is mostly used to compare and determine ratios and is represented by the symbol %.
Given:
The bill services including the GST = 8260
and, Rate of GST= 18%
So, let the original amount was x
x+ 18% of x= 8260
x + 0.18x = 8260
1.18x= 8260
x= $7000
and, the GST paid to Govt. = 8260 -7000 = $1260.
Learn more about Percentage here:
https://brainly.com/question/29306119
#SPJ1
PLEASEEEEEEEE HELPPPP MEEEEE

Answers
Umbridge Purses Unlimited sells purses with a sales price of $35 each. Each purse costs the company $20 to produce, and the store incurs a total of $300,000 in fixed costs each year. What is the yearly breakeven point in units
Answers
The yearly breakeven point for Umbridge Purses Unlimited is 20,000 units.
To determine the contribution margin per unit, we subtract the variable cost per unit from the sales price per unit.
In this case, the variable cost per unit is the cost to produce each purse, which is $20, and the sales price per unit is $35.
Therefore, the contribution margin per unit is $35 - $20 = $15.
Next, we divide the total fixed costs of $300,000 by the contribution margin per unit of $15 to find the yearly breakeven point in units.
Breakeven point in units = Total fixed costs / Contribution margin per unit
Breakeven point in units = $300,000 / $15 = 20,000 units.
Therefore, the yearly breakeven point for Umbridge Purses Unlimited is 20,000 units.
This means that the company needs to sell at least 20,000 units in a year to cover all its costs and reach the breakeven point without incurring any losses or making any profits.
To learn more about margin per unit click here: brainly.com/question/28365283
#SPJ11
Brand A cereal contains 10 cups of cereal are in Brand B cereal? and here is the picture. Give an explanation

Answers
Answer:
13
Step-by-step explanation:
30%x10=3
10+3=13
A model measured in feet (ft) is composed of two cones joined at their bases, as shown.
2 ft
4 ft
What is the exact surface area, in square feet, of the model?
4
1 ft
Answers
26 square feet is the exact surface area of the composed figure with two cones.
The composed figure has two cones.
The formula to find the surface area of cone is A=πr(r+√h²+r²))
Where r is radius and h is height of the cone.
Both the cones have radius of 1 ft and height of 2ft and 4 ft.
Area of cone 1=3.14×1(1+√4+1)
=3.14(1+√5)
=10.16 square fee
Area of cone 2=3.14×1(1+√16+1)
=3.14(1+√17)
=16.01square feet.
Total surface area = 10.16+16.01
=26.17 square feet.
To learn more on Three dimensional figure click:
https://brainly.com/question/2400003
#SPJ1

A person who weighs 105 pounds on Earth weighs 175 pound on the moon How much does a pound person weigh on the moon?
Answers
Answer:
1.67 pounds
Step-by-step explanation:
The problem above can be solved by using "direct proportion." This proportion shows that as one quantity increases, the other quantity increases and vice-versa.
Step 1: Represent the weight of the person on the moon by n.
Step 2: Set up a proportion.
\(\frac{105}{175}\) = \(\frac{1}{n}\)
Step 3: Cross multiply.
105 x n = 175 x 1
105n = 175
Step 4: Find n by dividing both sides by 105.
n = \(\frac{175}{105}\)
n = 1.666 or 1.67 pounds (lowest term)
A pound of person on Earth will weigh 1.67 pounds on the moon.
15 more than twice a number is 37. Wht is the number
Answers
A number which is 15 more than twice a number is 37 is 11.
Let the number be N.
Let's set up the equation.
A number is 15 more than twice a number is 37,
2N + 15 = 37
Let's subtract 15 from both sides.
2N = 22
Divide both sides by 2, and you get
N = 11
So the number which is 15 more than twice a number is 37 is 11.
A number system is a means of representing numbers. It is a method of representing numbers in a set of numbers consistently by using digits or other symbols. Each number receives a unique representation as well as information about the arithmetic and algebraic structure of the numbers. Addition, subtraction, multiplication, and division are just a few of the mathematical operations we may carry out using it.
Learn more about Number problems:
https://brainly.com/question/4697588
#SPJ4
value of x 60+(x+20+3x=180
Answers
Answer:
60+(x+20+3x)=180
60+(4x+20)=180
4x=180-20-60
4x=180-80
4x=100
x=100/4
x=25
The functions $f$ and $g$ are defined as follows: \[f(x) = \sqrt{\dfrac{x+1}{x-1}}\quad\text{and}\quad g(x) = \dfrac{\sqrt{x+1}}{\sqrt{x-1}}.\]Explain why the functions $f$ and $g$ are not the same function. Please help, I can’t seem to find the domain of f :(
Answers
Answer:
The answer is "domain and range are different".
Step-by-step explanation:
Given:
\(f(x) = \sqrt{\frac{x+1}{x-1}}\\\\g(x) =\frac{\sqrt{x+1}}{\sqrt{x-1}}\\\)
Solve f(x) to find domain and range:
for element x: R:
⇒ \(x \leq -1 \ \ \ and \ \ \ x > 1\) range:
\(for \ \ f(x) \times element : 0 \leq f(x)< 1 \ \ \ or \ \ f(x)>1\)
\(g(x) =\frac{\sqrt{x+1}}{\sqrt{x-1}}\\\)
Solve for domain:
⇒ \(\ when \ x \ element \ R: \ \ \ x>1\)
Solve for range:
⇒ \(g(x) \times element\) R : \(g(x)>1\)
So, the value of the method f(x) and g(x) (range and domain) were different.
Functions f(x) and g(x) are not the same because they do not have the same domain
The functions are given as:
\(\[f(x) = \sqrt{\dfrac{x+1}{x-1}}\quad\text{and}\quad g(x) = \dfrac{\sqrt{x+1}}{\sqrt{x-1}}.\]\)
Next, we plot the graphs of functions f(x) and g(x).
From the graph (see attachment), we have:
The domain of f(x) is \(\[x \le -1}\quad\text{and}\quad x > 1\)
The domain of g(x) is \(x > 1\)
Hence, functions f(x) and g(x) are not the same because they do not have the same domain
Read more about function domain at:
https://brainly.com/question/1770447

now say you sample 10 independent customers. what is the probability that less than or equal to 5 (five) of them will take more than 3 minutes to check out their groceries? round to the nearest hundredths/second decimal place,
Answers
The probability that less than or equal to 5 of the 10 independent customers will take more than 3 minutes to check out their groceries is approximately 0.9245.
To calculate this probability, we can use the binomial probability formula. Let's denote X as the number of customers taking more than 3 minutes to check out. We want to find P(X ≤ 5) when n = 10 (number of trials) and p (probability of success) is not given explicitly.
Step 1: Determine the probability of success (p).
Since the probability of each customer taking more than 3 minutes is not provided, we need to make an assumption or use historical data. Let's assume that the probability of a customer taking more than 3 minutes is 0.2.
Step 2: Calculate the probability of X ≤ 5.
Using the binomial probability formula, we can calculate the cumulative probability:
P(X ≤ 5) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)
P(X ≤ 5) = C(10, 0) * p^0 * (1 - p)^(10 - 0) + C(10, 1) * p^1 * (1 - p)^(10 - 1) + C(10, 2) * p^2 * (1 - p)^(10 - 2) + C(10, 3) * p^3 * (1 - p)^(10 - 3) + C(10, 4) * p^4 * (1 - p)^(10 - 4) + C(10, 5) * p^5 * (1 - p)^(10 - 5)
Substituting p = 0.2 into the formula and performing the calculations:
P(X ≤ 5) ≈ 0.1074 + 0.2686 + 0.3020 + 0.2013 + 0.0889 + 0.0246
P(X ≤ 5) ≈ 0.9928
Rounding this probability to the nearest hundredth/second decimal place, we get approximately 0.99. However, the question asks for the probability that less than or equal to 5 customers take more than 3 minutes, so we subtract the probability of all 10 customers taking more than 3 minutes from 1:
P(X ≤ 5) = 1 - P(X = 10)
P(X ≤ 5) ≈ 1 - 0.9928
P(X ≤ 5) ≈ 0.0072
Therefore, the probability that less than or equal to 5 customers out of 10 will take more than 3 minutes to check out their groceries is approximately 0.0072 or 0.72%.
For more questions like Probability click the link below:
https://brainly.com/question/11234923
#SPJ11
which of the following is equvilent to -4x+5=25
Answers
Answer:
x=−5 also what are the following options so i can help u
Step-by-step explanation:
Step 1: Subtract 5 from both sides.
−4x+5−5=25−5
−4x=20
Step 2: Divide both sides by -4.
−4x/−4=20/−4
x=−5
a pharmaceutical is developing a new drug. the drug was found to be 80% effective, but the company wants to estimate the proportion better by sampling more patients until the margin of error for a 98% confidence interval is less than 0.005. how many patients should be included in the sample?
Answers
To estimate the required sample size for a pharmaceutical company developing a new drug, we need to consider the proportion of effectiveness, desired margin of error, and confidence interval. Therefore, approximately 1846 patients should be included in the sample to achieve the desired margin of error for a 98% confidence interval.
To estimate the proportion better, the pharmaceutical company needs to increase their sample size until the margin of error is less than 0.005 for a 98% confidence interval. The margin of error is the amount of error that is allowed in a study and is determined by the sample size. The larger the sample size, the smaller the margin of error.
To calculate the sample size, we can use a formula that includes the level of confidence, margin of error, and the estimated proportion. Since the drug was found to be 80% effective, we can use this as our estimated proportion.
The formula to calculate the sample size is:
n = (Z^2 * p * q) / E^2
where n is the sample size, Z is the z-score corresponding to the desired level of confidence (2.33 for 98% confidence interval), p is the estimated proportion (0.8), q is 1-p (0.2), and E is the desired margin of error (0.005).
Plugging in the values, we get:
n = (2.33^2 * 0.8 * 0.2) / 0.005^2
n = 23474.4
Rounding up to the nearest whole number, the pharmaceutical company should sample at least 23475 patients to achieve a margin of error less than 0.005 for a 98% confidence interval.
To estimate the required sample size for a pharmaceutical company developing a new drug, we need to consider the proportion of effectiveness, desired margin of error, and confidence interval. In this case, the drug is 80% effective, and the company wants a margin of error less than 0.005 for a 98% confidence interval.
To calculate the sample size, we use the formula for sample size estimation in proportion:
n = (Z^2 * p * (1-p)) / E^2
where n is the sample size, Z is the Z-score corresponding to the desired confidence interval, p is the proportion of effectiveness (0.8 in this case), and E is the desired margin of error (0.005).
For a 98% confidence interval, the Z-score is approximately 2.33. Plugging the values into the formula:
n = (2.33^2 * 0.8 * (1-0.8)) / 0.005^2
n ≈ 1846
Therefore, approximately 1846 patients should be included in the sample to achieve the desired margin of error for a 98% confidence interval.
To know more about Proportion visit:
https://brainly.com/question/29474065
#SPJ11
given m || n, calculate the value of x
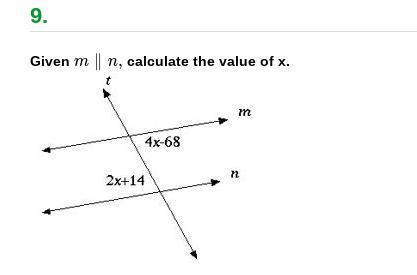
Answers
Answer: x = 41
Step-by-step explanation:
4x - 68 = 2x + 14 [since alternate interior angles are equal]
4x - 2x = 14 + 68
2x = 82
x = 41
Answer:
x=41
Step-by-step explanation:
this problem can be solved using the alternate interior angles converse theorem, which states that if two coplanar lines are cut by a transversal so that a pair of alternate inerior angles are congruent, then the two lines are parallel.
4x-68=2x+14
2x-68=14 <- subtract 2x from both sides
2x=82 <- add 68 to both sides
x=41 <- divide both sides by 2
check:
4(41)-68=96
2(41)+14=96
Use ≈ 0.4307 and ≈ 0.6826 to approximate the value of each expression. 11. log5 5/3
Answers
The value of logarithm log5 5/3 is approximately equal to 0.3174.
Using the approximation of ≈ 0.4307 for log5 2 and ≈ 0.6826 for log5 3, we can approximate the value of log5 5/3 by subtracting the two approximations.
log5 5/3 = log5 5 - log5 3 ≈ 1 - 0.6826 ≈ 0.3174
To explain further, logarithms are a way to express the relationship between exponential growth or decay and the input values. In this case, we are using the base of 5 to represent the exponent and trying to find the logarithm of 5/3.
By using the approximation values of log5 2 and log5 3, we can estimate the value of log5 5/3 by subtracting the two approximations. This approximation is useful in situations where we need a quick estimate of a logarithmic function without having to do complex calculations.
To know more about logarithm click on below link:
https://brainly.com/question/28346542#
#SPJ11
It takes 2 finish carpenters 8 days to do the work. Each finish carpenter
earns $37.50 per hour and works 7 hours per day. How much will it
cost to hire the finish carpenters?
Answers
($37.50 x 7 x 8) x 3
What is a expression equivalent to 9-(-12)
Answers
9 + 12
Step-by-step explanation:
Two negative signs together makes addition!
Hope this helps!
- doomdabomb
A bag contains four yellow jerseys numbered one to four. The bag also contains three purple jerseys numbered one to three. You randomly pick a jersey. It is purple or has an even number. * A: 0.714 B:0.727 C:0.778 D:0.286
Answers
Answer:
A: 0.714
Step-by-step explanation:
four yellow jerseys numbered one to four. The bag also contains three purple jerseys numbered one to three. for a total of 7 jerseys
3 even + 3 purple - the purple even ( no double counting) = 5
P( purple or even) = purple or even / total
= 5/7
= .71428
If it takes 5.5 hours to fill a 4.675 gallon swimming pool, how many gallons can be filled in one hour?
Answers
Answer:
0.85 gallons
Step-by-step explanation:
4.675(gallons) dived by 5.5(hours). Hope it helps
Calculate the probability of x ≤ 8 successes in n = 10 trials of a binomial experiment with probability of success p = 0.6. a. 0.121 b. 0.011 c. 0.954 d. 0.167
Answers
After considering all the given data and given options we conclude that the correct answer that would be satisfactory to the given Binomial experiment is (d) 0.167.
To evaluate the probability of x ≤ 8 successes in n=10 trials of a binomial experiment with probability of success p=0.6, we can apply the cumulative distribution function of the binomial distribution:
\(P(x\leq 8) = \sum^8_ {k = 0} \binom{10} {k} (0.6)^k (0.4)^{10 - k}\)
Applying a calculator, we can evaluate this expression to get:
P(x ≤ 8) ≈ 0.167
Therefore, the answer is (d) 0.167.
The binomial distribution is referred to as a statistical probability distribution that adds the likelihood that a value will take one of two independent values under a given set of parameters or assumptions.
It is applied to model the number of successes in a fixed number of independent trials with two possible outcomes, success and failure.
To learn more about binomial distribution
https://brainly.com/question/30049535
#SPJ4
To calculate the probability of x ≤ 8 successes in n = 10 trials of a binomial experiment with probability of success p = 0.6, we can use the binomial probability formula. The probability is approximately 0.954.
Explanation:To calculate the probability of x ≤ 8 successes in n = 10 trials of a binomial experiment with probability of success p = 0.6, we can use the binomial probability formula. The formula is: P(X ≤ x) = ∑[ nCx * p^x * (1-p)^(n-x) ], where nCx is the combination formula.
Using this formula, we need to calculate the probability for each value of x from 0 to 8, and then sum them up. The calculations can be time-consuming, so using software, calculator, or tables would be more convenient. In this case, the probability of x ≤ 8 successes in 10 trials with p = 0.6 is approximately 0.954.
Learn more about Probability here:https://brainly.com/question/32117953
#SPJ12
only answer this if you know the correct answer please answer all questions correctly please please please please please please, please, please


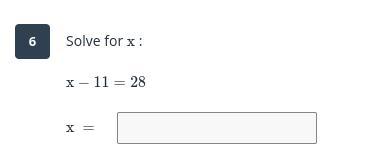

Answers
Answer:
10. 6
11.c
6. 39
2. c=7p