27. If Q is the midpoint of PR, find the coordinates of R if
P (3,-5) and Q (-1,2)?
Answers
Answer: -5,9
Step-by-step explanation:
Related Questions
One base of a trapezoid measures 12 meters, and the other base measures
8 meters. If the area is 144 square meters, what is the height of the
trapezoid?
Answers
\(Area=\frac{(a + b)}{2} \cdot h\\144 = \frac{(12 + 8)}{2} \cdot h\\144 = \frac{20}{2} \cdot h\\144 = 10h\\h = \frac{144}{10} = \frac{72}{5}\)
h=14.4m
Using the formula
A= 12 meter
B= 8 meter
H = 14.4 m
Trapezoid
Solve for height
h=14.4m
Unit Conversion:
a=12m
b=8m
A=144m²
Using the formula
A=a+b/2h
Solving for H =
Look at picture for how to work out the last part

sometimes you have to divide the diamter by 2 to get the radius.
true
false
Answers
it is true
tbh am not sure
Solve this quadratic equation by completing the square.
x^2 + 6x = 18
Answers
Step-by-step explanation:
Use formula
\( (\frac{b}{2} ) {}^{2} \)
To add a third new term and factor to find the answer. Example
\(x {}^{2} + 6x = 18\)
\(( \frac{6}{2} ) {}^{2} \)
Which equal 9. so our equation look like
\( {x}^{2} + 6x + 9 = 18 + 9\)
The only number that multiply to 9 and add up to 6 is 3. So we write our equation like this.
\((x + 3) {}^{2} = 27\)
Take the sqr root of both sides
\(x + 3 = \sqrt{27} \)
Subtract 3 from both sides
\(x = \sqrt{27} - 3\)
Since a sqr root of a number can be positive or negative, the answer is
\( \sqrt{27} - 3\)
or
\( - ( \sqrt{27} ) - 3\)
A case of woods screws wieghs 18 2/3 pounds.each individual box of woods screws wieghs 1 1/3 pounds. How many individual boxes of wood screws are in the case?
A. 5
B. 9
C. 14
D. 20
Answers
Wayne and Mack have
9 cats. Mack has twice
as many as Wayne.
How many cats does
Mack have?
Answers
Answer:
18
Step-by-step explanation:
mack has 18cats because she has 2×9 cats as Wayne 2×9 is 18
Answer:
18
Step-by-step explanation:
\(\sf Twice = *2\\9 * 2 = 18\)
An ice cream shop ordered a box of 700 cones. When they opened the box, they noticed 164 of the cones were broken. How many cones do they have left? *
Answers
Answer:
The answer would be 536 cones.
Step-by-step explanation:
You have to subtract 164 from 700.
700-164=536.
For Serenity's lemonade recipe, 4 lemons are required to make 5 cups of lemonade. At what rate are lemons being used in lemons per cup of lemonade?
Answers
For Serenity's lemonade recipe, the lemons being used per cup of lemonade is 0.8
What is ratio?Ratio is a comparison of two quantities that are expressed in relation to each other. Ratios are typically expressed in the form of a fraction, with the numerator representing one quantity and the denominator representing the other quantity.
According to question:To find the rate at which lemons are being used in lemons per cup of lemonade, we need to calculate the ratio of lemons used to cups of lemonade.
According to the recipe, 4 lemons are required to make 5 cups of lemonade. So the rate of lemons used is:
4 lemons / 5 cups = 0.8 lemons per cup of lemonade
This means that for every cup of lemonade, 0.8 lemons are used.
Alternatively, we can also express this rate as a fraction, which gives us:
0.8 lemons / 1 cup of lemonade
Either way, the rate of lemons used is 0.8 lemons per cup of lemonade.
To know more about ratio visit:
https://brainly.com/question/29192438
#SPJ1
A florist currently makes a profit of $20 on each of her celebration bouquets and sells an average of 30 bouquets every week. She noticed that when she reduces the price such that she earns $1 less in profit from each bouquet, she then sells three more bouquets per week. The relationship between her weekly profit, P(x), after x one-dollar decreases is shown in the graph below.
A graph for p of x is a downward open parabola with its vertex at (5, 725) and passes through the points (negative 10, 0), and (20, 0).
Use the graph to complete each statement about this situation.
The maximum profit the florist will earn from selling celebration bouquets is $.
The florist will break-even after one-dollar decreases.
The interval of the number of one-dollar decreases for which the florist makes a profit from celebration bouquets is ( , ).
Answers
Answer:
The maximum profit the florist will earn from selling celebration bouquets is $725.
The florist will break-even after one-dollar decreases when her profit is zero. From the graph, this occurs at x = 10. So the florist will break-even after 10 one-dollar decreases.
The interval of the number of one-dollar decreases for which the florist makes a profit from celebration bouquets is (0, 10). This is because the profit is positive for values of x between 0 and 10, and becomes negative after 10.
Step-by-step explanation:
I need to know about the fraction for this question

Answers
Answer: the fraction is 4over 12
Step-by-step explanation:
first you multiply the top and bottom number then u divide the number by the bottom.
Answer:
1/2
Step-by-step explanation:
If you were to multiply 1/2 by -50 you would get -25, which is greater than -50.
The same goes for 1/5, if you were to multiply 1/5 by -50, you would get -10.
Another example is 1/10 times -50, that would be -5.
Carlos earns $7.50 per hour cutting grass on the weekends with his dad. Last Saturday, he worked 5 and 1 over 2 hours. On Sunday he worked 8.5 hours. How much money did Carlos earn last weekend?
Answers
Answer:
$105
Step-by-step explanation:
5.5+8.5=14
14 * 7.5=105
The table shows values for functions f(x) and g(x) .
x f(x)=2^x−1 g(x)=1/2x
−2 −3/4 −1
−1 −1/2 −1/2
0 0 0
1 1 1/2
2 3 1
What is the solution to f(x)=g(x) ?
Select each correct answer.
x = −2
x = −1
x = 0
x = 1
x = 2
Answers
Answer:
x = -1
x = 0
Step-by-step explanation:
The solution to f(x) = g(x) is the value of x on the rows of the table where the value of f(x) is the same as the value of g(x). If we read your table correctly, you have ...
f(-1) = -1/2 = g(-1)
and
f(0) = 0 = g(0)
That is, f(x) = g(x) for ...
x = -1
x = 0
Solve the proportion. Show your work by typing in the steps. 9 /P-7 =8/p+10
Answers
Answer:
The proportion results to
\(p=-146\)Explanation:
Given the proportion:
\(\frac{9}{p-7}=\frac{8}{p+10}\)To solve for p, we multiply (p - 7)(p + 10)
\(\frac{9(p-7)(p+10)}{p-7}=\frac{8(p-7)(p+10)}{p+10}\)This becomes:
\(9(p+10)=8(p-7)\)Remove the brackets
\(9p+90=8p-56\)Subtract 8p from both sides
\(\begin{gathered} 9p+90-8p=8p-56-8p \\ p+90=-56 \end{gathered}\)Subtract 90 from both sides
\(\begin{gathered} p+90-90=-56-90 \\ p=-146 \end{gathered}\)Which expression is equivalent to StartRoot 8 x Superscript 7 Baseline y Superscript 8 Baseline EndRoot? Assume x greater-than-or-equal-to 0.
x y squared StartRoot 8 x cubed EndRoot
2 x cubed y cubed StartRoot x y squared EndRoot
2 x cubed y Superscript 4 Baseline StartRoot 2 x EndRoot
4 x cubed y Superscript 4 Baseline StartRoot x EndRoot
Answers
The expression that is equivalent to StartRoot \(8 x^7 y^8\) EndRoot is (\(2 x^3 y^4\) StartRoot 2 x EndRoot)^2.
To understand why this is the case, let's break down each expression and simplify them step by step:
StartRoot \(8 x^7 y^8\) EndRoot:
We can rewrite 8 as \(2^3\), and since the square root can be split over multiplication, we have StartRoot \((2^3) x^7 y^8\) EndRoot. Applying the exponent rule for square roots, we get StartRoot \(2^3\) EndRoot StartRoot \(x^7\) EndRoot StartRoot \(y^8\) EndRoot.
Simplifying further, we have 2 StartRoot \(2 x^3 y^4\) EndRoot StartRoot \(2^2\) EndRoot StartRoot \(x^2\) EndRoot StartRoot \(y^4\) EndRoot. Finally, we obtain 2 \(x^3 y^4\) StartRoot 2 x EndRoot, which is the expression in question.
(\(2 x y^2\) StartRoot 8 x^3 EndRoot)^2:
Expanding the expression inside the parentheses, we have \(2 x y^2\)StartRoot \((2^3) x^3\) EndRoot. Applying the exponent rule for square roots, we get \(2 x y^2\) StartRoot \(2^3\) EndRoot StartRoot \(x^3\) EndRoot.
Simplifying further, we have \(2 x y^2\) StartRoot 2 x EndRoot. Squaring the entire expression, we obtain (\(2 x y^2\) StartRoot 2 x EndRoot)^2.
Therefore, the expression (\(2 x^3 y^4\) StartRoot 2 x EndRoot)^2 is equivalent to StartRoot \(8 x^7 y^8\) EndRoot.
For more such questions on expression
https://brainly.com/question/1859113
#SPJ8
-62 - 4x = 42
So how do I get the answer to this problem?
Answers

Answer:
-26
Step-by-step explanation:
-62 - 4x = 42
-4x=42+62
-4x=104
X=-104/4
X=-26
So the value of the X is -26
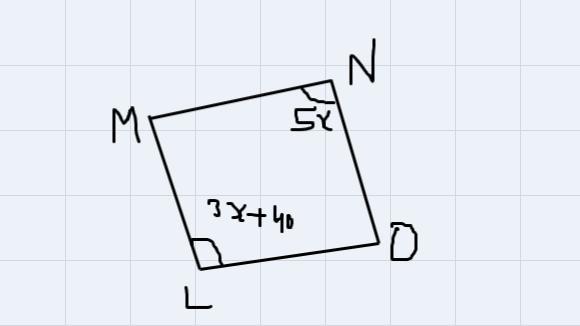
In parallelogram LNMO what is the measure of angle M?

Answers
Given
parallelogram LNMO
Find
Measure of angle M
Explanation
as we know , in parallelogram , opposite angles are equal and consecutive angles are supplementary
so ,
angle L = angle N
therefore ,
3x + 40 = 5x
2x = 40
x = 20
so ,
angle N = 5x = 100 degree
we know , the consecutive angles are supplementary.
hence , angle N + angle M = 180 degree
so , angle M = 180 - 100 = 80 degree
Final Answer
Hence , the measure of angle M is 80 degree.
-4b + 8c + 12 - 8b - 2c + 6. what is the value of the expression when b=2 and c= -3? Enter your answer.
Answers
Answer:
The answer is negative 24.
Step-by-step explanation:
(−4)(2)+(8)(−3)+12−(8)(2)+(−2)(−3)+6
=−24
I hope this helps you with your question
what is AE
AB=10
AE=2a + 10
ED=x + 3
CD=4
Enter you answer In the box
Answers
The given values into the equation AE = 2a + 10. Therefore, The value of AE is 3 - x.
To find the value of AE, we can substitute the given values into the equation AE = 2a + 10.
Given:
AB = 10
AE = 2a + 10
ED = x + 3
CD = 4
Since AB is a segment on the line, it can be divided into AE and ED. Therefore, AB = AE + ED.
We know that AB = 10 and CD = 4. So, if we subtract CD from AB, we get AE + ED = 10 - 4.
AE + ED = 6.
Now, we can substitute the value of ED, which is x + 3, into the equation: AE + x + 3 = 6.
To find the value of AE, we need to isolate it on one side of the equation. Let's subtract x and 3 from both sides:
AE = 6 - x - 3.
Simplifying further, we get;
AE = 3 - x.
Therefore, the value of AE is 3 - x.
for such more question on value
https://brainly.com/question/27746495
#SPJ8
Write y = 5(x - 8)^2 + 4 in standard form
Answers
Answer:
\(y=5x^2-80x+324\)
Step-by-step explanation:
What value of n makes the equation true
1
2
10
30
Answers
Answer:
the equation is (2x^9y^n)(4x^2y^10)=8x^11y^20
Step-by-step explanation:
,
: What is the value of y if 6y=72
Answers
Answer:
\(\rm{12}\)
Step-by-step explanation:
Hi there!
This is a one-step equation, meaning that we can solve it in one step.
This is the step:
Divide both sides by 6 in order to isolate y:
6y=72
y=12
Thus, 12 is our final answer.
Hope it helps! Enjoy your day!
\(\bold{GazingAtTheStars}\)
Answer:
\( \red\mapsto \red{6y = 72}\)
\( \red \mapsto \red{y = \frac{72}{6} }\)
\( \red \mapsto \red{y = 12}\)
describe and correct the error Teddy made in factoring x^2 -49
Both terms in the binomial are perfect
square ,so use the perfect square trinomial
pattern.
Answers
The statement that teddy made is incorrect as the expression x² - 49 can be factored using the difference of squares pattern.
What is factor?The numbers that can divide a number precisely are called factors. There is therefore no residue after division. The numbers you multiply together to obtain another number are called factors. A factor is therefore another number's multiplier.
Teddy's statement is incorrect.
The correct statement would be -
Since x² - 49 is a difference of squares, it can be factored as (x + 7)(x - 7).
Teddy's error is assuming that the factoring should involve a perfect square trinomial pattern, which is not applicable to this particular expression.
Instead, the expression can be factored using the difference of squares pattern.
The difference of squares pattern is a² - b² = (a + b)(a - b).
In this case, a = x and b = 7, so the factored form is (x + 7)(x - 7).
Therefore, Teddy's statement is wrong.
To learn more about factor from the given link
https://brainly.com/question/29151611
#SPJ1
The population of a town grows at a rate proportional to the population present at time t. The initial population of 500 increases by 10% in 10 years. What will be the population in 70 years
Answers
Answer:
974
Step-by-step explanation:
Initial × Increase percentage ^ Time
500 × (1 + 10%)^(70/10)
500 × 1.1^7
= 974.36
The population of the town in 70 years will be 974.
Find the area of the figure. (Sides meet at right angles.)
7 in
Din²
7 in
5 in
2 in
2 in

Answers
The area of the given figure is 39 square inches.
To find the area of the given figure, we can break it down into separate rectangles and then add up their areas.
The figure consists of two rectangles:
The larger rectangle with dimensions 7 in by 5 in:
Area = length × width = 7 in × 5 in = 35 in²
The smaller rectangle with dimensions 2 in by 2 in:
Area = length × width = 2 in × 2 in = 4 in²
Now, we can add the areas of these two rectangles to find the total area of the figure:
Total Area = Area of the larger rectangle + Area of the smaller rectangle
= 35 in² + 4 in²
= 39 in²
for more such questions on area
https://brainly.com/question/25292087
#SPJ8
Use decomposition to find the area of the figure.
10 yd
8 yd
The area is
13 yd
square yards.

Answers
Answer:
The area is 92 square yards.
Step-by-step explanation:
We can decompose this figure into a rectangle and a triangle.
First, we can find the area of the rectangle.
A(rect) = length × width
A(rect) = 10 × 8
A(rect) = 80 yd²
Next, we can find the area of the triangle.
A(triangle) = (1/2) × base × height
\(A(\text{triangle}) = \dfrac{1}{2} \, (13 - 10) \times 8\)
\(A(\text{triangle}) = \dfrac{3}{2} \times 8\)
\(A(\text{triangle}) = 12 \text{ yd}^2\)
Finally, we can add the two shapes' areas to get the area of the entire figure.
A = A(rect) + A(triangle)
A = 80 yd² + 12 yd²
A = 92 yd²
Answer: 92 yd²
Step-by-step explanation:
Decomposition means to break the shape into parts, but it's not necessary to break apart.
This is a trapezoid turned sideways A=1/2(b1+b1)h
b1=10
b2=13
h=8
A=1/2(10+13)8 =92 yd²
if you decompose, you can make the top a triangle and bottom a rectangle.
A(triangle) = 1/2(b)(h) b=3 h=8
1/2(b)(h)
= 12
A(rectangle)=bh b=10 h=8
=10*8
=80
Add the 2 and you get 92 again
Problem number 26 of the Rhind Papyrus says:
Find a quantity such that when it is added to StartFraction 1 Over 4 EndFraction of itself the result is a 15.
The modern day equation that models this problem is x plus StartFraction 1 over 4 EndFraction x equals 15..
What is the solution to the equation?
x = 10
x = 12
x = 15
x = 30
Answers
Answer:
X=12 on edg
Step-by-step explanation:
Answer:
I can confirm, the answer is 12.
what is 6 over square root of 8x
Answers
Answer: 0.4714
Step-by-step explanation: square root of 8 is 2.8284 divided by 6 = 0.4714.
\( \frac{6}{ \sqrt{8x} } \\ \frac{ {6}^{2} }{ {( \sqrt{8x)} }^{2} } \\ \\ \frac{36}{8x} \\ \ \\ \frac{36 \div 4}{8x \div 4} \\ \\ \frac{9}{2x} \)
this is one of the ways to simplify it
you can divide 9 by 2 the answer will be 4.5x
What is the volume of the shape below in cubic feet? Round to the nearest 10th if necessary

Answers
Step 1
State the formula for the volume of a cube
\(V=length\times width\times height\)where;
\(\begin{gathered} length=4.5ft \\ width=4.5ft \\ height=4.5ft \end{gathered}\)Step 2
Find the volume in cubic feet
\(\begin{gathered} V=4.5\times4.5\times4.5=91.125ft^3 \\ V\approx91.1ft^3to\text{ the nearest tenth} \end{gathered}\)Answer;
\(V=91.1ft^3\text{ to the nearest tenth}\)\( \: \: \: \: \: \: \: \: \: \: \: \)
![[tex] \: \: \: \: \: \: \: \: \: \: \: [/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/5pKwNW1qN0qsSwLrjpPKodTl0pJvkl4S.jpeg)
Answers
(A) (m,n) = g(n,m) for all positive integers m,n,
(B) (m,n + 1) = g(m + 1,n) for all positive integers m,n,
(D) (2m,2n) = (g(m,n))2 for all positive integers m,n
Explanation\( \rm f(m,n,p) = \sum \limits_{i = 0}^{p} {}^{m} C_{i} \: \: {}^{n + i} C_{p} \: \: {}^{p + n} C_{p - i}\)
\(\rm {}^{m} C_{i} \: \: {}^{n + i} C_{p} \: \: {}^{p + n} C_{p - i}\)
\(\rm {}^{m} C_{i} \dfrac{(n + i)!}{p!(n - p + i)!} \times \dfrac{(n + p)!}{(p - i)!(n + i)!} \)
\(\rm {}^{m} C_{i} \times \dfrac{(n + p)!}{p!} \times \dfrac{1!}{(n -p + i)!(p - i)!} \)
\(\rm {}^{m} C_{i} \times \dfrac{(n + p)!}{p!} \times \dfrac{1!}{(n -p + i)!(p - i)!} \)
\(\rm {}^{m} C_{i} \times \dfrac{(n + p)!}{p!n!} \times \dfrac{n!}{(n -p + i)!(p - i)!} \)
\(\rm {}^{m} C_{i} \: \: {}^{n + p} C_{p} \: \: {}^{n} C_{p - i} \: \: \{{}^{m} C_{i} \: \: {}^{n } C_{p - i} = {}^{m + n} C_{p } \}\)
\(\rm {}^{m} C_{i} \: \: {}^{n + p} C_{p} \: \: {}^{n} C_{p - i} \: \: \{{}^{m} C_{i} \: \: {}^{n } C_{p - i} = {}^{m + n} C_{p } \}\)
\( \rm f(m,n,p) = {}^{n + p} C_{p}{}^{m + n} C_{p}\)
\( \rm \dfrac{f(m,n,p)}{{}^{n + p} C_{p}} = {}^{m + n} C_{p}\)
Now,
\( \rm g(m,n) = \sum \limits_{p = 0}^{m + n} \dfrac{f(m,n,p)}{{}^{n + p} C_{p}} \)
\( \rm g(m,n) = \sum \limits_{p = 0}^{m + n} {}^{m + n} C_{p}\)
\( \rm g (m,n) = {2}^{m + n} \)
\( \rm(A) \: g(m,n) = q(n,m)\)
\( \rm(B) \: g(m,n + 1) = {2}^{m + n + 1} \)
\( \rm g(m + n,n ) = {2}^{m + 1 + n} \)
\( \rm(D) \: g(2m,2n) = {2}^{2m + 2n} \)
\( = \rm( {2}^{m + n} {)}^{2} \)
\( = \rm(g(m,n)) {}^{2} \)
"It was a 20% chance of rain between noon and 1pm and there is a 60% chance that the dog walker may come at that time. What percentage that the dog walker will be walking in the rain with the dogs?"
please help me with this.
I know both events are independent but I'm not sure if this is the way to solve it:
20% = 1/5
60% = 3/5
1/5*3/5= 3/25 which is 12% that both events occur at the same time
is it correct?
if not... how can I practice this? is it compound probability?
Thank you very much!
Answers
Answer:
To find the probability that both events will occur at the same time, you need to use the formula for the probability of the intersection of two events. In this case, the probability that it will rain between noon and 1pm AND that the dog walker will come at that time is:
P(Rain AND Dog Walker) = P(Rain) * P(Dog Walker | Rain)
The probability that it will rain is 20%, or 1/5. The probability that the dog walker will come at that time given that it is raining is 60%, or 3/5. Plugging these values into the formula above, we get:
P(Rain AND Dog Walker) = (1/5) * (3/5) = 3/25 = 12%
So the probability that the dog walker will be walking in the rain with the dogs is 12%.
To practice solving problems like this, you can try solving similar problems where you are given different probabilities for the two events. This will help you become more comfortable with using the formula for the probability of the intersection of two events.
Step-by-step explanation:
An oil tank has to be drained for maintenance. The tank is shaped like a cylinder that is 3 ft long with a diameter of 1.8 ft. Suppose oil is drained at a rate of 1.7 ft³ per minute. If the tank starts completely full, how many minutes will it take to empty the tank? Use the value 3.14 for pi, and round your answer to the nearest minute. Do not round any intermediate computations.
Answers
Answer:
4 minutes
Step-by-step explanation:
You want to know how long it takes to drain a cylindrical tank 1.8 ft in diameter and 3 ft long at the rate of 1.7 ft³/minute. (π = 3.14)
VolumeThe volume of a cylinder can be found using the formula ...
V = (π/4)d²h . . . . . . . diameter d, height h
Then the volume of the oil tank is ...
V = 3.14/4(1.8 ft)²(3 fft) = 7.6302 ft³
TimeThe time it takes to empty the tank is found by dividing the volume by the rate:
(7.6302 ft³)/(1.7 ft³/min) ≈ 4.49 min ≈ 4 min
It will take about 4 minutes to empty the tank.
<95141404393>
