2.6 A printer can print 12 color pages in 3 minutes. How many color pages can the printer print in 9 minutes?
Answers
Answer:
36
Step-by-step explanation:
12 times 3 = 36
Related Questions
Find the value of x in the picture below. (round to nearest tenth if needed) THANK YOU FOR HELPING ME:)
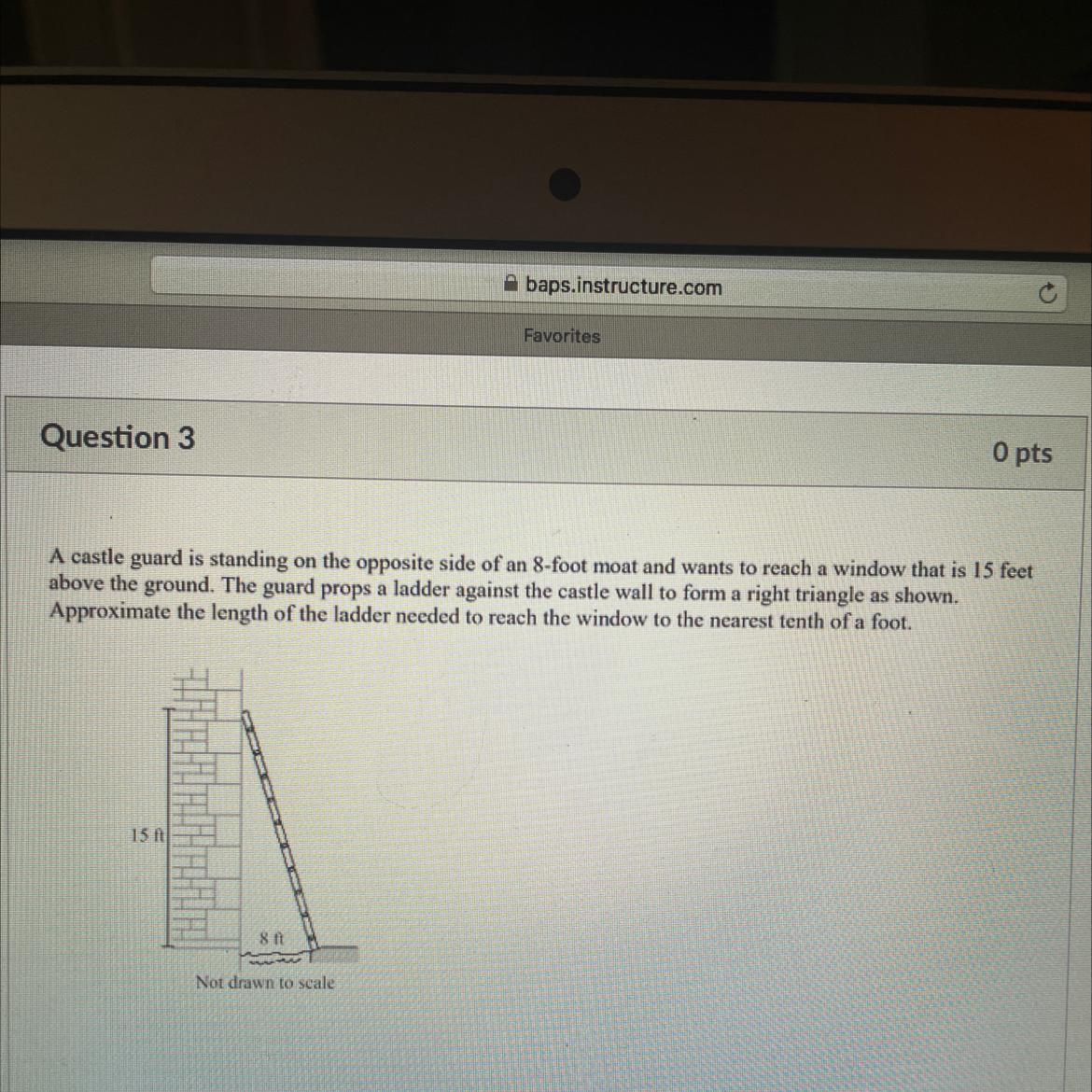
Answers
Answer:
17 feet
Step-by-step explanation:
L² = 15² + 8² = 225 + 64 = 289
L = √289 = 17 feet
Answer:
do you need the area or the perimiter?
True or False: Consider the following simple linear regression: If , then of is not biased. Group of answer choices True False
Answers
False. if there is correlation between the regressor and the error term, the estimator can be biased.
In a simple linear regression, if the regressor (independent variable) is not correlated with the error term, then the estimator of the slope coefficient will be unbiased. However, if there is correlation between the regressor and the error term, the estimator can be biased.
Therefore, without additional information about the correlation between the regressor and the error term in the given regression, we cannot determine whether the estimator is biased or unbiased.
Learn more about correlation here
https://brainly.com/question/28175782
#SPJ11
here is a scatter plot for a set of bivariate data. what would you estimate the correlation coefficient to be?
Answers
You can use scatter plots to present bivariate data. The data can be used to create coordinate pairs.
What is meant by scatter plot?The relationship between the two variables in a bivariate data set is graphically represented by a scatter plot. Consider them to be the graphic depiction of two data sets that have been combined by allocating each axis in the plot to a distinct variable.
Due to the presence of two variables, this type of data is known as bivariate data. Only 1 variable may be displayed on a line plot. You can use scatter plots to present bivariate data. The data can be used to create coordinate pairs.
The standard deviation of each variable and the covariance between them must first be determined in order to calculate the Pearson correlation. Covariance is subtracted from the product of the standard deviations of the two variables to get the correlation coefficient.
To learn more about scatter plot refer to:
https://brainly.com/question/6592115
#SPJ4
If the original quantity is 8 and the new quantity
is 2, what is the percent decrease?
Answers
If the original quantity is 8 and the new quantity is 2, then the correct answer is 75%.
How did we figure this out?
For this question we need to subtract and multiply the numbers. We know that 2 = 25% of 8 so:
\(\boxed{8-2=6}\\\boxed{6/2=3}\)
We are going to take that 25% and multiply it with 3 to get are final answer.
What is the missing number of 25 and 3?\(\boxed{25*3=75}\\\boxed{So,2=75}\)
Therefore, If the original quantity is 8 and the new quantity is 2, then the correct answer is 75%.
hello pleASE I need helppppppp

Answers
I can help you with that problem i just did that on my own.
What is the cost and area of the mat

Answers
The costs and areas of the mat are
Mat area = 2x + 2y + 4; Cost = 0.1x + 0.1y + 0.2Mat area = 4x + 4y + 16; Cost = 0.2x + 0.2y + 0.8How to determine the cost and area of the matRepresent the dimensions of the frame with
Length = x
Width = y
So, the frame area is
Area = xy
When the mat is 1 inch from the frame, we have
Whole Area = (x + 1 + 1) * (y + 1 + 1)
Whole Area = (x + 2) * (y + 2)
Expand
Whole Area = xy + 2x + 2y + 4
So, the mat area is
Mat area = xy + 2x + 2y + 4 - xy
Mat area = 2x + 2y + 4
The cost is
Cost = 0.05 * (2x + 2y + 4)
Cost = 0.1x + 0.1y + 0.2
When the mat is 2 inches from the frame, we have
Whole Area = (x + 4) * (y + 4)
Expand
Whole Area = xy + 4x + 4y + 16
So, the mat area is
Mat area = xy + 4x + 4y + 16 - xy
Mat area = 4x + 4y + 16
The cost is
Cost = 0.05 * (4x + 4y + 16)
Cost = 0.2x + 0.2y + 0.8
Read more about areas at
https://brainly.com/question/22972014
#SPJ1
Which of the following could be an example of a function with a domain
(-∞0,00) and a range (-∞,4)? Check all that apply.
A. V = -(0.25)* - 4
-
□ B. V = − (0.25)*+4
c. V = (3)* +4
□ D. V = − (3)* — 4
-

Answers
The correct options that could be an example of a function with a domain (-∞0,00) and a range (-∞,4) are given below.Option A. V = -(0.25)x - 4 Option B. V = − (0.25)x+4
A function can be defined as a special relation where each input has exactly one output. The set of values that a function takes as input is known as the domain of the function. The set of all output values that are obtained by evaluating a function is known as the range of the function.
From the given options, only option A and option B are the functions that satisfy the condition.Both of the options are linear equations and graph of linear equation is always a straight line. By solving both of the given options, we will get the range as (-∞, 4) and domain as (-∞, 0).Hence, the correct options that could be an example of a function with a domain (-∞0,00) and a range (-∞,4) are option A and option B.
Know more about function here:
https://brainly.com/question/11624077
#SPJ8
What’s the slope intercept form of (5,-5),(0,-1)
Answers
A single number that estimates the value of an unknown parameter is called a _______ estimate.
Answers
Answer:
A single number that estimates the value of an unknown parameter is called a point estimate.
Step-by-step explanation:
Don't see the point (haha) of elaborating
Math question please help me i would appreciate it !!!!
Will name brainliest

Answers
Answer:
the third one
3.F is the vertex of the pair of congruent angles i. the diagram that's all enjoy:)
Find the Present Value of Perpetuity that pays you $1,800 per
year forever assuming your money is worth 5%?
* Please be very detailed in your answer.
Answers
Therefore, the present value of the perpetuity that pays $1,800 per year forever, assuming a 5% interest rate, is $36,000. To find the present value of a perpetuity that pays $1,800 per year forever, we can use the formula:
Present Value = Cash Flow / Interest Rate
In this case, the cash flow is $1,800 and the interest rate is 5%. Plugging these values into the formula, we get:
Present Value = $1,800 / 0.05. Simplifying this equation, we find that:
Present Value = $36,000
To know more about perpetuity visit:
https://brainly.com/question/28205403
#SPJ11
The data below shows the number of people visiting a local clinic per day to be vaccinated against Measles.
5 12 19 29 35 23 15 33 37 21 26 18 23 18 13 21 18 22 20
1.1 Determine the mean of the given data. (2)
1.2 Calculate the standard deviation of the data.(2)
1.3 Determine the number of people vaccinated against Measles that lies within ONE standard deviation of the mean.(2)
1.4 Determine the interquartile range for the data.(3)
1.5 Draw a box and whiskers diagram to represent the data.(3)
1.6 Identify any outliers in the data set. Substantiate your answer.(2)
Answers
Answer:
1.3
2.5
3.7
4.95.0
5.38
6.67
Step-by-step explanation:
Answer:
Step-by-step explanation:
34
45
11
9
78
56
Which expression is equivalent to −30+(−40)+(−70) ?
−(30−40)+(−70)
−30+(−70)+(−40)
30+40+70
−30−(40−70)
Answers
Answer:
the second on 222222222222
-(30-40)+(-70) = -60
-30+(-70)+(-40) = -140
30+40+70 = 140
-30-(40-70) = 0
So your answer is -30+(-70)+(-40)
(b) Given a first order differential equation dy/dx = e^-x2 (2x+1)sinx−2xy (i) Justify if the given differential equation is linear? (ii) Identify p(x) and q(x) (iii) Find the particular solution if the initial condition is given as y(0)=5
Answers
We can evaluate the integral on the right side to find the particular solution for the given initial condition y(0) = 5.
(i) To determine if the given differential equation is linear, we need to check if the dependent variable y and its derivatives appear linearly (raised to the power of 1) and without any products or compositions. In the given differential equation dy/dx = e^(-x^2) (2x+1)sin(x) - 2xy, we can see that y and its derivative dy/dx appear linearly. Therefore, the given differential equation is linear.
(ii) In a linear first-order differential equation in the form dy/dx + p(x)y = q(x), the coefficient of y is denoted as p(x), and the right-hand side of the equation is denoted as q(x). Comparing this with the given differential equation dy/dx = e^(-x^2) (2x+1)sin(x) - 2xy, we can identify p(x) as -2x and q(x) as e^(-x^2) (2x+1)sin(x).
(iii) To find the particular solution given the initial condition y(0) = 5, we can solve the differential equation. Rearranging the given equation, we have:
dy/dx + 2xy = e^(-x^2) (2x+1)sin(x)
This is a linear first-order ordinary differential equation. We can solve it using an integrating factor. The integrating factor is given by the exponential of the integral of p(x) dx:
I(x) = e^(∫2x dx) = e^(x^2)
Multiplying the entire differential equation by the integrating factor, we get:
e^(x^2) dy/dx + 2xye^(x^2) = e^(-x^2) (2x+1)sin(x) e^(x^2)
Simplifying the left side using the product rule, we have:
d/dx (e^(x^2) y) = e^(-x^2) (2x+1)sin(x) e^(x^2)
Integrating both sides with respect to x, we obtain:
e^(x^2) y = ∫(e^(-x^2) (2x+1)sin(x) e^(x^2)) dx
The integral on the right side can be simplified as it cancels out the exponential terms:
e^(x^2) y = ∫(2x+1)sin(x) dx
Integrating the right side using integration techniques, we can find the antiderivative. Once we have the antiderivative, we divide both sides by e^(x^2) to isolate y:
y = (1/e^(x^2)) ∫(2x+1)sin(x) dx
Using numerical or numerical approximation methods, we can evaluate the integral on the right side to find the particular solution for the given initial condition y(0) = 5.
Learn more about initial from
https://brainly.com/question/31596904
#SPJ11
You and your friend go to a taco truck for lunch. You order 3 soft tacos and 3 burritos and spend $11.25. Your friend orders 4 soft tacos and 2 burritos and spends $10.00.
Answers
Answer: See explanation
Step-by-step explanation:
Let soft tacos be x
Let burritos be y
3x + 3y = 11.25 ......... i
4x + 2y = 10.00 ......... ii
Multiply equation I by 4
Multiply equation ii by 3
12x + 12y = 45 ....... iii
12x + 6y = 30 ....... iv
Subtract iv from iii
6y = 15
y = 15/6 = 2.5
A burrito cost $2.50
Since 3x + 3y = 11.25 .
3x + 3(2.50) = 11.25
3x + 7.50 = 11.25
3x = 11.25 - 7.50
3x = 3.75.
x = 3.75/3
x = $1.25
A soft tacos is $1.25
A company pays $5,000 for equipment. Annual depreciation on the equipment is $500. What is the book value of the equipment at the end of Year 2?
a. $4,000
b. $5,000
c. $6,000
d. $3,000
Answers
A company pays $5,000 for equipment. The book value of the equipment at the end of Year 2 will be $4,000.
The book value of an asset can be calculated by subtracting the accumulated depreciation from the initial cost of the asset.
Given:
Initial cost of the equipment = $5,000
Annual depreciation = $500
After Year 1, the accumulated depreciation would be $500.
So, the book value at the end of Year 1 would be:
Book value at the end of Year 1 = Initial cost - Accumulated depreciation
Book value at the end of Year 1 = $5,000 - $500 = $4,500
After Year 2, the accumulated depreciation would be $500 + $500 = $1,000 (since depreciation is $500 per year).
So, the book value at the end of Year 2 would be:
Book value at the end of Year 2 = Initial cost - Accumulated depreciation
Book value at the end of Year 2 = $5,000 - $1,000 = $4,000
Therefore, the book value of the equipment at the end of Year 2 is $4,000. Hence, the correct answer is option a. $4,000.
To know more about annual depreciation refer here;
https://brainly.com/question/30370609?#
#SPJ11
Simplify the expression:
9(-9 + -f) + -7
Submit
Answers
Answer:
-88 - 9f
Step-by-step explanation:
9(-9 + -f) + -7 = -81 - 9f - 7 = -88 - 9f
Answer:
The correct answer is -88-9f
prove the identity. sinh(2x) = 2 sinh(x) cosh(x)
Answers
To prove the identity sinh(2x) = 2 sinh(x) cosh(x), we can use the definitions of sinh(x) and cosh(x) and apply trigonometric identities for exponential functions.
We start with the left-hand side of the identity, sinh(2x). Using the definition of the hyperbolic sine function, sinh(x) = (e^x - e^(-x))/2, we can substitute 2x for x in this expression, giving us sinh(2x) = (e^(2x) - e^(-2x))/2.
Next, we focus on the right-hand side of the identity, 2 sinh(x) cosh(x). Again using the definitions of sinh(x) and cosh(x), we have 2 sinh(x) cosh(x) = 2((e^x - e^(-x))/2)((e^x + e^(-x))/2).
Expanding this expression, we get 2 sinh(x) cosh(x) = (e^x - e^(-x))(e^x + e^(-x))/2.
By simplifying the right-hand side, we have (e^x * e^x - e^x * e^(-x) - e^(-x) * e^x + e^(-x) * e^(-x))/2.
This simplifies further to (e^(2x) - 1 + e^(-2x))/2, which is equal to the expression we derived for the left-hand side.
Hence, we have proved the identity sinh(2x) = 2 sinh(x) cosh(x) by showing that the left-hand side is equal to the right-hand side through the manipulation of the exponential functions.
Learn more about Trignometric Identities here: brainly.com/question/24377281
SPJ11
a store buys 120 baseball hats at 0.50 each including tax.the store sells the hats at Markup of 50% they sell all of the hats during the season for the selling price.How much money do they receive for the sales of all the hats
Answers
Answer:
R90
Step-by-step explanation:
120 hats sold and each = $0.50
0.50 × 120 = R60 (all the baseball hats cost)
50% of 0.50 = 0.25
0.25 × 120 = 30 (markup price)
60 + 30 = 90 ( total received for the sales)
4) (3pts) Find the distance between points P_{1} and P_{2} . Show your operation: P_{1}(4,-3,-8) and P_{2}(5,-4,-9)
Answers
The distance between points P₁(4,-3,-8) and P₂(5,-4,-9) is approximately 1.732 units. This is obtained by applying the distance formula in three-dimensional space, which involves finding the square root of the sum of the squares of the differences in the coordinates of the two points. By substituting the given values into the formula and simplifying the expression, we find that the distance is approximately 1.732 units.
The distance between points P₁(4,-3,-8) and P₂(5,-4,-9) can be found using the distance formula in three-dimensional space. The calculation involves finding the square root of the sum of the squares of the differences in the coordinates of the two points.
To calculate the distance, we can use the formula:
distance = sqrt((x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²),
where (x₁, y₁, z₁) and (x₂, y₂, z₂) represent the coordinates of P₁ and P₂, respectively.
Substituting the given values into the formula, we have:
distance = sqrt((5 - 4)² + (-4 - (-3))² + (-9 - (-8))²)
= sqrt(1² + (-1)² + (-1)²)
= sqrt(1 + 1 + 1)
= sqrt(3)
≈ 1.732.
Therefore, the distance between points P₁ and P₂ is approximately 1.732 units.
Learn more about three-dimensional click here: brainly.com/question/27271392
#SPJ11
A man wants to cut down a tree in his yard. To ensure that the tree doesn’t hit anything he needs to know the height of the tree. He measures his distance from the tree at 18 meters and the angle of elevation to the tree at 80 degrees. What is the height of the tree to the nearest tenth of a meter?
Answers
Answer:
\(\boxed {\boxed {\sf 102.1 \ meters}}\)
Step-by-step explanation:
Let's assume the tree forms a right angle with the ground.
The distance from the tree to the man is 18 meters. The angle of elevation, which is 80 degrees, is the angle from where the man is to the top of the tree. We want to find the height of the tree, which we can call x.
Let's draw a diagram. (not to scale)
We can use sine (opposite/hypotenuse), cosine (adjacent/hypotenuse) or tangent (opposite/adjacent). We base the sides off of the elevation angle.
x is opposite the elevation angle and 18 is adjacent to the angle. So, we must use tangent.
\(tan(\theta)=opposite/adjacent\)
The angle (θ) is 80. The opposite is x. The adjacent is 18.
\(tan(80)=x/18\)
Now, solve for x by isolating it.
x is being divided by 18. The inverse of division is multiplication. Multiply both sides of the equation by 18.
\(18*tan(80)=x/18*18\)
\(18*tan(80)=x\)
\(18*5.67128182=x\)
\(102.0830728=x\)
Round to the nearest tenth. The 8 in the hundredth place tells us to round up.
\(102.1\approx x\)
The height of the tree is about 102.1 meters.
**diagram is not to scale

Question 10 (1 point)
Salma follows models on social media who seem to always look amazing and have
such fabulous, carefree lives. Salma wishes she could be like them and float through
live with ease. Salma's brother Khalid thinks Salma's opinion of these models is
unrealistic. What is the BEST comment Khalid could make to Salma about this?
O "Models actually have amazingly hard lives."
"These models are probably selfish and vain people."
"You don't need to be like those models to be happy."
"Those models actually aren't that attractive."
Answers
The best comment Khalid could make to Salma about her opinion of the models she follows on social media is: "You don't need to be like those models to be happy." (Option C).
How to Determine the Comment?The chosen comment above comment is determined to be the best because it offers a constructive and positive perspective to Salma, while acknowledging her desire to emulate the models she follows on social media. It encourages her to shift her focus away from comparing herself to others and towards finding her own path to happiness.
The other options, such as "Models actually have amazingly hard lives" and "Those models actually aren't that attractive," are not helpful or constructive comments. They either discredit the hard work and dedication that models put into their careers or offer a negative perspective on their physical appearance. These comments are unlikely to make Salma feel better about herself or improve her outlook on the situation.
The comment "These models are probably selfish and vain people" is also not helpful because it makes an assumption about the models' personalities based solely on their social media presence, which is not necessarily accurate or fair.
Learn more about comment here: https://brainly.com/question/30026509
#SPJ1
Rewrite the following equation in slope intercept form Y+10= 1/4 (x+8)
Answers
Answer:
y=1/4x-8
Step-by-step explanation:
pemdas just move y to the side
What does x equal in the question
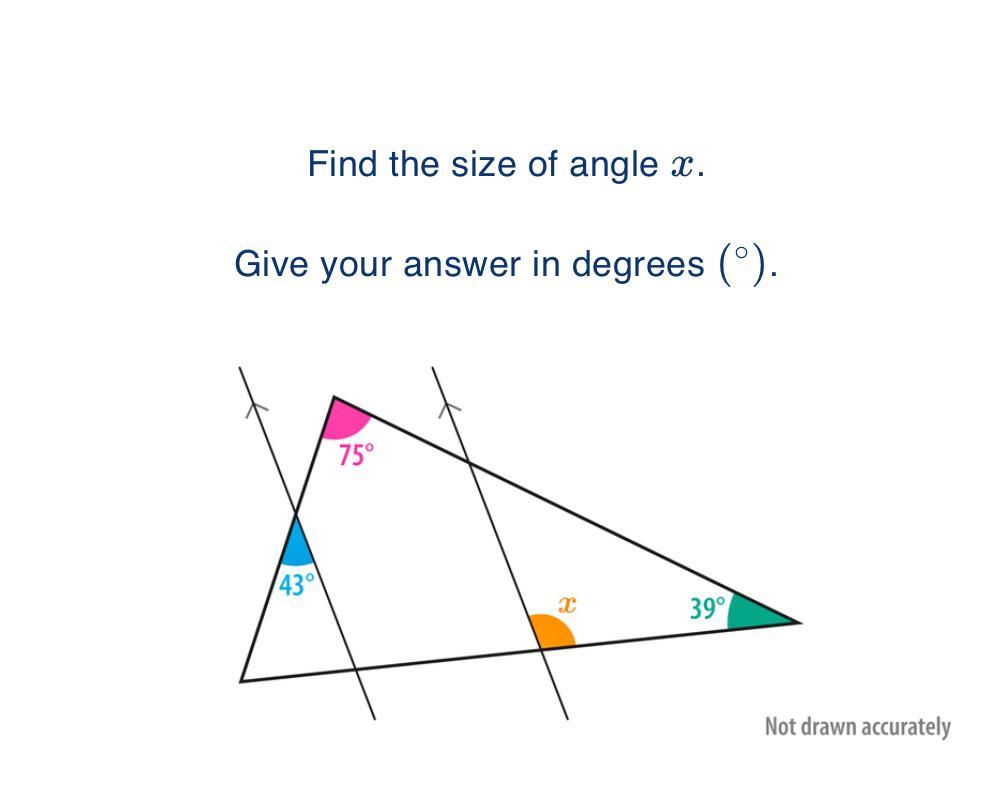
Answers
Answer:
Step-by-step explanation:
75
w/4 = -11
please help !!!
Answers
5. Problem 5.15 (Present Value of an Annuity) Find the present values of these ordinary annuities. Discounting occurs once a year. Do not round intermediate calculations. Round your answers to the nearest cent. a. $400 per year for 14 years at 14%. $ b. $200 per year for 7 years at 7%. $ c. $400 per year for 7 years at 0%. $ d. Rework previous parts assuming they are annuities due. Present value of $400 per year for 14 years at 14%:$ Present value of $200 per year for 7 years at 7% : $ Present value of $400 per year for 7 years at 0% : $
Answers
a. Present value of $400 per year for 14 years at 14%: $2,702.83
b. Present value of $200 per year for 7 years at 7%: $1,155.54
c. Present value of $400 per year for 7 years at 0%: $2,800
d. Present value of $400 per year for 14 years at 14% (annuity due): $2,943.07
Present value of $200 per year for 7 years at 7% (annuity due): $1,233.24
Present value of $400 per year for 7 years at 0% (annuity due): $2,800
To find the present values of the ordinary annuities, we can use the formula for the present value of an annuity:
PV = PMT * [(1 - (1 + r)^(-n)) / r]
Where:
PV = Present value
PMT = Payment per period
r = Interest rate per period
n = Number of periods
a. $400 per year for 14 years at 14%:
PV = $400 * [(1 - (1 + 0.14)^(-14)) / 0.14]
≈ $2,702.83
b. $200 per year for 7 years at 7%:
PV = $200 * [(1 - (1 + 0.07)^(-7)) / 0.07]
≈ $1,155.54
c. $400 per year for 7 years at 0%:
Since the interest rate is 0%, the present value is simply the total amount of payments over the 7 years:
PV = $400 * 7
= $2,800
d. Reworking previous parts assuming they are annuities due:
For annuities due, we need to adjust the formula by multiplying it by (1 + r):
a. Present value of $400 per year for 14 years at 14%:
PV = $400 * [(1 - (1 + 0.14)^(-14)) / 0.14] * (1 + 0.14)
≈ $2,943.07
b. Present value of $200 per year for 7 years at 7%:
PV = $200 * [(1 - (1 + 0.07)^(-7)) / 0.07] * (1 + 0.07)
≈ $1,233.24
c. Present value of $400 per year for 7 years at 0%:
Since the interest rate is 0%, the present value remains the same:
PV = $400 * 7
= $2,800
In conclusion:
a. Present value of $400 per year for 14 years at 14%: $2,702.83
b. Present value of $200 per year for 7 years at 7%: $1,155.54
c. Present value of $400 per year for 7 years at 0%: $2,800
d. Present value of $400 per year for 14 years at 14% (annuity due): $2,943.07
Present value of $200 per year for 7 years at 7% (annuity due): $1,233.24
Present value of $400 per year for 7 years at 0% (annuity due): $2,800
To know more about formula visit
https://brainly.com/question/867780
#SPJ11
How many solutions does 7(x - 2) + 5 = 3 (2x - 1) + 1 have?
Answers
Answer:
one, x = 7
Step-by-step explanation:
7(x - 2) + 5 = 3 (2x - 1) + 1
reduce:
7x - 14 + 5 = 6x - 3 + 1
x = 7
Help is much needed. You will get lots of point too!

Answers
500m of fencing is available to make 4 rectangular pens of identical shape. Find the dimensions that maximise the area of each pen if the plan is: (DIAGRAMS BELLOW)

Answers
Answer:
The answer is "\(x(\frac{250}{3}-x)\)"
Step-by-step explanation:
Both points are similar that's why the solution is:
\(\to \frac{6x+6y=500}{6}\\\\\to x+y=\frac{250}{3}\\\\\to y= \frac{250}{3}-x \\\\\to Area= xy\\\\ \to Area= x(\frac{250}{3}-x)\)
please help me with the ratio

Answers
Answer:
total number of votes = 5696
Step-by-step explanation:
the 5 part of the ratio relates to 3560 no votes , then
3560 ÷ 5 = 712 ← value of 1 part of the ratio , then
3 × 712 = 2136 ← number of yes votes
total number of votes = yes + no = 2136 + 3560 = 5696