2 questions I need help with !
The grams of fiber from 1,000 different breakfast cereals sold in the United States were collected.
Which graphical representation would be most appropriate for the data, and why?
A Bar chart, because the data is categorical
B Histogram, because there is a large set of data
C Stem-and-leaf plot, because you can see the shape of the data
D Line plot, because you can see the mode of the data
——-
At a recent baseball game of 5,000 in attendance, 150 people were asked what they prefer on a hot dog. The results are shown.
Ketchup Mustard Chili
63 27 60
Based on the data in this sample, how many of the people in attendance would prefer mustard on a hot dog?
A 900
B 2,000
C 2,100
D 4,000
Answers
The required,
(A) Option B. Histogram, because there is a large set of data, is correct.
(B) The requried, 900 people in attendance would prefer mustard on a hot dog
A,
Since the fiber data is a continuous numerical variable and the data set is large, it would be difficult to summarise with a bar chart or stem-and-leaf plot. A histogram would be the most appropriate graphical representation of the fiber data. We may visualize the distribution of the data using a histogram by grouping the data into intervals (bins).
B.
We can make the assumption that the sample is typical of the population and use proportions to calculate the approximate number of attendees who would prefer mustard on a hot dog.
The percentage of respondents that like mustard on their hot dogs is:
27/150 = 0.18
We may multiply this fraction by the total number of attendees to get an idea of how many attendees would like mustard on a hot dog:
0.18 x 5000 = 900
Therefore, Option A is correct.
Learn more about Histogram here:
https://brainly.com/question/30354484
#SPJ1
Related Questions
How do you solve 14p−8=22+20p ?
Answers
The value of p is -5
Simply use cross multiplication :
The process of multiplying numbers in the shape of a fraction is called cross multiplication. Cross multiplying, also known as cross multiplication, is the process of multiplying the numerator of one fraction by the denominator of the other fraction on the other side of an equal symbol. Cross multiplication is a method for comparing fractions.
Both fractions with like and unlike parts are multiplied across. When employing the cross-multiplication procedure, we multiply the denominators as well as the numerators when a fraction is dissimilar, or when the denominators of two fractions are not alike.
\(14p-8=22+20p\\or, 14p-20p=22+8\\or, -6p=30\\or, p=-\frac{30}{6} \\or, p= -5\)
To learn more about cross multiplication visit: brainly.com/question/29190202
#SPJ4
PLZ HELP OMG!! I’ll mark Brainliest to whoever gives correct answer first!!!

Answers
Answer:
Step-by-step explanatioThe chosen topic is not meant for use with this type of problem. Try the examples below.
2
(
x
2
−
1
)
=
16
,
(
0
,
4
)
8
=
2
(
3
x
+
3
)
2
,
(
−
1
,
3
)
x
(
x
+
4
)
=
24
,
(
−
2
,
9
)
n:
Kevin divides 3 pieces of paper into fourths.
How many fourths does he have? *
Answers
Answer:
12
Step-by-step explanation:
if you have three WHOLE sheets, and you divide them into fourths... 4 times 3, equals 12. Brainly please. :)
Answer:
12 fourths
\(\frac{12}{4}\)
Step-by-step explanation:
If one paper is divided by 4 you have 4 fourths, now you multiply 4 by three and you get 12.
So twelve-fourths is your answer.
Hope this helps and have a great day!
of a pizza remains, and Seth and Ethan want to split it evenly. What fraction of the original pizza will each get?
Answers
Answer:
\(\huge\boxed{\text{Multiply the denominator by 2, or}}\\\\\huge{\boxed{\text{divide the percentage by 2}}}}\)
Step-by-step explanation:
Because there is no fraction or percentage given, simply follow this rule to divide a portion by 2.
Hope it helps :) and let me know if you want me to elaborate(solve with fraction)
Machine Total Defectives #1 23 #2 15 #3 29 #4 13 What is the estimate of the standard deviation of the sampling distribution of sample proportions for this process?
Answers
Answer:
The estimate of the standard deviation of the sampling distribution of sample proportions for this process is approximately 0.1265.
Given that the machine total defectives are #1=23, #2=15, #3=29 and #4=13
To find the estimate of the standard deviation of the sampling distribution of sample proportions for this process Formula used:
The formula for the standard deviation of the sampling distribution of sample proportions is given by the expression as, SD = √(pq/n)
Where, p = the proportion of successes
q = the proportion of failures
n = the sample size
Substitute the values in the formula
SD = √(pq/n)p
= 80/100
= 0.8 (as there are 80 defectives out of 100 items produced.)
q = 20/100 = 0.2 (as there are 20 non-defectives out of 100 items produced.)
n = Sample size = 100
Thus, SD = √(pq/n)SD
= √(0.8*0.2/100)SD
= √(0.016)SD
= 0.1265 (approximately)
Therefore, the estimate of the standard deviation of the sampling distribution of sample proportions for this process is approximately 0.1265.
To learn more about standard deviation of sampling distribution,visit here
https://brainly.in/question/8762503
#SPJ11
g(x)=2x+1
h(x)=x3−x2
g(h(2))=
Answers
Answer:
9
Step-by-step explanation:
g(h(2))= 2(x3-x2)+1 = 2(2^3-2^2)+1 = 2(8-4)+1
=2*4+1 = 9
1.If a shirt costs 60 dollars, it's marked down to 20% off, what is the amount of the discount?
Answers
Answer:
$12.00
Step-by-step explanation:
20% of $60 is $12.
Sasha needs to write a division expression for the fraction 9/14. She is not sure which number goes where. Help Sasha understand how to write a division expression from a fraction
Answers
To write a division expression from a fraction, identify the numerator, which is the dividend, while the denominator is the divisor.
What is a division expression?A division expression is an algebraic expression using the division operand (÷).
Algebraic expressions involve the combination of numbers, constants, values, and variables with mathematical operands.
The result of a division operation, which is one of the four basic mathematical operations, is known as the quotient.
Thus, we can conclude that the dividend is related to the numerator of the fraction just as the divisor is related to the denominator of the fraction.
Learn more about division expressions at https://brainly.com/question/30293049.
#SPJ1
solve simultaneously
\( {2}^{x} + {3}^{y} = 9 \\ {2}^{x + 2} - {3}^{y + 1} = 8\)
Answers
Answer:
I hope this helps you :)
![solve simultaneously[tex] {2}^{x} + {3}^{y} = 9 \\ {2}^{x + 2} - {3}^{y + 1} = 8[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/3rWVlipNgZY52uTA8rmilWAXlvhL64C5.png)
![solve simultaneously[tex] {2}^{x} + {3}^{y} = 9 \\ {2}^{x + 2} - {3}^{y + 1} = 8[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/HMKpacYWv5wm3cYaafMp3xrdTTavLFZg.png)
Answer:
2x+3y=9
2x+2-3y+1=8
2x-3y=8
2x-3y+3y=8+3y
2x=8+3y
2x=8+3y
2 2
x=8+3y
2
2(x) +3y=9
2* (8+3y)/2 +3y=9
(16+6y)/2)+3y=9
2*(16+6y)/2)+3y=9
16+6y+6y=18
6y+6y=18-16
12y=2
12y = 2
12 12
y=2
12
y=0.16666666666667
2x+3 (0.16666666666667)=9
2x+0.5=9
2x=9-0.5
2x=8.5
2x = 8.5
2 2
x=8.5
2
x=4.25
Figure ABC is reflected over the x-axis to obtain figure A′B′C′ below: Triangle ABC is located on the coordinate plane with vertex A at negative 5 comma 4, vertex B at negative 2 comma 4, and vertex C at negative 4 comma 1. Triangle A prime B prime C prime is located with vertex A prime at negative 5 comma negative 4, vertex B prime at negative 2 comma negative 4, and vertex C prime at negative 4 comma negative 1. Which statement best describes the relationship between the two figures? (5 points) Figure ABC is bigger than figure A′B′C′. The measure of angle A is equal to the measure of angle B′. The measure of angle C is equal to the measure of angle B′. Figure ABC is congruent to figure A′B′C′.
Answers
Answer:
Figure ABC is congruent to figure A′B′C′.
Step-by-step explanation:
I just did the test and got it right
D - Figure ABC is congruent to figure A′B′C′.
Step-by-step explanation
took the test
I’m struggling help ASAP

Answers
Answer:
see explanation
Step-by-step explanation:
The n th term of an arithmetic sequence is
\(a_{n}\) = a₁ + (n - 1)d
where a₁ is the first term and d the common difference
Here a₁ = 40 ( first row )
d = - 4 ( 4 fewer than the row below ), thus
\(a_{n}\) = 40 - 4(n - 1) = 40 - 4n + 4 = 44 - 4n
That is
\(a_{n}\) = 44 - 4n
(b)
a₁₀ = 44 - 4(10) = 44 - 40 = 4
There are 4 boxes on the 10 th row
At the start of the week, Crystal’s bank account had a balance of $280. Each day from Monday to Friday, she used her debit card to pay $5 for parking. She wrote a check for $42, and made two deposits of $75 each. She also withdrew $200 in cash at an ATM. What was Crystal’s balance at the end of the week?
Evaluate the expression below to solve the problem.
280 + 5(–5) + (–42) + 2(75) + (–200)
$ = ??
Answers
Answer:
280 + 5(–5) + (–42) + 2(75) + (–200)
=163
Step-by-step:
Each day from Monday to Friday, she used her debit card to pay $5 for parking so we do
5×5=25 just for parking
then we take away 25 pounds from 280 to find out how much she has now which is
255
then...
She wrote a check for $42,
so
255-42= 213
and made two deposits of $75 each and she also withdrew $200 in cash at an ATM
213+75+75= 363
363-200= 163
this makes her balance at the end of the week 163
Hope this helped you-have a good day bro cya)
Crystal’s balance at the end of the week is $163.
What is an expression?Expressions in math are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between.
Given expression
280 + 5(–5) + (–42) + 2(75) + (–200)
= \(280 - 25 - 42 + 150 - 200\)
= \(280 +150-42-25-200\)
= \(430-42-25-200\)
= \(388-25-200\)
= \(363-200\)
= \(163\)
Crystal’s balance at the end of the week is $163.
Find out more information about expression here
https://brainly.com/question/14083225
#SPJ2
Algebraically solve for x:
7/2x - 2/x+1 = 1/4

Answers
The value of x in the algebraic equation 7 / 2x - 2 / x + 1 = 1 / 4 is 7 and -2
How to solve algebraic equation?let's find the value of x in the algebraic equation.
7 / 2x - 2 / x + 1 = 1 / 4
Therefore, let's solve the left side.
7 / 2x - 2 / x + 1 = 7(x + 1) - 4x / 2x(x + 1) = 7x + 7 - 4x / 2x² + 2x = 3x + 7 / 2x² + 2x
3x + 7 / 2x² + 2x = 1 / 4
cross multiply
4(3x + 7) = 2x² + 2x
12x + 28 = 2x² + 2x
2x² + 2x - 12x - 28 = 0
2x² - 10x - 28 = 0
x² - 5x - 14 = 0
Therefore,
(x + 2)(x - 7)
hence,
x = -2 or x = 7
learn more on algebraic equation here: https://brainly.com/question/7194400
#SPJ1
using dijkstra’s algorithm, find the sink tree rooted at vertex 7.
Answers
Dijkstra's algorithm calculates the shortest path from vertex 7 to all other vertices in the graph, forming a tree structure where vertex 7 is the root.
Dijkstra's algorithm is a graph traversal algorithm used to find the shortest path between two vertices in a weighted graph. To find the sink tree rooted at vertex 7, we can apply Dijkstra's algorithm starting from vertex 7. The algorithm proceeds by iteratively selecting the vertex with the smallest distance from the current set of vertices and updating the distances to its adjacent vertices.
Starting from vertex 7, we initialize the distance of vertex 7 as 0 and the distances of all other vertices as infinity. Then, we explore the adjacent vertices of vertex 7 and update their distances accordingly. We repeat this process, selecting the vertex with the smallest distance each time, until we have visited all vertices in the graph.
The result of applying Dijkstra's algorithm to find the sink tree rooted at vertex 7 is a tree structure that represents the shortest paths from vertex 7 to all other vertices in the graph. Each vertex in the tree is connected to its parent vertex, forming a directed acyclic graph. This sink tree provides a clear visualization of the shortest paths and their corresponding distances from vertex 7 to each vertex in the graph.
Learn more about acyclic graph here:
https://brainly.com/question/31861982
#SPJ11
WILL MARK BRAINLIEST!
arrange -2, 1.8, -1/3, -1/4, √5 at descending order
Answers
Answer:
√5, 1.8, -1/4,-1/3,-2
Step-by-step explanation:
Please put brainliest if this helps
Answer:
sqrt5, 1.8, -1/4, -1/3 and -2
Step-by-step explanation:
I. Find the true value of variables
-2 = -2
1.8 = 1.8
-1/3 = -0.333...
-1/4 = -0.25
sqrt5 = 2.236
II. Descending is most to least so
= 2.236, 1.8, -0.25, -0.333, -2
or sqrt5, 1.8, -1/4, -1/3 and -2
For -0.x, if x is near 0 will be the greatest value,
and +0.x if x is far from 0 will be the greatest value
So Descending is sqrt5, 1.8, -1/4, -1/3 and -2
the magnification of a convex mirror is 0.67 times for objects 3.8 m from the mirror. What is the focal length of this mirror?
Answers
Magnification of a convex mirror is 0.67 times for objects 3.8 m from the mirror .the focal length is negative, this means that the mirror is a diverging mirror (convex mirror). Therefore, the focal length of this mirror is 2.4 meters.
To find the focal length of a convex mirror, we can use the mirror formula:
1/f = 1/v + 1/u
where f is the focal length, v is the image distance, and u is the object distance.
In this case, we know that the magnification (M) of the mirror is 0.67, and the object distance (u) is 3.8 m. We also know that for a convex mirror, the image is always virtual and upright, so the image distance (v) is negative.
The magnification formula is:
M = -v/u
Substituting the values we have:
0.67 = -v/3.8
v = -2.546 m
Now we can use the mirror formula to find the focal length:
1/f = 1/-2.546 + 1/3.8
1/f = -0.416
f = -2.4 m
Since the focal length is negative, this means that the mirror is a diverging mirror (convex mirror). Therefore, the focal length of this mirror is 2.4 meters.
To know more about Magnification visit :
https://brainly.com/question/20368024
#SPJ11
help pleasee
solve i^100 - i^80 if i^2 = -1 and i^3 = -i
Answers
Answer:
Step-by-step explanation:
\(i^{100} - i^{80}=i^{2*50} -i^{2*40}\\\\=(i^{2})^{50}-(i^{2})^{40}\\\\=(-1)^{50}-(-1)^{40}\\\\\)
= 1 - 1
= 0
(a) Sketch two approximate solutions of the differential equation on the slope field, one of which passes through the indicated point.(b) Use integration to find the particular solution of the differential equation and use a graphing utility to graph the solution. Compare the result with the sketches in part (a).
dydx=cosx,(0,4)
dydx=cosx,(0,4)
Answers
We can make use of a slope field to sketch the two approximate solutions of the differential equation. The slope field for the differential equation is dy/dx.
a) We will now mark the point (0,4) on the slope field as shown in the image below.
Now we will sketch two approximate solutions of the differential equation on the slope field, one of which passes through the indicated point (0, 4).Solution 1: We will begin at the point (0, 4) and move along the slope lines to obtain the first solution. This first solution is shown in blue in the image below,
Solution 2: For the second solution, we will begin at the point (0,4) and move along the slope lines in the opposite direction to obtain the second solution. This second solution is shown in red in the image below.
We have thus sketched two approximate solutions of the differential equation on the slope field, one of which passes through the indicated point (0,4).b) We can make use of integration to find the particular solution of the differential equation dy/dx = cos(x). We will begin by integrating both sides with respect to X. We get: y = sin(x) + CTo find the value of C, we will make use of the initial condition (0,4).Substituting x = 0 and y = 4, we get: 4 = sin(0) + C4 = 0 + CC = 4
Therefore, the particular solution is: y = sin(x) + 4
We will now use a graphing utility to graph the solution.Below is the graph of the solution: Graph of y = sin(x) + 4
We can compare this graph of the particular solution with the sketches in part (a).
The graph of the solution matches the first solution in blue.
To learn more about “utility” refer to the https://brainly.com/question/14729557
#SPJ11
.
Find the measure of ∠3.
45°
90°
135°
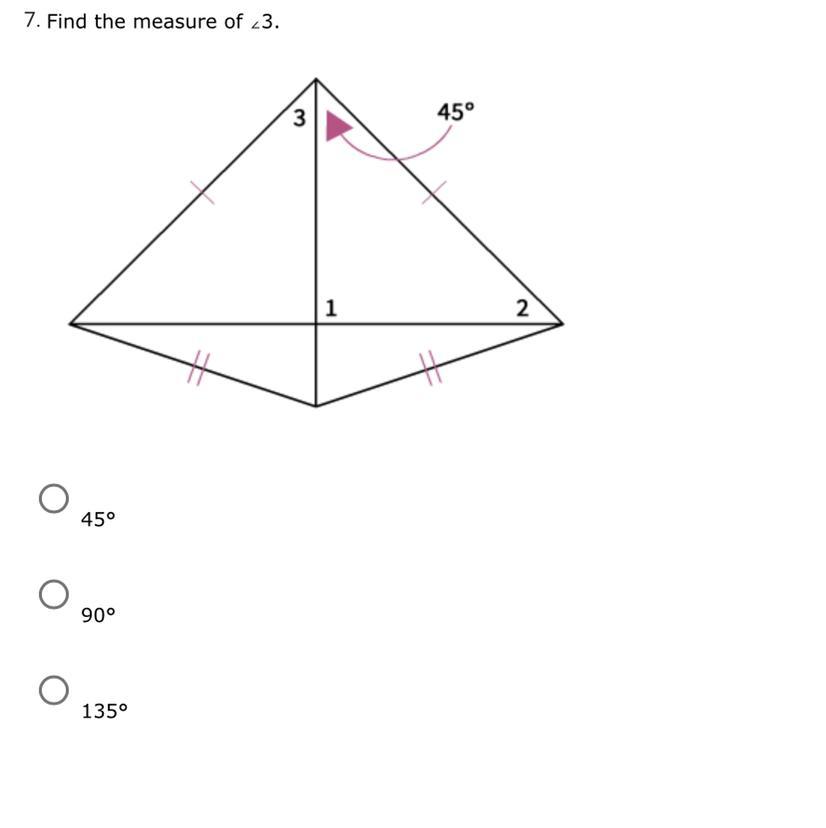
Answers
7.4.2. what values of x satisfy the following equations? (a) p(−x ≤ t22 ≤ x) = 0.98
Answers
The values of x that satisfy the equation p(−x ≤ t22 ≤ x) = 0.98 are all values between -2.518 and 2.518, inclusive.
The expression p(- x ≤ t22 ≤ x) represents the probability of a t-distribution with 22 degrees of freedom lying between - x and x.
We want to find the values of x such that this probability is 0.98.
We can use a table of t-distribution probabilities or a calculator to find the value of t for which the probability of a t-distribution with 22 degrees of freedom lying between −t and t is 0.98.
This value is , 2.518.
Therefore, we need to solve the inequalities:
-2.518 ≤ -x ≤ 2.518
Solving for x, we get:
-2.518 ≤ -x x ≤ 2.518
Therefore, the values of x that satisfy the equation p(−x ≤ t22 ≤ x) = 0.98 are all values between -2.518 and 2.518, inclusive.
Learn more about the inequality visit:
https://brainly.com/question/25944814
#SPJ12
LINEAR DIOPHANTINE EQUATIONS 2) Determine the integral solutions for which x and y are positive. 2x + 5y = 17
Answers
The positive integral solutions for the equation 2x + 5y = 17 are:
x = 5n + 6, y = -2n + 1, where n ≥ 0.
To find integral solutions for the linear Diophantine equation 2x + 5y = 17, where x and y are positive, we can use a systematic approach called the Euclidean algorithm.
Step 1: Find the general solution of the associated homogeneous equation.
The associated homogeneous equation is 2x + 5y = 0. The general solution can be written as x = 5n and y = -2n, where n is an integer.
Step 2: Find a particular solution for the given equation.
To find a particular solution, we can start with x = 6 and solve for y:
2x + 5y = 17
2(6) + 5y = 17
12 + 5y = 17
5y = 5
y = 1
So, a particular solution is x = 6 and y = 1.
Step 3: Find the complete set of positive integral solutions.
To find the positive integral solutions, we can add the general solution to the particular solution while ensuring x and y are positive.
x = 5n + 6
y = -2n + 1
To satisfy the condition of positive values, we can set n ≥ 0.
Therefore, the positive integral solutions for the equation 2x + 5y = 17 are:
x = 5n + 6, y = -2n + 1, where n ≥ 0.
Learn more about integrals here:
https://brainly.com/question/30094386
#SPJ11
Find the volume of the solid formed by rotating the region in the 1st quadrant enclosed by the curves y=x^1/4 and y=x/64 about the y-axis
Answers
The volume of the solid is (3π/5) units^3. To find the volume of the solid formed by rotating the region in the 1st quadrant enclosed by the curves y=x^1/4 and y=x/64 about the y-axis, we can use the method of cylindrical shells.
First, we need to determine the limits of integration. Since the region is in the 1st quadrant, we can integrate from y=0 to y=1. To find the corresponding x-values for these limits, we can set y=x^1/4 and y=x/64 equal to 1 and solve for x:
x^1/4 = 1 => x = 1
x/64 = 1 => x = 64
So, our limits of integration are x=1 to x=64.
Next, we need to find an expression for the radius of each cylindrical shell. The radius is simply the distance from the y-axis to the curve at a given y-value. So, for a given y, the radius is:
r = x - x^1/4
Finally, we need to find an expression for the height of each cylindrical shell. The height is the infinitesimal change in y, which is simply dy. So, the volume of each cylindrical shell is:
dV = 2πr dy
Putting it all together, we have:
V = ∫(2πr) dy from y=0 to y=1
= ∫2π(x - x^1/4) dy from y=0 to y=1
= 2π ∫(x - x^1/4) dy from y=0 to y=1
= 2π ∫(y^4 - y) dy from y=0 to y=1
= 2π [y^5/5 - y^2/2] from y=0 to y=1
= 2π [(1/5) - (1/2)]
= (3π/5) units^3
Therefore, the volume of the solid is (3π/5) units^3.
Learn more about quadrant here:
https://brainly.com/question/26426112
#SPJ11
PART II. MULTIPLE CHOISE. ( 18 marks)
Direction: Read the questions carefully and choose the correct option.( 2 marks each)
1. On January 2, Apple Company purchases factory machine at a cash price of $60,000. Related
expenditures are sales taxes $2,000, Insurance after the installation is $200, Installation and testing $1,000, Salvage value is $1,000. Useful life of the machine is 5 years.
a. Compute the cost component of the machine.
a.
$63,200
b.
$60,000
c.
$63,000
Answers
the correct answer is A. $63,200.
To compute the cost component of the machine, we need to add up all the related expenditures to the cash price of the machine.
Cash price of the machine: $60,000
Sales taxes: $2,000
Insurance after installation: $200
Installation and testing: $1,000
Total related expenditures: $2,000 + $200 + $1,000 = $3,200
Cost component of the machine: Cash price + Total related expenditures
Cost component of the machine = $60,000 + $3,200 = $63,200
Therefore, the correct answer is a. $63,200.
Learn more about Sales Taxes here :
https://brainly.com/question/29442509
#SPJ11
A fabric store sells two types of ribbon. One customer buys 3 rolls of the lace ribbon and 2 rolls of the satin ribbon and has a total of 120 yards of
ribbon. Another customer buys 2 rolls of the lace ribbon and 4 rolls of the satin ribbon and has a total of 160 yards of ribbon.
How many yards are on one roll of lace ribbon and one roll of satin ribbon?
OA. There are 10 yards on one roll of lace ribbon and there are 40 yards on one roll of satin ribbon.
OB. There are 20 yards on one roll of lace ribbon and there are 30 yards on one roll of satin ribbon.
OC. There are 30 yards on one roll of lace ribbon and there are 20 yards on one roll of satin ribbon.
OD. There are 40 yards on one roll of lace ribbon and there are 10 yards on one roll of satin ribbon.
Answers
Answer:
B
Step-by-step explanation:
3(20)=60
2(30)=60
60+60=120
2(20)= 40
4(30)= 120
40+120=160
Answer:
20 yards in the lace ribbon and there are 30 yards on one roll of satin ribbon
Step-by-step explanation:
3x + 2y = 120 (1)
2x + 4y = 160 (2)
Divide eq(2) by 2 (both sides). Keep equation (1) as is. You will get
3x + 2y = 120 (1')
x + 2y = 80 (2')
Now subtract eq(2') from eq(1'). You will get
2x = 120 - 80 = 40
x = 40/2 = 20.
Then from equation (2'),
20 + 2y = 80
2y = 80 - 20 = 60
y = 60/2 = 30
Q3. (1,1) are the coordinates of 2-dimensional Minkowski space and (T, X) are coordinates in a frame that is accelerating. They are related via t = ax sinh(aT) r = ax cosh(at) (i) Find the metric in the accelerating frame by transforming the metric of Minkowski space ds? = -dt? + dar to the coordinates (T, X). (You will need cosh²O - sinh? 0 = 1.) [4 Marks) (ii) Write down the geodesic Lagrangian in the (T, X) coordinates and identify a con- served quantity along geodesics. [4 Marks) (iii) From the condition L = -1 find an equation involving dX/dT for the geodesics. [4 Marks)
Answers
The conserved quantity along geodesics is d/dξ (ds/dξ)² = 0. The required metric is, ds² = - dt² + dx² = a²cosh²(at)(dT)² - a²sinh²(at)(dX)² = a²(T)² - (X)²
(1,1) are the coordinates of 2-dimensional Minkowski space and (T, X) are coordinates in a frame that is accelerating. They are related via t = ax sinh(aT) r = ax cosh(at)
(i) Finding the metric in the accelerating frame by transforming the metric of Minkowski space ds² = -dt² + dx² to the coordinates (T, X) is,
We have the transformation relation as,
t = ax sinh(aT)
r = ax cosh(aT)
The inverse transformation relations will be,
T = asinh(at)
x = acosh(at)
We will calculate the required metric using the inverse transformation.
The chain rule of differentiation is used to calculate the derivative with respect to t.
dt = aacosh(at)dX
dr = - aasinh(at)dt
So the required metric is,
ds² = - dt² + dx² = a²cosh²(at)(dT)² - a²sinh²(at)(dX)² = a²(T)² - (X)²
(ii) The geodesic Lagrangian in the (T, X) coordinates is given by,
L = ½ (ds/dξ)²,
where ds² = a²(T)² - (X)².
The conserved quantity along geodesics is d/dξ (ds/dξ)² = 0.
(iii) From the condition L = -1, we get,
-1 = ½ (ds/dξ)²,
which gives ds/dξ = i.
We have ds² = -dt² + dx² = - a²cosh²(at)(dT)² + a²sinh²(at)(dX)² = - a²(T)² + (X)².
Substituting ds/dξ = i in the above equation, we get dX/dT = ±i.
Learn more about Minkowski space visit:
brainly.com/question/31435333
#SPJ11
4x−3/2 - 5-2x/3 - 3x-4/3 = 5
Answers
Answer:
Simplify the expression.
2x-47
=6
Step-by-step explanation:
Answer:
x= -8.5
Step-by-step explanation:
combine like terms1/3x - 47/6 =5
2. Get x onone side
1/3x = -17/6
3. Multiply for x
x= -8.5
Find the length of the missing side and show the work please

Answers
Answer:
13 cm
Step-by-step explanation:
Using Pythagorean theorem
5²+12²=c²
25+144=c²
169=c²
In order to get rid of the ² it has to be square rooted
√169=√c²
c = 13
Please help me with this

Answers
Each tile has a surface area of 1 × 1 = 1 square foot since each tile is 1 foot long. As a result, the total mosaic's area is 49 x 1, or 49 square feet.
what is surface area ?The overall area that a three-dimensional object's surface occupies is known as surface area. Square units like square inches, square meters, and square feet are used to convey it. By adding up the areas of all the object's faces or surfaces, surface area is determined. By summing the areas of the cube's six faces, for instance, it is possible to get the surface area of a cube.
given
There are 7 rows and 7 tiles in the mosaic, making a total of 7 x 7 = 49 tiles in the mosaic.
Each tile has a surface area of 1 × 1 = 1 square foot since each tile is 1 foot long.
As a result, the total mosaic's area is 49 x 1, or 49 square feet.
To know more about surface area visit:
https://brainly.com/question/2835293
#SPJ1
The complete question is:- Mark's window store made a mosaic for the community center. The mosaic had a 7 x 7 array of different color square tiles. If each tile is 1ft long, what is the area of the whole mosaic?
which of the following does 6/7 x 3/5 equal?
18/32
18/35
18/33
Answers
Answer:18/35
Step-by-step explanation: 6*3 = 18
7*5 = 35
18 /35
Answer: 18/35
Step-by-step explanation:
6*3=18
7*5=35
18/35
Jacob ran 4 3/5 miles on Monday, 4.5 miles on Tuesday, and 3 3/5 miles on Wednesday. How many total miles did John run?
Answers
Answer:
12.7 or 12 7/10
Step-by-step explanation:
4 3/5 = 4.6 (decimal form)
3 3/5 = 3.6 (decimal form)
4.6 + 3.6 + 4.5 = 12.7
12.7 = 12 7/10 (as a fraction)
Have a great day!