1.
Write the equation of the line, in slope - intercept form, that goes through the point ( 12, 5 ) and is perpendicular to the line: y = - 6x - 14.
Answers
The equation of the line is y = 1/6x + 3
How to determine the equation?The equation of the line is given as:
y = -6x - 14
The above equation has a slope of
m = -6
Let the slope of the other line be n.
So, we have:
n =-1/m ---- slope condition for perpendicular lines
So, we have:
n = 1/6
The equation is then calculated as:
y = n(x - x1) + y1
Where
(x1, y1) = (12,5)
This gives
y = 1/6(x - 12) + 5
Expand
y = 1/6x - 2 + 5
Evaluate the sum
y = 1/6x + 3
Hence, the equation of the line is y = 1/6x + 3
Read more about linear equations at:
https://brainly.com/question/14323743
#SPJ1
Related Questions
10 - 4v = -2 - 4(-3 + v)
Answers
Answer:
All real numbers are solutions.
Step-by-step explanation:
Let's solve your equation step-by-step.
10−4v=−2−4(−3+v)
Step 1: Simplify both sides of the equation.
10−4v=−2−4(−3+v)
10+−4v=−2+(−4)(−3)+(−4)(v)(Distribute)
10+−4v=−2+12+−4v
−4v+10=(−4v)+(−2+12)(Combine Like Terms)
−4v+10=−4v+10
−4v+10=−4v+10
Step 2: Add 4v to both sides.
−4v+10+4v=−4v+10+4v
10=10
Step 3: Subtract 10 from both sides.
10−10=10−10
0=0

A bag contains 3 blue marbles, 10 green marbles, 4 yellow marbles, and 8 red marbles. A marble is chosen at random, not replaced, then another marble is chosen. What is the probability that it is a red marble, then a blue marble? Write your answer as a fraction in simplest form.
Answers
Answer:
There are a total of 25 marbles in the bag.
The probability of choosing a red marble first is 8/25 since there are 8 red marbles out of 25 marbles in the bag.
Since a marble is not replaced after the first selection, there are now 24 marbles in the bag. There are still 3 blue marbles in the bag.
The probability of choosing a blue marble second, after a red marble has already been selected, is 3/24 or 1/8 since there are 3 blue marbles left out of 24 marbles in the bag.
To find the probability of both events occurring together, we multiply their individual probabilities:
8/25 x 1/8 = 1/25
Therefore, the probability that a red marble is chosen first, followed by a blue marble, is 1/25.
A number of fiction books at a library was 3/4 of the total number of books. After 592 fiction books were donated to the library, the number of fiction books became 5/6 of the total number of books. How many books were there at th3 library at first?
Please, I become confused when 6ou say assume whatever as (x) or whatver
Answers
There approximately 7133 books in the library;
Data;
Let the number of total books = xNumber of fictional books = 3/4xWord ProblemTo solve this problem, we simply need to use an equation to explain the word problem into mathematical statements.
Let the total number of books be represented by x
The number of fictional books = 3/4x
After 592 fictional books were donated;
\(\frac{3x}{4} + 592 = \frac{5}{6}x\)
Let collect like terms and solve
\(\frac{3x}{4} +592 = \frac{5}{6} x\\\frac{5}{6}x - \frac{3x}{4} = 592\\ 0.083x=592\\x = 592/0.083\\x = 7132.53\)
There approximately 7133 books in the library;
Learn more on word problems here;
https://brainly.com/question/13818690
In circle Qwith the measure of minor arc PR= 70°, find m/PSR.
Answers
Answer: 290 degrees
Step-by-step explanation:
subtract the minor arc's measure from 360 to get the major arc's measure
PLEASE HELP FAST!!
Determine the number of solutions to the system of linear equations shown on the graph.
A: No solution
B: Infinitely many solutions
C: One solution at (-3,2)
D:One solution at (2,-3)

Answers
Answer:
the answer is D
both lines intersect at (2, -3)
hope this helps <3
Is this function linear?

Answers
which expression is equivalent to 2^3/2^7
A. 2^4
B. 1/2^4
C. -2^4
D. - 1/2^4
Answers
26. Tyler has been saving his winning lottery tickets. He has 23 tickets that are worth a total of $175. If each ticket is worth either $5 or $10, how many of each does he have?
Answers
If triangle ABC is reflected across the line y = x, are the pre-image and image congruent? Why, or why not?
OYes, distance and angle measure are preserved
OYes, angle measure is preserved and distance is not
O No, distance is preserved but angle measure is not
O No, neither distance nor angle measure are preserved
Answers
The correct answer is: O Yes, distance and angle measure are preserved.
When a triangle ABC is reflected across the line y = x, the pre-image and image are congruent.
This is because the line y = x is the perpendicular bisector of the segment joining each corresponding point of the pre-image and image.
Reflection across the line y = x is a type of transformation known as an isometry, which preserves both distance and angle measure.
Here's why:
Distance preservation:
When a point is reflected across the line y = x, the distance between the original point and its reflection remains the same.
This holds true for all corresponding points of the triangle.
Therefore, the distance between any two corresponding points in the pre-image and image triangle will be equal, resulting in distance preservation.
Angle preservation: When a line segment is reflected across the line y = x, the angle between the line segment and the line y = x is preserved. This means that the corresponding angles in the pre-image and image triangle will be congruent.
Since both distance and angle measure are preserved during reflection across the line y = x, the pre-image and image triangles are congruent.
It's important to note that congruence under reflection across a line holds only when the line of reflection is the same for both the pre-image and image.
If the line of reflection were different, the triangles would not be congruent.
For similar question on distance.
https://brainly.com/question/26550516
#SPJ8
Subtract 3 1/4-2 1/3
Answers
Answer:11/12
Step-by-step explanation:
3 1/4=13/4. Change to improper
2 1/3=7/3^^^
13/4-7/3=? new equation
4*3=12, find the common denominator(if you're lazy just multiply the denominators with each other) but now you have to do the same with the numerator
13*3(because we multiplied 4 BY 3 in the first equation)
7*4(again because for this one we multiplied 3 BY 4)
39/12-28/12=11/12
The first number in a pattern is 138, and the rule is to add 15. What is the next number in the pattern?
Answers
g(t)=−(t−1)
2
+5g, left parenthesis, t, right parenthesis, equals, minus, left parenthesis, t, minus, 1, right parenthesis, squared, plus, 5
What is the average rate of change of
�
gg over the interval
−
4
≤
�
≤
5
−4≤t≤5minus, 4, is less than or equal to, t, is less than or equal to, 5?
Answers
The average rate of change over is 1.
Given that;
the function is,
⇒ g (t) = - (t - 1)² + 5
Hence, We need to determine the average rate of change over the interval - 4 ≤ t ≤ 5.
The value of G(-4):
The value of G(-4) can be determined by substituting t = -4 in the function
⇒ g (t) = - (t - 1)² + 5
Thus, we have,
⇒ g (t) = - (-4 - 1)² + 5
⇒ g (t) = - 20
Thus, the value of G(-4) = -20
The value of G(5):
The value of G(5) can be determined by substituting t = 5 in the function , we get,
⇒ g (t) = - (t - 1)² + 5
⇒ g (t) = - (5 - 1)² + 5
⇒ g (t) = - 11
Thus, the value of G(5) is, -11
Now, Average rate of change:
The average rate of change can be determined using the formula,
⇒ G(b) - G (a) / (b - a)
where, a = - 4 and b = 5
Substituting the values, we get,
⇒ G(5) - G (-4) / (5 - (-4))
⇒ ( - 11 - (- 20)) / 9
⇒ 9/9
⇒ 1
Thus, the average rate of change over the interval is. 1.
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ1
Please help much appreciated!!!!!!!!!!!!!

Answers
Answer:
The triangle is an isosceles triangle
Step-by-step explanation:
Let's get some definitions out of the way:
A scalene triangle is a triangle in which all three sides are in different lengths, and all three angles are of different measures.
An isosceles triangle is a triangle in which two sides are equal lengths, and angles opposite to equal sides are equal
An equilateral triangle is a triangle in which all three sides are equal and all three angles are equal
Let's determine the lengths of each of the three sides in ΔXYZ
The distance formula for the distance between any two points (x1, y1) and (x2, y2) is given by
d² = (x2 - x1)² + (y2 - y1)²
So the distance = the square root of the above expression - d
To find length of XY, take points X(4, 2) and Y(2, -2)
Length XY
\(\sqrt{4-2)^2 + (2 - (-2)^2}\\\\= \sqrt {{4} + {16}}\\\\= \sqrt{20}\)
Length YZ with Y(2, -2) and Z(-2, 0):
\(= \sqrt {(-2 - 2)^2 + (0 - (-2))^2}\\\\ = \sqrt {(-4)^2 + (2)^2}\\\\ = \sqrt {{16} + {4}}\\\\= \sqrt{20}\)
length XZ with X(4, 2) and Z(-2, 0):
\(= \sqrt {(-2 - 4)^2 + (0 - 2)^2}\\\\= \sqrt {(-6)^2 + (-2)^2}\\\\= \sqrt {{36} + {4}}\\\\= \sqrt {40}\)
So in triangle XYZ we have two sides equal.
These are XY and YZ
The third side is different
So the triangle is an isosceles triangle
-5v + 6 = 26 solve for v
Answers
Answer:v=-4
Step-by-step explanation:We move all terms to the left:
-5v+6-(26)=0
We add all the numbers together, and all the variables
-5v-20=0
We move all terms containing v to the left, all other terms to the right
-5v=20
v=20/-5
what value of X makes the model true?

Answers
The value of x is -1 which makes the model true
The equation from the given model will be 5x+6=1
We have to find the value of x
5x+6=1
Subtract 6 from both sides
5x=-5
Divide both sides by 5
x=-1
Hence, the value of x is -1 which makes the model true
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
A rectangle has an area of 114cm squared and a perimeter of 50cm. What are the dimensions
Answers
If rectangle has an area of 114cm squared and a perimeter of 50 cm, the dimensions of the rectangle are approximately 5 cm by 22.8 cm.
Let's assume the length of the rectangle is "l" and the width is "w". We can start by using the formula for the area of a rectangle, which is A = lw. From the given information, we know that the area is 114cm².
So, we have:
lw = 114
Next, we can use the formula for the perimeter of a rectangle, which is P = 2l + 2w. From the given information, we know that the perimeter is 50cm.
So, we have:
2l + 2w = 50
We now have two equations with two variables, which we can solve using substitution or elimination. Let's use substitution by solving the first equation for l:
l = 114/w
We can then substitute this expression for l in the second equation:
2(114/w) + 2w = 50
Multiplying both sides by w to eliminate the fraction, we get:
228 + 2w² = 50w
Rearranging and simplifying, we get a quadratic equation:
2w² - 50w + 228 = 0
We can solve for w using the quadratic formula:
w = [50 ± √(50² - 4(2)(228))]/(2(2)) ≈ 11.4 or 5
Since the length and width must be positive, we can discard the solution w = 11.4. Therefore, the width of the rectangle is approximately 5 cm. We can then use the equation lw = 114 to solve for the length:
l(5) = 114
l ≈ 22.8
To learn more about rectangle click on,
https://brainly.com/question/19127628
#SPJ1
Fill in the table 'using this function rule.
y = -5x+2
x
-1
0
1
2
y
0
0
0
X
4
S

Answers
Answer:
7, 2, -3, -8
Step-by-step explanation:
y = -5x + 2 Substitute in -1 for x
y = -5(-1) + 2
y = 5 + 2
y = 7
y = -5x + 2 Substitute in 0 for x
y = -5(0) + 2
y = 0 + 2
y = 2
y = -5 + 2 substitutes in 1 for x
y = -5(1) + 2
y = -5 + 2
y = -3
y = -5x + 2 Substitute in 2 for x
y = -5(2) + 2
y = -10 + 2
y = -8
Helping in the name of Jesus.
8 ft 10 ft Find the area of this figure. Round your answer to the nearest hundredth. Use 3.14 to approximate . A = [?]ft? Notice that only half of the circle is included in the figure!

Answers
find the area of the rectangle;
w x l = 8 x 10 = 80ft^2
circle;
pi(r)^2
r = 4
pi(4)^2
pi(16) = 50.24
80 + 50.24 = 130.24
4. Chelsea determined that the value of x in the triangle at the right was 5.
a. Find the value of each angle by substituting 5 for x.
b. Was Chelsea's solution, x = 5, correct? How do you know?
15x
x
11x
(8x+5)
Z

Answers
Step-by-step explanation:
a) 11*5=55
15*5=75
8*5+5=45
b) No, because (55+75+45=175°) and the perimeter of a triangle is 180°

What is the total cost of 2.3 cubic meters of soil if it sells for $45 per cubic meter?
The total cost is $
(Type an integer or a decimal.)

Answers
Find total cost
1 cubic meter:45$
2.3 cubic meter: 45 x 2.3 = 103.5$
So the total cost is 103.5$
Two-fifths of one less than a number is less than three-fifths of one more than that number. What numbers are in the solution set of this problem
A.x<-5
B.x>-5
C.x>-1
D.x<-1
Answers
Answer:
B. x > -5
Step-by-step explanation:
It seems you have a number x such that ...
\(\dfrac{2}{5}(x-1)<\dfrac{3}{5}(x+1)\\\\2x-2<3x+3\qquad\text{multiply by 5, eliminate parentheses}\\\\-5<x\qquad\text{subtract $2x+3$}\)
This matches choice B: x > -5.
What is mZDFE?
E
m2DFE =
74⁰
G
LL
D

Answers
The measure of angle DEF is 37 degrees.
What is chord in circle
In geometry, a chord is a straight line segment that connects two points on the circumference of a circle. More specifically, a chord of a circle is a line segment whose endpoints lie on the circle.
Every circle has infinitely many chords, but some of the most commonly discussed chords are the diameter (a chord that passes through the center of the circle), and the secant (a chord that intersects the circle at two distinct points).
Chords play an important role in geometry, as they can be used to determine various properties of circles, such as their radius, diameter, and area.
Since G is the center of the circle, the angle DGE is a central angle of the circle.
Therefore, the angle DGE is equal to twice the inscribed angle DEF that subtends the same arc DE.
Let x be the measure of angle DEF. Then, we have:
2x = 74
x = 37
Hence, the measure of angle DEF is 37 degrees.
To know more about circle visit :-
https://brainly.com/question/24375372
#SPJ1
David has 55% ownership of a company. If there are 1,300,000 stocks, how many stocks
loes he own?
Answers
Answer:
715000
Step-by-step explanation:
1300000 • 55%,
55% = 0.55
1300000 • 0.55 = 715000
G(n) = n^2 +4n find g(2)
Answers
Answer:
12
Step-by-step explanation:
G(2)= 2^2 +4(2)
Solve via order of operations
G(2)=4 +8
G(2)=12
Bob the builder eat no fewer then three donuts. What is the inequality?
Answers
Answer:
3
Step-by-step explanation:
I think
Answer:
less than or equal to 3
Step-by-step explanation:
pls hurry ill make brainliest!
The tape diagram represents an equation.
20
9
9
Write an equation to represent the tape diagram.
Choose 1 answer:
А
20 = 9:2
B
20 = 2g
Find the value of g that makes the equation true.
9
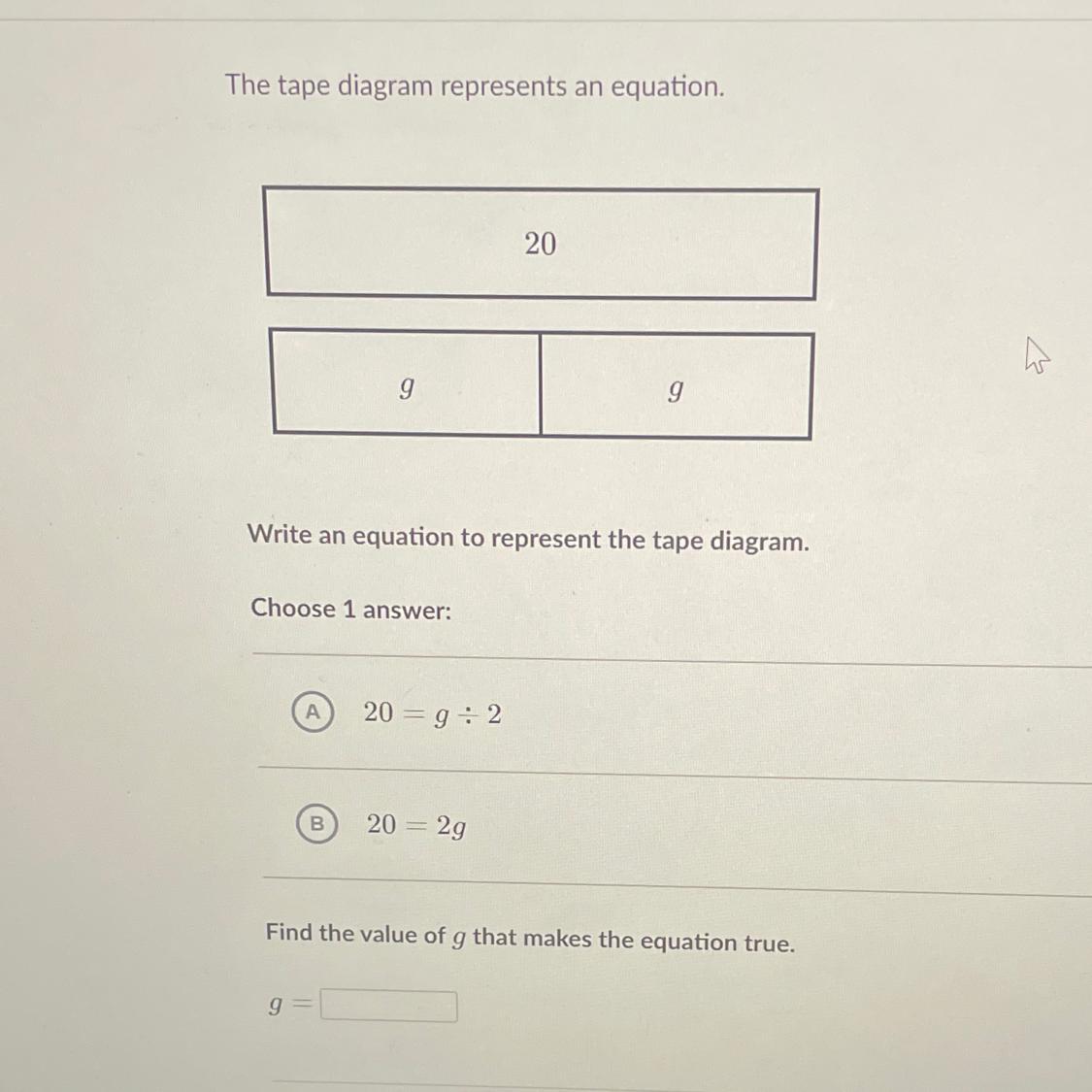
Answers
Answer:
B.
g= 10
Step-by-step explanation:
Calculate the distance between the points C = (0,-2) and L= (-4, 1) in the coordinate plane. Give an exact answer. (not a decimal approximation)
Answers
Answer: 5
Step-by-step explanation:
\(\sqrt{(-4-0)^2 + (1-(-2))^2}=5\)

Suppose that you take 300 mg of an antibiotic every 6 hr. The half-life of the drug is 6 hr (the time it takes for half of the drug to be eliminated from your blood). Use infinite series to find the long-term (steady state) amount of antibiotic in your blood exactly.
Answers
Answer:
1200000
Step-by-step explanation:
Esun as ma
The half-life of Radium-226 is 1590 years. If a sample contains 400 mg, how many mg will remain after 1000
years?
Answers
Answer:
258.65 mg will be remain after 1000 years
Step-by-step explanation:
This problem can be solved several ways, I prefer the natural log approach for reasons I won’t go into here:
Activity final = Activity initial e^-kt, where
k = the decay constant, = ln2/half life = 0.693/1590, = 0.000436/year
t = the decay time, in the same time base as k
The problem can be worked in units of activity, mass, or number of atoms.
400 x e^-0.000436 x 1000 = 400 x e^-.436 = 258.65 mg
you can check this by estimating. There is about 2/3 of a half life, so there should be more than 200 mg, which would be the value at one half life.
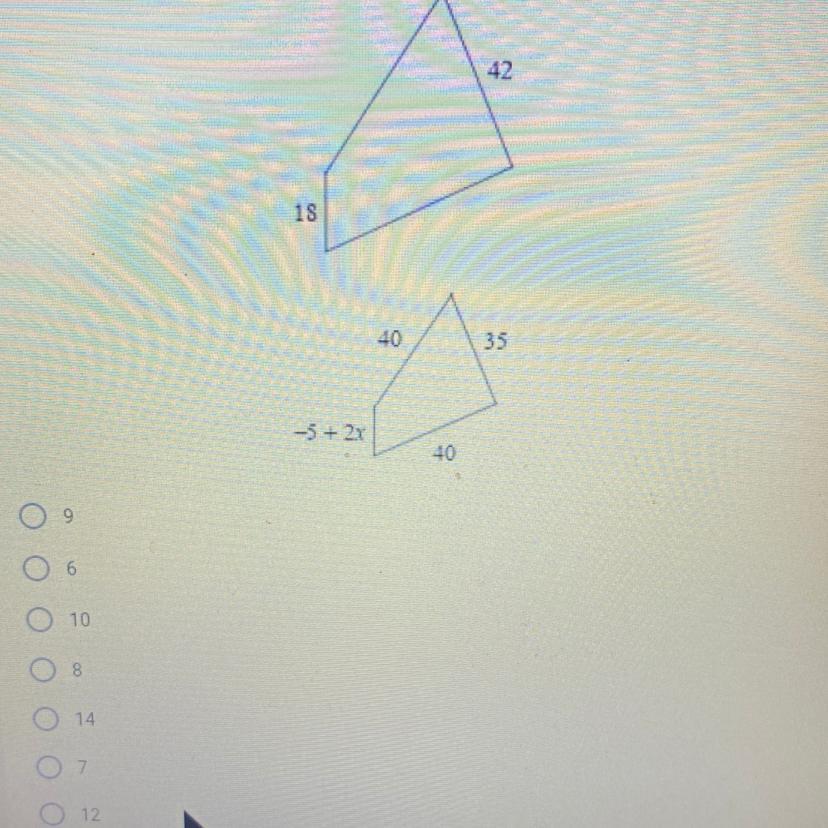
⚠️NEED HELP ASAP ⚠️The following polygons are similar. Solve for x.