(1/a*b-b^2)+(1/a*b-a^2)
Answers
Simplified version of this expression \((1/ab-b^2) + (1/ab-a^2)\)is\([(2 - a^2 - ab^2)/(ab)]\)
To simplify the expression \((1/ab-b^2) + (1/ab-a^2)\), let's break it down step by step.
First, let's focus on the first term,\((1/ab-b^2)\). To combine the terms, we need to find a common denominator. The denominator for the first term is ab. Therefore, we need to rewrite the expression with the common denominator:
\([(1 - ab^2)/(ab)]\)
Next, let's simplify the second term,\((1/ab-a^2)\). Again, we need a common denominator, which is ab. So we rewrite the expression:
\([(1 - a^2)/(a*b)]\)
Now, we can combine the two terms by adding their numerators:
\([(1 - ab^2 + 1 - a^2)/(ab)]\)
Simplifying further, we have:
\([(2 - a^2 - ab^2)/(ab)]\)
At this point, we cannot simplify the expression any further since there are no common factors or like terms in the numerator and denominator.
In conclusion, the simplified expression\((1/ab-b^2) + (1/ab-a^2)\) is\([(2 - a^2 - ab^2)/(ab)]\). This expression represents the result obtained after combining the terms, finding a common denominator, and simplifying the numerator. It is important to note that the simplicity of the expression depends on the specific values of 'a' and 'b' in the context of the problem.
For more such information on: expression
https://brainly.com/question/1859113
#SPJ8
Related Questions
if i have an 3-digit number times an 3-digit number, and the product of the leading digits is 10 or more, then the answer to this multiplication problem will have how many digits?
Answers
The product of the leading digits is 10 or more, then the answer to this multiplication problem will have Seven digits.
The product of two numbers is the answer when they are multiplied. So, the product of 5 and 4 is the multiplication 5× 4 and is equal to 20.
A 3-digit number times an 3-digit number.
The largest 3-digit number = 999
The product of largest 3 digit number and 3 digit number = 999×999
= (1000-1)(1000-1)
=( 1000)² - 2000 + 1
= 1000000 - 1999
= 998001
Which is 6-digit number. So, the product of three digit number with three digit number is cannot be greater than 6-digit number .
Now, the product of 3-digit number times an 3-digit number is multiply by 10 then one more digit added to it .
So, the possible answer of this multiplication problem consists 7-digit number.
To learn more about 3-digit number , refer:
https://brainly.com/question/713808
#SPJ4
The number of blueberry muffins Gary bakes each day is 30% of the total number of muffins he bakes. If he baked 24 blueberry muffins on Sunday, what is the total number of muffins baked?
Answers
Answer: The answer is 80
Step-by-step explanation:
Answer:
Gary baked 80 muffins on Sunday
Step-by-step explanation:
I can set up a proportion, knowing that 24/x = 3/10, where x is the total number of muffins baked on Sunday. By cross multiplying, I get 240 = 3x. By dividing both sides by 3, I find x = 80.
can anybody help me with this problem in math ? asap .

Answers
Answer:
c. y = 1/2x - 2
Step-by-step explanation:
they have the same gradient so are parallel
i’m not sure what the last one is .. can u help pls

Answers
Answer:
136
Step-by-step explanation:
180 - <BAC
May I have help on this please? thanks if you do!
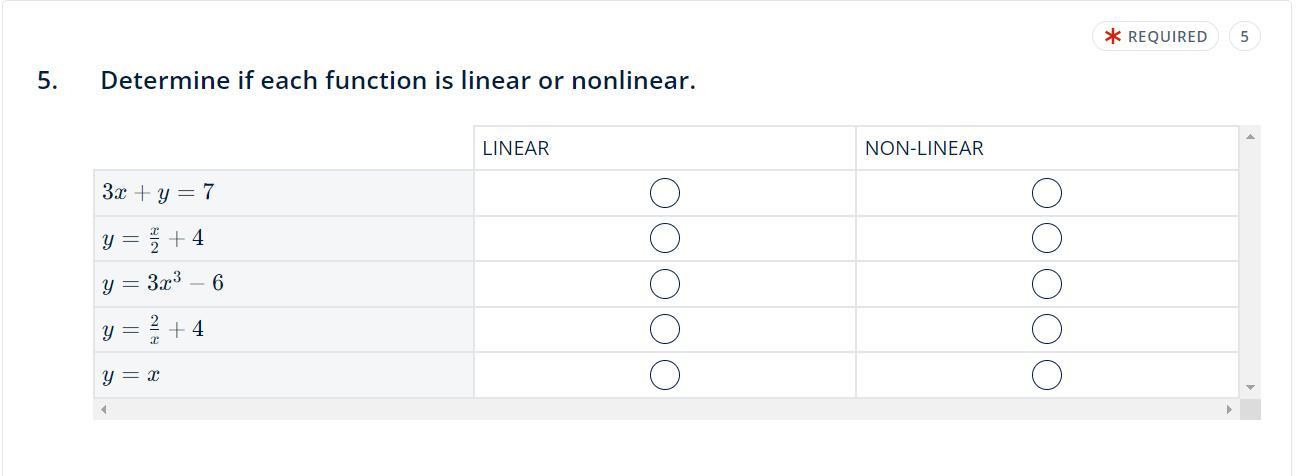
Answers
Answer: 1. linear equation
2. non-linear equation
3. non-linear equation
4. non-linear equation
5. linear equation
Step-by-step explanation:
not sure
∆GET ≅ ∆ABS. AB= 10, BS=13, AS=18, and GT=4x-8, what is the value of 'x'?
Answers
The value of x for GT is 6.5 .
What is the congruence of triangles?
If all three corresponding sides and all three corresponding angles are equal in size, two triangles are said to be congruent. Slide, twist, flip, and turn these triangles to create an identical appearance. They are in alignment with one another when moved.
Given, ΔGET ≅ ΔABS
Following the statement that corresponding sides of congruent triangles are congruent, we have:
GE = AB, ET = BS and GT = AS -(i)
AB = 10, BS = 13, AS = 18, GT = 4x - 8 -(ii)
Comparing (i) and (ii) we have, 4x - 8 = 18 ⇒ 4x = 26 ⇒ x = 26/4 = 6.5
Thus, the value of x for GT is 6.5 .
To learn more about this, tap on the link below:
https://brainly.com/question/3999145
#SPJ9
can someone help please

Answers
When Tracey pours all the water from the smaller 5-inch cube container into the larger 7-inch cube container, the water will be approximately 7 inches deep in the larger container.
To find out how deep the water will be in the larger container, we need to consider the volume of water transferred from the smaller container. Since both containers are cube-shaped, the volume of each container is equal to the length of one side cubed.
The volume of the smaller container is 5 inches * 5 inches * 5 inches = 125 cubic inches.
When Tracey pours all the water from the smaller container into the larger container, the water completely fills the larger container. The volume of the larger container is 7 inches * 7 inches * 7 inches = 343 cubic inches.
Since the water fills the larger container completely, the depth of the water in the larger container will be equal to the height of the larger container. Since all sides of the larger container have the same length, the height of the larger container is 7 inches.
Therefore, the water will be approximately 7 inches deep in the larger container.
For more such questions on container
https://brainly.com/question/29398973
#SPJ8
determine whether the systems have one solution, no solution, or infinitely many solutions
3x-2y=3;6x-4y=1
3x-5y=8;5x-3y=2
3x 2y=8;4x 3y=1
3x-6y=3;2x-4y=2
3x-4y=2;6x-8y=1
Answers
Answer:
First system: no solution
Second system: one solution
Third system: one solution
Fourth system: infinite solutions
Fifth system: no solution
Step-by-step explanation:
First system: 3x-2y=3; 6x-4y=1
From the first equation: y = (3x - 3)/2
Using this value of y in the second equation:
6x - 6x + 6 = 1
6 = 1 -> System has no solution
Second system: 3x-5y=8; 5x-3y=2
From the first equation: x = (8 + 5y)/3
Using this value of x in the second equation:
5*(8 + 5y) - 9y = 6
40 + 25y - 9y = 6
16y = -34 -> y = -2.125
x = (8 - 5*2.125)/3 = -0.875
This system has one solution
Third system: 3x-2y=8; 4x-3y=1
From the first equation: x = (8 + 2y)/3
Using this value of x in the second equation:
4*(8 + 2y) - 9y = 3
32 + 8y - 9y = 6
y = 26
x = (8 + 2*26)/3 = 20
This system has one solution
Fourth system: 3x-6y=3; 2x-4y=2
From the first equation: x = 1 + 2y
Using this value of x in the second equation:
2*(1 + 2y) - 4y = 2
2 + 4y - 4y = 2
2 = 2
This system has infinite solutions
Fifth system: 3x-4y=2; 6x-8y=1
From the first equation: x = (2 + 4y)/3
Using this value of x in the second equation:
2*(2 + 4y) - 8y = 1
4 + 8y - 8y = 2
4 = 2
This system has no solution
I need help lol xoxoxo

Answers
Convert the integral below to polar coordinates and evaluate the integral. ∫ 0
5/ 2
∫ y
25−y 2
xydxdy Instructions: Please enter the integrand in the first answer box, typing theta for θ. Depending on the order integration you choose, enter dr and order into the second and third answer boxes with only one dr or dtheta in each box. Then, enter the limits of integration and evaluate the integral to find the volume. ∫ A
B
∫ C
D
□□ A= B= C=
D=
Volume = Consider the solid shaped like an ice cream cone that is bounded by the functions z= x 2
+y 2
and z= 50−x 2
−y 2
. Set up an integral in polar coordinates to find the volume of this ice cream cone. Instructions: Please enter the integrand in the first answer box, typing theta for θ. Depending on the order of integration you choose, enter dr and dtheta in eithe order into the second and third answer boxes with only one dr or dtheta in each box. Then, enter the limits of integration and evaluate the integral to find the volume. ∫ A
B
∫ C
D
□
Answers
The polar form is \(r^2\)cosθsinθ dr dθ and A = 0, B = 5, C = 0, D = π/2. The volume enclosed by the given region is 125/6 cubic units.
To convert the given integral to polar coordinates, we need to express the variables x and y in terms of r and θ. In polar coordinates, x = rcosθ and y = rsinθ. Let's proceed with the conversion.
The integrand xy can be expressed as (rcosθ)(rsinθ) = \(r^2\)cosθsinθ.
The limits of integration need to be determined as well. The integral is given as ∫ 0 to 5/√2 ∫ y to √(25 - \(y^2\)) \(r^2\)cosθsinθ dx dy.
To determine the limits, let's first consider the bounds of y. The lower limit of y is given as y = 0, and the upper limit of y is √(25 - \(y^2\)). We can rewrite this equation as \(y^2\) + \(x^{2}\) = 25, which represents a circle with a radius of 5 centered at the origin. The upper limit of y corresponds to the upper semicircle of the circle.
In polar coordinates, the equation of this upper semicircle is r = 5. Therefore, the limits of integration for r are from 0 to 5.
For the angle θ, the integral is taken over the region from y to √(25 - \(y^2\)). In polar coordinates, this corresponds to the angle from the positive x-axis to the line connecting the origin to the point (x, y) on the upper semicircle. This angle can be expressed as θ = 0 to π/2.
Now, let's write the integral in polar coordinates and evaluate it:
∫ A to B ∫ C to D \(r^2\)cosθsinθ dr dθ =
A = 0 (lower limit of r)
B = 5 (upper limit of r)
C = 0 (lower limit of θ)
D = π/2 (upper limit of θ)
Now, let's evaluate the integral:
∫ 0 to 5 ∫ 0 to π/2 \(r^2\)cosθsinθ dr dθ
Integrating with respect to r first:
∫ 0 to π/2 [(1/3)\(r^3\)cosθsinθ] from 0 to 5 dθ
= (1/3) ∫ 0 to π/2 (\(5^3\)cosθsinθ) dθ
= (1/3) (125) ∫ 0 to π/2 cosθsinθ dθ
Now, integrating with respect to θ:
= (1/3) (125) [(-1/2)\(cos^2\)θ] from 0 to π/2
= (1/3) (125) [(-1/2)(\(0^2\) - \(1^2\))]
= (1/3) (125) (1/2)
= 125/6
Therefore, the volume enclosed by the given region is 125/6 cubic units.
Correct Question :
Convert the integral below to polar coordinates and evaluate the integral. ∫ 0 to 5/ 2∫ y to √(25 - \(y^2\)) xy dx dy
Instructions: Please enter the integrand in the first answer box, typing theta for θ. Depending on the order integration you choose, enter dr and order into the second and third answer boxes with only one dr or dtheta in each box. Then, enter the limits of integration and evaluate the integral to find the volume.
∫A to B ∫C to D =
A=
B=
C=
D=
To learn more about volume here:
https://brainly.com/question/32532372
#SPJ4
A flagpole is 15 feet tall. Its shadow is 20 feet long. How far is it from the top of the flagpole to the end of the shadow?
Answers
Answer:
5 feet.
Step-by-step explanation:
The angle of the height and length go down to 5 feet diagonally.
Answer:
25ft
Step-by-step explanation:
To find the length of the top of the flagpole to the end of the shadow, you have to use the Pythagorean theorem a² + b² =c²
15² + 20² = x²
225 + 400 = x²
625 = x²
√625 = √x²
x = 25
someone please help me, thank you

Answers
What is an equation example?
Answers
The definition and explanation of an equation are given below with an example.
in mathematics, an equation is defined as an expression that expresses equality between 2 quantities or expressions. We use equations quite a lot in our daily lives whenever we have to equate two quantities and find out how they are equal. These are used in all branches of science because of the huge purpose they serve.
in simple words it tells what we have on the Left-Hand Side of the "=" sign is the same as what we have on the right-hand side of the statement. Some examples of equations are-
E²=m²c⁴+p²c²
x²+3x-1=0
70 oranges= 7 oranges × 10 oranges
Learn more about equations on
https://brainly.com/question/29657983?referrer=searchResults
#SPJ4
Determine an appropriate interval width for a random sample of 180 observations that fall between and include the values below. a. 20 to 65 b. 30 to 150 c. 40 to 290 d. 100 to 700 a. What is an appropriate interval width? \begin{tabular}{ll} 1 \\ 9 & 5 \\ \hline 3 \end{tabular}
Answers
An appropriate interval width for the given range of values is 30.
To determine an appropriate interval width for a given range of values, you need to consider the desired level of precision and the number of intervals you want to create.
One commonly used method to determine the interval width is to use the range of the data divided by the desired number of intervals. However, in the absence of information about the desired number of intervals, we can still calculate the interval width using the given range of values.
Let's calculate the interval width for each case:
a. For the range 20 to 65:
Interval width = (Max value - Min value) / Number of intervals
The given range is 20 to 65, so the maximum value is 65 and the minimum value is 20. Since the number of intervals is not specified, we can choose a reasonable value. Let's use 10 intervals as an example.
Interval width = (65 - 20) / 10 = 45 / 10 = 4.5
Therefore, an appropriate interval width for the given range of values is approximately 4.5.
b. For the range 30 to 150:
Using the same method as above, we can calculate the interval width:
Interval width = (150 - 30) / Number of intervals
Again, the number of intervals is not specified. Let's use 12 intervals as an example.
Interval width = (150 - 30) / 12 = 120 / 12 = 10
Therefore, an appropriate interval width for the given range of values is 10.
c. For the range 40 to 290:
Similarly, we can calculate the interval width:
Interval width = (290 - 40) / Number of intervals
Assuming 15 intervals for this example:
Interval width = (290 - 40) / 15 = 250 / 15 = 16.67 (approximately)
Hence, an appropriate interval width for the given range of values is approximately 16.67.
d. For the range 100 to 700:
Following the same approach:
Interval width = (700 - 100) / Number of intervals
Taking 20 intervals as an example:
Interval width = (700 - 100) / 20 = 600 / 20 = 30
Therefore, an appropriate interval width for the given range of values is 30.
To know more about interval, visit:
https://brainly.com/question/11051767
#SPJ11
a student applies for ten different scholarships to various universities. seven of the scholarships pay for books. four scholarships include a meal ticket. two of the scholarships exclude meals and books. how many scholarships pay for both books and meals? use a venn diagram to illustrate and help solve this problem
Answers
The number of scholarships that pay for both books and meals is 1.
To solve this problem, we need to use the concept of set intersection. Let B be the set of scholarships that pay for books, and M be the set of scholarships that include a meal ticket. We want to find the number of scholarships that pay for both books and meals, which is the size of the set intersection B ∩ M.
From the problem statement, we know that:
|B| = 7 (seven scholarships pay for books)
|M| = 4 (four scholarships include a meal ticket)
We can use the inclusion-exclusion principle to find |B ∩ M|:
|B ∩ M| = |B| + |M| - |B U M|
We need to find the size of the union of the sets B and M, which includes all scholarships that pay for books, all scholarships that include a meal ticket, and possibly some scholarships that pay for both. From the problem statement, we know that there are two scholarships that exclude both meals and books, so we can subtract that from the union:
|B U M| = |B| + |M| - |B ∩ M| + 2
Substituting the known values, we get:
|B ∩ M| = |B| + |M| - |B U M| + 2
|B ∩ M| = 7 + 4 - (7 + 4 - |B ∩ M| + 2) + 2
|B ∩ M| = 1 + |B ∩ M|
Solving for |B ∩ M|, we get
|B ∩ M| = 1
Learn more about inclusion-exclusion principle here
brainly.com/question/27975057
#SPJ4
The given question is incomplete, the complete question is:
A student applies for ten different scholarships to various universities. seven of the scholarships pay for books. four scholarships include a meal ticket. two of the scholarships exclude meals and books. how many scholarships pay for both books and meals?
Determine the values of r for which the differential equation t²y" — 6ty' + 6y = 0 has solutions of the form y = tº for t > 0. Number of values of r Choose one ▼
Answers
The differential equation t^2y" - 6ty' + 6y = 0 has solutions of the form y = t^r for t > 0 when r = 1 and r = 6.
There are two values of r.To find the values of r for which the differential equation t^2y" - 6ty' + 6y = 0 has solutions of the form y = t^r for t > 0, we can substitute y = t^r into the differential equation and solve for r.
Let's substitute y = t^r into the equation:
t^2y" - 6ty' + 6y = 0
Differentiating y = t^r with respect to t:
y' = rt^(r-1)
y" = r(r-1)t^(r-2)
Substituting these derivatives into the differential equation:
t^2(r(r-1)t^(r-2)) - 6t(rt^(r-1)) + 6(t^r) = 0
Simplifying:
r(r-1)t^r - 6rt^r + 6t^r = 0
Factor out t^r:
t^r (r(r-1) - 6r + 6) = 0
For a non-trivial solution, t^r cannot be zero, so we must have:
r(r-1) - 6r + 6 = 0
Expanding and rearranging:
r^2 - r - 6r + 6 = 0
r^2 - 7r + 6 = 0
Now we can factor the quadratic equation:
(r - 1)(r - 6) = 0
This gives us two possible values for r:
r - 1 = 0 => r = 1
r - 6 = 0 => r = 6
Therefore, the differential equation t^2y" - 6ty' + 6y = 0 has solutions of the form y = t^r for t > 0 when r = 1 and r = 6. There are two values of r.
Learn more about derivatives here: brainly.com/question/25324584
#SPJ11
what is an equivalent ratio to 100:200
Answers
Answer:
Original Ratio: 100:200
Divide both sides by 100: 1:2
The ratio 1:2 cannot be simplified further, so 1:2 is he correct answer.
Let me know if this helps!
Discuss concisely why turbulence modelling, which is the construction and use of a mathematical model to predict the effects of turbulence, are needed and employed in CFD simulations. Use bullet points in writing down your answers.
Answers
Turbulence modeling is needed and employed in Computational Fluid Dynamics (CFD) simulations because turbulence is characterized by chaotic and unpredictable fluid motion.
Turbulence models are mathematical models that are constructed and used to predict the effects of turbulence on fluid flow.
- Turbulence modeling helps to improve the accuracy and reliability of CFD simulations by predicting the behavior of fluid flow under turbulent conditions.
- Turbulence modeling helps to reduce the computational cost of CFD simulations by approximating the effects of turbulence on fluid flow.
- Turbulence modeling allows for the analysis of complex fluid flow problems that would be difficult or impossible to solve analytically.
- Turbulence modeling provides insight into the physics of fluid flow under turbulent conditions, which can lead to improvements in design and optimization of engineering systems.
Turbulence modeling is an essential component of CFD simulations because it allows for the efficient and accurate prediction of fluid flow under turbulent conditions. the effects of turbulence, engineers can analyze complex fluid flow problems and optimize engineering systems.
To know more about Turbulence visit:-
https://brainly.com/question/11443433
#SPJ11
You are traveling long distance for the first time in your new car. If the polynomial 90d² + 30d
represents the miles traveled and you have traveled for 15d hours, find the average speed in the
simplest form.
8d miles per hour
O 6d² + 2d miles per hour
6d+ 2 miles per hour
O6d² + 2 miles per hour

Answers
Therefore, the average speed in the simplest form is 6d² + 2d miles per hour.
What is expression?In mathematics, an expression is a combination of symbols and values that can be evaluated to obtain a result. Expressions can contain variables, constants, operators, and functions, which can be combined using arithmetic or algebraic operations to form more complex expressions. Examples of expressions include 2 + 3, x + 5, and sin(θ) + cos(θ).
Here,
The given polynomial 90d² + 30d represents the miles traveled. We can find the average speed by dividing the distance traveled by the time taken. Since we have traveled for 15d hours, the total distance traveled is (90d² + 30d) miles. Thus, the average speed is:
=(90d² + 30d) miles / (15d) hours
= 6d² + 2d miles per hour
To know more about expression,
https://brainly.com/question/1859113
#SPJ1
How is a rate simile do different from a ratio?
Answers
Amir is starting a stamp collection. After 3 weeks he has collected 35 different stamps, and after 9 weeks he has collected 105 different stamps. What is the constant of proportionality in this direct variation?
Answers
Answer:
3/35
Step-by-step explanation:
Here, we want to know the constant of proportionality in this direct variation scenario
Since it is a direct variation, the form we are having would be;
x = ky
where x and y directly vary with each other and k is the constant of proportionality
Now, for the first relation
3 = 35k
for the second
9 = 105k
Thus k would be
3/35 which is the same as 9/105
Kindly note that 9/105 can be reduced to 3/35
So linking the number of weeks to the number of stamps collected, the constant of proportionality is 3/35
The answer is A.) y =35/3x

The measure of angle R is 65 degrees. Fond the measure of angle S.

Answers
Answer:
50
Step-by-step explanation:
If R is 65, then T must also be 65 because both of the sides are congruent. 65+65=130 and all angles on a triangle add to 180. Therefore 180-130 is 50
Which pair of quantities is LEAST likely to be directly proportional?.
Answers
Answer:
Hours worked and money earned
Distance and time when speed is constant
Area and side length of a square
Total cost and the number of hats purchased
Step-by-step explanation:
. A research study about test anxiety will measure the change in heartrate of the test-taker. The researcher randomly assigns participants into one of two groups, either the Test group or the No-test group (where the first group takes a timed test and the second group reads for the same amount of time). What is the operational definition of the independent variable
Answers
Answer:
Timed test.
Step-by-step explanation:
An operational definition gives exactly what the independent variable means and its mode of measurement. The Independent variable is the variable in a research or experimental study which causes a change in the the measured variable. Hence, the independent variable is the predictor variable. In the study above, the independent variable is the timed test which is used to observe changes in the heart rate of the test taker (test anxiety). The change innheartrate of the test taker is the dependent variable.
is 4.333 a irrational number
Answers
No it is not an irrational number
If the radioactive half-life of a substance is 20 days, and there are 5 grams of it initially. When will the amount left be 2 grams? Round to the nearest tenth of a day.
Answers
Answer: \(26.4\ \text{days}\)
Step-by-step explanation:
Given
Half life of radioactive substance is \(T_{\frac{1}{2}}=20\ \text{days}\)
Initial amount \(A_o=2\ \text{days}\)
Amount left at any time is given by
\(\Rightarrow A=A_o2^{\dfrac{-t}{T_{\frac{1}{2}}}}\\\\\Rightarrow 2=52^{\dfrac{-t}{20}}\\\\\Rightarrow 0.4=2^{\dfrac{-t}{20}}\\\\\Rightarrow 2^{\dfrac{t}{20}}=2.5\\\\\Rightarrow \dfrac{t}{20}\ln 2=\ln (2.5)\\\\\Rightarrow t=\dfrac{20\ln (2.5)}{\ln 2}\\\\\Rightarrow t=26.4\ \text{days}\)
It takes 26.4 days to reach 2 gm.
3 1/2 + 7/5 simplified
Answers
Answer:
4 9/10
Step-by-step explanation:
3 1/2 ---- 3 5/10
7/5 ------ 14/10
3 5/10 + 14/10 = 3 19/10 ---- 4 9/10
y=2x+6,2x-y=2 system of equation
Answers
(-1, 6) (x -9) determine value of x algebraically, show work.
Please help i legit cannot understand this, will offer brainliest
Answers
1. Multiply the sides
2. Get what x equals which is 6
What interval will contain 68 percent of the data if the mean is
11 and standard deviation is 2.75 ?
Level of difficulty = 2 of 2
Please format to 2 decimal places.
Answers
The interval that will contain 68 percent of the data, given a mean of 11 and a standard deviation of 2.75, is (8.25, 13.75).
To find the interval, we need to consider the empirical rule (also known as the 68-95-99.7 rule) for a normal distribution. According to this rule, approximately 68 percent of the data falls within one standard deviation of the mean.
Since the mean is 11 and the standard deviation is 2.75, we can calculate the lower and upper bounds of the interval by subtracting and adding one standard deviation, respectively.
Lower bound = 11 - (1 * 2.75) = 8.25
Upper bound = 11 + (1 * 2.75) = 13.75
Therefore, the interval that will contain 68 percent of the data is (8.25, 13.75), which means that approximately 68 percent of the data points will fall within this range.
LEARN MORE ABOUT standard deviation here: brainly.com/question/29115611
#SPJ11