15x⁴-16x³+0x²+8x-17 ÷ (3x²+x+1)
Answers
After dividing ( 15 x⁴ - 16 x³ + 10 x² + 8 x - 17 ) ÷ ( 3 x² + x + 1 ), we get the quotient as 5 x² - 7 x + 4 and the remainder as 11 x - 21.
We are given an expression:
( 15 x⁴ - 16 x³ + 10 x² + 8 x - 17 ) ÷ ( 3 x² + x + 1 )
We need to perform division of the algebraic expression:
5 x² - 7 x + 4
3 x² + x + 1 √15 x⁴ - 16 x³ + 10 x² + 8 x - 17
15 x⁴ + 5 x³ + 5 x²
______________________
- 21 x³ + 5 x² + 8 x - 17
- 21 x³ - 7 x² - 7 x
______________________
12 x² + 15 x - 17
12 x² + 4 x + 4
______________________
11 x - 21
______________________
Therefore, after dividing ( 15 x⁴ - 16 x³ + 10 x² + 8 x - 17 ) ÷ ( 3 x² + x + 1 ), we get the quotient as 5 x² - 7 x + 4 and the remainder as 11 x - 21.
Learn more about division here:
https://brainly.com/question/25289437
#SPJ9
Related Questions
Sausages come in packets of 12. Bread rolls come in packets of 9. Brian wants to buy enough packs of sausages and rolls so that there are an equal number of sausages and rolls. What is the minimum number of sausages and rolls he needs to buy?
Answers
Explanation:
I do guess and check.
12(1) + 9(1) = 12 + 9
12(2) + 9(2) = 24 + 18
12(3) + 9(3) = 36 + 27
12(3) + 9(4) = 36 + 36
So that’s the answer
please help I will give you any award

Answers
Answer:
218.57
Step-by-step explanation:
Since it is an isoceles triangle, the sides are 32, 32, and 14.
Using Heron's Formula, which is Area = sqrt(s(s-a)(s-b)(s-c)) when s = a+b+c/2, we can calculate the area.
(A+B+C)/2 = (32+32+14)/2=39.
A = sqrt(39(39-32)(39-32)(39-14) = sqrt(39(7)(7)(25)) =sqrt(47775)= 218.57.
Hope this helps have a great day :)
Check the picture below.
so let's find the height "h" of the triangle with base of 14.
\(\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies o=\sqrt{c^2 - a^2} \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{32}\\ a=\stackrel{adjacent}{7}\\ o=\stackrel{opposite}{h} \end{cases} \\\\\\ h=\sqrt{ 32^2 - 7^2}\implies h=\sqrt{ 1024 - 49 } \implies h=\sqrt{ 975 }\implies h=5\sqrt{39} \\\\[-0.35em] ~\dotfill\)
\(\stackrel{\textit{area of the triangle}}{\cfrac{1}{2}(\underset{b}{14})(\underset{h}{5\sqrt{39}})}\implies 35\sqrt{39} ~~ \approx ~~ \text{\LARGE 218.57}\)

\( \sqrt[14]{6.3} \)need help showing my son how to solve this problem. explanation is key.
![[tex] \sqrt[14]{6.3} [/tex]need help showing my son how to solve this problem. explanation is key.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/nuHY62ZKttDWALoNx1Cnl0nMyoSt8hpt.jpeg)
Answers
Divide 6.3 meters of leather
between 14
Then
6.3 meters= 630 cm
Now divide
630/14 =
Find m,c,d (max common divisor), between 63 and 14. Its 7.
divide by 7, both numerator and denominator
90/2 = 45
Then answer is , each piece is 45 cm long
write the equation in spherical coordinates. (a) x2 + y2 + z2 = 25
Answers
The equation in spherical coordinates is ρ = 5. This equation represents a sphere centered at the origin with a radius of 5 units in the ρ direction.
To write the equation \(x^2 + y^2 + z^2 = 25\) in spherical coordinates, we need to express x, y, and z in terms of the spherical coordinates (ρ, θ, φ).
In spherical coordinates, ρ represents the distance from the origin to the point, θ represents the azimuthal angle measured from the positive x-axis in the xy-plane, and φ represents the polar angle measured from the positive z-axis.
To transform the Cartesian coordinates (x, y, z) to spherical coordinates, we can use the following equations:
x = ρ sin(φ) cos(θ)
y = ρ sin(φ) sin(θ)
z = ρ cos(φ)
Now let's substitute these equations into the given equation:
\((x^2) + (y^2) + (z^2) = 25\)
(ρ sin(φ) cos(θ))² + (ρ sin(φ) sin(θ))² + (ρ cos(φ))² = 25
ρ² (sin²(φ) cos²(θ) + sin²(φ) sin²(θ) + cos²(φ)) = 25
ρ² (sin²(φ) (cos²(θ) + sin²(θ)) + cos²(φ)) = 25
ρ²(sin²(φ) + cos²(φ)) = 25
ρ²= 25
This simplifies to:
ρ = 5
Therefore, the equation in spherical coordinates is ρ = 5. This equation represents a sphere centered at the origin with a radius of 5 units in the ρ direction.
In spherical coordinates, the equation ρ = 5 describes all points that are at a distance of 5 units from the origin, regardless of the values of θ and φ.
For more such questions on spherical coordinates visit:
https://brainly.com/question/29555384
#SPJ11
When Jake volunteers at the animal shelter, he divides 2/3 cup of cat food equally between 2 cats. How much food does he give each cat?Use the area model

Answers
1/3
each cat gets 1/3 of the food because 2/3 ÷ 2/1 = 1/3.
I NEED HELP ASAP WORTH 50

Answers
Answer:
10 inches
Step-by-step explanation:
┏┓ OK!
┃┣━┓
┛┣━┃
⠀┣━┃
┓┣━┃
┗┻━┛
Find the values of x and y.

Answers
Answer:
x = 12 , y = 60
Step-by-step explanation:
The figure has 2 pairs of parallel sides and is therefore a parallelogram.
The opposite sides and opposite angles are congruent , then
x + 3 = 15 ( subtract 3 from both sides )
x = 12
and y = 60
A cube has a surface area of 150
cm squared. Find the side length of the cube in cm.
Answers
Answer:
Step-by-step explanation:
6 faces have an area of 150 cm^2
1 face has an area of 150/6 = 25 cm^2
The formula for the area of one face of a cube = s^2 which is the length of a side squared.
s^2 = 25
sqrt(s^2) = sqrt(25)
s = 5
What are the forms of protectionism in trade?
Answers
Answer:
Tariffs
Quotas
Export subsidies
Domestic subsidies
Import licensing
Exchange controls
Financial protectionism
Murky or hidden protectionism
Can someone help me please?
A.0.36
B.0.55
C.0.18
D.0.45

Answers
Answer:
B
Step-by-step explanation:
44/77
=0.55
Find the surface area of the figure. Do NOT include units.

Answers
The surface area of the rectangular prism figure is S = 838 cm²
Given data ,
The formula for the surface area of a prism is SA=2B+ph, where B, is the area of the base, p represents the perimeter of the base, and h stands for the height of the prism
Surface Area of the prism = 2B + ph
So, the value of S is given by
The heights of the prism is represented as 7cm.
S = ( 11 x 20 ) + ( 7 x 20 ) + ( 4 x 20 ) + 2( 5 x 7 ) + 2( 6 x 4 ) + ( 6 x 20 ) + ( 5 x 20 ) + ( 3 x 20 )
On simplifying the equation , we get
S = 220 + 140 + 80 + 70 + 48 + 120 + 100 + 60
S = 838 cm²
Therefore , the value of S is 838 cm²
Hence , the surface area is S = 838 cm²
To learn more about surface area of prism click :
https://brainly.com/question/9183590
#SPJ1
Write the slope intercept form of the equation of the line

Answers
Answer:
y= x + 2
Step-by-step explanation:
I need help please i don't get this.

Answers
Answer:
22
Step-by-step explanation:
Points Y and X are are the midpoints of the segments HI and HG respectively.
Therefore,
By Mid-segment formula:
IG = 2*YX = 2* 11 = 22 units
A scientist was in a submarine, 27.4 feet below sea level, studying ocean life. Over the next ten minutes, she went down 23.8 feet. How many feet was she now below sea level?
Answers
Answer:
She was initially at a depth of 24.7 feet before she rose
Step-by-step explanation:
Figure PQRS is dilated by a scale factor of 2 with the center of dilation at the origin. What are the coordinates of point S'?
Answers
Answer:
To dilate by a scale factor of 2, multiply the length of each side of the shape by 2. If the shape is on a coordinate plane, multiply the coordinates of each vertex of the shape by 2.
Hope it helps
A work sampling study is to be performed on an office pool consisting of 10 persons to see how much time they spend on the telephone. The duration of the study is to be 22 days, 7hr/day. All calls are local. Using the phone is only one of the activities that members of the pool accomplish. The supervisor estimates that 25% of the workers time is spent on the phone. (a) At the 95% confidence level, how many observations are required if the lower and upper limits on the confidence interval are 0.20 and 0.30. (b) Regardless of your answer to (a), assume that 200 observations were taken on each of the 10 workers (2000 observations total), and members of the office pool were using the telephone in 590 of these observations. Construct a 95% confidence interval for the true proportion of time on the telephone. (c) Phone records indicate that 3894 phone calls (incoming and outgoing) were made during the observation period. Estimate the average time per phone call.
Answers
coreect answer is (a) A minimum of 385 observations are required at the 95% confidence level to estimate the time spent on the phone in the office pool.
What is the required sample size at a 95% confidence level to estimate phone usage in an office pool through work sampling?
we consider the desired confidence level, to determine the required number of observations, estimated proportion, and margin of error. With the supervisor's estimate that 25% of the workers' time is spent on the phone, we use a formula to calculate the sample size. Using a 95% confidence level and the given lower and upper limits, the margin of error is determined as 0.05. Plugging these values into the formula, we find that a minimum of 385 observations are needed to estimate the time spent on the phone with 95% confidence.
Learn more about confidence intervals
#SPJ11
compute the general term a n an of the series with the partial sum s n = 5 − 5 n , n > 1
Answers
The general term of the series is a_n = -5.
What is the general term of the series?
The compute the general term a_n of the series, we first need to find the formula for the individual terms. We know that the partial sum s_n is given by the formula s_n = 5 - 5n. This means that the sum of the first n terms of the series is equal to 5 - 5n.
To find the formula for the general term a_n, we need to look at the difference between consecutive terms in the series. We know that the nth term of the series is equal to the sum of the first n terms minus the sum of the first n-1 terms.
So, we have:
a_n = s_n - s_{n-1}
Substituting the formula for s_n, we get:
a_n = (5 - 5n) - (5 - 5(n-1))
Simplifying, we get:
a_n = -5
Therefore, the general term of the series is a_n = -5.
Learn more about series.
brainly.com/question/15415793
#SPJ11
in 6th grade math big ideas math 4.3 extension kinda is confusing i got a little but the bottom triangle is confusing

Answers
Answer: 36
Step-by-step explanation:
6 x 4 = 24 (top box)
(6 x 4) divided by 2 = 12 (bottom triangle)
If P(B)=0.3,P(A∣B)=0.5,P(B ′ )=0.7, and P(A∣B ′ )=0.8, find P(B∣A).
Answers
If P(B)=0.3, P(A|B)=0.5, P(B')=0.7and P(A|B')=0.8, then the value of the probability P(B|A)= 0.2113
To find the value of P(B|A), follow these steps:
The probability of B given A can be given by the product of the probability of A given B and the probability of B, divided by the total probability of B. So, the formula for P(B|A) = P(A|B) * P(B) / [P(A|B)*P(B)+P(A|B')*P(B')]. Substituting the values, we get P(B|A) = (0.5) (0.3) / [(0.5) (0.3) + (0.8) (0.7)] ⇒P(B|A) = 0.15 / [0.15 + 0.56] ⇒P(B|A) = 0.15 / 0.71 ⇒P(B|A) = 0.2113. Therefore, P(B|A) = 0.2113.Learn more about probability:
brainly.com/question/13604758
#SPJ11
Determine whether y varies directly with x . If so, find the constant of variation.
y=-2 x
Answers
The required value of the constant of proportion is 2.
What is the constant of proportion?
A constant of proportion is illustrated as the ratio which relates two given quantities with each other in the relationship of proportion. Constant of proportion is also called constant variation, rate of change, and constant ratio.
Solving for the value of constant of variation
When a quantity varies directly with others, then we have a relation, y = kx, where k is the constant of the proportion —-- 1
Given the relation is y = 2x —-- 2
On comparing both the equation 1 and 2, we have,
k = 2
Hence, the required value of constant of variation is 2.
To learn more about the constant of proportion, visit the link:
https://brainly.com/question/24868934
#SPJ4
All of the y values or outputs are called what?
Answers
Answer:
range
Step-by-step explanation:
the x values or inputs are called the domain
the y values or outputs are called the range
Solve 272 - 10 = r2 using square roots. Select the solution(s).
Answers
Calculate the square root in both sides of the calculation:
Distribute the square roots
Simplify the square roots.
\(\begin{gathered} 272=16\cdot17 \\ \sqrt[]{272}=\sqrt[]{16}\cdot\sqrt[]{17} \\ \sqrt[]{272}=4\cdot\sqrt[]{17} \end{gathered}\)Then:
\(\begin{gathered} \sqrt[]{r^2}=\sqrt[]{272-10} \\ r=\sqrt[]{272}-\sqrt[]{10} \\ r=4\sqrt[]{17}-\sqrt[]{10} \end{gathered}\)if T=1/4 A^3B make A the subject of formula
Answers
Step-by-step explanation:
A³B = 4T
A³=4T/B
A = cbrt 4T/B. or
³√(4T/B)
hope this helps.
(a) Suppose that a COVID-19 vaccine is 86% effective in preventing the disease when a person is exposed to the virus. If four vaccinated people are exposed to the virus, find the probability that at least one of them contract the disease. ANSWER = 0.4530
(b) Suppose that 89% of adults in Ontario have been fully vaccinated against COVID-19 and that 71% of adults in Quebec have been fully vaccinated. A random sample consists of one adult from Ontario and one adult from Quebec. Let X be the number of people in the sample that have been fully vaccinated. Find the mean of X. ANSWER = 1.60
(c) Suppose that 63% of all COVID-19 cases in people aged 75-80 require hospitalization. During a recent outbreak at a long term care facility, 13 people aged 75-80 contracted COVID-19 and 10 of those people require hospitalization. Is this number significantly high?
Answers
a. 0.9996 which is approximated to 0.4530 is the probability that at least one of them, b. The mean of X is 1.60, c. the proportion of COVID-19 cases requiring hospitalization is significantly higher than 0.63.
(a) Suppose that a COVID-19 vaccine is 86% effective in preventing the disease when a person is exposed to the virus. If four vaccinated people are exposed to the virus, the probability that at least one of them contracts the disease is 0.4530.
The probability that a vaccinated person does not contract the disease is:1 - 0.86 = 0.14
The probability that all four vaccinated people do not contract the disease is:0.14 x 0.14 x 0.14 x 0.14 = 0.00038
So the probability that at least one of the four vaccinated people contracts the disease is:
1 - 0.00038 = 0.99962P(at least one vaccinated person contracts the disease) = 0.99962P(at least one vaccinated person does not contract the disease)
= 1 - 0.99962 = 0.00038P(at least one of the four vaccinated people contracts the disease) = 1 - P(none of the four vaccinated people contracts the disease)
= 1 - 0.00038 = 0.9996 which is approximated to 0.4530
(b) Suppose that 89% of adults in Ontario have been fully vaccinated against COVID-19 and that 71% of adults in Quebec have been fully vaccinated. A random sample consists of one adult from Ontario and one adult from Quebec. Let X be the number of people in the sample that have been fully vaccinated.
The mean of X is given by :E(X) = np where n is the sample size and p is the probability of success in the population The sample size is 2The probability of success for Ontario is 0.89
The probability of success for Quebec is 0.71
The expected value of X is: E(X) = 2(0.89) + 0(1 - 0.89)(1 - 0.71) = 1.60
The mean of X is 1.60
(c) Suppose that 63% of all COVID-19 cases in people aged 75-80 require hospitalization. During a recent outbreak at a long-term care facility, 13 people aged 75-80 contracted COVID-19 and 10 of those people require hospitalization. To find out whether the number of people requiring hospitalization is significantly high, we need to perform a hypothesis test using the binomial distribution.
Hypotheses:H0: p ≤ 0.63 (The proportion of COVID-19 cases requiring hospitalization is less than or equal to 0.63.)H1: p > 0.63 (The proportion of COVID-19 cases requiring hospitalization is greater than 0.63.)
We will use a significance level of α = 0.05.T
he sample size n is 13.The number of successes (people requiring hospitalization) is 10.The null hypothesis assumes that the proportion of successes is less than or equal to 0.63.
Under this assumption, the mean and standard deviation of the binomial distribution are given by:
μ = np = 13(0.63) = 8.19σ = sqrt(np(1 - p)) = sqrt(13(0.63)(1 - 0.63))
= 1.99
To calculate the z-score, we use the formula: z = (x - μ) / σwhere x is the observed number of successes, μ is the mean, and σ is the standard deviation.
z = (10 - 8.19) / 1.99
= 0.91
The p-value can be found using a standard normal table or calculator. The p-value is the probability of observing a z-score of 0.91 or higher when the null hypothesis is true.
For a one-tailed test at α = 0.05, the critical z-value is 1.645. Since the observed z-score is less than the critical value, we fail to reject the null hypothesis.
There is not enough evidence to conclude that the proportion of COVID-19 cases requiring hospitalization is significantly higher than 0.63.
To know more about probability visit:
brainly.com/question/31828911
#SPJ11
Choose the graph that matches the given equation y = 2sin(x – π) + 2.
On a coordinate plane, a function has a maximum of 4 and minimum of 0. It completes one period at 2 pi. The curve crosses the y-axis at (0, 0).
On a coordinate plane, a function has maximum of 3 and minimum of 1. It completes one period at 2 pi. It decreases through the y-axis and (0, 2).
On a coordinate plane, a function has a maximum of 3 and minimum of 1. It completes one period at 2 pi. It crosses the y-axis at (0, 1).
On a coordinate plane, a function has a maximum of 4 and minimum of 0. It completes one period at 2 pi. It decreases through the y-axis at (0, 2).

Answers
The graph that matches sine function y = 2 sin (x – π) + 2 is:
On a coordinate plane, a function has a maximum of 4 and minimum of 0. It completes one period at 2 pi. It decreases through the y-axis at (0, 2).
What is graph?A graph is a pictorial representation of data. Graphs are usually plotted in a cartesian plane having x and y directions
The graph in the given problem is a graph showing sin function representing sinusoidal waves.
The given equation: y = 2 sin (x – π) + 2
substituting x = 0
y = 2 sin (0 – π) + 2
y = 2 sin (-π ) + 2 (in radians)
y = 2 * 0 + 2
y = 0 + 2
y = 2
Therefore the ordered pair is correct for the graph (0, 2)
Learn more about sine graphs here:
https://brainly.com/question/2491845
#SPJ1
Answer: The answer is D (the last option)
Step-by-step explanation:
Do what the picture says and right answer gets brainilest!!!

Answers
Answer:
Below
Step-by-step explanation:
See image attached
A gas station sells unleades regular petrol and preminum charged by station for regular is$1.299
Answers
Answer:
a. Assuming gallons of unleaded regular is denoted by r; and unleaded premium by p.
Revenue from one gallon of unleaded regular is $1.299 and from unleaded premium is $1.379.
Revenue function = 1.299r + 1.379p
b. Cost of one gallon of unleaded regular is $1.219 and for unleaded premium is $1.289.
Cost function = 1.219r + 1.289p
c. Total profit = Revenue - Cost
= 1.299r + 1.379p - 1.219r - 1.289p
= 1.299r - 1.219r + 1.379p - 1.289p
= 0.08p + 0.09p
d. If station sells 100,000 gallons of unleaded regular and 40,000 of unleaded premium;
= (0.08 * 100,000) + (0.09 * 40,000)
= 8,000 + 3,600
= $11,600
(I BEG YOU HELP ME TUTORS! ITS A MULTIPLE CHOICE ILL GIVE U BRAINLY)

Answers
Answer:
ans= (2)
Step-by-step explanation:
y=x²-1 is the only quadratic function there
1 is a linear function
3 is a cubic function
4 is a a constant function
Please help as soon as possible! Thank you so much!!

Answers
Answer:
3. SAS
4. DEB is congruent to CEA
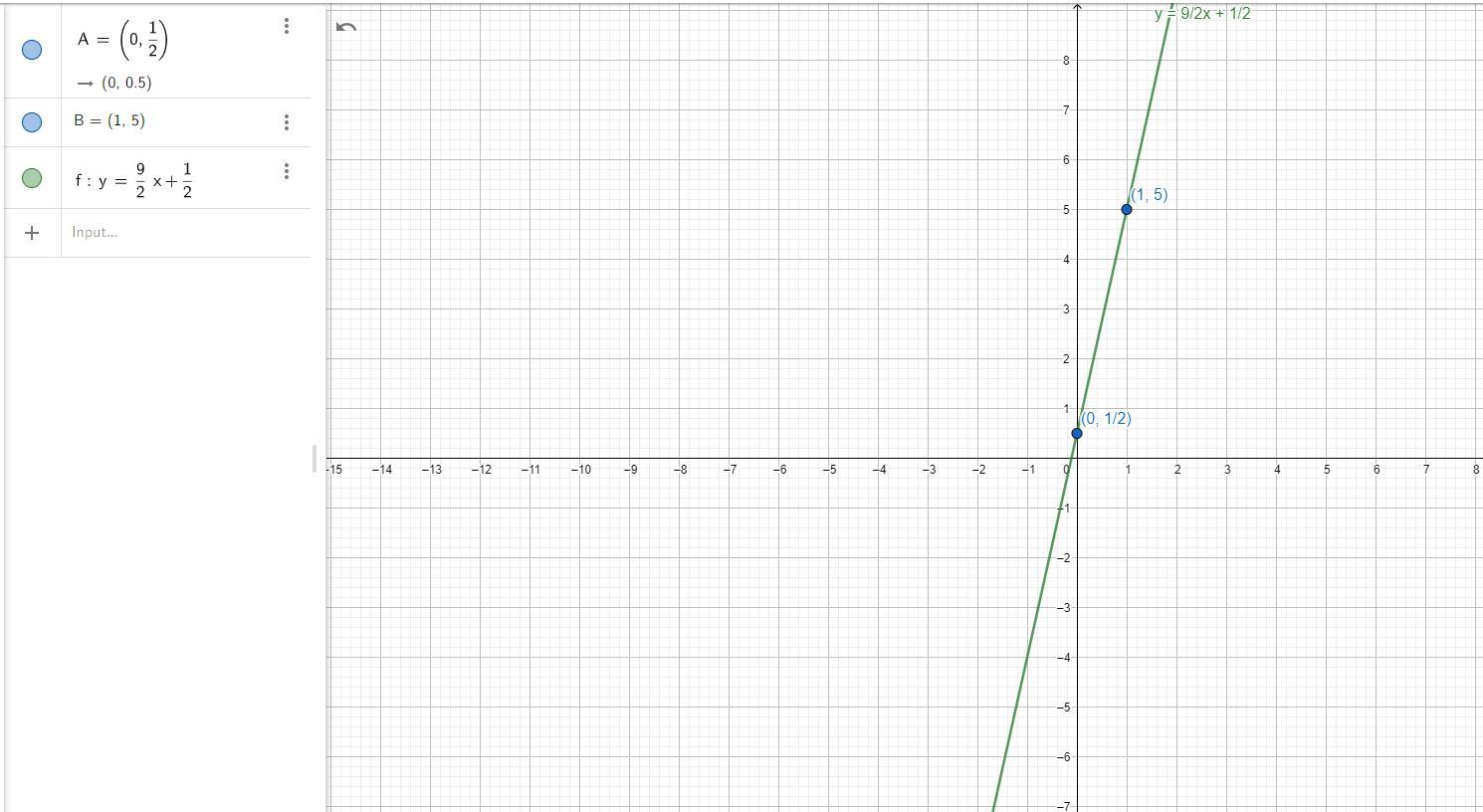
graph the linear equation using the slope intercept form . -11x+2y=1

Answers
We will have the following:
*First: We solve for y:
\(-9x+2y=1\Rightarrow2y=9x+1\)\(\Rightarrow y=\frac{9}{2}x+\frac{1}{2}\)*Second: We determine two sets of points that belong to the line. In our case we will solve for x = 0 & x = 2. So we would get:
*For x = 0:
\(y=\frac{9}{2}(0)+\frac{1}{2}\Rightarrow y=\frac{1}{2}\)So, we would have the point:
\((0,\frac{1}{2})\)*For x = 1:
\(y=\frac{9}{2}(1)+\frac{1}{2}\Rightarrow y=5\)So, we would have the point:
\((1,5)\)*Third: We graph: