15 POINTS :)
Solve the inequality.
-3x+4<25
Answers
Answer:
x > -7
Step-by-step explanation:
-3x + 4 < 25
-3x + 4 - 4 < 25 - 4
-3x < 21
-3x/-3 < 21/-3
x > -7
May i have brainliest? :)
Related Questions
PLEASEEEE HELP!!!The function y=15(0.84)^x models the amount y of a 15mg dose of
antibiotic remaining in the bloodstream after x hours. How much remains
after 8 hours? *
A)7.52mg
B)3.25mg
C)5.63mg
D)03.72mg

Answers
Answer:
3.72
Step-by-step explanation:
y=15(0.84)^8
15*0.84
12.6*8
y=3.72
Answer:
3.72
Step-by-step explanation:
:)
Colin borrowed 4200 at 8% simple interest to be paid back in 3 years. How much interest will he pay
Answers
Answer:
Answer 1008
Step-by-step explanation:
Find the quotient of z₁ by z2. Express your answer in
trigonometric
form.
² - 3 (0 (4) + (*))
Z₁ cos
+/sin
Z₂
²2 = 7 (cos(377)+
COS
8
O A. 7 (cos (577) + i sin (5/77))
8
B.
21(cos(577)+isin (577))
8
OC. 21 cos
21(cos(-7)+ i sin(-77))
O D. 7 (cos(-7) + + sin(-7))
i
+/sin
37T
8

Answers
The quotient of z₁ by z₂ in trigonometric form is:
7/21 * (cos(584°) + i sin(584°))
To find the quotient of z₁ by z₂ in trigonometric form, we'll express both complex numbers in trigonometric form and then divide them.
Let's represent z₁ in trigonometric form as z₁ = r₁(cosθ₁ + isinθ₁), where r₁ is the magnitude of z₁ and θ₁ is the argument of z₁.
We have:
z₁ = 7(cos(577°) + i sin(577°))
Now, let's represent z₂ in trigonometric form as z₂ = r₂(cosθ₂ + isinθ₂), where r₂ is the magnitude of z₂ and θ₂ is the argument of z₂.
From the given information, we have:
z₂ = 21(cos(-7°) + i sin(-77°))
To find the quotient, we divide z₁ by z₂:
z₁ / z₂ = (r₁/r₂) * [cos(θ₁ - θ₂) + i sin(θ₁ - θ₂)]
Substituting the given values, we have:
z₁ / z₂ = (7/21) * [cos(577° - (-7°)) + i sin(577° - (-7°))]
= (7/21) * [cos(584°) + i sin(584°)]
The quotient of z₁ by z₂ in trigonometric form is:
7/21 * (cos(584°) + i sin(584°))
Option C, 21(cos(-7°) + i sin(-77°)), is not the correct answer as it does not represent the quotient of z₁ by z₂.
For more questions on trigonometric form
https://brainly.com/question/31744474
#SPJ8
Uncle Louise is at least 1 inch shorter than Miriam, and at least 2 inches taller than Jeffery. Jeffery's height is 64 inches. Miriam is not more than 5 inches taller than Jeffery. Which answer could be Uncle Louise's height? Please answer!!!
Answers
Answer:
67 inches
Step-by-step explanation:
Let's call the height of Louise 'L', the height of Miriam 'M' and the height of Jeffery 'J'.
Then, we can write the following equations and inequations:
\(L \leq M - 1\)
\(L \geq J + 2\)
\(J = 64\)
\(M \leq J + 5\)
Substituting J in the second and four inequations, we have:
\(L \geq 66\)
\(M \leq 69\)
If we assume the maximum value for M, in the first inequation we have that:
\(L \leq 68\)
So the height of Uncle Louise is greater than or equal 66, and lesser than or equal 68, so his height could be 67 inches for example.
Y=5x+3 graph the line
Answers
Answer:
The graph is in the pic
Step-by-step explanation:

Raj’s bathtub is clogged and is draining at a rate of 1.5 gallons of water per minute. The table shows that the amount of water remaining in the bathtub, y, is a function of the time in minutes, x, that it has been draining. what is the value of this function
Answers
The range of y will be all real numbers such that 0≤y≤40
The complete question is:
Raj’s bathtub is clogged and is draining at a rate of 1.5 gallons of water per minute. The table shows that the amount of water remaining in the bathtub, y, is a function of the time in minutes, x, that it has been draining. What is the range of this function? all real numbers such that y ≤ 40 all real numbers such that y ≥ 0 all real numbers such that 0 ≤ y ≤ 40 all real numbers such that 37.75 ≤ y ≤ 40
What is inequality?The relation between two expressions that are not equal, employing a sign such as ≠ ‘not equal to’, > ‘greater than, or < ‘less than.
Raj’s bathtub is clogged and is draining at a rate of 1.5 gallons of water per minute.
The amount of water remaining in the bathtub = y
The function of time in minutes, that it has been draining = x
At 0 minutes the amount of water is 40 gallons.
The highest volume of water is 40 which is decreasing at the rate of 1.5 gallons per minute.
The given function is a linear function
y = 0
However, the volume of water can be 0 but cannot ever be negative.
Therefore the range of y will be all real numbers such that 0≤y≤40
To know more about inequality follow
https://brainly.com/question/24372553
#SPJ1
-6 + (-3) - (-2) =
A. 11
B. 7
C. -7
D. -11
Answers
Answer:
C. -7
Step-by-step explanation:
C. -7
Step by step explanation:
-6+(-3)-(-2) When there is a in front of an expression in parentheses, the expression remains the same and when there is a in front of an expression in parentheses, change the sign of each term in the expression
-6-3+2= -7
Check all the statements) that are true about the polynomial function graphed
Its leading coefficient is positive. its leading coefficient is negative.
It has an odd degree
It has an even degree
It has exactlv two real zeroes
It has exactly three real zeroes.
None of the zeroes have even multiplicity
None of the zeroes have odd multiplicity.
Answers
The true statements about the polynomial function graphed are:
Its leading coefficient is positive.
It has an odd degree.
None of the zeroes have even multiplicity.
From the given options, the true statements about the polynomial function graphed are:
Its leading coefficient is positive.
It has an odd degree.
None of the zeroes have even multiplicity.
Let's analyze each statement:
Its leading coefficient is positive:
The leading coefficient of a polynomial is the coefficient of the term with the highest degree.
From the graph, if the polynomial is going upwards on the right side, it indicates that the leading coefficient is positive.
It has an odd degree: The degree of a polynomial is the highest power of the variable in the polynomial expression.
If the graph has an odd number of "turns" or "bumps," it indicates that the polynomial has an odd degree.
None of the zeroes have even multiplicity:
The multiplicity of a zero refers to the number of times it appears as a factor in the polynomial.
In the given graph, if there are no repeated x-intercepts or no points where the graph touches and stays on the x-axis, it implies that none of the zeroes have even multiplicity.
The other statements (its leading coefficient is negative, it has an even degree, it has exactly two real zeroes, it has exactly three real zeroes, and none of the zeroes have odd multiplicity) cannot be determined based solely on the information given.
Therefore, the true statements about the polynomial function graphed are:
Its leading coefficient is positive.
It has an odd degree.
None of the zeroes have even multiplicity.
For similar question on polynomial function.
https://brainly.com/question/31528136
#SPJ8
Hello everyone, I'm just having trouble on a question for my Calculus work. Does anyone know where to start with this problem? Any help would be greatly appreciated!

Answers
Answer:
sin(8w)/1024 -sin(4w)/128 +3w/128
Step-by-step explanation:
No doubt there are a variety of formulas and identities that can be used. Absent knowledge of those, I found it convenient to rewrite the integrand using Euler's formula. It tells you ...
\(\sin(x)=\dfrac{e^{ix}-e^{-ix}}{2i},\quad\cos(x)=\dfrac{e^{ix}+e^{-ix}}{2}\)
After some only slightly messy algebra, we find ...
\(\cos^4(w)\sin^4(w)=\dfrac{\cos(8w)-4\cos(4w)+3}{128}\)
Then the integral becomes straightforward:
\(\displaystyle \int{\cos^4(w)\sin^4(w)}\,dw=\int{\dfrac{\cos(8w)}{128}}\,dw-\int{\dfrac{\cos(4w)}{32}}\,dw+\dfrac{3}{128}\int{}\,dw\\\\=\boxed{\dfrac{\sin(8w)}{1024}-\dfrac{\sin(4w)}{128}+\dfrac{3w}{128}}\)
__
Additional comment
The slightly messy algebra involves the identities ...
(a+b)(a-b) = a² -b²
(a -b)⁴ = a⁴ -4a³b +6a²b² -4ab³ +b⁴
Recall the double angle identity for sine:
sin(2x) = 2 sin(x) cos(x)
This means the given integrand is equivalent to
cos⁴(w) sin⁴(w) = (cos(w) sin(w))⁴ = (1/2 sin(2w))⁴ = 1/16 sin⁴(2w)
Also recall the half-angle identities for sine and cosine:
cos²(x) = 1/2 (1 + cos(2x))
sin²(x) = 1/2 (1 - cos(2x))
Then we can rewrite further as
1/16 sin⁴(2w) = 1/16 (sin²(2w))²
… = 1/16 (1/2 (1 - cos(4w)))²
… = 1/16 (1/4 (1 - 2 cos(4w) + cos²(4w))
… = 1/64 (1 - 2 cos(4w) + 1/2 (1 + cos(8w)))
… = 1/128 (3 - 4 cos(4w) + cos(8w))
You'll end up with the same solution as in the other answer:
\(\displaystyle \int \cos^4(w)\sin^4(w) \, dw = \frac1{128} \int (3 - 4\cos(4w) + \cos(8w)) \, dw \\\\ = \frac{3w-\sin(4w)+\frac18\sin(8w)}{128} + C \\\\ = \boxed{\frac{24w-8\sin(4w)+\sin(8w)}{1024} + C}\)
ON A HIGHWAY GOING TO YOUR PROVINCE YOU, NOTICE THAT THERE IS A BILLBOARD LOCATED EVERY 1 1/2 KILOMETERS. THERE ARE 14 BILLBOARDS IN THAT HIGHWAY. HOW LONG IS HIGHWAY
Answers
Answer:
The highway is 21 km long.
Step-by-step explanation:
\(\frac{1 billboard}{1.5 km} =\frac{14 billboard}{x}\)
x = 21 km
Nicole took a friend to the movies. She hought both of their movie tickets and spent $18 on snacks If she spent 533 total how much was each movie ticket?
Answers
Answer:259
Step-by-step explanation:
you subtract 18 from 533 which gets you 518 then divide it by two
A fancy restaurant put dishes of butter at each table. They divided 4/5 of a kilogram of butter evenly to put 1/5 of a kilogram in each dish. How many butter dishes did they fill?
Answers
Answer: 4
This problem requires basic division. If the restaurant divided 4/5 kg of butter with 1/5 kg on each dish, you would need to compute 4/5 divided by 1/5.
4/5 ÷ 1/5
Using the "KFC" method, or Keep, Change, Flip, you would keep the first number (in this case, 4/5), change the division sign, and flip the fraction to 5/1, or 5. We now have this:
4/5 x 5
To compute this equation, you must multiply the numerators of both of the numbers together. In this case, you would compute (4x5)/5, resulting with 20/5, or 4.
You can check this answer by re-multiplying the numbers together. 1/5 kg of butter per dish, multiplied by the total amount of dishes, 4, you would result in the original 4/5 kg of butter.
Hope this helps!
I need help pleaseee

Answers
Answer:
7
Step-by-step explanation:
refer to solution in picture

Someone answered it incorrectly, so please check image.

Answers
Answer: A 1. Linear because it goes up by 100 evenly
A. 2. Exponential because if you look it goes up rapidly and in no pattern .
B. 1. 1300*n= 2100
B. 2. 1331*n=F?
C. If she chooses option 2 she with get a good amount of money more than option 1.
hope this helps
Answer:
Part A)
Option 1 is linear; Option 2 is exponential.
Part B)
\(f(n)_1=100n+1000\\f(n)_2=1000(1.1)^n\)
Part C)
After 20 years, Option 1 yields $3000.
After 20 years, Option 2 yields approximately $6727.50.
Yes, there is a significant difference. Melinda should invest using Option 2.
Step-by-step explanation:
We know that Belinda invested a total of $1000. We also have a table showing the value of her investment.
Part A)
First, let's examine the table for Option 1. We can see that for each year after the deposit, the investment increases by $100. Since Option 1 increases by a constant rate of $100 per year, Option 1 is linear.
For Option 2, we can see that the amount added each year is not constant. For the first year, the investment earned a total of $1100 - $1000 = $100. However, for the second year, the investment earned $1210 - $1100 = $110. And, similarly, for the third year, the investment earned $1331 - $1210 = $121.
Therefore, the the rate is not constant, Option 2 is exponential.
Part B)
For Option 1)
Since it is a linear function, we can use the standard linear function given by:
\(f(n)=mn+b\)
Where m is the slope and b is the y-intercept.
Since we started with $1000, our b is 1000.
And since the investment increases $100 for each year n, our slope m is 100. Therefore:
\(f(n)=100n+1000\)
For Option 2)
Since it is an exponential function, we can use the standard exponential function given by:
\(f(n)=a(r)^n\)
Where a is the initial value and r is the rate of growth.
We don't actually know the rate of growth, but we can find it. First, since the initial investment is $1000, substitute 1000 for a. This yields:
\(f(n)=1000(r)^n\)
Since we know that the investment reached $1100 after one year, let's substitute 1100 for f(n) and 1 for n. This yields:
\(1100=1000(r)^1\)
Divide both sides by 1000. Simplify:
\(r=1.1\)
Therefore, our rate of growth is 1.1. So, our function is:.
\(f(n)=1000(1.1)^n\)
Part C)
To find the investment value after 20 years, we can use. our functions.
For Option 1)
Substitute 20 for n:
\(f(20)=100(20)+1000\)
Evaluate:
\(f(20)=2000+1000=\$3000\)
For Option 2)
Substitute 20 for n:
\(f(20)=1000(1.1)^{20}\)
Evaluate:
\(f(20)\approx\$6727.50\)
Therefore, if we used Option 2, we will earn an additional $6727 - $3000 = $3727. This is hugely significant, so Belinda should invest using Option 2.
If y = 9x − 7, which of the following sets represents possible inputs and outputs of the function, represented as ordered pairs? A) {(0, −7), (1, 2), (−1, −16)} B) {(−7, 0), (2, 1), (−16, −1)} C) {(1, 9), (2, 7), (3, 16)} D) {(7, 9), (8, 10), (9, 11)}
Answers
Answer:
0,-7 8,567;7,57,6,6,6,6,6,78,3,5
1. Pilar and her sister Marisol live near the beach. Pilar has 80 seashells in her collection when Marisol started collecting seashells. Marisol started with zero seashells in her collection. Pilar adds 10 seashells to her collection each week for x weeks. • Marisol adds 20 seashells to her collection each week for x weeks.
(a) Write an inequality to represent the situation when the number of seashells in Marisol's collection is greater than the number of seashells in Pilar's collection
(b) Solve the inequality in part (a) for the x. Show your work and explain your answer.
Answers
Answer:
(0 + 20x) > (80 + 10x)
Number of weeks > 8 weeks
Step-by-step explanation:
Given the following :
Initial Pilar = 80 ; when marisol started, marisol had 0 then,
Pilar adds 10 each week for x weeks
Marisol adds 20 each week for x weeks
Pilar:
Initial + Increment * number of weeks
80 + (10)x
Marisol :
0 + 20x
When marisol will be greater than pilar's function
Marisol > pilar
A.) (0 + 20x) > (80 + 10x)
20x > 80 + 10x
20x - 10x > 80
10x > 80
x > 8
The number of seashells in marisol collection will be greater Than seashells in pilar's collection after 8, weeks
pls help me solve this

Answers
The results of operations between vectors are, respectively:
Case A: u + w = <- 3, - 1>
Case B: - 6 · v = <6, 6>
Case C: 3 · v - 6 · w = <- 21, - 15>
Case D: 4 · w + 3 · v - 5 · u = <39, 4>
Case E: |w - v| = √(4² + 3²) = 5
How to determine the operations between vectors
In this problem we must determine the operations between vectors, this can be done by following definitions:
Vector addition
v + u = (x, y) + (x', y') = (x + x', y + y')
Scalar multiplication
α · v = α · (x, y) = (α · x, α · y)
Norm of a vector
|u| = √(x² + y²)
Now we proceed to determine the result of each operation:
Case A:
u + w = <- 6, - 3> + <3, 2>
u + w = <- 3, - 1>
Case B:
- 6 · v = - 6 · <- 1, - 1>
- 6 · v = <6, 6>
Case C:
3 · v - 6 · w = 3 · <- 1, - 1> - 6 · <3, 2>
3 · v - 6 · w = <- 3, - 3> + <- 18, - 12>
3 · v - 6 · w = <- 21, - 15>
Case D:
4 · w + 3 · v - 5 · u = 4 · <3, - 2> + 3 · <- 1, - 1> - 5 · <- 6, - 3>
4 · w + 3 · v - 5 · u = <12, - 8> + <- 3, - 3> + <30, 15>
4 · w + 3 · v - 5 · u = <39, 4>
Case E:
|w - v| = |<3, 2> - <- 1, - 1>|
|w - v| = |<4, 3>|
|w - v| = √(4² + 3²) = 5
To learn more on vectors: https://brainly.com/question/31900604
#SPJ1
9. Find the value of
the expression.
16 + 4 + (42 - 3) =
Answers
Answer:
59Step-by-step explanation:
16 + 4 + (42 - 3) = 20 + 39 =59Answer:
59
Step-by-step explanation:
16 + 4 + (42-3) = 59. Do parentheses first. (42-3) = 39. Which changes the equation to 16 + 4 + (39). 39 + 4 = 43. Then the equation changes to 16 + 43. These added together equal 59. Hope this helps!
PEMDAS= Parentheses, exponents, multiplication, division, addition, and then subtraction.
This is the order in which to solve these types of equations, which is why I did the parentheses first.
Evaluate and match each expression on the left to it's value on the right, when x=6 and y=5?
12+x
Answers
\(12 + x = 12 + 6\)
\(\implies 12 + x = 18\)
Question 6 of 10
A line of best fit was drawn for 6 data points. What is the maximum number
of these data points that may not actually be on the line?
OA. 6
B. 3
O C. 4
OD. 5
SUBMIT
Answers
Can someone write an equation that represents the information provided
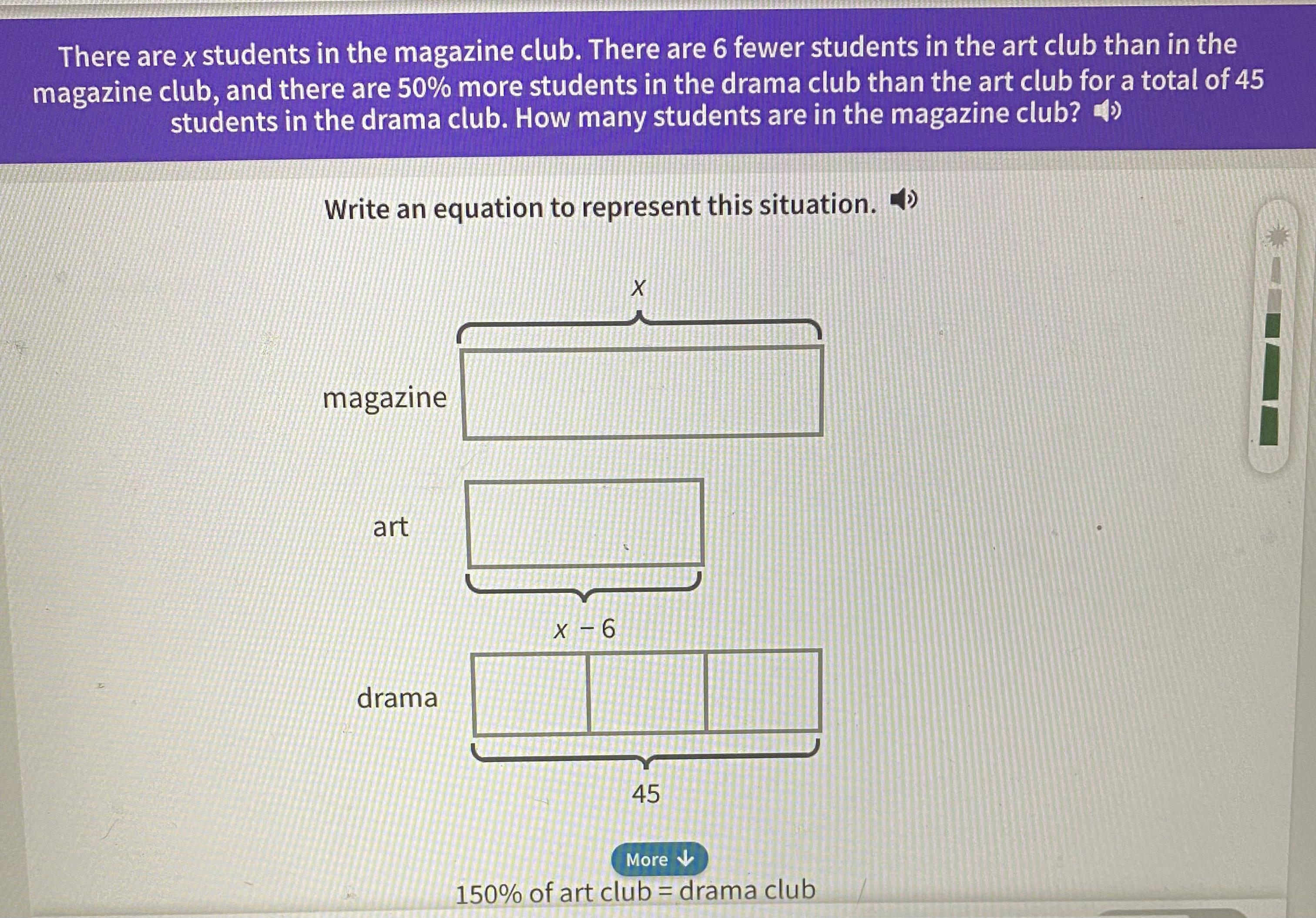
Answers
We first wrote an equation that represents the information provided and found the number of students in the magazine club as 36.
What is an equation?
A mathematical equation is a formula that uses the equals sign (=) to represent the equality of two expressions. The expressions on each side of the equals sign are referred to as the "left-hand side" and "right-hand side," respectively, of the equation. Typically, we consider an equation's right side to be zero. As we can balance this by deducting the right-side expression from both sides' expressions, this won't reduce the generality.
Given,
Total number of students in magazine club = x
Total number of students in art club = x - 6
Total number of students in the drama club = 50% more than art club
So if we consider 100% students in the art club, then
Number of students in the drama club = 50% + 100% = 150% of the art club = 45
1.50( x - 6 ) = 45
This is the equation, representing the given information.
Now solving the above equation, we can find x.
1.5x = 45 + 9
x = 36
Therefore we first wrote an equation that represents the information provided and found the number of students in the magazine club as 36.
To learn more about equations, follow the link.
https://brainly.com/question/22688504
#SPJ1
Three dogs eat 30 pounds of food in 10 days. If each dog eats the same amount, how much food does 1 dog eat in 1 day? 1 pound 3 pounds 9 pounds 10 pounds

Answers
Answer:
Unable to read entire question, but see explanation for answer
Step-by-step explanation:
First, you need to find the unit rate per dog. If it takes 3 dogs 10 days to finish 30 pounds of food, then it takes 1 dog 1 day to finish 1 pound of food. I cannot read the entirety of the question because of the cropping, but you can find how much food a single dog eats in that amount of days by just multiplying by the number of days (say, 1 pound in 1 day, or 3 pounds in 3 days). Hope this helps!
Answer:
1
Step-by-step explanation:
took test
54 - x = 31. What does x Equal
Answers
Answer:
23
Step-by-step explanation:
31+23=54
\(54-x=31\)
Simplify:
\(-x+54=31\)
Subtract 54 from both sides:
\(-x+54-54=31-54\)
\(-x=-23\)
Divide both sides by -1:
\(\dfrac{-x}{-1} =\dfrac{-23}{-1}\)
\(=\fbox{x = 23}\)
Identify the graph of the inequality 2(2x-1)+7< 13 or -2x+5-10.

Answers
From the resulting solution, the correct linear inequality graph is Graph C.
Solving inequality expressionGiven the inequality equation below:
2(2x-1)+7< 13 or -2x+5 ≤ -10.
Simplify the expression
2(2x-1)+7< 13
Expand
4x - 2 + 7 < 13
4x + 5 < 13
4x < 13 - 5
4x < 8
x < 2
For the inequality -2x+5 ≤ -10.
-2x+5 ≤ -10
-2x ≤ -15
x ≥ 7.5
Hence the solution to the given system of inequalities are x < 2 and x ≥ 7.5
Learn more on inequality graph here: https://brainly.com/question/24372553
#SPJ1
Challenger Elementary School has 800 students. Every
Wednesday, 12% of the students stay after school for
Chess Club.
How many students attend Chess Club on Wednesdays?
Answers
Answer:
96 students attend Chess club
Step-by-step explanation:
800x.12=96
Answer:
96 students.
Step-by-step explanation:
x=800/12%
Convert the percentage to a decimal.
12%/100=0.12
Multiply the decimal by the total number.
0.12x800=96
Hope this helps :)
Burning Brownie has five varieties of cakes as Chocolate fudge cake (Cake 1), Nutella-filled Cake (Cake 2), Marble Cake (Cake 3), Cheese cake (Cake 4) and Fruit Cake (Cake 5) at their store. The selling prices of each of the cakes are $9, $12, $4, $5, $8 respectively. a. Formulate the Revenue function If it takes 4 cups of milk, 7 cups of sugar, 1 egg, 3 cups flour & 4 cups cream to make Cake 1; 3 cups milk, 4 cups sugar, 2 egg, 4 cups flour & no cream to make Cake 2; 1 cups milk, 5 cups sugar, 3 eggs, 2 cups flour & 1 cup cream to make Cake 3; 5 cups milk, no sugar, 4 eggs, 4 cups flour & 5 cups cream for Cake 4; & lastly 4 cups milk, 8 cups sugar, 5 eggs, 6 cups flour & 3 cups cream to make Cake 5; Which types of cakes to be baked such that we get maximum Revenue? Keep in mind that the store has availability of maximum 280 cups milk, 300 cups sugar, 80 eggs, 250 cups flour & 190 cups cream at their disposal. b. Formulate the constraints of the scenario. c. Solve the system if linear inequalities using Excel Solver.
Answers
A. In equation form: Revenue = 9x1 + 12x2 + 4x3 + 5x4 + 8x5
B. Non-negativity constraint: x1, x2, x3, x4, x5 ≥ 0
How did we get these values?To solve this problem using E x c e l Solver, set up the revenue function and the constraints. Here's how you can do it:
a. Revenue Function:
Let's denote the number of cakes baked for each type as x1, x2, x3, x4, and x5 respectively.
The revenue function can be formulated as:
Revenue = (Selling Price of Cake 1 × Number of Cake 1) + (Selling Price of Cake 2 × Number of Cake 2) + (Selling Price of Cake 3 × Number of Cake 3) + (Selling Price of Cake 4 × Number of Cake 4) + (Selling Price of Cake 5 × Number of Cake 5)
In equation form:
Revenue = 9x1 + 12x2 + 4x3 + 5x4 + 8x5
b. Constraints:
The constraints for the availability of ingredients can be formulated as follows:
Milk constraint: 4x1 + 3x2 + x3 + 5x4 + 4x5 ≤ 280
Sugar constraint: 7x1 + 4x2 + 5x3 ≤ 300
Egg constraint: x1 + 2x2 + 3x3 + 4x4 + 5x5 ≤ 80
Flour constraint: 3x1 + 4x2 + 2x3 + 4x4 + 6x5 ≤ 250
Cream constraint: 4x1 + 5x3 + x4 + 3x5 ≤ 190
Non-negativity constraint: x1, x2, x3, x4, x5 ≥ 0
c. Solve the system of linear inequalities using E x c e l Solver:
To solve the system of linear inequalities using E x c e l Solver, follow these steps:
1. Open M i c r o s o f t E x c e l and enter the following data in a new sheet:
| | A | B |
|-----|-----------|-----------------|
| 1 | Cakes | Selling Price |
| 2 | Cake 1 | $9 |
| 3 | Cake 2 | $12 |
| 4 | Cake 3 | $4 |
| 5 | Cake 4 | $5 |
| 6 | Cake 5 | $8 |
| | | |
| | | Formula |
| 9 | Milk | 280 |
| 10 | Sugar | 300 |
| 11 | Eggs | 80 |
| 12 | Flour | 250 |
| 13 | Cream | 190 |
2. In cell B16, enter the formula for the revenue:
=B2×B7 + B3×B8 + B4×B9 + B5×B10 + B6×B11
3. In cell B18, enter the formula for the milk constraint:
=4×B2 + 3×B3 + B4 + 5×B5 + 4×B6
4. In cell B19, enter the formula for the sugar constraint:
=7×B2 + 4×B3 + 5×B4
5. In cell B20, enter the formula for the egg constraint:
=B2 + 2×B3 + 3×B4 + 4×B5 + 5×B6
6. In cell B21, enter the formula for the flour constraint:
=3×B2 + 4×B3 + 2×B4 + 4×B5 + 6×B6
7. In cell B22, enter the formula for the cream constraint:
=4×B2 + 5×B4 + B5 + 3×B6
8. In cell B24, enter the formula for the non-negativity constraint for Cake 1:
=B2
9. Repeat step 8 for the remaining cakes, entering the formulas in cells B25, B26, B27, and B28:
=B3
=B4
=B5
=B6
10. Now, select cells B16 to B28 and click on the "Solver" button in the "Data" tab.
11. In the Solver Parameters window, set the objective to maximize the cell B16 (Revenue).
12. Set the By Changing Variable Cells to B24:B28 (the number of cakes baked).
13. Click on the "Add" button in the "Subject to the Constraints" section.
14. In the Constraint window, select the range B18:B22 for the constraint cells.
15. In the Solver Parameters window, click on the "Add" button again and select the range B24:B28 for the non-negativity constraints.
16. Set the Solver options as desired, and click on the "Solve" button.
E x c e l Solver will calculate the optimal values for the number of cakes to be baked for each type that maximize the revenue, while satisfying the given constraints on ingredient availability. The solution will be displayed in cells B24:B28, indicating the number of cakes to be baked for each type.
learn more about excel solver: https://brainly.com/question/31404959
#SPJ1
Wyatt was out at a restaurant for dinner when the bill came. He wanted to leave a tip of 19%. What number should he multiply the cost of the meal by to find the total plus tip in one step?
Answers
Answer:
The cost of the meal should be multiplied by 1.19.---------------------------------------
Let the cost of the meal be x.
Adding a tip of 19%:
x + 19% = x + 0.19x = x (1 + 0.19) = 1.19xAnswer:
Wyatt should multiply with 1.19.
Step-by-step explanation:
Forming the expression,
→ 1 + (19% of 1)
Now the required number is,
→ 1 + (19% of 1)
→ 1 + ((19/100) × 1)
→ 1 + (19/100)
→ 1 + 0.19 = 1.19
Hence, required number is 1.19.
What is the area of the square that measures 3.1 m on each side
Answers
The area of the square with a side length of 3.1 meters is 9.61 square meters.
To find the area of a square, we need to multiply the length of one side by itself. In this case, the square has a side length of 3.1 m.
Area of a square = side length × side length
Substituting the given side length into the formula:
Area = 3.1 m × 3.1 m
To perform the calculation:
Area = 9.61 m²
It's worth noting that when calculating the area, we are working with squared units. In this case, the side length is in meters, so the area is expressed in square meters (m²). The area represents the amount of space enclosed within the square.
Remember, to find the area of any square, you simply need to multiply the length of one side by itself.
The area of the square with a side length of 3.1 meters is 9.61 square meters.
For more such questions on square
https://brainly.com/question/27307830
#SPJ8
a rectangle is 100x500 yards what is the square yards
Answers
Answer:
It is 50000 sq. Yards.
Hope it helps
Un gerente de oficina pide una calculadora o un calendario para cada uno de los 60 empleados de la oficina. Cada calculadora cuesta $15 y cada calendario cuesta $10. El pedido total ascendió a $800. Parte A: Escribe el sistema de ecuaciones que modela este escenario. (5 puntos) Parte B: Utilice el método de sustitución o el método de eliminación para determinar el número de calculadoras y calendarios pedidos. Mostrar todos los pasos necesarios. (5 puntos)
Answers
The system of equations is
15x + 10y = 800
x + y = 60
and the solution to these equations is
x = 40
y = 20
What are algebraic expressions?In mathematics, an expression or mathematical expression is a finite combination of symbols that is well-formed according to rules that depend on the context.Mathematical symbols can designate numbers (constants), variables, operations, functions, brackets, punctuation, and grouping to help determine order of operations and other aspects of logical syntax.Given is that an office manager requests a calculator or calendar for each of the 60 office employees. Each calculator is $15 and each calendar is $10. The total order amounted to $800.
We can write the system of equations as -
15x + 10y = 800
x + y = 60
We can write -
y = 60 - x
So, we can write -
15x + 10(60 - x) = 800
15x - 10x + 600 = 800
5x = 200
x = 40
Then -
y = 20
Therefore, the system of equations is
15x + 10y = 800
x + y = 60
and the solution to these equations is
x = 40
y = 20
To solve more questions on algebraic expressions, visit the link below-
brainly.com/question/1041084
#SPJ1
{Question in english is -
An office manager requests a calculator or calendar for each of the 60 office employees. Each calculator is $15 and each calendar is $10. The total order amounted to $800. Part A: Write the system of equations that models this scenario. (5 points) Part B: Use the substitution method or the elimination method to determine the number of calculators and calendars ordered. Show all the necessary steps. (5 points)
}