1.4y+0.09y=1.49 what is y

The complex numbers -2.7e^(√7) + 4.3e^(√5) can be expressed as approximately -6.488 - 0.166i in rectangular form and approximately 6.494 ∠ -176.14° in polar form.

To express the given complex numbers in rectangular form and polar form, we need to understand the representation of complex numbers using exponential form and convert them into the desired formats. In rectangular form, a complex number is expressed as a combination of a real part and an imaginary part in the form a + bi, where 'a' represents the real part and 'b' represents the imaginary part.

In polar form, a complex number is represented as r∠θ, where 'r' is the magnitude or modulus of the complex number and θ is the angle formed with the positive real axis.

To convert the given complex numbers into rectangular form, we can use Euler's formula, which states that e^(ix) = cos(x) + isin(x), where 'i' is the imaginary unit. By substituting the given values, we can calculate the real and imaginary parts separately.

The real part can be found by multiplying the magnitude with the cosine of the angle, and the imaginary part can be obtained by multiplying the magnitude with the sine of the angle.

After performing the calculations, we find that the rectangular form of -2.7e^(√7) + 4.3e^(√5) is approximately -6.488 - 0.166i.

To express the complex numbers in polar form, we need to calculate the magnitude and the angle. The magnitude can be determined by calculating the square root of the sum of the squares of the real and imaginary parts. The angle can be found using the inverse tangent function (tan^(-1)) of the imaginary part divided by the real part.

Upon calculating the magnitude and the angle, we obtain the polar form of -2.7e^(√7) + 4.3e^(√5) as approximately 6.494 ∠ -176.14°.

Learn more about complex number

brainly.com/question/20566728

#SPJ11

For 500 people, 16 bags are needed to provide food.

Given data,

For a feast, you must buy chicken cutlets. Each visitor will receive 5 ounces of each cutlet, which weighs 10 ounces. The culets are packaged in 10-pound containers frozen.

For 500 people, how many bags will you need to order?

Now,

1 pound = 16 ounces

10 pounds = 160 ounces

160x ≥ 500x5

160x ≥ 2500

x ≥ 2500/160

x ≅ 16

Hence, 16 bags are needed in order to feed 500 guests.

To learn more about pounds click here:

brainly.com/question/27994061

#SPJ4

that is the circumference of its circular base.

\(\textit{volume of a cone}\\\\ V=\cfrac{\pi r^2 h}{3}~~ \begin{cases} r=radius\\ h=height\\[-0.5em] \hrulefill\\ h=9\\ V=27\pi \end{cases}\implies 27\pi =\cfrac{\pi r^2 (9)}{3}\implies 27\pi =3\pi r^2 \\\\\\ \cfrac{27\pi }{3\pi }=r^2\implies 9=r^2\implies \sqrt{9}=r\implies \underline{3=r} \\\\[-0.35em] ~\dotfill\\\\ \textit{circumference of a circle}\\\\ C=2\pi r\qquad \qquad \qquad C=2\pi (\underline{3})\implies C=6\pi\)

The circumference of the cone will be;

⇒ 6π

Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.

Given that;

The volume of a right cone = 27π units³

And, The height = 9 units

Now,

Since, We know that;

The volume of cone = πr²h / 3

⇒ 27π = π × r² × 9 / 3

⇒ 27 = r² × 3

⇒ r² = 27/3

⇒ r² = 9

⇒ r = 3

Since, The circumference of the cone = 2πr

                                                            = 2 × π × 3

                                                            = 6π

Learn more about the mathematical expression visit:

brainly.com/question/1859113

#SPJ2

Answer: 40 kilometers

Step-by-step explanation: Since the word ratio is cm/km (centimeter/kilometer), and the number ratio is 2/5, you will have to create another set and put the 16 cm next to the 2 cm. So it would be 2/5=16/X. Now you have to find the value of x. First, you have to multiply 5 by 16, which is equal to 80. Now you divide it by 2 and you will get 40 kilometers as your final answer.

There isn't enough evidence to indicate that the percentage of Americans who own American-made cars is more than 53 percent.

A representative of a car manufacturer in the United States claimed that 53 percent of Americans owned American-made cars ten years ago.

However, today, the percentage is higher.

A research group conducted a study to find out whether the statement was true.

They found out that 56 percent of a random sample of car owners in the United States owned American-made cars. The appropriate hypothesis test produced a p-value of 0.283.

Assuming the conditions for inference were satisfied, is there sufficient evidence to conclude, at the level of significance of α = 0.05

At α = 0.05, we want to see if there is enough evidence to reject the null hypothesis.

Therefore, since α = 0.05, the null hypothesis (H0) should be tested against the alternative hypothesis (Ha).

H0: μ ≤ 0.53 (The percentage of Americans who own American-made cars is no higher than 53%).

Ha: μ > 0.53 (The percentage of Americans who own American-made cars is higher than 53%).

It is clear that the researcher's claim was not supported by the evidence since the p-value of 0.283 was far above the significance level of α = 0.05.

Therefore, there is no statistically significant evidence to reject the null hypothesis (H0).

The research group discovered that 56 percent of a randomly selected sample of car owners in the United States owned American-made cars.

The null hypothesis states that the percentage of Americans who own American-made cars is no higher than 53 percent.

Since the p-value was greater than 0.05, we failed to reject the null hypothesis.

For similar question on percentage.

https://brainly.com/question/24304697

#SPJ11

(a) The doubling time of the population is approximately 13.86 years., (b) It takes approximately 23.10 years for the population to triple in size, (c) It takes approximately 27.72 years for the population to quadruple in size.

To calculate the doubling time of the population, we need to find the time it takes for the population to double from its initial value. In this case, the initial population is 9 million.

(a) Doubling Time:

Let's set up an equation to find the doubling time. We know that when the population doubles, it will be 2 times the initial population.

2P(0) = P(t)

Substituting P(t) = 9e^(0.05t), we have:

2 * 9 = 9e^(0.05t)

Dividing both sides by 9:

2 = e^(0.05t)

To solve for t, we take the natural logarithm (ln) of both sides:

ln(2) = 0.05t

Now, we can isolate t by dividing both sides by 0.05:

t = ln(2) / 0.05

Using a calculator, we find:

t ≈ 13.86

Therefore, the doubling time of the population is approximately 13.86 years.

(b) Time to Triple the Population:

Similar to the doubling time, we need to find the time it takes for the population to triple from its initial value.

3P(0) = P(t)

3 * 9 = 9e^(0.05t)

Dividing both sides by 9:

3 = e^(0.05t)

Taking the natural logarithm of both sides:

ln(3) = 0.05t

Isolating t:

t = ln(3) / 0.05

Using a calculator, we find:

t ≈ 23.10

Therefore, it takes approximately 23.10 years for the population to triple in size.

(c) Time to Quadruple the Population:

Similarly, we need to find the time it takes for the population to quadruple from its initial value.

4P(0) = P(t)

4 * 9 = 9e^(0.05t)

Dividing both sides by 9:

4 = e^(0.05t)

Taking the natural logarithm of both sides:

ln(4) = 0.05t

Isolating t:

t = ln(4) / 0.05

Using a calculator, we find:

t ≈ 27.72

Therefore, it takes approximately 27.72 years for the population to quadruple in size.

Learn more about logarithm at: brainly.com/question/30226560

#SPJ11

Answer:

D. About 9.4 units

Step-by-step explanation:

\(ab = \sqrt{ {(9 - 4)}^{2} + {(10 - 2)}^{2} } \\ ab = \sqrt{ {(5)}^{2} + {(8)}^{2} } \\ ab = \sqrt{25 + 64} \\ ab = \sqrt{89} \\ ab = 9.43398 \: units\)

Answer:

9 value is ====*0.9*

can you friendship with me i am Indian boy

The only correct fact about the F-statistic is:

The F-statistic has 3 degrees of freedom in the numerator and 54 degrees of freedom in the denominator.

From the given information, the doctors used a one-way ANOVA F-test to analyze the change in body fat percentage data for the four exercise regimens. They calculated the mean square due to treatment as MST = 18.878621 and the mean square for error as MSE = 1.297963.

To determine the correct facts about the F-statistic for this test, we can use the formula for the F-statistic:

F = MST / MSE

Substituting the given values, we get:

F = 18.878621 / 1.297963 ≈ 14.5448

So, the correct facts about the F-statistic are:

The F-statistic has 3 degrees of freedom in the numerator (number of treatment groups - 1) and 54 degrees of freedom in the denominator (total sample size - number of treatment groups).

The F-statistic indicates whether there are significant differences among the treatment groups based on the change in body fat percentage data.

The F-statistic is not 0.0688 or any other value besides 14.5448, based on the calculation using the given MST and MSE values.

The F-statistic increases as the differences among the sample means for the exercise groups increase.

Therefore, the only correct fact about the F-statistic is:

The F-statistic has 3 degrees of freedom in the numerator and 54 degrees of freedom in the denominator.

To know more about degrees of freedom refer here:

https://brainly.com/question/31424137

#SPJ11

Answer:

23 cm, 25 cm

Step-by-step explanation:

Let the Width be W cm.

Since the Length and Width are consecutive odd integers we know that the length:

Length = (W + 2) cm

Perimeter of Rectangle = Sum of all sides = 2 x Length + 2 x Width

So rewriting the perimeter , we have:

2W + 2(W+2) = 96 cm

Now lets solve for W to get the width.

2W + 2W + 4 = 96 cm

4W + 4 - 4 = 96 - 4

4W = 92 cm

W = 23 cm

Next, we know that the length = (W + 2) cm

Therefore the length = 23 + 2 = 25 cm

Answer:

You can buy 1/4 pound of blueberries for $1.00

You can also buy 3 1/4 pounds of blueberries for $13.00

Answer:

For A the answer is 0 for B the answer is 3.25

Step-by-step explanation:

A: a is 0 because it says blueberries cost 4.00 per pound so a is asking how many pounds can we buy with 1.00 and since one pound is 4.00 then you cant buy any pounds of berries with 1.00

B: B is 3.25 but to get a whole number answer round 3.25 to get 3.3 (which is the closet to a whole number we can get)

Answer:

B: isosceles

Step-by-step explanation:

Two angles of an isosceles acute triangle measure the same.

The coordinates of the center is (32, 40.5).

length of the radius of the circle is 73 units.

The coordinates of the center is solved using the formula for midpoints expressed as

Midpoint x-coordinate = (x₁ + x₂) / 2

Midpoint y-coordinate = (y₁ + y₂) / 2

Plugging in the values:

x₁ = 8 and y₁ = 13

x₂ = 56 and y₂ =68

Midpoint x-coordinate

= (8 + 56) /2

= 64/2

= 32

Midpoint y-coordinate

= (13 + 68) /2

= 81/ 2

= 40.5

distance formula will be used to find the length of the radius of the circle

d = √[(x₂ - x₁)² + (y₂ - y₁)²]

Plugging in the values:

= √[(56 - 8)² + (68 - 13)²]

= √(48² + 55²)

= √(2304 + 3025)

= √5329

= 73

Learn more about circle at

https://brainly.com/question/24375372

#SPJ1

Step-by-step explanation:

the correct answer is option a 6a-7

Step-by-step explanation:    Hello There!

When we are given two side lengths and the included angle we use this formula to solve for the area

A = 1/2absin(C)

where a and b = the side lengths and c = the included angle

The triangle gives us the following information

side length - 10 ft

side length - 4 ft

included angle - 37

Given this information we plug it into the formula

A = 1/2 4 * 10sin(37)

10 * 4 = 40

40sin(37) = 24.07260093  

24.07260093  = 12.03630046

Finally we round to the nearest tenth and get that the area of the triangle is 12ft²

Answer:

5 + 2s

Step-by-step explanation:

To simplify this expression, we will simply factor out the variable s from the terms with s, and use addition and the distributive property to reapply the variable to the simplified term.

5 + 10s - 8s

= 5 + s ( 10 - 8 )

= 5 + s ( 2 )

= 5 + 2s

Hence, the simplified expression of 5 + 10s - 8s is 5 + 2s.

Cheers.

Answer:

A

Step-by-step explanation:

The area (A) of the sector is calculated as

A = area of circle × fraction of circle

    = πr² × \(\frac{150}{360}\)

    = π × 12² × \(\frac{15}{36}\)

    = 144π × \(\frac{5}{12}\) ( cancel 144 and 12 by 12 )

    = 12π × 5

    = 60π

     ≈ 188.5 Km² ( to the nearest tenth ) → A

a) The null space of A is a subspace of the 7-dimensional vector space R^7, and its dimension is 3.

b) The column space of A is a subspace of the 5-dimensional vector space R^5.

The null space of a matrix is the subspace of the vector space in which the matrix operates. In this case, since A is a 5x7 matrix, its null space is a subspace of the 7-dimensional vector space R^7.

a) The dimension of the null space can be found using the rank-nullity theorem, which states that the dimension of the null space plus the rank of the matrix equals the number of columns. Since the rank of A is 4 and it has 7 columns, we have:

dim(null space) + rank(A) = number of columns

dim(null space) + 4 = 7

dim(null space) = 3

Therefore, the null space of A is a subspace of R^7 with dimension 3.

b) The column space of a matrix is the subspace of the vector space generated by the columns of the matrix. In this case, since A is a 5x7 matrix, its column space is a subspace of the 5-dimensional vector space R^5. This is because the columns of A are vectors in R^5. Therefore, the column space of A is a subspace of R^5.

Learn more about column space here

brainly.com/question/29894379

#SPJ4

The value of the given line integral ∫cxydx+(x−y)dywhen C consists of line segments from (0,0) to (3,0) and from (3,0) to (4,2) is 23/2.

We can evaluate the line integral by breaking it up into two parts along the two line segments of the curve:

∫cxydx+(x−y)dy = ∫C1xydx+(x−y)dy + ∫C2xydx+(x−y)dy

where C1 is the line segment from (0,0) to (3,0) and C2 is the line segment from (3,0) to (4,2).

Along C1, y = 0, so the integral reduces to:

∫C1xydx+(x−y)dy = ∫₀³ x(0)dx + (x - 0)dy = ∫₀³ xdx = [x²/2]₀³ = 9/2

Along C2, we can parameterize the curve as x = 3t, y = 2t for 0 ≤ t ≤ 1, so dx = 3dt and dy = 2dt. Substituting these into the integral, we get:

∫C2xydx+(x−y)dy = ∫0¹ (3t)(2t)(3dt) + (3t - 2t)(2dt)

= ∫₀¹ (18t² + 2t)dt = [6t³ + t²]₀¹ = 7

Thus, the line integral over the entire curve C is:

I = ∫C1xydx+(x−y)dy + ∫C2xydx+(x−y)dy = 9/2 + 7 = 23/2.

Therefore, the value of the given line integral is 23/2.

Learn more about the integral at https://brainly.com/question/31039100

#SPJ11

If st - sv, m∠sut - w + °10, and m∠suv =3w, the measure of angle SUT is 52.5°.

Given the information provided, we can set up the following equations:

1) m∠SUT + m∠SUV = 180° (since they are supplementary angles)
2) m∠SUT = w + 10°
3) m∠SUV = 3w

Now we can substitute equations (2) and (3) into equation (1):

(w + 10°) + (3w) = 180°

Combining like terms, we get:

4w + 10° = 180°

Now, subtract 10° from both sides:

4w = 170°

Finally, divide both sides by 4:

w = 42.5°

Now we can find m∠SUT by substituting the value of w back into equation (2):

m∠SUT = 42.5° + 10°

m∠SUT = 52.5°

So, the measure of angle SUT is 52.5°.

More on angles: https://brainly.com/question/10644397

#SPJ11

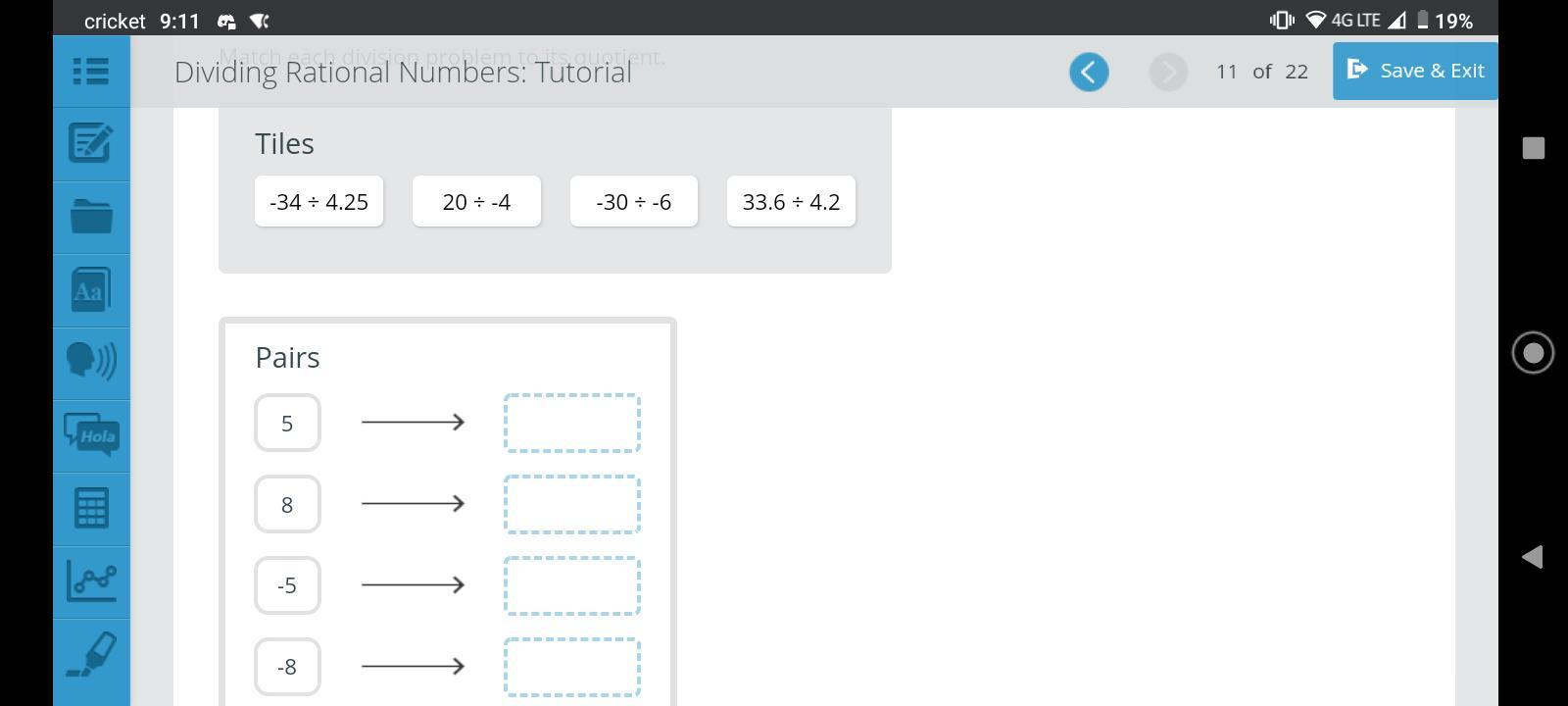
Answer:

Step-by-step explanation:

5= -33÷-6

8= 33.6÷4.2

-5= 20÷-4

-7= -34÷4.25

The approximate surface-area-to-volume ratio of a bowling ball with a radius of 5 inches is 0.6

To find the approximate surface-area-to-volume ratio of a bowling ball with a radius of 5 inches, we will first calculate the surface area (SA) and volume (V) of the ball, and then divide the surface area by the volume.

Step 1: Calculate the surface area (SA) using the formula for the surface area of a sphere:

\(SA = 4 πr^2\)
\(SA = 4 π5^2\)
\(SA = 4 π(25)\)
\(SA=100π\)

Step 2: Calculate the volume (V) using the formula for the volume of a sphere:

\(V = \frac{4}{3} π (r)^{3}\)
\(V = \frac{4}{3} π (5)^{3}\)
\(V = \frac{4}{3} π (125)\)
V = 166.67 π cubic inches

Step 3: Calculate the surface-area-to-volume ratio (SA/V)
\(\frac{SA}{V} = \frac{100}{166.67}\)
\(\frac{SA}{V}=\frac{100}{166.67}\)

\(\frac{SA}{V}= 0.6\)

So the approximate surface-area-to-volume ratio of a bowling ball with a radius of 5 inches is 0.6. The best answer from the choices provided is A.

To know more about "volume of a sphere" refer here:

https://brainly.com/question/30522025#

#SPJ11

To find the profit function, maximum profit quantity, and maximum profit for a firm with revenue\(R(q) = 15q - 0.5q^2\) and cost \(C(q) = q^3 - 13.5q^2\\\) + 50q + 40, we first subtract the cost from the revenue to obtain the profit function \(\prod(q) = R(q) - C(q)\). Then, we can determine the quantity where the profit is maximized by using the second derivative test. Finally, we can calculate the maximum profit by substituting the quantity found in part (b) into the profit function \(\prod(q)\).

a. The profit function \(\prod(q)\) is obtained by subtracting the cost function C(q) from the revenue function R(q). Therefore, \(\prod(q) = R(q) - C(q)\) =\((15q - 0.5q^2) - (q^3 - 13.5q^2 + 50q + 40\)). Simplifying this expression gives \(\prod(q)\) = \(-q^3 + 14q^2 - 35q - 40\).

b. To determine the quantity where the profit is maximized, we can use the second derivative test. The second derivative of the profit function \(\prod(q)\) is obtained by differentiating \(\prod(q)\) with respect to q twice. Taking the second derivative of \(\prod(q)\), we get \(\prod''(q) = -6q + 28\). To find the quantity where the profit is maximized, we set \(\prod''(q)\) equal to zero and solve for q: -6q + 28 = 0. Solving this equation gives q = 28/6 = 14/3.

c. Once we have found the quantity q = 14/3, we can substitute this value into the profit function Π(q) to find the maximum profit. Plugging q = 14/3 into \(\prod(q)\), we have \(\prod(14/3) = -(14/3)^3 + 14(14/3)^2 - 35(14/3) - 40\). Evaluating this expression gives the maximum profit value.

\(\prod(14/3) = -((14/3)^3) + 14((14/3)^2) - 35(14/3) - 40.\)

Simplifying this expression gives:

\(\prod(14/3) = -2744/27 + 2744/9 - 490/3 - 40.\)

Combining the terms and finding a common denominator:

\(\prod(14/3) = (-2744 + 8192 - 4410 - 1080)/27.\)

Further simplification:

\(\prod(14/3) = 958/27.\)

Therefore, the maximum profit at the quantity q = 14/3 is 958/27.

Learn more about second derivative test here:

https://brainly.com/question/30404403

#SPJ11

The probability that they will run out of raw material is 0.78 or 78% if the order quantity is 150 gallons.

We have following information,

the demand for the polymer is distributed normally .

Mean (μ) = 250 gallons and Standard deviations (σ) = 125 gallons

Selling price of poymer = $25 per gallons

cost price of raw material for polymer= $ 10 per gallons

Salvage value = $(-5)/ gallon

Now, Using the formula for normally distributed sample,

Z = ( X - μ ) /σ

where , X---> sample mean

μ ----> population mean

σ----> standard deviations

Z -----> Z-value

from question it is clear X = 150

putting all the values of variables in above formula we get, Z = ( 150-250)/125 = -100/125

= - 0.8

(-0.8) value of z = 0.21 = 21% , the value of z is measure from normal distribution table.

They will run out of raw material if demands exceds this quantity or

Probability ( out of stock ) = 1 - 0.21 = 0.79 = 79%

So, the probability that they will run out of raw material is 0.78 or 78% if the order quantity is 150 gallons.

To learn more about Normal distribution , refer:

https://brainly.com/question/4079902?utm

# SPJ4

#Complete Question :

Goop Inc needs to order a raw material to make a special polymer. The demand for the polymer is forecasted to be Normally distributed with a mean of 250 gallons and a standard deviation of 125 gallons. Goop sells the polymer for $25 per gallon. Goop's purchases raw material for $10 per gallon and Goop mrust spend $5 per gallon to dispose off all unused raw material due to government regulations. (One gallon of raw material yields one gallon of polymer.) That is to say, the salvage value is $(-5)/gallon. If demand is more than Goop can make, then Goop sells only what they made and the rest of demand is lost. ?

1. Suppose Good purchases 150 gallons of raw material. What is the probability that they will run out of raw material? ?

The value of 'x' in the hexagon measures 88°.

A polygon is a closed more than two-sided and can be made up of a finite number of straight line segments and is a type of planar figure in geometry.

Each line of the polygonal circuit's segments is referred to as its edges or sides.

We know, A hexagon has 6 sides and it has 6 interior angles.

We also know that the sum of all the interior angles in a hexagon is 720°.

Therefore, From the given information,

(120° + 95° + 120° + 125° + x + 172°) = 720°.

x + 632° = 720°.

x = (720 - 632)°.

x = 88°.

learn more about polygons here :

https://brainly.com/question/24464711

#SPJ1

If the estimate of the population standard deviation is 8, the sample size is 62

In this question, you want to estimate the population mean with 95% confidence with a margin of error of 2.

if the estimate of the population standard deviation is 8, we need to find the sample size.

here, α = (1 - 0.95)/2

         α = 0.025

Now, we have to find z in the Ztable as such z has a pvalue of 1 - α

so, z = 1.96

Now, to find the margin of error M we have formula

M = z * σ/√n

2 = 1.96 * 8/√n

√n = 1.96 * 4

√n = 7.84

n = 61.47

n ≈ 62

Therefore,  if the estimate of the population standard deviation is 8, the sample size is 62

Learn more about the sample size here:

https://brainly.com/question/17039768

#SPJ4

A definite integral is said to be improper if one or both of the limits of integration are infinite, or if the integrand function has a vertical asymptote within the interval of integration.

In other words, an improper integral is one that cannot be evaluated using the usual techniques of integration, such as the fundamental theorem of calculus, because it involves infinite limits or a function that is not integrable over the interval.

For example, the definite integral of f(x) = 1/x from 1 to infinity is an improper integral because the upper limit of integration is infinity, which is not a finite number. Similarly, the definite integral of f(x) = ln(x) from 0 to 1 is an improper integral because the lower limit of integration is 0, and the function has a vertical asymptote at x=0.

To evaluate improper integrals, we use limit processes to determine whether the integral converges (has a finite value) or diverges (has an infinite value). If the integral converges, we can find its value by taking the limit of a related integral as one or both of the limits of integration approach infinity or zero.

To learn more about Definite integral :

https://brainly.com/question/30074848

#SPJ4

Answer:

Step-by-step explanation:

Arc length=∅/360×2πr (can't find the symbol of theta, use ∅ instead LOL)

\(\frac{\theta }{360}\cdot 2\pi \left(11\right)=16\)

\(\frac{\theta }{360}=\frac{16}{22\pi }\)

\(\theta \:=\frac{16}{22\pi \:}\cdot 360\)

\({\theta}=83.34\)

Answer:

≈ 1.5 radians

Step-by-step explanation:

The arc length is calculated as

arc = circumference of circle × fraction of circle

Here arc = 16 , then

2πr × \(\frac{0}{2\pi }\) = 16 ← cancel the 2π on numerator/denominator

11 ×θ = 16 ( divide both sides by 11 )

θ ≈ 1.5 radians ( to the nearest tenth )