138 130 135 140 120 125 120 130 130 144 143 140 130 150 The mean (x) for the following ungrouped data distribution to its right is: a. 1.24 b. 2.01 c. 2:18 a.m. 2.45 The arithmetic mean of the sample is: a. 130 b. 132.5 c133.93 d. 9.0423
Answers
The mean (x) of the ungrouped data distribution is approximately 134.29. The arithmetic mean of the sample is approximately 133.93.
The mean (x) for the given ungrouped data distribution is calculated by summing up all the values and dividing by the total number of values. In this case, the sum of the values is 1880 and there are 14 values. Therefore, the mean is 1880 divided by 14, which is approximately 134.29.
The arithmetic mean of the sample is the same as the mean of the ungrouped data distribution, which is approximately 134.29. Therefore, the correct option is (c) 133.93.
So, the mean (x) for the ungrouped data distribution is approximately 134.29, and the arithmetic mean of the sample is approximately 133.93.
To learn more about “distribution” refer to the https://brainly.com/question/4079902
#SPJ11
Related Questions
Prove that the gcd operator is associative on Z+. That is, show that for all a, b, c € Z+, gcd(a, gcd(b, c)) = gcd(gcd(a, b), c).
Answers
To prove that the gcd operator is associative on Z+ (the set of positive integers), we need to show that for any positive integers a, b, and c, the equation gcd(a, gcd(b, c)) = gcd(gcd(a, b), c) holds true.
Let's start by considering the left-hand side (LHS) of the equation:
LHS: gcd(a, gcd(b, c))
Using the definition of gcd, we know that gcd(b, c) divides both b and c, and any common divisor of b and c must also divide gcd(b, c). Therefore, gcd(a, gcd(b, c)) must divide a and gcd(b, c).
Now, let's consider the right-hand side (RHS) of the equation:
RHS: gcd(gcd(a, b), c)
Again, using the definition of gcd, we know that gcd(a, b) divides both a and b, and any common divisor of a and b must also divide gcd(a, b). Therefore, gcd(gcd(a, b), c) must divide gcd(a, b) and c.
To prove the associativity of the gcd operator, we need to show that both sides of the equation have the same divisors.
Let d be any positive integer that divides both gcd(a, gcd(b, c)) and gcd(gcd(a, b), c). We need to show that d divides both a and c.
Since d divides gcd(a, gcd(b, c)), it must divide a and gcd(b, c).
Similarly, since d divides gcd(gcd(a, b), c), it must divide gcd(a, b) and c.
Combining these two facts, we can conclude that d must divide a, b, and c.
Therefore, any positive integer that divides both sides of the equation must divide a, b, and c.
Hence, we have proved that gcd(a, gcd(b, c)) = gcd(gcd(a, b), c) for all positive integers a, b, and c.
This shows that the gcd operator is associative on Z+.
To learn more about common divisor visit:
brainly.com/question/27962046
#SPJ11
Which of the following BEST describes the following differential equation y x²y² = x² ? - (C) Nonlinear and separable (A) Linear and separable (B) Linear and not separable (D) Nonlinear and not separable O(A) (B) (C) (D)
Answers
The given differential equation y x²y² = x² is a nonlinear and not separable differential equation, which corresponds to option (D).
A linear differential equation can be written in the form dy/dx + P(x)y = Q(x), where P(x) and Q(x) are functions of x. In this equation, the term x²y² makes it nonlinear.
A separable differential equation can be written in the form g(y)dy = f(x)dx, where g(y) and f(x) are functions of y and x, respectively. However, in the given equation, we cannot separate the variables y and x to obtain such a form.
To solve this particular differential equation, one approach is to rewrite it in a more manageable form. Let's rearrange the terms:
x² = y/(x²y²)
Now, we can multiply both sides by (x²y²) to eliminate the denominator:
x²(x²y²) = y
This equation is still nonlinear but can be used to find a particular solution for y given a specific initial condition.
To know more about nonlinear and separable differential equations, refer here:
https://brainly.com/question/30466149#
#SPJ11
Simply the expression.
4 (2m -6) - 3p - 2m + 8

Answers
Let's solve the equation.
4 (2m -6) - 3p - 2m + 8
= 8m - 24 - 3p - 2m + 8 (We simplified 4 (2m -6))
= 6m - 16 - 3p (We added the 8 to the 24)
= 6m - 3p - 16 (We organized the variables together so it matches an answer.)
The answer is A!
Answer: hii
The answer; 6m - 3p -16Step-by-step explanation:
How to solve your problem:
4 (2m -6) - 3p - 2m + 8
Simplify.
Distribute.
4 (2m -6) - 3p - 2m + 8
8m - 24 - 3p - 2m + 8
Add the numbers:
8m - 24 - 3p - 2m + 8
8m - 16 - 3p - 2m
Combine like terms:
8m - 16 - 3p - 2m
6m - 16 - 3p
Rearrange terms:
6m - 16 - 3p
6m - 3p - 16
Solution:
6m - 3p -16
Hopefully this helps you ~
- Matthew
Let f(x) = (x+5) sin(5x).
We will find the degree 3 Taylor polynomial for f(x) at x=0.
First we calculate all the things we need, you can check your answers as you go.
f(0) f'(x)=
f'(0) =
f" (x)=
f"(0) = = Number
f(x) =
Answers
The degree 3 Taylor polynomial for the function f(x) = (x+5)sin(5x) at x=0 . The degree 3 Taylor polynomial for f(x) at x=0 is \(P(x) = 0 + 25x + (5/2)x^2 + (f"'(0)/3!)x^3.\)
To find the degree 3 Taylor polynomial for f(x) at x=0, we need to calculate the function and its derivatives.
First, let's find f(0). Plugging x=0 into the function f(x) = (x+5)sin(5x), we have f(0) = (0+5)sin(5(0)) = 0.
Next, we find f'(x) by taking the derivative of f(x) with respect to x. Using the product rule and the chain rule, we get f'(x) = (1)(sin(5x)) + (x+5)(5cos(5x)) = sin(5x) + 5(x+5)cos(5x).
Evaluating f'(x) at x=0 gives us f'(0) = sin(0) + 5(0+5)cos(0) = 0 + 5(5)(1) = 25.
Taking the second derivative, f"(x), we differentiate f'(x) with respect to x, which yields f"(x) = 5cos(5x) + 5(x+5)(-5sin(5x)).
Evaluating f"(x) at x=0 gives f"(0) = 5cos(0) + 5(0+5)(-5sin(0)) = 5 + 5(5)(0) = 5.
Now that we have the necessary values, we can construct the Taylor polynomial. The general form of a degree 3 Taylor polynomial is P(x) = f(0) + f'(0)x + (f"(0)/2!)x^2 + (f"'(0)/3!)x^3.
Substituting the values we calculated, the degree 3 Taylor polynomial for f(x) at x=0 is the degree 3 Taylor polynomial for f(x) at x=0 is \(P(x) = 0 + 25x + (5/2)x^2 + (f"'(0)/3!)x^3.\)
Learn more about function here:
https://brainly.com/question/30721594
#SPJ11
.2. Determine whether the feasible set for each of the following systems of constraints is convex, and if not, indicate points x^1 and x² that violate definition. a) (x1)² + (x2)² > 9
x1 + x2 ,10
x1, x2 > 0
Answers
The feasible set for this system of constraints is not convex, and the points (5, 5) and (3, 7) violate the convexity definition.
To determine whether the feasible set for each system of constraints is convex, we need to analyze the constraints individually and examine their intersection.
a) (x1)² + (x2)² > 9
This constraint represents points outside the circle with a radius of √9 = 3. The feasible set includes all points outside this circle.
b) x1 + x2 ≤ 10
This constraint represents points that lie on or below the line x1 + x2 = 10. The feasible set includes all points on or below this line.
c) x1, x2 > 0
This constraint represents points in the positive quadrant, where both x1 and x2 are greater than zero.
Now, let's analyze the intersection of these constraints:
Considering the first two constraints (a and b), we can see that the feasible set consists of all points outside the circle (constraint a) and below or on the line x1 + x2 = 10 (constraint b).
To determine whether the feasible set is convex, we need to check if any two points within the set create a line segment that lies entirely within the set.
If we consider the points (5, 5) and (3, 7), both points satisfy the individual constraints (a) and (b). However, the line segment connecting these two points, which is the line segment between (5, 5) and (3, 7), exits the feasible set since it passes through the circle (constraint a) and above the line x1 + x2 = 10 (constraint b).
Therefore, the feasible set for this system of constraints is not convex, and the points (5, 5) and (3, 7) violate the convexity definition.
Learn more about circle here
brainly.com/question/11878555
#SPJ4
Mason and Daisy are building towers. Each one of Masons blocks is 6cm tall. Each one of Daisys blocks is 8cm tall. They both build towers that are exactly the same height. What is the smallest height that their towers could be?Give your answer in cm
Answers
Reason:
GCF = greatest common factor
LCM = lowest common multiple
GCF of 6 and 8 = 2
LCM of 6 and 8 = (6*8)/GCF = (6*8)/2 = 48/2 = 24
We can list out the multiples of each to confirm this
multiples of 6 are: 6, 12, 18, 24, 30, ...multiples of 8 are: 8, 16, 24, 32, ...If Mason's tower is 24 cm tall, then he uses 24/6 = 4 blocks; while Daisy will use 24/8 = 3 blocks for her tower of the same height.
The smallest height that their towers could be 24 cm.
What is the lowest common factor?The lowest of two or more natural numbers' common multiples is referred to as the Lowest Common Multiple (LCM). The least Common Multiple and Least Common Divisor are other names for it (LCD). For instance, 12 is the least frequent multiple of 4 and 6.
GCF = greatest common factor
LCM = lowest common multiple
GCF of 6 and 8 = 2
LCM of 6 and 8 = (6*8)/GCF = (6*8)/2 = 48/2 = 24
We can list out the multiples of each to confirm this
multiples of 6 are 6, 12, 18, 24, 30, ...
multiples of 8 are: 8, 16, 24, 32, ...
If Mason's tower is 24 cm tall, then he uses 24/6 = 4 blocks; while Daisy will use 24/8 = 3 blocks for her tower of the same height.
To know more about the lowest common factor follow
https://brainly.com/question/10749076
#SPJ2
Please answer correctly !!!!! Will mark brainliest answer !!!!!!!!!!

Answers
Answer:
type 2 in the first box,
13/4 in the second box, and
-9/8 in the third one
Step-by-step explanation:Notice that you are asked to write the following quadratic expression in vertex form, so you need to find the "x" value of the vertex, and then the "y" value of the vertex:
\(x_{vertex}= -b/2a\)
Which in our case is: -13/4
and the value of the y for the vertex is obtained using the functional expression when x equals -13/4:
\(f(-13/4)= -9/8\)
Then your expression for this quadratic should be:
\(f(x)=2\,(x+\frac{13}{4} )^2+(-\frac{9}{8})\)
Then type 2 in the first box, 13/4 in the second box, and -9/8 in the third one
Identify the constant in the expression -2 + 6c + 3c
Answers
Answer:
-2
Step-by-step explanation:
The constant has only a number and no variable
-2 +6c +3c
-2 is the constant
6 is a coefficient for the variable term
3 is a coefficient for the variable term
-2
How
Simplify the equation\(\\ \sf\longmapsto -2+6c+3c\)
\(\\ \sf\longmapsto -2+(6+3)c\)
\(\\ \sf\longmapsto -2+9c\)
\(\\ \sf\longmapsto 9c-2\)
-2 is constantWhat's the missing side of this triangle

Answers
7^2+9^2=130
Sqrt(130)=11.4
Answer:
20.25inches
Step-by-step explanation:
Using the Pythagorean theorem,
h^2=7^2 +19^2
h^2=410
h=sqr 410=20.25inches
4856cm=_________m
I will mark as brainlist
Answers
Answer:
48.56 m
Step-by-step explanation:
1 cm = 0.01 m
Or, if you want to change from cm to m. simply divide the cm by 100.
Thus,
4856 cm ÷ 100 = 48.56 m
can someone help me please?

Answers
Answer:
(0,4) and (-4,0)
Step-by-step explanation:
is 63/20 equivalent to 4/9 divided by 5/7
Answers
Answer:
No
Step-by-step explanation:
4/9 divided by 5/7 is equal to 4/9 * 7/5 = 28/45. We can see that 63/20 is not equivalent to 28/45 as 28/45 is less than one and 63/20 is greater than one.
DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD. If the area of the parallelogram is 1470 cm2 , AB=35cm and AD=49cm, Find the length of BM and DL.
Answers
Answer:
BM = 30 cm, DL = 42 cm
Step-by-step explanation:
The area of the parallelogram = 1470 cm², AB = 35 cm, AD = 49 cm, DL and BM are the heights on sides AB and AD.
area of the parallelogram = base × height = AD × height of AD = AD × BM
⇒ 1470 cm² = 49 cm × BM
BM = 1470 cm² / 49 cm = 30 cm
BM = 30 cm
Also:
area of the parallelogram = base × height = AB × height of AB = AB × DL
⇒ 1470 cm² = 35 cm × DL
DL = 1470 cm² / 35 cm = 42 cm
DL = 42 cm
Which number sentence is true?

Answers
Answer:
B
Step-by-step explanation:
Edge 2021.
7 (3 - 0.5k) 3k - 5
Answers
Step-by-step explanation:
63k -10.5k square 2-5 and you have you answer
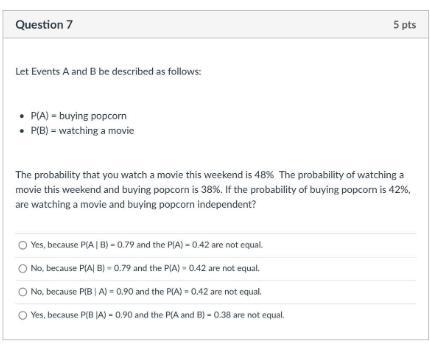
the probability that you watch a movie this weekend is 48% the probability of watching a movie this weekend and buying popcorn is 38%. if the probability of buying popcorn is 42%, are watching a movie and buying popcorn independent?
Answers
No, because P(A|B) = 0.79 and the P(A) = 0.48 they are not equal.
Probability :The probability formula defines the likelihood of the happening of an event. It is the ratio of favorable outcomes to the total favorable outcomes.
We have the information:
P(A)= 0.48
P(B) = 0.42
P(A∩B) = 0.38
To find out if watching a movie and buying a popcorn are independent,
The formula is used:
P(A|B) = P(A∩B)/P(A)
Plug all the values in above formula:
P(A|B) = 0.38/0.48 = 0.79166
P(A|B) = 0.79
From the deductions above;
Hence, the answer is
No, because P(A|B) = 0.79 and the P(A) = 0.48 they are not equal.
Learn more about Probability at:
https://brainly.com/question/30034780
#SPJ4
For complete question, to see the attachment
Write a formula that expresses the radius of the circle, r (in cm), in terms of the number of seconds, t , since the circle started shrinking.
Answers
The formula expressing the radius of the circle, r (in cm), in terms of the number of seconds, t, since the circle started shrinking is r = r₀ - kt, where r₀ is the initial radius and k is the rate at which the circle is shrinking.
The formula r = r₀ - kt represents the relationship between the radius of the circle and the time elapsed since it started shrinking. Here's an explanation of the variables:
r represents the radius of the circle at any given time t.r₀ represents the initial radius of the circle when it started shrinking .k represents the rate at which the circle is shrinking, indicating how much the radius decreases per unit of time.t represents the number of seconds that have elapsed since the circle started shrinking.
By subtracting kt from the initial radius r₀, we can determine the current radius of the circle at any given time t. The term kt represents the amount by which the radius decreases over time, based on the rate of shrinkage defined by the value of k.
To learn more about expressing.
Click here:brainly.com/question/1859113
#SPJ11
What is the constant of porportionality in the equation y=10;x=2
Answers
Answer:
x=2 and y=10
Step-by-step explanation:
Answer:
x = 2 and y = 10
Step-by-step explanation:
OMG FOR A BRAINLIST HELP ANSWER!!!!!!!!!

Answers
Answer:
C is answer
Step-by-step explanation:
good afternoon can someone please helppp :))))
Triangle XYZ is dilated by a scale factor of 1/4 to form triangle X'Y'Z'. Side YZ measures 18. What is the measure of side Y'Z'?
(Round your answer to the nearest tenth)

Answers
The height of a building is 72 m. Find the angle of elevation from a point on ground level that is 55 m away from the base of the building
Answers
Answer:
52.6 degrees
Step-by-step explanation:
tan^-1(72/55)
Angle of elevation is equals to 52°7'(approximately).
What is angle of elevation?
" Angle of elevation is the angle between the horizontal plane and line of sight from the point of observation."
Formula used
In a right angled triangle,
tanθ = ( opposite side) / adjacent side)
According to the question,
As shown in diagram
Height of the building (AB) = 72m
Distance between base of the building and point of observation
(BC)= 55m
Angle of elevation = θ
Substitute the value in the formula we have,
tanθ = AB / BC
= 72 / 55
⇒ θ = tan⁻¹ (72 /55)
= tan ⁻¹(1.3091)
= 52° 7' (approximately)
Hence, angle of elevation is equals to 52°7'(approximately).
Learn more about angle of elevation here
https://brainly.com/question/21137209
#SPJ2

The radioactive substance cesium-137 has a half-life of 30 years. The amount A(t) (in grams) of a sample of cesium -137 remaining after t years is given by the following exponential function.A (t) = 523 (1/2)^t/30Find the initial amount in the sample and the amount remaining after 100 years.Round your answers to the nearest gram as necessary.Initial amount:Amount after 100 years:
Answers
After 100 years:
Replace t by 100:
A (t) = 523 (1/2)^t/30
A (100) = 523 (1/2)^100/30 = 523 (1/2) ^10/3 = 51.88 =52 grams
The initial amount of the sample is 523
A furniture store sells kits that customers use to build cabinets. Each kit contains 18 screws and a set number of boards.
Jarred buys 6 of these kits and has a total of 192 screws and boards. The equation shown represents this situation.
6(x + 18) = 192
What does the variable x represent in Jarred's equation?
A)the number of screws in all 6 kits
B)the number of screws in one kit
C)the number of boards in all 6 kits
D)the number of boards in one kit
Answers
Step-by-step explanation: A) and B) wouldn’t make sense to the given question (process of elimination)
So C) or D) welp D is only talking about one kit when there’s 6 kits so D cannot be the answer
So the answer is C)
Please mark me as brainliest
Have a nice day!
Answer:
C or D cause A B doesnt make sence its d
Step-by-step explanation:
Use an Addition or Subtraction Formula to write the expression as a trigonometric function of one number. cos 13π 15 cos − π 5 − sin 13π 15 sin − π 5 Find its exact value.
Answers
As per the addition formula, the value of the trigonometric function is -0.809.
In statistics, function is defined as a relationship between inputs where each input is related to exactly one output.
Here we have to find the value of the trigonometric function cos(13/15)cos(-/5)-sin(13/15)sin(-/5) by using the addition and subtraction formula.
Here we have the following trigonometric function:
=> cos(13/15)cos(-/5)-sin(13/15)sin(-/5)
Now, we have to use the trigonometric addition formula,
=> Cos (A+B) = Cos A Cos B - Sin A Sin B
To solve the given function,
Here let us rewrite the given function based on the addition formula, then we get,
=> Cos ( 13π/15 + (-π/5) )
=> Cos( 12π/5)
=> Cos(144°)
=> -0.809
To know more about function here.
https://brainly.com/question/10354322
#SPJ4
a 32-ounce package of snack mix is 24 percent pretzels. how many ounces are pretzels
Answers
If 24 percent of the snack mix is pretzel, we simply need to multiply the total number of ounces by 0.24.
0.24 x 32 = 7.68
7.68 ounces of the snack mix will be pretzels.
Answer:
answer is D.
you multiply 32 x .24 = 7.68oz
Step-by-step explanation:
the way you solve this question
32 x .24%= 7.68 oz
make sure you place your decimal place to spaces to your left!
hope this helps!
90° 20" - 78° 45' 30"
Quick pls
Answers
Neeeeddd helllp again again

Answers
Answer:
A
Step-by-step explanation:
3.5 + p = 7.5
Subtract from 3.5 from both sides.
p = 7.5 - 3.5
Simplify
p = 4
A is the number line that has the correct answer.
Using the z table, determine the critical value for the left-tailed test with α = 0.02. Round your answer to 2 decimal places.
Answers
-2.05 is the critical value for the left-tailed test .
What is critical z value?
The -1.96 and +1.96 standard deviations are the essential z-score values when adopting a 95 percent confidence level.
With a 95 percent confidence level, the uncorrected p-value is equal to 0.05.The critical value for a two-sided test is Z 1-/2, while for a one-sided test, it is Z 1.
You reject the null hypothesis if the absolute Z-value is higher than the crucial value. If not, you have not successfully ruled out the null hypothesis.
Given that,
α = 0.02.
left tailed test
Zα = 0.02 = -2.05
critical value = -2.05
Learn more about critical z value
brainly.com/question/29692242
#SPJ1
In the game of Roulette, if you place a $10 bet on number 12, there are two possible outcomes:
either you profit $350, or you lose $10. (The prize is $360 but subtracting the $10 bet equals a net gain of
$350). The probability that you win is 1
38
and the probability that you lose is
37
38
.
a. Calculate the expected value of how much money you’ll get if you bet $10 on number 12 in Roulette.
Show full work to receive credit.
b. Based on your expected value from part a, is it a good idea to play Roulette over and over again? Give
a mathematical explanation for your answer.
Answers
a. To calculate the expected value of how much money you’ll get if you bet $10 on number 12 in Roulette, we can use the formula: Expected Value = (Probability of Winning * Amount Won) - (Probability of Losing * Amount Lost)
In this case, the probability of winning is 1/38, and the amount won is $350. The probability of losing is 37/38, and the amount lost is $10. Substituting these values into the formula, we get: Expected Value = (1/38 * $350) - (37/38 * $10)
Expected Value = $9.21 Therefore, the expected value of how much money you’ll get if you bet $10 on number 12 in Roulette is $9.21. b. Based on the expected value from part a, it is not a good idea to play Roulette over and over again. The reason is that the expected value is positive but small. This means that on average, you will win $9.21 for every $10 you bet, but the variance in the game can cause you to lose money in the long run.
For example, if you play 100 rounds of Roulette with a $10 bet on number 12 each time, you would expect to win $921 on average. However, there is a significant chance that you could lose money over these 100 rounds. The more you play, the greater the likelihood of experiencing a losing streak that would offset your winnings.
Therefore, while playing Roulette can be fun and exciting, it is not a sustainable way to make money. The small expected value means that over time, the casino will always come out ahead.
Learn more about sustainable here:
https://brainly.com/question/15377969
#SPJ11
y > -x- 2
y < -5x + 2
Identify a solution to the system
Answers
Move all terms not containing the variable from the center section of the inequality.
