1/3 of the 15 students in the choir have brown hair. How many students in the choir have brown hair?
Answers
To find out how many students in the choir have brown hair we must multiply the number of students by the fraction that represents it, we have a total of 15 students and 1/3 have brown hair, then
\(15\cdot\frac{1}{3}=\frac{15}{3}=5\)Final answer: 5 students have brown hair
Related Questions
How many different sums of money can be made from 4coins of different denomination
Answers
Answer:
15 different sums----------------------
There are various combinations of coins.
1 coin:4 options2 coins:4C2 = 4!/(2!2!) = 6 options3 coins:4C3 = 4!/(3!1!) = 4 options4 coins: 1 optionIn total there are:
4 + 6 + 4 + 1 = 15 different sumsWhich is equivalent to log2^n=4?

Answers
Answer:
D
Step-by-step explanation:
What is the purpose of data? Answer below.
Answers
The purpose of data is to provide information and insights that can be used to make informed decisions, draw conclusions, and gain knowledge about a particular subject or phenomenon.
Data plays a crucial role in various fields, including science, business, research, healthcare, and everyday life.One primary purpose of data is to describe and understand the world around us.
By collecting and analyzing data, we can identify patterns, trends, and relationships that exist within a dataset. This helps us gain a deeper understanding of complex systems and phenomena.
For example, in scientific research, data is used to study the behavior of natural processes, investigate the effects of interventions, and formulate theories and models.
Data also serves as a foundation for making informed decisions. By examining relevant data, individuals and organizations can assess the potential outcomes of different choices and select the most optimal course of action.
Data-driven decision-making enables organizations to improve efficiency, identify opportunities, mitigate risks, and enhance overall performance. In fields like marketing and finance, data is extensively used for market research, customer segmentation, trend analysis, and financial forecasting.
Furthermore, data is crucial for monitoring and evaluating performance. By collecting data over time, organizations can track progress, measure outcomes, and identify areas for improvement. Data-driven monitoring allows for evidence-based assessments and adjustments to strategies or interventions.
Overall, the purpose of data is to provide reliable information that can be used to enhance understanding, support decision-making, and drive progress in various domains. It empowers individuals and organizations with the ability to derive insights, solve problems, and make meaningful contributions to society.
For more such questions on data.
https://brainly.com/question/30459199
#SPJ8
Find the quotient of 10^-4/10^2
Answers
The quotient of 10⁻⁴/10² is 10⁻⁶
How to Find the quotient of 10⁻⁴/10²?Quotient is the result obtained by dividing one quantity by another. It represents the value that is obtained after division.
For example, if you divide 20 by 2, the quotient is 10 because 20 divided by 2 equals 10.
Division law states that:
10ᵃ / 10ᵇ = 10ᵃ⁻ᵇ
In this case have:
10⁻⁴/10² = 10⁻⁴⁻² (Division law)
10⁻⁴/10² = 10⁻⁶
Learn more about quotient on:
brainly.com/question/27862246
#SPJ1
Educators should ensure math instruction is only taught through structured activities rather than through everyday situations and routines.
A- True
B- False
Answers
The statement ' educators should ensure math instruction is only taught through structured activities rather than through everyday situations and routines is True. Option A
Ways to improve mathematics education
They include;
Using hands-on learning methodsUsing visualsIntegration of mathematics gameConnecting math concepts to everyday lifeAllow students to explain their reasoningRewarding students progressThus, the statement ' educators should ensure math instruction is only taught through structured activities rather than through everyday situations and routines is True. Option A
Learn more about early childhood education here:
https://brainly.in/question/7275502
#SPJ1
Answer:
Step-by-step explanation:
false
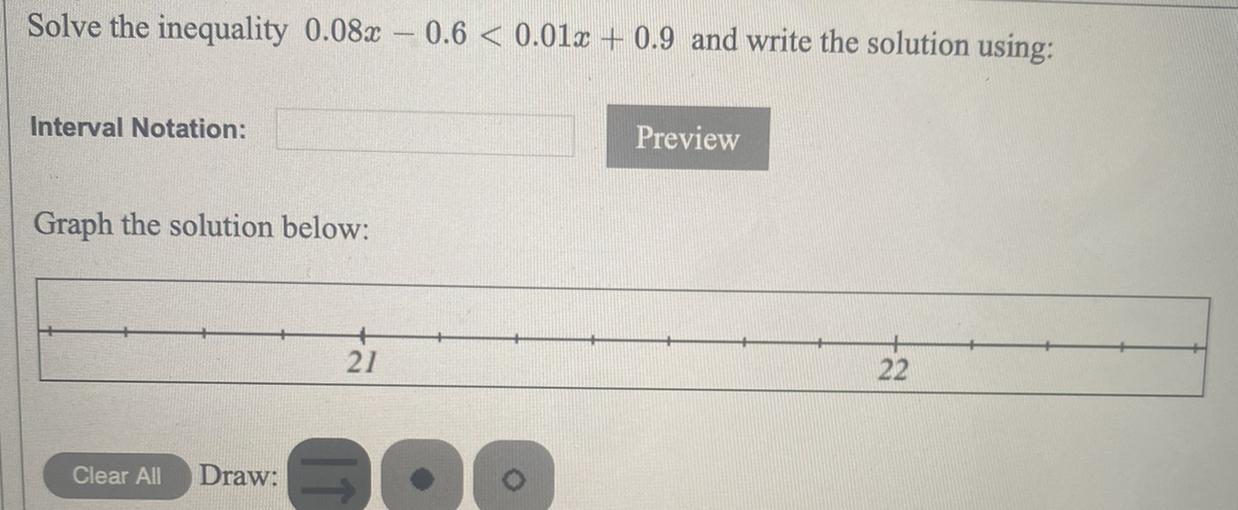
Solve the inequality 0.08x - 0.6 < 0.01x + 0.9 and write the solution using: Interval Notation: Graph the solution below:
Answers
Given
inequality
0.08x - 0.6 < 0.01x + 0.9
Find
Solution of the inequality
Explanation
\(\begin{gathered} 0.08x-0.6<0.01x+0.9 \\ 0.08x-0.01x<0.9+0.6 \\ 0.07x<1.5 \\ x<\frac{1.5}{0.07} \\ \\ x<\frac{150}{7} \\ \end{gathered}\)Interval notation
\(\begin{gathered} (-\infty,\frac{150}{7}) \\ or \\ (-\infty,21.428) \end{gathered}\)Final Answer
Therefore ,the solution in interval notation is
\(\begin{gathered} (-\infty,\frac{150}{7}) \\ or \\ (-\infty,21.428) \end{gathered}\)10. (Bonus points) 55% of the inhabitants of a certain city have green eyes, and 32% have brown hair.
Among those individuals who have green eyes, 15% have brown hair.
(a) What is the probability that a randomly selected person in this city has green eyes and brown
hair?
(b) what is the probability that a randomly selected person in the city has green eyes or brown hair?
(c) what is the probability that a randomly selected person in the city has green eyes given that he or she has brown hair?
Answers
(a) The probability that a randomly selected person in this city has green eyes and brown hair is 0.0825.
(b) what is the probability that a randomly selected person in the city has green eyes or brown hair is 0.0825
(c) The probability that a randomly selected person in the city has green eyes given that he or she has brown hair is 0.2578
What is the probability that a randomly selected person in this city has green eyes and brown hair?(a) To find the probability that a randomly selected person in this city has green eyes and brown hair, we can use the formula:
P(G and B) = P(G) * P(B|G)
Using the given information, we have:
P(G) = 0.55 (55%)
P(B|G) = 0.15 (15% of those with green eyes have brown hair)
Substituting these values, we get:
P(G and B) = 0.55 * 0.15 = 0.0825
(b) To find the probability that a randomly selected person in the city has green eyes or brown hair, we can use the formula:
P(G or B) = P(G) + P(B) - P(G and B)
Using the given information, we have:
P(G) = 0.55 (55%)
P(B) = 0.32 (32%)
P(G and B) = 0.0825
Substituting these values, we get:
P(G or B) = 0.55 + 0.32 - 0.0825 = 0.7875
(c) To find the probability that a randomly selected person in the city has green eyes given that he or she has brown hair, we can use Bayes' theorem, which states that:
P(G|B) = P(B|G) * P(G) / P(B)
Using the given information, we have:
P(B|G) = 0.15 (15% of those with green eyes have brown hair)
P(G) = 0.55 (55%)
P(B) = 0.32 (32%)
Substituting these values, we get:
P(G|B) = 0.15 * 0.55 / 0.32 = 0.2578
Learn more about probability on:
brainly.com/question/251701
#SPJ1
Which of the following statements are true?
Select all that apply.
A. 4 is a perfect cube.
B. 16 is a perfect square.
C. 2,197 is both a perfect square and a perfect cube.
D. 8 is a perfect cube.
E. 18 is neither a perfect square nor a perfect cube.
Answers
The statements that are true are B and D.
Given are some statements we need to check which is true.
Let's analyze each statement:
A. 4 is a perfect cube.
False. 4 is not a perfect cube because there is no integer that can be cubed to give 4.
B. 16 is a perfect square.
True. 16 is a perfect square because it can be expressed as 4^2, where 4 is an integer.
C. 2,197 is both a perfect square and a perfect cube.
False. 2,197 is not a perfect square because there is no integer that can be squared to give 2,197.
However, it is a perfect cube because 13³ equals 2,197.
D. 8 is a perfect cube.
True. 8 is a perfect cube because it can be expressed as 2³, where 2 is an integer.
E. 18 is neither a perfect square nor a perfect cube.
True. 18 is neither a perfect square nor a perfect cube because there is no integer that can be squared or cubed to give 18.
Therefore, the statements that are true are B and D.
Learn more about perfect cube and perfect square click;
https://brainly.com/question/13326108
#SPJ1
can you help me please

Answers
the reason for this is because they could ship goods across the water and make more money off of the goods that way because traveling by boat takes less time then traveling by land
A car is purchased for $21,000. After each year, the resale value decreases by 35%. What will the
resale value be after 3 years?
Answers
Answer:
8859.5
Step-by-step explanation:
if it decreases with 35% then after each year it is worth only 75% of its previous value. so after one year it is worth 75%*21000=15750. the next year it is 75%*15750=11812.2. and after the 3rd year itnis worth 75%*11812.2=8859.5
Given segment AB with A(-2, 5) and B(1, 1), which is the slope of the line parallel to
segment AB?
Answers
Answer:
4/3
Step-by-step explanation:
We find the slope of line AB
Slope = Rise/Run
= 1-5/1+2
= 4/3
We need to use the property that slopes of parallel lines are same. thus the slope of the line parallel to segment AB = 4/3
Find the slope of identity function using points (0,0) and ( 3,3) then from two points (0,0) and (-3,-3). Is there any change in its slope?

Answers
There is no change in its slope as initial and final slope is 1.
What is slope?
In arithmetic, the slope or gradient of a line may be a variety that describes each the direction and therefore the abruptness of the line.
Main body:
formula for slope with two points form is =
y -y₁ =( y₂-y₁ /x₂-x₁ )(x - x₁)
according to question ,
points are (0,0) and (3,3)
y - 0 = (3-0/3-0)(x -0)
y = 3/3 *x
y = x
hence slope of line is 1.
Now points are (0,0) and (-3,-3).
y - 0 = (-3-0/-3-0)(x -0)
y =- 3/-3 *x
y = x
hence slope of line is 1.
So there is no change in its slope.
To know more about slope , visit:
https://brainly.com/question/3493733
#SPJ1
What is the solution to the quadratic inequality?
6x2≥5−13x
[−52,13]
left square bracket negative 5 over 2 comma 1 third right square bracket
(−∞,−13]∪[52,∞)
left parenthesis negative infinity comma negative 1 third right square bracket union left square bracket 5 over 2 comma infinity right parenthesis
[−13,52]
left square bracket negative 1 third comma 5 over 2 right square bracket
(−∞,−52]∪[13,∞)
Answers
The solutions to the quadratic equation are [−5/2,1/3]. Option A
How to determine the solutionGiven the inequality;
6x^2≥5−13x
First, convert to quadratic equation
\(6 {x}^{2} - 5 + 13x \geqslant 0 \)
No, let's solve the quadratic equation using the factorization method
\(6 {x}^{2} + 13x - 5 \geqslant 0\)
Multiply 6 by -5 and find two factor that their product equals the number and their sum equal 13. Those two number are + 15 and -2
Substitute as 15x and 5
-2x in the inequality, we have;
\(6 {x}^{2} +15x - 2x - 5 \geqslant 0\)
Factor the common multipliers
\(3x(2x + 5) - 1(2x + 5) \geqslant 0\)
We have two expressions, written as;
\((3x - 1) (2x + 5)\geqslant 0\)
Let's solve to get the roots of x
\(3x+ 1 \geqslant 0 \)
\(x \geqslant 1/3\)
\(2x + 5 \geqslant 0\)
\(x \geqslant \frac{ - 5}{2} \)
Thus, the solutions to the quadratic equation are [−5/2,1/3]. Option A
Learn more about quadratic equations here:
https://brainly.com/question/1214333
#SPJ1
Solve for y, -2/5 y +2 = -1/5y - 4/3
Answers
Given
\(-\frac{2}{5}y+2=-\frac{1}{5}y-\frac{4}{3}\)The objective is to solve for y, that is, isolate the y-term in one side of the expression.
The first step is to pass "-1/5y" to the left side of the expression by applying the inverse operation
\(\begin{gathered} -\frac{2}{5}y+\frac{1}{5}y+2=-\frac{1}{5}y+\frac{1}{5}y-\frac{4}{3} \\ -\frac{1}{5}y+2=-\frac{4}{3} \end{gathered}\)Next pass "+2" to the right side of the expression
\(\begin{gathered} -\frac{1}{5}y+2-2=-\frac{4}{3}-2 \\ -\frac{1}{5}y=-\frac{10}{3} \end{gathered}\)Finally multiply both sides by -5
\(\begin{gathered} (-\frac{1}{5}y)\cdot(-5)=(-\frac{10}{3})-(-5) \\ y=\frac{50}{3} \end{gathered}\)13,000 inches equals how many miles
Answers
Answer:
0.205177 mi
Step-by-step explanation:
Step 1: Find conversions
12 in = 1 ft
5280 ft = 1 mi
Step 2: Use Dimensional Analysis
\(13000 \hspace{2} in(\frac{1 \hspace{2} ft}{12 \hspace{2} in} )(\frac{1 \hspace{2} mi}{5280 \hspace{2} ft} )\)
0.205177 mi
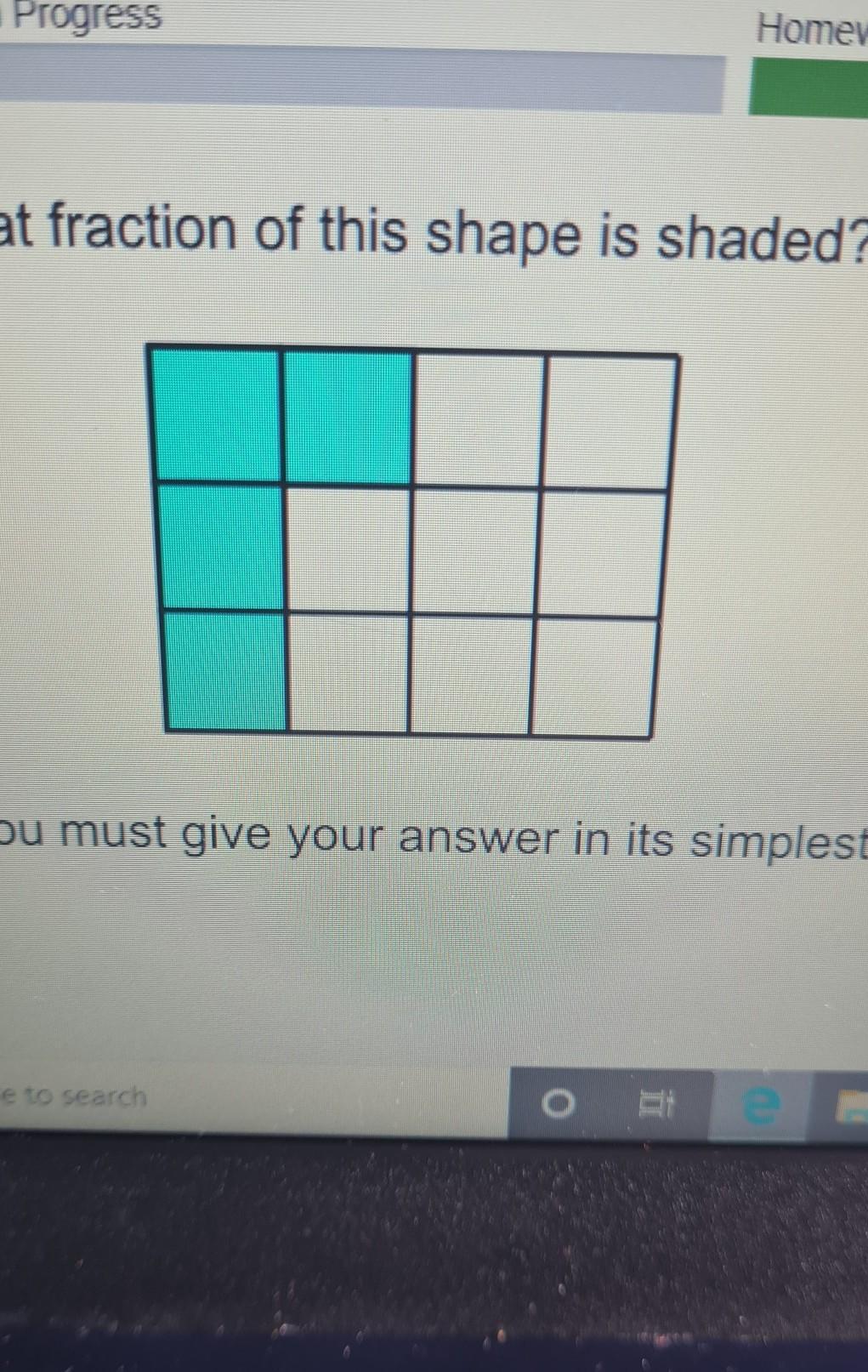
What fraction of this shape is shaded?
You must give your answer in its simplest form.
Type here
Answers
The fraction of the shape which is shaded in simplest form is 1/3.
The square in the diagram provided has a total of 12 boxes .
The number of shaded part is 4
To calculate the shaded fraction of the shape we have to use the formula:
Number of shaded part/ Total number of boxes present.
= 4/12
We can divide the numerator and denominator by 4 to get the simplest form.
= 1/3
The fraction of the shape which is shaded in simplest form is therefore
= 1/3.
Read more about Fraction here https://brainly.com/question/17743912
6.
f-2.3= 18.4
A) f= 16.1
B) f = 20.7
C) f= 19.7
D) f= 17.1
Answers
Answer:
B) f = 20.7 is your answer
what is the measure of angle LKJ? Round to nearest whole degree.
Answers
The angle LKJ in the triangle is 49 degrees.
How to find angles in a triangle?The sum of angles in a triangle is 180 degrees. The measure of the angle LKJ can be found as follows:
Therefore, the angle LKJ can be found using trigonometric ratios as
follows:
Not the triangle is a right angle triangle. Therefore, one of its angles is 90 degrees.
Hence,
tan x = opposite / adjacent
tan x = 8.9 / 7.7
tan x = 1.15584415584
x = tan ⁻¹ 1.15584415584
x = 49.1346675513
Therefore,
angle LKJ = 49 degrees
learn more on angles here: brainly.com/question/29984805
#SPJ1

Create a problem that requires your partner to divide a fraction by a fraction. Then, have your partner solve it. Check the answer by writing a multiplication sentence.
Can anyone help me with this because I don't understand it.
thank you.
Answers
Answer (1/4) * (5/2)
5/2
A tile is selected from seven tiles, each labeled with a different letter from the first seven letters of the alphabet.
The letter selected will be recorded as the outcome.
Consider the following events.
Event X: The letter selected comes before "D".
Event Y : The letter selected is found in the word "CAGE".
Give the outcomes for each of the following events.
If there is more than one element in the set, separate them with commas.

Answers
a) The only outcome that satisfies both events X and Y is the letter C.
b) The outcomes that satisfy either event X or event Y are {A, B, C, E, G}.
c) The complement of event X is {D, E, F, G}.
What is probability?
Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain to happen.
The outcomes for each of the following events are:
(a) Event "X and Y": {C}
To satisfy both events X and Y, the letter selected must come before "D" (which includes the letters A, B, and C) and must be one of the letters in the word "CAGE" (which includes only the letter C). Therefore, the only outcome that satisfies both events X and Y is the letter C.
(b) Event "X or Y": {A, B, C, E, G}
The outcomes that satisfy event X are A, B, and C (since they come before "D"), and the outcomes that satisfy event Y are C, A, G, and E (since they are letters found in the word "CAGE"). Therefore, the outcomes that satisfy either event X or event Y are {A, B, C, E, G}.
(c) The complement of event X: {D, E, F, G}
The complement of event X is the set of outcomes that do not satisfy event X. The outcomes that do not satisfy event X are D, E, F, and G (since they come after or are equal to "D"). Therefore, the complement of event X is {D, E, F, G}.
To learn more about probability from the given link:
https://brainly.com/question/30034780
#SPJ1
There are 10 acts on a talent show. An acrobat comedian dancer guitarist juggler magician pianist singer violinist and a whistler. A talent show host randomly schedules the 10 acts Compute the probability of the events Event A First three acts dancer singer the guitarist in any order Event B the comedian first guitarist second and pianist third
P(A)=
P(B)=
Answers
Answer:
The value of P (A) is 0.00833.
The value of P (B) is 0.00139.
Step-by-step explanation:
It is provided that there are 10 acts on a talent show.
The two events are defined as follows:
A: First three acts dancer, singer and the guitarist in any order
B: The comedian first guitarist second and pianist third
(1)
Compute the number of ways to select 3 acts from the 10 as follows:
\({10\choose 3}=\frac{10!}{3!\cdot (10-3)!}=\frac{10!}{3!\cdot 7!}=120\)
There are 120 ways to select 3 acts from the 10 and only 1 way to select a dancer, singer and the guitarist in any order.
Compute the probability of selecting a dancer, singer and the guitarist in any order as follows:
\(P(A)=\frac{1}{120}=0.00833\)
Thus, the value of P (A) is 0.00833.
(2)
Compute the number of ways to select 3 acts from the 10 (without replacement) and with order as follows:
\(^{10}P_{3}=\frac{10!}{ (10-3)!}=\frac{10!}{ 7!}=720\)
There are 720 ways to select 3 acts from the 10 with order and only 1 way to select the comedian first guitarist second and pianist third.
Compute the probability of selecting the comedian first guitarist second and pianist third as follows:
\(P(B)=\frac{1}{720}=0.00139\)
Thus, the value of P (B) is 0.00139.
What Is 6:3(3+3)= is it 12
Answers
Answer:
Yes it is 12
Step-by-step explanation:
What Is 6:3(3+3)= is it 12
6 : 3 * (3 + 3) =
2 * 6 =
12
I Really Need Help Please

Answers
Answer:
The answer is B
Step-by-step explanation:
A construction crew is pouring concrete to make a floor in a building. The weight of the concrete is proportional to the volume of concrete that has been poured. After pouring 5 cubic feet they know the weight of the concrete is 740 pounds.
(b). The crew wants to create an equation of the form w=k*v to calculate the weight of the concrete based on its volume in cubic feet. What is the value of k in this equation? explain
Answers
The equation that can be used to calculate the concrete weight, w = k·v, and the 740 pounds weight of 5 cubic feet concrete, gives the value of k (which is the density of the concrete) as 148 lb/ft³
What is the density of a substance?The density of a material is the ratio of the mass of the material to its volume.
(b) The weight, w of the concrete is directly proportional to the volume, v of the concrete
The weight of 5 cubic feet = 740 pounds
The equation that can be used to calculate the weight of a given volume of concrete is; w ∝ v
w = k·vWhere;
k = The constant of proportionality
Which gives;
\(k = \dfrac{w}{v}\)
In a proportional relationship between two variables, one variable is a constant multiple of the other such that the ratio of the two variables is a constant, k, which can be found using the value for the data point in the question;
When the weight is 740 pounds, the volume is 5 cubic feet, which gives;
\(k = \dfrac{740\, lb }{5\, ft^3} = 148\, lb/ft^3\)
The value of k in the equation is 148 lb/ft.³Learn more about the constant of proportionality here:
https://brainly.com/question/22167107
#SPJ1
The first three terms of a sequence are given. Round to the nearest thousandth (if necessary).
9,16,23,...
Find the 46th term.
Answers
The 46th term of the sequence is 324.
We have,
To find the 46th term of the sequence, we need to determine the pattern or rule that generates the terms.
Since the difference between consecutive terms is a constant value of 7, we know that this is an arithmetic sequence with a common difference
of 7.
To find the 46th term, we can use the formula for the nth term of an arithmetic sequence:
a(n) = a(1) + (n - 1) d
where a(1) is the first term, d is the common difference, and n is the term number we want to find.
Using the given information, we have:
a(1) = 9
d = 7
n = 46
Plugging these values into the formula, we get:
a (46) = 9 + (46 - 1)7
a (46) = 9 + 45 (7)
a(46) = 9 + 315
a(46) = 324
Therefore,
The 46th term of the sequence is 324.
Learn more about arithmetic sequence here:
https://brainly.com/question/10396151
#SPJ1
find the steps to find the inverse

Answers
The inverse of f(x) = x^(7/9) using exponential notation is f(x) = x^(9/7)
what are inverse functions?An inverse function in mathematics is a function that "undoes" another function.
In other words, if f(x) yields y, then y entered into the inverse of f yields the output x.
An invertible function is one that has an inverse, and the inverse is represented by the symbol f⁻¹.
How to find the inverse functionThe given function is of the form
f(x) = x^(7/9), this is equivalent to ⁹√x⁷
say f(x) = y, then
f(x) = y = x^(7/9)
y = x^(7/9)
solving for the inverse, of y = x^(7/9)
y = x^(7/9)
y^(9/7) = x
interchanging the letters
y = x^(9/7)
hence the inverse function is solved to be f⁻¹(x) = x^(9/7)
Learn more about inverse function :
https://brainly.com/question/11735394
#SPJ1
Mrs. Kreger created the expression
4(h+ 11) - 15 to estimate the number of hours, h, her students need to study each week to earn a certain grade average. According to the expression, how many hours per week does Lindsey need to study if she wants to have an average of at least 90
Answers
Functions are used to show relationship between variables using equations. The number of hours the students need to study to score at least 90 is 15.25 hours
Given
\(f(h) = 4(h + 11) -15\)
To calculate h, when the expression is 90.
We have:
\(4(h + 11) -15 = 90\)
Add 15 to both sides
\(4(h + 11) = 90 + 15\)
\(4(h + 11) = 105\)
Divide both sides by 4
\(h + 11 = 26.25\)
Subtract 11 from both sides
\(h = 26.25-11\)
\(h = 15.25\)
Hence, the students need to study for at least 15.25 hours to have at least 90 marks.
Read more about equations and functions at:
https://brainly.com/question/22964920
factorise x³-4x²+x+6
Answers
The binomial factors of x³- 4x²+x+6 are (x+2), (x+3), and (x-1).
Using the splitting and grouping the terms:
x³ + 4x² + x - 6
= x³ + 2x² + 2x² + x - 6 [Splitting 4x² = 2x² + 2x²]
= (x³ + 2x²) + (2x² + x - 6)
= x² (x + 2) + (2x² + 4x - 3x - 6)
= x² (x + 2) + [ 2x (x + 2) - 3 (x + 2)]
= x² (x + 2) + (x + 2) (2x - 3)
= (x + 2) ( x² + 2x - 3)
= (x + 2) ( x² + 3x - x - 3)
= (x + 2) [x (x + 3) - 1 (x + 3)]
= (x + 2) (x + 3) (x - 1)
Hence, the binomial factors are (x + 2), (x + 3) and (x - 1)
To learn more about factorise here,
https://brainly.com/question/10718512
https://brainly.com/question/24734894
Please help me I don’t understand how to do it. If you can please use a data table to explain how to do it.

Answers
Answer:
The 70% mixture makes up 0.7 liters of the solution whereas the 60% mixture makes up 2.8 liters of the solution.
Step-by-step explanation:
Let us have x liters of the .7 mixture and y liters of the .6 mixture.
We want total liters to be 3.5 which means we need x+y=3.5 . I don't like the decimal in the equation so I'm going to multiply both sides by 10: 10x+10y=35
We also need the .7x+.6y=.62(3.5) . I hate the decimal business going on in this question so I'm going to multiply by 1000 which gives 700x+600y=62(35) .
So we have the system
700x+600y=62(35)
10x+10y=35
I'm going to setup this up for linear combination/elimination.
Multiply bottom equation by 60.
700x+600y=62(35)
600x+600y=60(35)
Subtract equations (bottom from top):
(700-600)x+(600-600)y=35(62-60)
Simplify:
100x+0y=35(2)
100x=70
Divide both sides by 100:
x=70/100
x=7/10
Going back to x+y=3.5 along with x=7/10 or .7 liters to find y.
y=3.5-x with x=.7
y=3.5-0.7
y=2.8
The 70% mixture makes up 0.7 liters of the solution whereas the 60% mixture makes up 2.8 liters of the solution.
Pic added.
Another way to do problem:
.7x+.6(3.5-x)=.62(3.5)
Multiply and distribute:
.7x+2.1-.6x=2.17
Combine like terms on left:
.1x+2.1=2.17
Subtract 2.1 on both sides:
.1x=.07
Multiply both sides by 10:
x=0.7 liters
Now the other acid solution is 3.5-0.7 which is 2.8 litera.

Mrs. Smith has 40 students in her class. The ratio of students who stay after school for extra help to students who stay after school for soccer practice is 3:5. How many students stay after school for soccer practice?
Answers
Answer:
25
Step-by-step explanation:
1: Add up the ratio then divide by the number of students.
3+5=8
40/8=5
2: Each count is equal to 5 students.
3: Multiply the ratio of students who stay after soccer practice by Each count
5*5=25