1/2 divided by 4 in fraction

Answer:

\(P(C\ or\ D) = 1\)

Step-by-step explanation:

Given

\(P(C) = \frac{3}{7}\)

\(P(D) = \frac{4}{7}\)

Required

\(P(C\ or\ D)\)

Since the events are mutually exclusive, then:

\(P(C\ or\ D) = P(C) + P(D)\)

So, we have:

\(P(C\ or\ D) = \frac{3}{7} + \frac{4}{7}\)

Take LCM

\(P(C\ or\ D) = \frac{3+4}{7}\)

\(P(C\ or\ D) = \frac{7}{7}\)

\(P(C\ or\ D) = 1\)

The speed of the boat in still water (x) is 12 mph, and the speed of the current (y) is 9 mph.

To find the speed of the boat in still water and the speed of the current, let's follow these steps:

Step 1: Let x represent the speed of the boat in still water, and y represent the speed of the current. The speed downstream is (x + y) and the speed upstream is (x - y).

Step 2: Use the formula distance = time × speed to write two equations based on the given information.

Downstream: 9(x + y) = 189

Upstream: 63(x - y) = 189

Step 3: Simplify both equations:

Downstream: x + y = 21 (divide both sides by 9)

Upstream: x - y = 3 (divide both sides by 63)

Step 4: Solve the system of equations by adding the two simplified equations:

2x = 24

x = 12

Step 5: Plug the value of x back into either equation to solve for y:

12 + y = 21

y = 9

So, the speed of the boat in still water (x) is 12 mph, and the speed of the current (y) is 9 mph.

Learn more about distance here,

https://brainly.com/question/26046491

#SPJ1

Given the equation:

Let's solve the equation for y.

Take the following steps:

Step 1.

Cross multiply:

Step 2.

Divide both sides by 3:

ANSWER:

y = 14

Answer:

Harry made 9 resolutions.

Step-by-step explanation:

Tim made x resolutions.

Harry made five more, x + 5.

Harry and Tim's together was 13.

x + x + 5 = 13

combine like terms.

2x + 5 = 13

subtract 5

2x = 8

divide by 2

x = 4

Tim made 4 resolutions.

Harry made 4 + 5, that is, 9 resolutions.

Check:

Harry and Tim together is 13.

4 + 9 = 13

Harry made 9 resolutions.

Answer: D. 30.48 miles

Step-by-step explanation:

You basically use Pythagorean Theorem!

a2 + b2 = c2

Square root 20^2 +23^2

=√20^2 + 23^2

=20 x 2 + 23 x 2

= 929

And round it=

30.48 miles.

The total number of tests that Sam and Ben can grade in 3 hours, at their rates, is  90 tests

The number of minutes in 3 hours is:

= 3 x 60 minutes per hour

= 3 x 60

= 180 minutes

The number of tests that Sam can grade in these 3 hours is therefore:

= ( Number of total minutes / Minutes taken by Sam for 6 tests) x 6 tests

= ( 180 / 24) x 6

= 45 tests

The number of tests that Ben can grade are:

= ( 180 / 20 ) x 5

= 45 tests

The total number of tests they can grade in 3 hours is:

= 45 + 45

= 90 tests

Find out more on tests at https://brainly.com/question/17209602

#SPJ1

The equation does not hold true, the ordered pair (3, 10) is not a solution of the equation y = 2x + 6.In this way, we can determine whether an ordered pair is a solution of the given equation or not.

Given the equation y = 2x + 6To determine if an ordered pair is a solution of this equation or not, substitute the values of x and y in the equation. If the equation holds true, then the ordered pair is a solution.

If it is not true, then the ordered pair is not a solution.For example, let's consider the ordered pair (1, 8).

Here, x = 1 and y = 8.Substituting these values in the given equation,

we get: y = 2x + 6 => 8 = 2(1) + 6 => 8 = 8 Since the equation holds true,

the ordered pair (1, 8) is a solution of the equation y = 2x + 6.

Now, let's consider another ordered pair, say (3, 10). Here, x = 3 and y = 10.Substituting these values in the given equation, we get: y = 2x + 6 => 10 = 2(3) + 6 => 10 = 12

To learn more about : equation

https://brainly.com/question/17145398

#SPJ8

7. Radius of circle P = 2       Radius of circle Q = 1

Coordinates of the point of tangency (4,2)

The equation of the tangency line is x = 4

8. AB is not a tangent. BC² ≠ AB² + AC²

9. The three radii of the circle are; CB, CF and CD

A diameter of the circle is BD

A tangent of the circle is GE

A chord of the circle is BD

A secant of the circle is AD

A point of tangency is F

7. To find the radius, identify the diameter of the circle. For the diagram, it can be said that the diameter of the circle P is 4.

The radius then is 4/2 = 2.

The radius of circle q is 2/2 = 1

You could also use the formula

Distance = sqrt((x2 - x1)² + (y2 - y1)²)

8. √4² + √12² = √160

√13 = 169

Therefore AB is not tangent. It is less than BC

9. The line that cuts the circle into two halves is the diameter. The lines than further cuts the diameter into equal parts are the radii's

Find more exercises on finding diameter and radius;

https://brainly.com/question/23891151

#SPJ1

The length of AB is AB = 8 units.

What is distance between two points?

The length of a straight line in the coordinate plane that connects two points in space is what is referred to as their distance. We use the absolute value to calculate the distance between any two points because it is impossible for this distance to be negative.

Consider, the given points A (-4, -3), B (4, -3), C (4, -7), D (-4, -7).

We have to find the length of AB.

Consider, the distance formula,

\(d = \sqrt{(x_2-x_1)^2 +(y_2-y_1)^2}\)

where,

\((x_1, y_1)\) and \((x_2, y_2)\) are the points.

Here,

\((x_1, x_2) = (-4, -3)\\(x_2, y_2) = (4, -3)\)

Plug these values in the above formula,

\(d = \sqrt{(4-(-4))^2+(-3-(-3))^2} \\d = \sqrt{8^2 +0^2} \\d = \sqrt{8^2} \\d = 8\)

Hence, the length of AB is AB = 8 units.

To know more about distance between two points, click on the link

https://brainly.com/question/23848540

#SPJ1

Answer:

x> -20

x= -19,-18,-17,-16,.....

Step-by-step explanation:

-2x + 5 < -x + 25

-2x + x < 25- 5

-x < 20

x> -20

x= -19,-18,-17,-16,......

0.475

1000 milliliters is equal to 1 liter

Answer: 0.475 Liters

Step-by-step explanation: So, we know one liter is exactly 1,000 milliliters...therefore this would have to be a decimal.

Therefore, 475 milliliters to liters would be 0.475 liters.

We can solve this problem by using the law of cosines to find the angle θ between the van's position and Evanston. Let A be the initial position of the van, B be the current position of the van, and C be Evanston. Then we have:

cos(θ) = (AB² + BC² - AC²) / (2AB * BC)

At the start, the van is 5 km east and 0 km north of Evanston, so AB = 5 km. After traveling 9 km due north, the van is at a point 5 km east and 9 km north of Evanston, so BC = 9 km. The distance AC is the hypotenuse of a right triangle with legs 5 km and 9 km, so we have:

AC² = 5² + 9² = 106

Substituting these values into the formula for cos(θ), we get:

cos(θ) = (5² + 9² - 106) / (2 * 5 * 9) = -17/45

To find how fast θ is changing, we need to take the derivative of both sides of the equation cos(θ) = -17/45 with respect to time:

-d(sin(θ)) / dt = d(cos(θ)) / dt

The left side is the rate of change of the y-coordinate of the van's position, which is the same as the van's speed in the northward direction. We know this is 70 km/h. To find the right side, we take the derivative of cos(θ) with respect to time using the chain rule:

d(cos(θ)) / dt = dθ/dt * (-sin(θ))

We want to find dθ/dt, so we can solve for it:

dθ/dt = -d(cos(θ)) / dt / sin(θ) = 70 / (-sin(θ)) = -45 / √146

Therefore, the rate of change of the angle θ is approximately -0.370 radians per hour

Answer:

7.2

Step-by-step explanation:

The 1 looks at the number to the right of it. If the number to the right is 5 or more, the 1 moves up to a 2. Hope this  helps!

Answer:

The answer is 23 I just took this test and got it right

Step-by-step explanation:

Answer: 23

Step-by-step explanation:

There is no change in its slope as initial and final slope is 1.

What is slope?

In arithmetic, the slope or gradient of a line may be a variety that describes each the direction and therefore the abruptness of the line.

Main body:

formula for slope with two points form is =

y -y₁ =( y₂-y₁ /x₂-x₁ )(x - x₁)

according to question ,

points are (0,0) and (3,3)

y - 0 = (3-0/3-0)(x -0)

y = 3/3 *x

y = x

hence slope of line is 1.

Now points are (0,0) and (-3,-3).

y - 0 = (-3-0/-3-0)(x -0)

y =- 3/-3 *x

y = x

hence slope of line is 1.

So there is no change in its slope.

To know more about slope , visit:

https://brainly.com/question/3493733

#SPJ1

Answer: 803.84cm3

Step-by-step explanation:
The formula for finding the volume of a cylinder is πr2h.
In other words, the area of the top face's circle times the height.

To find the circle's area, we first find the radius of the circle. Since the diameter is 8cm, we divide by 2 to get the radius, which is 4cm.

4cm squared is 4cm x 4cm, which is 16cm. 16cm times 3.14 is 50.24cm squared.

Now, we have the area of the circle. 50.24cm squared!

The height is 16cm, so to find the cylinder, we times the area of the circle by the height of the cylinder! So,

16cm x 50.24cm squared = 803.84cm cubed.

The volume of the can of soup is 803.84cm cubed.

According to the angles between intersecting secant and tangent, the value of

angle DF is 52 degrees

angle PQR = 49 degrees

The value of angle DF is solved using the angles of intersecting secant out side the circle

The theorem give the formula in the form

44 = 1/2 (140 - DF)

88 = 140 - DF

DF = 140 - 88

DF = 52 degrees

Using intersection of tangents, for the second figure

exterior angle = 1/2 (major arc - minor arc)

major arc = 360 - 131 = 229

PQR = 1/2 (229 - 131)

PQR = 49 degrees

Learn more about intersecting secant theorem at

https://brainly.com/question/30242636

#SPJ1

Here, we just need to add x and y and subtract it from 180.

x + y = 91 + 42 = 133.

180 - 133 = 47.

Hence, z = 47 degrees.

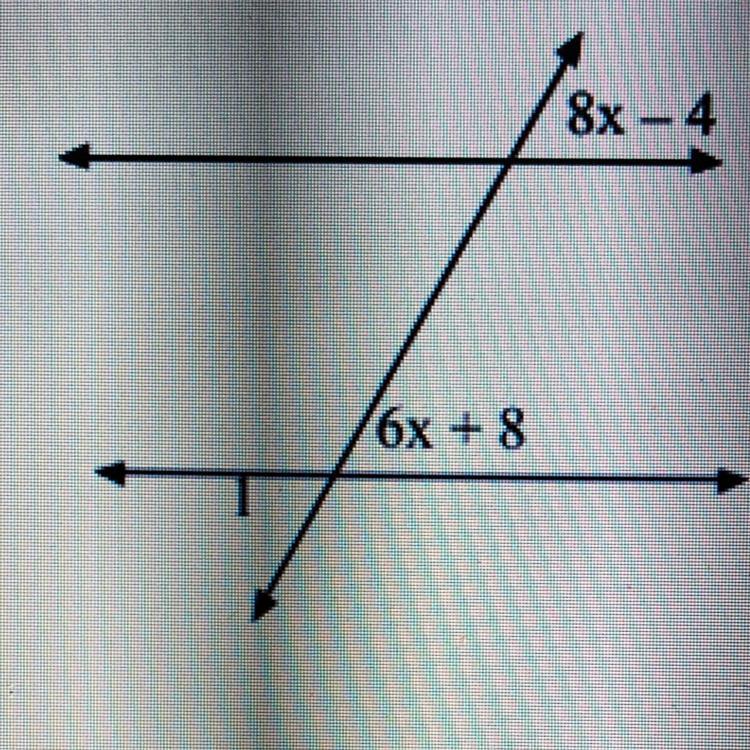
Answer:

Step-by-step explanation:

straight line = 180° we remove the angles x and y and find z

180 - 91 - 42 =

47°

45 and 53 are the correct answers on edge.

Answer:

45 and 53, i got it right on edge

Answer:

a

normal approximation not appropriate in this instance because  

    \(np = 3300 * 0.9998 = 3299.3 > 5\)

and  

     \(nq = 3300 * 0.0002 = 0.66 < 5\)

b

  The probability is  \(P(X = 3300) = 0.52\)

c

 The probability is  \(P(X = 3287) = 0\)

Step-by-step explanation:

From the question we are told that

   The  sample size is  \(n = 3300\)

    The  chance of liking blueberry pie is  \(p = 0.9998\)

    The  chance of not  liking blueberry pie is \(q = 0.0002\)

For normal approximation is possible if  

       \(np > 5\) , \(nq > 5\)

Now let test

      \(np = 3300 * 0.9998 = 3299.3 > 5\)

and  

     \(nq = 3300 * 0.0002 = 0.66 < 5\)  

The  probability that all 3300 people will say they like blueberry pie is mathematically represented as

       \(P(X = 3300) = p^{3300}\)

       \(P(X = 3300) = (0.9998)^{3300}\)

        \(P(X = 3300) = 0.52\)

The probability that 3297 of the people will say that they like blueberry pie is  mathematically represented as

         \(P(X = 3287) = \frac{(np)^{3297! } * e^{-np}}{3297}\)

          \(P(X = 3287) = \frac{0}{\infty}\)

          \(P(X = 3287) = 0\)

Answer:

x > -5, so the correct answer is C.

Answer:

c) 44°

Step-by-step explanation:

the angles labeled '8x-4' and '6x+8' are equal because they are corresponding; we can solve for 'x' by setting them equal to each other

8x - 4 = 6x + 8

2x - 4 = 8

2x = 12

x = 6

substitute 6 for 'x' in '6x+8'

6(6) + 8 = 36 + 8 =  44°

The third term in the expansion of the expression (5x - 7y)³ is 735xy².

Given expression is,

(5x - 7y)³

We have to expand this.

We know that,

(a + b)³ = a³ - 3a²b + 3ab² - b³

Using this,

(5x - 7y)³ = (5x)³ - (3 × (5x)² × 7y) + (3 ×(5x) × (7y)²) - (7y)³

               = 125x³ - (3 × 25x² × 7y) + (3 × 5x × 49y²) - 343y³

               = 125x³ - 525x²y + 735xy² - 343y³

Here the third term is 735xy².

Hence the third term is 735xy².

Learn more about expansion of expressions here :

https://brainly.com/question/28400521

#SPJ1

Answer:

12 liters

Step-by-step explanation:

Let the capacity sum of the 5 containers be X

13 = X / 5

X = 65 liters

Average capacity of the six = ( 65 + 7 )/ 6 liters

= 72/6 liters

= 12 liters

You end up at the point (5, 5).

Answer:

I think so Brand B should be bought because more ounces of rice in just a little bit expensive than brand A and more ounces of rice would work in just 3.19 dollars.

Answer:

15.0

Step-by-step explanation:

we are finidng the adjacent angle, they have given us the opposite and the missing adjacent side so we use tan

tan25=7/x

since x is at the bottom then switch

x= 7/tan25

x= 15. 012

Answer:

x = 15.01

Step-by-step explanation:

Given degrees 25

Since x is between the right angle and 25, x is adjacent

7 being the other shortest side would be the opposite

Given adjacent and opposite, you can use tangent

Tangent = opposite/adjacent

Tan(25) = 7/x

0.4663076582 = 7/x

x = 7/0.4663076582 (use calculator)

Solution: x = 15.0115484421

The input-output tables represent a function that will be table C and table D.

A function is an assertion, concept, or principle that establishes an association between two variables. Functions may be found throughout mathematics and are essential for the development of significant links.

If the value of the output is single for each distinct value of the input. Then the table represents the function.

In option A, the number of outputs is 2 for a single value of the input that is x = 1. So, it does not represent a function.

In option B, the number of outputs is 2 for a single value of the input that is x = 5. So, it does not represent a function.

In option E, the number of outputs is 2 for a single value of the input that is x = 1. So, it does not represent a function.

The input-output tables represent a function that will be table C and table D.

More about the function link is given below.

https://brainly.com/question/5245372

#SPJ5