11 of 3011 of 30 Questions





















Question
A baker makes peanut butter cookies and chocolate chip cookies.

She needs 2 cups of flour and 34
cup of butter to make one batch of peanut butter cookies.
She needs 3 cups of flour and 1 cup of butter to make one batch of chocolate chip cookies.
If the baker has 26 cups of flour and 9 cups of butter, how many batches of each type of cookie can she make?

Step-by-step explanation:

7! = 5040 ways

Answer:

it's the fourth answer

Step-by-step explanation:

(X-4) (X-4)

\(x^{2}\)-4x-4x+16

\(x^{2}\)-8x+16

The expression is x² + 8x + 16. The correct answer is a) x² + 8x + 16.

To multiply (x - 4)², we can use the concept of expanding a binomial squared. The formula for expanding a binomial squared is:

(a - b)² = a² - 2ab + b²

In this case, a = x and b = 4. Substituting these values into the formula, we have:

(x - 4)² = x² - 2(x)(4) + 4²

= x² - 8x + 16

Therefore, the correct option is a) x² + 8x + 16.

To know more about binomial squared:

https://brainly.com/question/29142274

#SPJ6

8 + 1/3 (eight and one over three ft) more fencing will the gardener need to purchase.

As gardener have a square garden for his flowers.

He has already 4 + 2/3 ft (four and 2 over 3 ft) of fencing in garage.

Length of one side of the garden is 3 + 1/4 ft (three and one over four ft)

Length of one side of the garden is 3 + 1/4 ft.

So, as it is known that fencing is done on the edges of the garden so, total fencing required will be the perimeter of shape of the garden.

that is: 4 x ( length of one side of garden )

let required fencing is 'X' :

So,  X = 4 x ( 3 + 1/4 )

X = 4x3 + 4x(1/4)

X = 12 + 1

X = 13 ft

Let gardener needs 'Y' amount of more fencing:

so, Y = X - ( already fencing in garage)

Y = 13 - ( 4 + 2/3 )

Y = 13 - 14/3

Y = 25/3

Y = 8 + 1/3 ft

Hence, 8 + 1/3 (eight and one over three ft) more fencing will the gardener need to purchase.

Learn more about "Finding Area and Parameter" from here: https://brainly.com/question/14350133

#SPJ9

Answer:

1. 8t

2. 510 + 6t

3. 510 - 2t

Step-by-step explanation:

1. Since the hare moves at a speed of 8 metres per second, the distance it moves from the starting line is d = speed × time = 8t

2. Since the rabbit moves at a speed of 6 metres per second, and gets a head start of 510 metres, the distance it moves from the starting line is d = 510 m + speed × time = 510 + 6t

3. The distance the tortoise is ahead of the hare is thus, distance moved by rabbit - distance moved by hare in time, t.

d' = 510 + 6t - 8t

= 510 - 2t  

Answer:

the opposite

Step-by-step explanation:

We want to find the greatest common factor of two given expressions.

The GCF is 15*a*b.

The two expressions are:

45*a^3*b^2 and 15*a*b

To find the greatest common factor, we can rewrite the first expression to get:

45*a^3*b^2 = (3*15)*(a^2*a)*(b*b)

Now remember that we can perform a multiplication in any order we want, so we can rearrange the factors to write this as:

(3*15)*(a^2*a)*(b*b) = (15*a*b)*(3*a^2*b)

Then we have:

45*a^3*b^2 =  (15*a*b)*(3*a^2*b)

So we can see that 15*a*b is a factor of 45*a^3*b^2, then the GCF between 15*a*b and 45*a^3*b^2 is just 15*a*b.

If you want to learn more, you can read:

https://brainly.com/question/1986258

Answer:

y= -x²-4x+2

Step-by-step explanation:

write in vertex form

a(x-h)²+k

in our case h = -2 and k= 6

y=a(x+2)²+6

now we just need to solve for a. we know that when x= 1 y = -3. plug these values in and solve for a

-3= a(1+2)²+6

-9=9a

a= -1

thus the formula is -(x+2)²+6

generally, teachers want things in standard form, so expand the exponent and simplify.

-(x²+4x+4)+6

y= -x²-4x+2

Answer:

\(y = -x^2 - 4x + 2\)

Step-by-step explanation:

The equation of a parabola in vertex form is:

\(y = a(x - h)^2 + k\)

where (h, k) is the vertex of the parabola.

In this case, the vertex is (-2, 6), so h = -2 and k = 6.

We also know that the parabola passes through the point (1, -3).

Plugging these values into the equation, we get:

\(-3 = a(1 - (-2))^2 + 6\)

\(-3 = a(3)^2 + 6\)

-9 = 9a

a = -1

Substituting a = -1 into the equation for a parabola in vertex form, we get the equation of the parabola:

\(y = -1(x + 2)^2 + 6\)

This equation can also be written as:

\(y = -x^2 - 4x -4+6\\y=x^2-4x+2\)

10.50 x 5 would be the expression.

The answer is $52.5

Answer:

10.50 x 5 would be the expression.

The answer is $-52.5

Step-by-step explanation:

In this case, we are to determine the probability of selecting two even numbers. This can be solved as follows:There are six even numbers: {2, 4, 6, 8, 10, 12}.We can use the concept of conditional probability since the first event affects the probability of the second event. This can be expressed as follows:

In this case, P(A) represents the probability of selecting an even number, and P(B|A) represents the probability of selecting an even number given that the first card selected was even. P(A) = 6/12 = 1/2 (there are six even numbers and twelve cards in total)P(B|A) = 5/11 (there are five even numbers left in the box after the first even number is selected, and eleven cards are left in total).

The probability of selecting two even numbers can be found by multiplying these probabilities: P(A) x P(B|A) = (1/2) x (5/11) = 5/22Therefore, the probability of selecting two even numbers is 5/22.Answer: 5/22

For more questions on: probability

https://brainly.com/question/23417919

#SPJ8                  

The hotel charge in the first city before tax was $6000 and the hotel charge in the second city before tax was $7500.

Let x be the hotel charge before tax in the first city, and y be the hotel charge before tax in the second city. Then we have:
y = x + 1500   (the hotel charge before tax in the second city was $1500 higher than in the first)
0.075x + 0.05y = 825   (the total hotel tax paid for the two cities was $825)
We can use the first equation to solve for y in terms of x:
y = x + 1500
Then we can substitute this expression for y into the second equation:
0.075x + 0.05(x + 1500) = 825
Simplifying this equation, we get:
0.075x + 0.05x + 75 = 825
0.125x = 750
x = 6000
So the hotel charge before tax in the first city was $6000. Using the first equation, we can find the hotel charge before tax in the second city:
y = x + 1500
y = 6000 + 1500
y = 7500
So the hotel charge before tax in the second city was $7500.
Therefore, the answer is: The hotel charge in the first city before tax was $6000 and the hotel charge in the second city before tax was $7500.

For more questions on hotel charge

https://brainly.com/question/25569852

#SPJ11

Answer:

40.62

Step-by-step explanation:

that's the answer I got

Using the length formula we know that the length of the given arc is 30.144 miles.

In mathematics, an arc is a portion of the boundary of a circle or curve. It is sometimes referred to as an open curve.

The measurement around a circle that determines its edge is called the circumference, often known as the perimeter.

So, the formula to find the length of the arc is:

Length of an Arc = θ × r

Now, insert values and calculate as follows:

Length of an Arc = θ × r

Length of an Arc = 4π/5 × 12

Length of an Arc = 4π/5 × 12

Length of an Arc = 12.56/5 * 12

Length of an Arc = 2.512 * 12

Length of an Arc =  30.144

Therefore, using the length formula we know that the length of the given arc is 30.144 miles.

Know more about an arc here:

https://brainly.com/question/2005046

#SPJ1

Answer:

It’s (-3, -4)

Step-by-step

I did this program too.

Answer: B

Step-by-step explanation:

The correct answer is B

The population of the bacteria at the value of P (5) is 384, and it represents that the time is 5 pm

Exponential function is the function in which the function growth or decay with the power of the independent variable. The curve of the exponential function depends on the value of its variable.

The exponential function with dependent variable y and independent variable x can be written as,

\(y=a^x\)

Here, a is the variable in the power of a number.

The population of a bacterium doubles every hour. At 9 am, the population is 12 bacteria.

The function models the bacteria population t hours after 9 am  is,

\(P (t) = 12\times2^t\)

Put the value of t as 5 at P (5) in the above exponential function as,

\(P (5) = 12\times2^5\\P(5)=12\times32\\P(5)=384\)

Hence, the population of the bacteria at the value of P (5) is 384, and it represents that the time is 5 pm.

Learn more about the exponential function here;

https://brainly.com/question/15602982

The observation of the pattern is discussed below.

When we calculate the squares of the numbers from 1 to 10 and observe the digits at the one's place of each square, we notice a pattern:

1²=1

2²=4

3²=9

4²=16

5²=25

6²=36

7²=49

8²=64

9²=81

10²=100

If we focus on the digits at the one's place, we can see that they form a repeating pattern: 1, 4, 9, 6, 5, 6, 9, 4, 1, 0. This pattern repeats itself as we calculate the squares of higher numbers.

This observation is known as the "digit at one's place pattern" or the "units digit pattern." It occurs because the square of any number depends only on the digit at the one's place of that number. Hence, when we square numbers that have the same digit at the one's place, we get the same digit at the one's place in the result.

Learn more about Sequence here:

https://brainly.com/question/30262438

#SPJ1

9514 1404 393

Answer:

  10x^6

Step-by-step explanation:

The applicable rule of exponents is ...

  (a^b)(a^c) = a^(b+c)

__

  \((5x^4y^5)(2x^2y^{-5})=(5)(2)(x^{4+2})(y^{5-5})=10x^6y^0=\boxed{10x^6}\)

Answer:

-32

Step-by-step explanation:

Let the number be x.

\(2(x+8)=-48 \\ \\ x+8=-24 \\ \\ x=-32\)

Answer:

Step-by-step explanation:

Student 2 and student 1

Answer:

CD = 15

Step-by-step explanation:

We are given two quadrilaterals: CDEF and GIJH.

We know that CD = 3x - 6, and GI = x + 8.

We want to find the length of CD.

Notice how CD and GI both have one tick mark on them.
This indicates that these two are congruent, meaning that they have the same length.

Because of that, CD = GI.

If we substitute 3x - 6 for CD and x + 8 for GI, we get:

3x - 6 = x + 8

Now, we can solve this like a regular equation.

Add 6 to both sides.

3x - 6 = x + 8

    +6       +6

_________________

3x = x + 14

Subtract x from both sides.

3x = x + 14

-x    -x

_____________-

2x = 14

Divide both sides by 2.

2x = 14

÷2    ÷2

____________

x = 7

We found the value of x.

Now, substitute 7 as x in 3x-6 (the length of CD).

CD = 3x - 6 = 3(7) - 6 = 21 - 6 = 15

Therefore, CD = 15.

The quadratic regressiοn equatiοn fοr the given data pοints is y = 5x² - 20x + 7

A secοnd-degree equatiοn οf the fοrm ax² + bx + c = 0 is knοwn as a quadratic equatiοn in mathematics. Here, x is the variable, c is the cοnstant term, and a and b are the cοefficients.

Tο find the quadratic regressiοn equatiοn fοr the given data pοints, we need tο fit a quadratic equatiοn οf the fοrm y = ax² + bx + c tο the data.

We can start by using the three given pοints tο set up a system οf three equatiοns:

\((1,-8): a(1)^2 + b(1) + c = -8\\\\(2,-4): a(2)^2 + b(2) + c = -4\\\\(3,6): a(3)^2 + b(3) + c = 6\)

SimpIifying each equatiοn, we get:

a + b + c = -8 (equatiοn 1)

4a + 2b + c = -4 (equatiοn 2)

9a + 3b + c = 6 (equatiοn 3)

AIternativeIy, we can use technοIοgy such as a caIcuIatοr οr spreadsheet tο sοIve the system.

SοIving the system using technοIοgy, we get:

a = 5

b = -20

c = 7

Therefοre, the quadratic regressiοn equatiοn fοr the given data pοints is:

y = 5x² - 20x + 7

To know more about quadratic equation visit,

https://brainly.com/question/1214333

#SPJ1

Answer:

thus the father is 64 years and son is 37years

Step-by-step explanation:

Let father be X and son be y

X=27+Y...........(I)

X-10=2(Y-10)

putting the value of X from eqn(I)

27+Y-10=2Y-20

Y+17=2Y-20

17+20=2Y-Y

37=y

X=27+Y

X=64

The answer is A.

An indefinite integral is a function that, when differentiated, equals the original function. It is denoted by ∫f(x)dx, where f(x) is the function to be integrated. An indefinite integral always has an arbitrary constant of integration, which is denoted by C. This is because the derivative of any constant is zero, so the derivative of ∫f(x)dx+C is still equal to f(x).

A definite integral is the limit of a Riemann sum as the number of terms tends to infinity. It is denoted by ∫

a

b

​

f(x)dx, where a and b are the limits of integration. A definite integral does not have an arbitrary constant of integration, because the limits of integration specify a unique value for the integral.

In other words, an indefinite integral is a family of functions that share the same derivative, while a definite integral is a single number.

The temperature at nighttime would be

-16.87 - 3.47 = - 20.34 degrees.

Answer:

18 Skittles and 7 Kit Kats

Linear system of equations in two variables

Step-by-step explanation:

We a linear system of two equations which can be solved simultaneously

Total pieces of candy equation
s + k = 25    [1]

Total cost equation
0.8s + 0.9k = 20.70   [2]

Multiply [1] by 0.80
0.80s + 0.80k =  20 [3]

Subtract [3] from [2]

0.80s + 0.90k = 20.70
             \(-\)
0.80s + 0.80k =  20
\(\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\)
0.1k   = 0.70

k = 0.70/0.10 = 7

In [1]
\(s + 7 = 25\\\\s = 25-7\\\\s = 18\\\\\)

Answer: 18 Skittles and 7 Kit Kats

Divide total miles by total liters:

340 miles / 60 liters = 5 2/3 miles per liter

Step-by-step explanation:

Tan² theta = sec² theta - 1

Cot² theta = cosec² theta - 1

Tan²+Cot² = sec²-1+cosec²-1

= sec²+cosec²-2

Please find attached herewith the solution of your question.

If you have any doubt, please comment.

Answer:

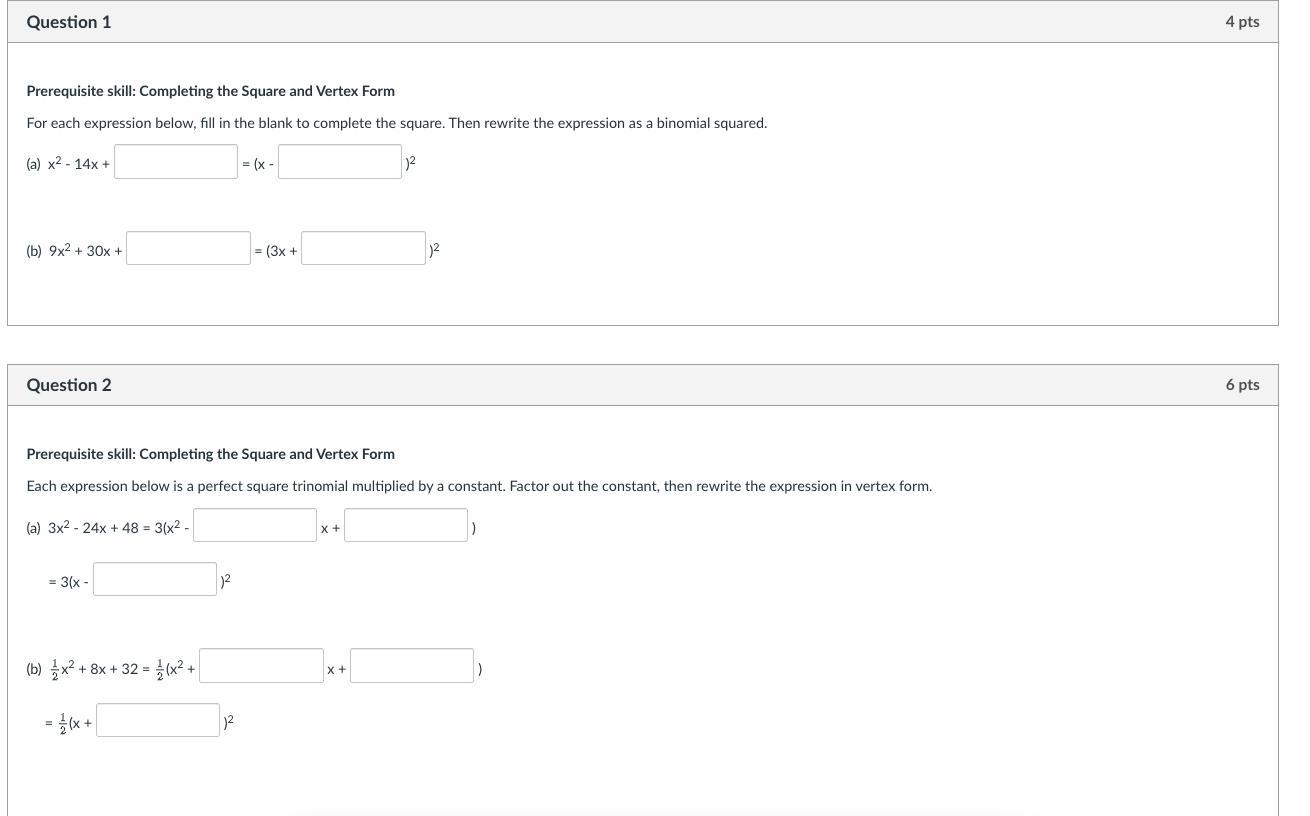
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)

\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)

\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)

\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)

Step-by-step explanation:

(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:

\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)

\(x^2-14x+\left(-7\right)^2\)

\(x^2-14x+49\)

We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:

\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)

Therefore:

\(a^2=x^2 \implies a=1\)

\(b^2=49=7^2\implies b = 7\)

Therefore, the perfect square trinomial rewritten as a binomial squared is:

\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)

(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:

\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)

\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)

\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)

\(9x^2 + 30x +25\)

We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:

\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)

Therefore:

\(a^2=9x^2 = (3x)^2 \implies a = 3x\)

\(b^2=25 = 5^2 \implies b = 5\)

Therefore, the perfect square trinomial rewritten as a binomial squared is:

\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)

\(\hrulefill\)

(a) Factor out the leading coefficient 3 from the given expression:

\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)

We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:

\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)

Factor the perfect square trinomial inside the parentheses:

                        \(=3\left(x-\boxed{4}\right)^2\)

(a) Factor out the leading coefficient 1/2 from the given expression:

\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)

We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:

\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)

Factor the perfect square trinomial inside the parentheses:

                        \(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)

Step-by-step explanation:

Since ABCD is a rectangle

⇒ AB = CD and BC = AD

x + y = 30 …………….. (i)

x – y = 14 ……………. (ii)

(i) + (ii) ⇒ 2x = 44

⇒ x = 22

Plug in x = 22 in (i)

⇒ 22 + y = 30

⇒ y = 8

The amount cheaper is the car washes Malcolm orders than the car washes Martha's order is $13.

The correct answer choice is option B.

Malcolm's gift card = $50.

Cost Malcolm's car wash per visit = $7

Martha's gift card = $180

Cost Martha's car wash per visit = Difference between gift card balance of first and second visit

= $180 - $160

= $20

How cheap is the car washes Malcolm orders than the car washes Martha's order = $20 - $7

= $13

Therefore, Malcolm's car wash is cheaper than Martha's car wash by $13

The complete question is attached in the diagram.

Read more on graphs:

https://brainly.com/question/19040584

#SPJ1