1. What is the Mean Treatments?
2. What is the Mean Square Treatments?
3. What is the Mean Squared Error?
4. What is the F-Test Value? Based on our F-Test Value, should
we reject the Null Hypothesis (
Answers
The terms "Mean Treatments," "Mean Square Treatments," "Mean Squared Error," and "F-Test Value" are commonly used in the analysis of variance (ANOVA) framework.
However, without the specific data or research context, it is not possible to provide accurate values or interpretations for these parameters.
In general, the Mean Treatments refers to the average of the treatment group means in an ANOVA, which represents the effect of the different treatments or factors being studied. The Mean Square Treatments is the sum of squares for treatments divided by its degrees of freedom, which provides an estimate of the treatment effect variability. The Mean Squared Error represents the average of the error or residual variances within each treatment group. The F-Test Value is the ratio of the Mean Square Treatments to the Mean Squared Error and is used to test the null hypothesis of no treatment effects.
To determine whether to reject the null hypothesis based on the F-Test Value, a critical value or p-value needs to be compared. If the calculated F-Test Value exceeds the critical value or the p-value is below a predetermined significance level, typically 0.05, then the null hypothesis is rejected, indicating the presence of significant treatment effects.
However, without specific values or data, it is not possible to provide a definitive answer regarding the rejection of the null hypothesis.
To learn more about Mean Square - brainly.com/question/30404070
#SPJ11
Related Questions
I am attaching a picture of the question as you can see my teacher has already answered it but she wants me to show how she got the answer

Answers
Surface area of a square pyramid:
\(\begin{gathered} SA=B+\frac{1}{2}p\cdot s \\ \\ B=\text{area of the base} \\ p=\text{perimeter of the base} \\ s=\text{slant height} \end{gathered}\)To find the surface area of the given pyramid as you don't have the length of the slant height, use the height of the pyramid and the radius of the base to form a right triangle and find the slant height:
Pythagorean theorem for the right triangle above:
\(\begin{gathered} s^2=h^2+(\frac{1}{2}b)^2 \\ \\ s=\sqrt[]{h^2+(\frac{1}{2}b)^2} \\ \\ s=\sqrt[]{(12in)^2+(\frac{1}{2}\cdot18in)^2} \\ \\ s=\sqrt[]{(12in)^2+(9in)^2} \\ \\ s=\sqrt[]{144in^2+81in^2} \\ \\ s=\sqrt[]{225in^2} \\ \\ s=15in \end{gathered}\)Perimeter of the base is:
\(\begin{gathered} p=4b \\ p=4\cdot18in \\ p=72in \end{gathered}\)Area of the square base:
\(\begin{gathered} B=b^2 \\ B=(18in)^2 \\ B=324in^2 \end{gathered}\)Then, the surface area of the given pyramid is
\(\begin{gathered} SA=324in^2+\frac{1}{2}\cdot72in\cdot15in \\ \\ SA=324in^2+540in^2 \\ SA=864in^2 \end{gathered}\)

Nesmith Corporation's outstanding bonds have a $1,000 par value, a 6% semiannual coupon, 11 years to maturity, and an 8% YTM. What is the bond's price?
Answers
The price of the bond is approximately $721.92.
A bond is a debt security that an investor lends to an entity in exchange for interest payments and the return of the principal at the end of the bond term. The price of a bond can be calculated using the following formula:
Bond price = [C / (1 + r)^n] + [F / (1 + r)^n]
Where:
F = face value of the bond
C = coupon rate
n = number of years remaining until maturity
r = yield to maturity (YTM)
Given data:
Face value (F) = $1,000
Coupon rate (C) = 6% semi-annually
Years to maturity (n) = 11
Yield to maturity (YTM) = 8%
To calculate the bond price, we need to use semi-annual coupons since the coupon is paid twice a year. We adjust the coupon rate, years to maturity, and yield to maturity accordingly.
Coupon rate (C) = 6% / 2 = 3% per half year
n = 11 × 2 = 22
r = 8% / 2 = 4% per half year
Plugging the given values into the formula:
Bond price = [30 / (1 + 0.04)^11] + [1000 / (1 + 0.04)^22]
≈ $721.92
Therefore, The bond costs around $721.92.
Learn more about bonds
https://brainly.com/question/31358643
#SPJ11
is it possible to choose (2n 1)^2 points in the disc of radius n such that the distance between any two of them is greater than 1?
Answers
Answer: its (4f 5) ^3
Step-by-step explanation:
If f(x) = -2x + 3 and g(x) = 4x - 3, which is greater, f(5) or g(-2)?
Answers
Find the midpoint of the hypotenuse.

Answers
Bend be be K’s or if if so
find dy/dx. x = t2, y = 8 − 2t
Answers
The derivative of y with respect to x is -2.
To find \(\frac{dy}{dx}\), we first need to express y and x in terms of a common variable, which we choose to be t.
Given x = t^2, we can differentiate both sides with respect to t using the chain rule to obtain:
\(\frac{dx}{dt}\) = 2t
Solving for t, we get:
t = (1/2) \(\frac{dx}{dt}\)
Substituting this value of t into the equation y = 8 - 2t, we get:
y = 8 - 2((1/2) \(\frac{dx}{dt}\))
Simplifying, we get:
y = 8 -\(\frac{dx}{dt}\)
Differentiating both sides with respect to x using the chain rule, we get:
\(\frac{dy}{dx}\) = d/dx(8 - \(\frac{dx}{dt}\))
Using the chain rule again, we have:
\(\frac{dy}{dx}\) = - \(\frac{d(dx/dx)/dt }\)
Since \(\frac{dx}{dt}\) = 2t, we can substitute this to obtain:
\(\frac{dy}{dx}\) = -\(\frac{d2t}{dt}\)
Taking the derivative of 2t with respect to t, we get:
\(\frac{dy}{dx}\) = -2
Therefore, the derivative of y with respect to x is -2.
To know more about derivative refer here
https://brainly.com/question/30365299#
#SPJ11
A student solved z + (-0.72) = -2.5 for z using the
following steps.
Step 1: Z + (-0.72) + (-0.72) = -2.5+ (-0.72)
z = -2.5+ (-0.72)
Step 2:
Step 3:
z = -3.22
What was the student's error?
Answers
Answer:
Mistake in step1Step-by-step explanation:
Given
z + (-0.72) = -2.5Solving in steps
1. ⇒ z + (-0.72) - (-0.72) = -2.5 - (-0.72)2. ⇒ z = - (2.5 - 0.72)3. ⇒ z = - 1.78The student's mistake was adding (-0.72) instead of - (-0.72) or 0.72
Answer:
To solve, you must use the inverse operation. In step 1, -0.72 should have been subtracted from both sides, not added. Otherwise, 0.72 should have been added to both sides, not -0.72.
Step-by-step explanation:
botanists placed seed baits at 5 sites in region a (1) and 6 sites in region b (2) and observed the number of ant species attracted to each site. the botanists know that the populations are normally distributed, and they calculate the mean and standard deviation for the number of ant species attracted to each site in the samples. is there evidence to conclude that a difference exists between the average number of ant species in the two regions? draw the appropriate conclusion, using
Answers
More information is needed to draw a conclusion on the difference between the average number of ant species.
To draw a conclusion on the difference between the average number of ant species in the two regions, we need additional information. The botanists have collected data on the number of ant species attracted to sites in region A (1) and region B (2).
However, we require the calculated means and standard deviations for each sample to proceed with statistical analysis. With these values, we can perform a hypothesis test, such as an independent samples t-test, to determine if there is evidence to conclude that a difference exists between the average number of ant species in the two regions. Without the means and standard deviations, it is not possible to make a definitive conclusion.
To learn more about “standard deviation” refer to the https://brainly.com/question/5566419
#SPJ11
Based on the given information, the botanists placed seed baits at 5 sites in region A and 6 sites in region B, and observed the number of ant species attracted to each site. They calculated the mean and standard deviation for the number of ant species attracted to each site in the samples. We can determine if there is evidence to conclude that a difference exists between the average number of ant species in the two regions by performing a t-test.
To conduct a t-test, we compare the means of the two samples and take into account the standard deviations. The null hypothesis (H0) states that there is no difference between the average number of ant species in the two regions, while the alternative hypothesis (Ha) states that there is a difference.
The t-test will calculate a t-value, which we can compare to a critical value from the t-distribution table. If the t-value is greater than the critical value, we reject the null hypothesis and conclude that there is evidence of a difference between the average number of ant species in the two regions.
To draw the appropriate conclusion, we need the calculated t-value and the critical value for the desired level of significance (usually 0.05 or 0.01). Without these values, we cannot provide a specific conclusion. However, if the calculated t-value is greater than the critical value, we can conclude that there is evidence of a difference between the average number of ant species in the two regions.
t-test: https://brainly.com/question/6501190
#SPJ11
Triangle QRS has vertices Q(−2, 2), R(−3, −4), and S(1, −2)
Write the coordinate notation for a translation of 7 units right and 4 units down.
Answers
The coordinate notation for a translation of 7 units right and 4 units are:
Q: (5,-2)
R: (4,-8)
A: (8,-6)
What is the Triangle?To perform a translation of 7 units right and 4 units down on Triangle QRS, we add 7 to the x-coordinates and subtract 4 from the y-coordinates of each vertex. The coordinate notation for the translated triangle, denoted as Q'R'S', is:
Q': (−2 + 7, 2 - 4) = (5, -2)
R': (−3 + 7, −4 - 4) = (4, -8)
S': (1 + 7, −2 - 4) = (8, -6)
So, the coordinate notation for the translated triangle Q'R'S' is Q'(5, -2), R'(4, -8), and S'(8, -6).
Learn more about Triangle from
https://brainly.com/question/15525396
#SPJ1
an arrangement of letters such that the uniform substitution of words or phrases in the place of letters results in an argument is called an
Answers
An arrangement of letters such that the uniform substitution of words or phrases in the place of letters results in an argument is called a cryptogram, An arrangement of letters such that the uniform substitution of words or phrases in the place of letters results in an argument is called a "propositional form" or "logical form."
What is the difference between phrase and word? Word is a synonym of a phrase. Word is a conjunction of a phrase. is that phrase to express (an action, thought, or idea) by means of words while word is to ply or overpower with words?
Students often make the mistake of using synonyms of “and” each time they want to add further information in support of a point they’re making or to build an argument. Here are some cleverer ways of doing this.
To know more about propositional form:- https://brainly.com/question/30245940
#SPJ11
Answer this question and show me how to check it

Answers
In order to rewrite these values in the standard form, let's calculate the product with the power of 10 from each number.
For the length, we have:
\(\begin{gathered} 8\cdot10^4 \\ =8\cdot10000 \\ =80000\text{ meters} \end{gathered}\)For the thickness, we have:
\(\begin{gathered} 5\cdot10^{-6} \\ =5\cdot0.000001 \\ =0.000005\text{ meters} \end{gathered}\)Evaluate the function.
f(x)=-x^2-14
Find f(9)
Answers
Identify the factor and levels in the following scenario: The Hyppo (a gourmet ice pop store) is trying to test out new dip flavors in which customers can dip their popsicles (strawberry, orange, and banana). All of the popsicles are made the same, utilizing the same simple chocolate flavoring for experimental purposes, but the dips are randomly applied. Twenty regular customers are given the popsicles with the dips on them in a random order, and are asked to rate them from 1-3.
Group of answer choices
Factor = dip flavor. Levels = ratings 1-3
Factor = strawberry, orange, and banana. Levels = dip flavor
Factor = the hyppo location. Levels = 20 regular customers
Factor = dip flavor. Levels = strawberry, orange, and banana
Answers
The factor and levels in the scenario is,
Factor = dip flavor. Levels = strawberry, orange, and banana.
What is popsicles?
A frozen treat on a stick made of liquid is known as an ice pop. An ice pop is "quiescently" frozen, or frozen when at rest, and turns into a solid block of ice, unlike ice cream or sorbet, which are churned while freezing to prevent ice crystal formation. It is held by the stick, which serves as a handle.
There is only one factor (independent variable) involved in above case, i.e. dip flavor is only factor mentioned in given case.
We can see that dip flavor has three categories or levels, i.e. strawberry, orange, and banana
Therefore, we have
factor = dip flavor and levels = strawberry, orange, and banana.
To know more about popsicles, click on the link
https://brainly.com/question/28281941
#SPJ4
i need help with this pls :)

Answers
[] 10x + 4
(5x) + (2x + 5) + (3x - 1)
5x + 2x + 3x + 5 - 1
10x + 4
[] 4x + 4
Bottom: (1/2) * (3x -1) = 1/2x - 1/2
Left side: (1/2) * (5x) = 5/2x
Right side: (1/2) * (2x+5) = x + 5/2
\/
Add them together:
(x + 5/2) + (5/2x) + (1/2x - 1/2)
x + 5/2x + 1/2x + 5/2 - 1/2
4x + 4
[] The Triangle Midsegment Theorem (midsegment = 1/2 times triangle base) and then calculated by adding the three midsegments together.
Hope this helps and is correct, have a nice day! :D
check attached file for a diagram I made
Note: I realized after it was made I did the midsegment wrong so ignore that part! It should be a triangle with the three points in the middle of the sides.

The measure of an angle is 74° what is the measure of its complementary angle
Answers
Answer:
16 degrees
Step-by-step explanation:
Complementary angles = 90 degrees
If the measure of one angle is 74 degrees, that means that the measure of the other angle that is complementary to it is 16 degrees.
74 + x = 90
x = 16
Raoul says that Function B has a greater initial value. Is Raoul correct?

Answers
Answer:
yes he is correct because if you where to graph B it would have a greater slope
Step-by-step explanation:
Please hurry!!
What is the slope of the line that contains the points negative 3, negative seven halves and (2, −4)?
one fourth
one tenth
negative one tenth
negative one fourth
Answers
Answer:
0.7
Step-by-step explanation:
This question tests on the concept of slope or gradient of a line.
We know that the equation, m, for a slope =
\( \frac{y2 - y1}{x2 - x1} \)
We can identify 2 points from the question as (x1, y1) and (x2, y2) to solve for the gradient, and therefore they are:
(x1,y1) as (-3,-7.5)
(x2,y2) as (2,-4)
Now we can substitute these values in to solve for the slope.
\( \frac{ - 4 - ( - \frac{7}{2})}{2-(-3)} \\ = \frac{ - 4 + frac{7}{2}}{5} \\ = \frac{-0.5}{5} \\ = - \frac{1}{ 10} \\ = -0.1\)
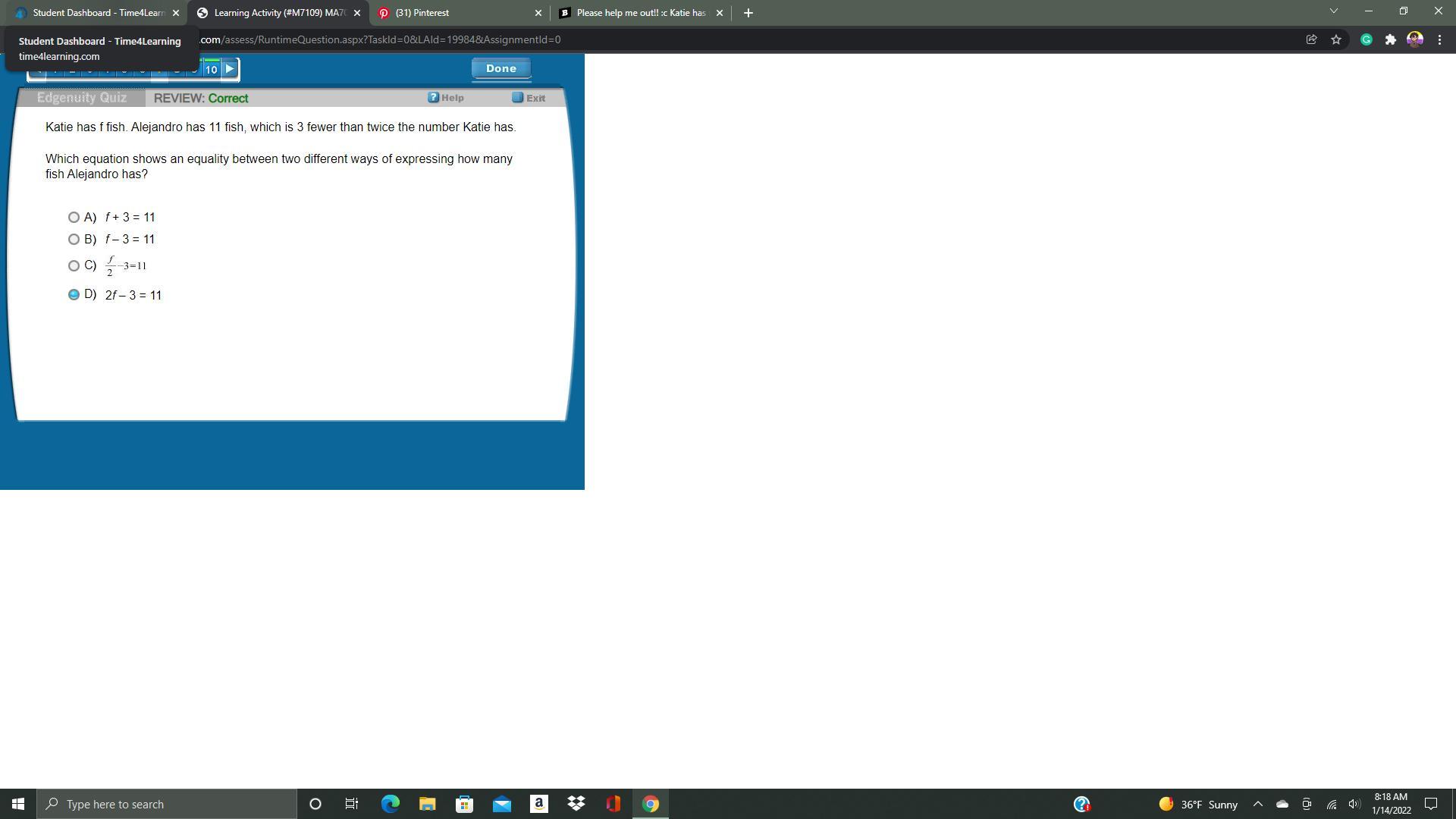
Please help me out!! :c
Katie has f fish. Alejandro has 11 fish, which is 3 fewer than twice the number Katie has.
Which equation shows an equality between two different ways of expressing how many fish Alejandro has?
A. f + 3 = 11
B. f – 3 = 11
C. f/2 - 3 = 11
D. 2f – 3 = 11
Answers
Answer:
The answer would be D
Step-by-step explanation:
To find how many Katie has, you would have to double it ( times by 2 ). Then subtract 3, since Alejandro has three less than twice as many as Katie.
Answer:
the answer is d just did the test got it right
Step-by-step explanation:
the refrigerators at Hal's discount appliances are 30% off the original price during the 12th anniversary spectacular.MR Hanson is shopping for a new refrigerator and has a coupon for a 12% discount off the sale price.if the original price of a refrigerator is 1249 how much will MR.Hanson pay for the refrigerator before tax
Answers
Answer:
$769.38
Step-by-step explanation:
First, find the cost with the 30% off original price:
1249(0.7)
= 874.3
Now, find the cost with the 12% discount off sale price:
874.3(0.88)
= 769.38
So, Mr Hanson would pay $769.38 before tax
Answer:
$769.38
Step-by-step explanation:
Original price: $1249
100% - 30% = 70%
A 30% discount means that you pay 70% of the amount.
Apply a 30% discount: 0.70 * $1249 = $874.30
100% - 12% = 88%
A 12% discount means that you pay 88% of the amount.
Apply a 12% discount: 0.88 * $874.30 = $769.384
Answer: $769.38
3x+4y=36
Y=-1/2+8
How do I solve this?
Answers
Answer:
x = 2
Step-by-step explanation:
3x+4y=36
Y=-1/2+8
Now we substitute y with -1/2+8.
3x + 4(-1/2+8) = 36
3x + 4(7.5) = 36
3x + 30 = 36
3x = 6
x = 2
Have an amazing day!!
Please rate and mark brainliest!
Find the missing number

Answers
If the exterior angles of a convex octagon are x +12, 2x-3, 3x +10, 3x +15, 2x - 19, 4x-1, 4x - 10, and 6x, calculate the largest of the eight angles.
Answers
Answer: Largest exterior angle is 85.44 degrees
===========================================================
Explanation
Rule: The exterior angles of any polygon always add to 360 degrees
Based on that rule, we simply add up the 8 expressions given to us and set that sum equal to 360. Then we solve for x
(x+12)+(2x-3)+(3x+10)+(3x+15)+(2x-19)+(4x-1)+(4x-10)+(6x) = 360
(x+2x+3x+3x+2x+4x+4x+6x)+(12-3+10+15-19-1-10) = 360
25x+4 = 360
25x = 360-4
25x = 356
x = 356/25
x = 14.24
-------------------------------------
Once you determine the value of x, you plug that into each of the 8 exterior angle expressions
x+12 = 14.24+12 = 26.242x-3 = 2(14.24)-3 = 25.483x+10 = 3(14.24)+10 = 52.723x+15 = 3(14.24)+15 = 57.722x-19 = 2(14.24)-19 = 9.484x-1 = 4(14.24)-1 = 55.964x-10 = 4(14.24)-10 = 46.966x = 6*(14.24) = 85.44In short we have these 8 exterior angles
x+12 = 26.242x-3 = 25.483x+10 = 52.723x+15 = 57.722x-19 = 9.484x-1 = 55.964x-10 = 46.966x = 85.44We see that 85.44 degrees is the largest exterior angle (which is the angle that corresponds to the 6x). This makes sense because the 6 is the largest x coefficient compared to something like 2x-3 or 3x+10 which have x coefficients of 2 and 3 respectively.
Which is the minimum SOP expression for the function f(x, y, z) = xyz + xyz + xyz'? Partial credit is granted for incomplete simplifications x'yz + xy y xyz + y xy + yz Which is the minimum SOP expression for the function F(X, Y, Z) = (X + Y') Z + (XZ) + Y? Partial credit is granted for incomplete simplifications. XY' + Z' + Y X + Y X + Y + Z'
Answers
Minimum SOP expression of the given Boolean function F(X, Y, Z) is given as XY' + Z' + YX + YX + Y + Z.
Minimum SOP expression for the function f(x, y, z)
The given Boolean expression of f(x, y, z) is
f(x, y, z) = xyz + xyz + xyz’
Using the Boolean property of the distributive law and combining the common term xyz, we get
f(x, y, z) = xyz + xyz + xyz’= xyz + xyz’= xz(y + y’)
= xz·1
= xz
Minimum SOP expression of the given Boolean function f(x, y, z) is xz.
Minimum SOP expression for the function F(X, Y, Z)
The given Boolean expression of F(X, Y, Z) is
F(X, Y, Z) = (X + Y') Z + (XZ) + Y
Using the Boolean property of the distributive law and combining the common term XZ, we get
F(X, Y, Z) = (X + Y') Z + (XZ) + Y= XZ + YZ' + XYZ' + XY + Y
= XY'Z' + XYZ' + XY + Y+ XZ (since Y + Y’ = 1)
Again using the Boolean property of the distributive law, we get
F(X, Y, Z) = XY'Z' + XYZ' + XY + Y + XZ= XY'Z' + XYZ' + XZ + XY + Y
The Boolean expression obtained is a Sum of Products (SOP).
Minimum SOP expression of the given Boolean function F(X, Y, Z) is given as XY' + Z' + YX + YX + Y + Z.
To know more about Boolean function visit:
https://brainly.com/question/27885599
#SPJ11
Answer this ASAP, I will give the brainliest answer.
Given that y = 4 cm and θ = 38°, work out x rounded to 1 DP.
The diagram is not drawn accurately.

Answers
from S^OH
sinθ=opp/hyp
sin38°=x/4
cross multiply and make x the subject of the formulax=4sin38°
x=4×(0.61566147533)
x=(2.4626459013)
to 1dp
x=2.5cm
A resistor dissipates 1.90 w when the rms voltage of the emf is 11.0 v . part a at what rms voltage will the resistor dissipate 12.0 w
Answers
Therefore, the rms voltage at which the resistor will dissipate 12.0 W is 24.97 V. It's important to note that this value is the rms voltage, which represents the effective or equivalent voltage of an AC signal.
To solve this problem, we can use the formula for power dissipated by a resistor: P = V^2/R, where P is the power, V is the voltage, and R is the resistance. We are given P = 1.90 W and V = 11.0 V, so we can solve for R: R = V^2/P = (11.0 V)^2/1.90 W = 64.74 ohms.
To find the voltage at which the resistor dissipates 12.0 W, we can rearrange the formula to solve for V: V = sqrt(P*R). Plugging in P = 12.0 W and R = 64.74 ohms, we get V = sqrt(12.0 W * 64.74 ohms) = 24.97 V (rounded to three significant figures).
To know more about voltage visit:
https://brainly.com/question/31347497
#SPJ11
Please answer this math question for me

Answers
Answer:
Hello! answer: e = 103 f = 77
and I don't really know what d is sorry! but If I had to guess id say 90
The value of a certain car after one year was $13,595. The value of the same car after 3 years was $11,095. Find the slope and explain what it means.
Answers
Answer:
-1250/1 or -1250
This tells us that the car depreciated in value by $1250 every year.
Step-by-step explanation:
11,095-13,595= -2500
This is the value that the car has depreciated over 2 years (from the first year to the third year)
Since we need to find the slope we divide this value by two.
That value would be -1250
Since the value is negative, we know the car has depreciated in value. We also now know that it depreciated in value by $1250 every year
Hope this helps!
Consider three points A(1, 2), B(4, 5), and C(2, -1).
a Find the equation of the perpendicular bisector of:
i [AB]
ii [AC]
iii [BC]
b Graph the three perpendicular bisectors on the same set of axes. Discuss your observations.
c Describe how you can find the centre of the circle which passes through three non-collinear
points.
Answers
Answer:
⊥ to AB : x +y = 6
⊥ to AC : x -3y = 0
⊥ to BC : x +3y = 9
see the attachment for a graph
Step-by-step explanation:
You want the equations and graphs of the perpendicular bisectors of AB, BC, and AC where the points are A(1, 2), B(4, 5), and C(2, -1). You want to relate this to finding the center of a circle through three non-collinear points.
Perpendicular bisectorThe perpendicular bisector of a segment PQ with P(x1, y1) and Q(x2, y2) can be written as ...
(x2-x1)(x -(x1+x2)/2) +(y2-y1)(y -(y1+y2)/2) = 0
(a) EquationsApplying this to the given segments, we have ...
⊥ to AB : (4 -1)(x -(4+1)/2) +(5 -2)(y -(5+2)/2) = 0 ⇒ x +y = 6
⊥ to AC : (2 -1)(x -(2+1)/2) +(-1 -2)(y -(-1+2)/2) = 0 ⇒ x -3y = 0
⊥ to BC : (2 -4)(x -(2+4)/2) +(-1 -5)(y -(-1+5)/2) = 0 ⇒ x +3y = 9
(b) GraphThe attachment shows a graph of the lines and their single point of intersection.
Each perpendicular bisector is the locus of the centers of circles through the end points of the respective segments. Then the intersection of those bisectors is the center of a circle through all of the points.
Solving any pair of these equations simultaneously gives the circle center as (4.5, 1.5). This is point D on the graph.
(c) DiscussionThe given points are non-collinear, and the intersection of the perpendicular bisectors is the center of a circle through them. The method described in this problem is a suitable method for finding the circle center. (If the three points are considered a triangle, this center is called the "circumcenter.")
__
Additional comment
We have written the equations for the lines in standard form, with a positive leading coefficient and mutually prime integers. You will notice the graphing program wrote the same equations for those lines.

a lawyer researched the average number of years served by 45 different justices on the supreme court. the average number of years served was 13.8 years with a standard deviation of 7.3 years. what is the 95% confidence interval estimate for the average number of years served by all supreme court justices? place your limits, rounded to 1 decimal place,
Answers
"a lawyer researched the average number of years served by 45 different justices on the supreme court. the average number of years served was 13.8 years with a standard deviation of 7.3 years.
The 95% confidence interval estimate for the average number of years served by all supreme court justices is [11.2, 16.4].According to the central limit theorem , a sampling distribution of the means is usually distributed in a normal distribution, given a big enough sample size, which means that it has a bell-shaped curve. It has a standard deviation that can be estimated by dividing the population standard deviation by the square root of the sample size. Using the formula below,
we can calculate the 95% confidence interval for the population average.= 13.8 ± (1.96 × 7.3 / √45)
= 13.8 ± (1.96 × 1.088)
= 13.8 ± 2.13The limits are calculated by adding and subtracting the calculated value from the sample mean.13.8 + 2.13
= 15.9313.8 - 2.13
= 11.67Therefore, the 95% confidence interval estimate for the average number of years served by all supreme court justices is [11.2, 16.4].
To know more about average, visit:
https://brainly.com/question/24057012
#SPJ11
A is an n times n matrix. Check the true statements below: If Ax = lambda x for some vector x , then lambda is an eigenvalue of A . A number c is an eigenvalue of A if and only if the equation (A-cI)x=0 has a nontrivial solution x . Finding an eigenvector of A might be difficult, but checking whether a given vector is in fact an eigenvector is easy. To find the eigenvalues of A , reduce A to echelon form. A matrix A is not invertible if and only if 0 is an eigenvalue of A .
Answers
The true statements are as follows: If Ax = λx for some vector x, then λ is an eigenvalue of A. This is the definition of an eigenvalue and eigenvector relationship.
A number c is an eigenvalue of A if and only if the equation (A-cI)x = 0 has a nontrivial solution x. This is equivalent to saying that c is an eigenvalue if and only if (A-cI) is singular, meaning it has a nontrivial null space.
Finding an eigenvector of A might be difficult, but checking whether a given vector is an eigenvector is easy. This is because to check if a vector is an eigenvector, we simply need to verify if Ax = λx holds, which involves straightforward matrix-vector multiplication.
To find the eigenvalues of a matrix A, reducing A to echelon form is not a direct method. The eigenvalues of a matrix are determined by solving the characteristic equation det(A - λI) = 0, where I is the identity matrix. The characteristic equation gives a polynomial equation in λ, and the solutions to this equation are the eigenvalues of A.
Lastly, it is incorrect to state that a matrix A is not invertible if and only if 0 is an eigenvalue of A. While it is true that an invertible matrix does not have 0 as an eigenvalue, the converse is not always true. There are non-invertible matrices that also have 0 as an eigenvalue. Invertibility is determined by the rank of the matrix, not solely by the presence of 0 as an eigenvalue.
To learn more about matrix-vector multiplication click here:
brainly.com/question/13006202
#SPJ11