1. What is 47% of 268?
Answers
Answer:
125.96
Step-by-step explanation:
47 x 268 divided by 100
= 125.96
Related Questions
Average rate of change from G from x=1 to x=4 is
Answers
Answer:
3
Step-by-step explanation:
minus the variable, 4-1 is 3.
In 1995, wolves were introduced into Yellowstone Park.
The function `w\left(x\right)=14\cdot1.08^{x}` models the number of wolves, `w`, in the years since 1995, `x`.
Determine the value of `w(25)`.
What does this value say about the wolf population?
Answers
Answer:
w(25) = 96
There are 96 wolves in the year 2020
Step-by-step explanation:
Given:
\(w(x)=14\cdot 1.08^{x}\)
w(25) =
\(w(25)=14\cdot 1.08^{25}\\\\= 14 * (6.848)\\\\=95.872\\\\\approx 96\)
Number of years : 1995 + 25 = 2020
In 2020, there are 96 wolves
Suppose 47G% of the doctors in a hospital are surgeons. If a sample of 460460 doctors is selected, what is the probability that the sample proportion of surgeons will differ from the population proportion by greater than 5%5%
Answers
Answer:
3.16% probability that the sample proportion of surgeons will differ from the population proportion by greater than 5%
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal probability distribution
When the distribution is normal, we use the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1-p)}{n}}\)
In this question:
\(p = 0.47, n = 460, \mu = 0.47, s = \sqrt{\frac{0.47*0.53}{460}} = 0.0233\)
What is the probability that the sample proportion of surgeons will differ from the population proportion by greater than 5%
Sample proportion lower than 0.47 - 0.05 = 0.42 or higher than 0.47 + 0.05 = 0.52.
Since they are equidistant from the mean of 0.47 they are equal. So we find one of them, and multiply by two.
Lower than 0.42:
pvalue of Z when X = 0.42. So
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{0.42 - 0.47}{0.0233}\)
\(Z = -2.15\)
\(Z = -2.15\) has a pvalue of 0.0158
2*0.0158 = 0.0316
3.16% probability that the sample proportion of surgeons will differ from the population proportion by greater than 5%
Convert each measurement
18 meters = ??? centimeters

Answers
Answer:
18 meters = 1800 milimeters
Step-by-step explanation:
Hope this helps! :3
plz mark as brainliest!
Answer:
Just search it up. The answer is 1800
Step-by-step explanation:
Type.
Or there's another way.... you multiply if you want to convert a unit that is greater to smaller, and you divide if you want to convert a smaller unit to a larger one.
For example hours to minutes:
You cross out the word that matches. Here it's hour.
3.15 hours X 60 min/1 hour=189 min
189min X 60 sec/1min=11340 sec
and if it's from smaller to greater you divide, get it?
what is 5(2x - 2y) - (4x + 3y)
Answers
Answer:
6x - 13y
Step-by-step explanation:
5(2x - 2y) - (4x + 3y)
10x - 10y - 4x - 3y
10x - 4x - 10y - 3y
6x - 13y
PLEASE HELP WILL MARK BRAINLIEST..Write a polynomial function of least degree with rational coefficients so that P(x) = 0 has the given roots.
x= -2, x=7
P(x)=

Answers
A polynomial function of least degree with rational coefficients so that P(x) = 0 has the given roots is P(x)=x²-5x-14
What is a polynomial function?A function is said to as polynomial when a variable in an equation, such as a quadratic equation or cubic equation, etc., has only positive integer exponents or non-negative integer powers. One polynomial with an exponent of 1 is 2x+5, for instance. One that has more than two algebraic terms is referred to as a polynomial expression. Polynomial is a monomial or binomial that is repeatedly added, as the name suggests.
A mathematical expression containing one or more algebraic terms, where each algebraic term is made up of a constant multiplied by one or more variables raised to a nonnegative integral power.
x= -2, x=7
Given,
P(x) = 0
This polynomial function has the roots,
x= -2, x=7
So,
(x+2)(x-7)
We have to multiply both of them we get,
P(x)=(x+2)(x-7)
0=x²-5x-14
x²-5x-14=0
Therefore, P(x)=x²-5x-14 is the polynomial function.
To know more about polynomial function, visit:
https://brainly.com/question/12976257
#SPJ1
Work out the length of x. Give your answer rounded to 3 significant figures. 13.3 mm 5.5 mm The diagram is not drawn accurately. X = 0 mm x
Answers
Step-by-step explanation:
Based on the information given, we have a diagram with two sides labeled as 13.3 mm and 5.5 mm, and another side labeled as X mm.
To find the length of X, we can use the fact that the sum of the lengths of the sides of a triangle is equal to the perimeter.
Perimeter = 13.3 mm + 5.5 mm + X mm
The perimeter is the total distance around the triangle. Since we have three sides, the perimeter is the sum of the lengths of those sides.
To find X, we can subtract the sum of the known sides from the perimeter:
X mm = Perimeter - (13.3 mm + 5.5 mm)
Since the value of X is not given, we cannot calculate it without the perimeter value. If you provide the perimeter value, I can help you find the length of X.
Bob is taking Jill out to dinner. Their bill was $27.50. If Bob spent a total of $32.45 including the tip what was the
percentage of the tip?
Answers
Step-by-step explanation:
100% = $27.50
1% = 100%/100 = $27.50/100 = $0.275
the extra amount paid (for the tip) was
$32.45 - $27.50 = $4.95
to know how many percent that is, we need to see how often 1% fits into that amount.
so,
4.95 / 0.275 = 18
therefore the tip was 18%.
FYI - in real life the tip percentage (and corresponding amount) is calculated based on the net bill (the amount before sales tax).
factor and solve
x^2-4x=5
Answers
Let’s solve the equation x^2 - 4x = 5 by factoring:
First, we’ll move all the terms to one side of the equation:
x^2 - 4x - 5 = 0
Now, we’ll factor the left side of the equation. We’re looking for two numbers that multiply to -5 and add to -4. Those numbers are -5 and 1. So we can write:
(x - 5) (x + 1) = 0
Now we’ll use the zero-product property to solve for x. This property states that if the product of two numbers is zero, then at least one of the numbers must be zero. So we have:
x - 5 = 0 or x + 1 = 0
Solving each equation separately, we find that x = 5 or x = -1.
So, the solutions to the equation x^2 - 4x = 5 are x = 5 and x = -1.
Suppose we are minimizing the objective function value of a linear program. The feasible region is defined by 5 corner points. The objective function values at the five corner points are 4, 11, 7, 4, and 10. What type of solution do we have for this problem?.
Answers
The linear program shows that there are different attainable arrangements that accomplish the same ideal objective function value..
How to determine the solution to the objective function value of a linear programBased on the given data, since the objective function values at the five corner points are diverse, able to conclude that there's no one-of-a-kind ideal arrangement for this linear program.
The reality that there are numerous distinctive objective function values at the corner points suggests that there are numerous ideal arrangements or that the objective work isn't maximized or minimized at any of the corner points.
In this case, the linear program may have numerous ideal arrangements, showing that there are different attainable arrangements that accomplish the same ideal objective function value.
Learn more about Objective function value here:
https://brainly.com/question/14309521
#SPJ1
Solve for b. d = abc

Answers
3. Figure ABCD Shown below is
made up of a semlore and a
rectangle. O is the contre of the
line DC
(Use
- )
10 cm
Calculate the area of
anglo AOB
Answers
Answer:
In a rectangle ABCD of 3 mx 4 m, starting from A and D, along the sides AB and DC after every 30 cm, a square shape of 10 cm is taken out as shown below. What will be the perimeter (in cm)
Step-by-step explanation:
12 CM And 300 CM is the answer
Two student clubs were selling t-shirts and school notebooks to raise money for an upcoming school event. In the first few minut
notebooks, and made $19. Club B sold 1 t-shirt and 1 notebook, for a total of $8.
-
Use matrices to solve the equation and determine the cost of a t-shirt and the cost of a notebook. Show or explain all necessary:

Answers
Using matrices the simultaneous equation is solved to get x = 3 and y = 5
How to solve the simultaneous equation using matricesThis method required finding determinants in three occasions then dividing
The given equation
\(\left[\begin{array}{cc}3&2&\\1&1\\\end{array}\right] \left[\begin{array}{c}x\\y\\\end{array}\right]= \left[\begin{array}{c}19\\8\\\end{array}\right]\)
the determinant is
\(\left[\begin{array}{cc}3&2&\\1&1\\\end{array}\right]\)
3 * 1 - 2 * 1 = 3 - 2 = 1
Solving for x
determinant while replacing x values
\(\left[\begin{array}{cc}19&2&\\8&1\\\end{array}\right]\)
19 * 1 - 2 * 8 = 19 - 16 = 3
solving for x = 3/1 = 3
Solving for y
determinant while replacing y values
\(\left[\begin{array}{cc}3&19&\\1&8\\\end{array}\right]\)
3 * 8 - 19 * 1 = 24 - 19 = 5
solving for y = 5/1 = 5
Learn more about simultaneous equations at:
https://brainly.com/question/148035
#SPJ1
F(x)=(x-2)(x-6) Find the x-intercepts
Answers
how many yards are 2 miles and 30 feet
Answers
Hey there!☺
\(Answer:\boxed{3,530}\)
\(Explanation:\)
2 miles = 3,520 yards
30 feet = 10 yards
Add up both.
\(3,520+10=3,530\)
3,530 is your answer.
Hope this helps!☺
The number of yards for 2 miles and 30 feet by unit conversion is given by the relation A = 3530 yards
Given data ,
Let the total number of yards be represented as A
Now, the value of A is
The initial number of miles = 2 miles
where 1 mile = 1760 yards
So , 2 miles = 3520 yards
From the unit conversion , we get
30 feet = 10 yards
So , the total number of yards A = 3520 + 10
On simplifying the equation , we get
A = 3530 yards
Hence , the unit conversion is solved and total yards = 3530 yards
To learn more about unit conversion click :
https://brainly.com/question/19420601
#SPJ6
solve the equation -16=a- 19
Answers
Answer:
a = 3
Step-by-step explanation:
Collect like-terms:
\( - 16 = a - 19\)
\(a = - 16 + 19\)
\(a = 3\)
Answer: 3
Step-by-step explanation: you take 19 from 3 giving you -16
pls help bro
pls help bro
pls halp bro

Answers
Answer:
–6.4z – 3.5xz
Step-by-step explanation:
Apply the distributive property:
The distributive property lets you multiply a sum by multiplying each addend separately and then add the products.
In this case we have to multiply each term (-6.4 and -3.5x) by z, then add both.
z(–6.4 – 3.5x)
-6.4(z)-3.5x(z)
–6.4z – 3.5xz
Solve for X
6x+60x+150=0
Answers
Answer:
x = -2.27272727273in fractionx = -25/11
Step-by-step explanation:
Solve for X
6x+60x+150=0
66x = -150
x = -150 : 66
x = -2.27272727273
in fraction
x = -25/11
Find the formula for the nth term of the following sequence:
17, 28, 39, 50...
Answers
Answer: 17, 28, 39, 50, ..., 11n+6
Step-by-step explanation:
17, 28, 39, 50, ...
28-17=11
39-28=11
50-39=11
Hence,
This is an arithmetic progression where a₁=17 and d=11
Use the formula for an arithmetic progression:
\(a_n=a_1+(n-1)d\\a_n=17+(n-1)11\\a_n=17+11n-11\\a_n=11n+6\)
A spinner with 10 equal sized slices has 4 yellow slices, 3 red, and 3 blue slices. Kala spun the dial 1000 times and got the following results.
Answers
Kala spun the spinner 1000 times and got the following results:
- Yellow: 400 times
- Red: 300 times
- Blue: 300 times
1. Calculate the amount of sales tax:
- The item costs $350 before tax.
- The sales tax rate is 14%.
- To find the sales tax amount, multiply the cost of the item by the tax rate:
Sales tax = $350 * 0.14 = $49.
2. Determine the total cost of the item including tax:
- Add the sales tax amount to the original cost of the item:
Total cost = $350 + $49 = $399.
3. Analyze the spinner results:
- The spinner has 10 equal-sized slices.
- There are 4 yellow slices, 3 red slices, and 3 blue slices.
- Kala spun the dial 1000 times.
4. Calculate the frequency of each color:
- Yellow: Kala got 400 yellow results out of 1000 spins.
- Red: Kala got 300 red results out of 1000 spins.
- Blue: Kala got 300 blue results out of 1000 spins.
5. Calculate the probability of landing on each color:
- Yellow: Probability = Frequency of yellow / Total spins = 400 / 1000 = 0.4.
- Red: Probability = Frequency of red / Total spins = 300 / 1000 = 0.3.
- Blue: Probability = Frequency of blue / Total spins = 300 / 1000 = 0.3.
For more such questions on spinner, click on:
https://brainly.com/question/32737567
#SPJ8
What is the surface area of the box formed by the pattern below?

Answers
Answer:
S.A = 2( L×W+W×H+ H×L)
= 2(2×4+4×1+1×2)
= 2(8+4+2)
2(14)
= 2×14= 28
Step-by-step explanation:
answer 28
The slope of a line is 0, and the y-intercept is 6. What is the equation of the line written in slope-intercept form?
O y=6x
Oy=6
O y=x+6
Answers
Answer:
The correct answer is y = x + 6
4. Water has a boiling point of 100 degrees Celsius, a melting point of 0 degrees celsius, and density of 1 g/cm. What is this a list of?
•chemical properties
•unimportant details
•physical properties
•incorrect facts
Answers
Answer:C
Step-by-step explanation:
Two UNO students want to start a business selling slushies at the Gene Leahey Mall during the summer. They will have an initial cost of $500 to buy equipment and an additional $1.25 cost for each slushie they sell. They
plan to charge $3.50 for each slushie. Let C(x) represent the cost (in dollars) associated with starting and running the business and R(x) represent the revenue (in dollars) earned from sales. Let x represent the number
of slushies sold.
a. Write a linear function for cost.
C(x) =
b. Write a linear function for revenue.
R(x) =
Answers
Part (a)
The cost is the initial cost plus the cost per slushie multiplied by the number of slushies sold.
\(C(x)=500+1.25x\)
Part (b)
The revenue is the number of slushies sold multiplied by the amount charged per slushie.
\(R(x)=3.50x\)
The sum of three consecutive terms of an arithmetic sequence is 27, and the sum of their squares is 293. What is the absolute difference between the greatest and the least of these three numbers in the arithmetic sequence?
The answer is 10 but I don’t know how to get it
Answers
The absolute difference between the greatest and the least of these three numbers in the arithmetic sequence is 10.
The sequence is an arithmetic sequence. Therefore,
d = common difference
let
a = centre term
Therefore, the 3 consecutive term will be as follows
a - d, a, a + d
a - d + a + a + d = 27
3a = 27
a = 27 / 3
a = 9
Therefore,
(a-d)² + (a)² + (a + d)² = 293
(a²-2ad+d²) + 9² + (a² + 2ad + d²) = 293
(81 - 18d + d²) + 81 + (81 + 18d + d²) = 293
243 + 2d² = 293
2d² = 50
d² = 50 / 2
d = √25
d = 5
common difference = 5
Therefore, the 3 numbers are as follows
9 - 5 , 9, 9 + 5 = 4, 9, 14
The difference between the greatest and the least of these 3 numbers are as follows:
14 - 4 = 10
learn more on Arithmetic progression: https://brainly.com/question/25749583?referrer=searchResults
f(x) = 2x + 3 and
g(x) = -3x + 1
f(4) + g(-2)=?
Answers

the center of a semisimple lie algebra {\displaystyle {\mathfrak {g}}}{\mathfrak {g}} is trivial proof. t/f
Answers
Answer:
False. The center of a semisimple Lie algebra is usually not trivial.
Step-by-step explanation:
The center of a semisimple Lie algebra is the set of elements of the Lie algebra that commute with all other elements in the algebra. In most cases, the center of a semisimple Lie algebra is not trivial, meaning it contains at least one non-zero element. For example, the center of the simple Lie algebra sl(2,C) contains the two-dimensional Lie algebra spanned by the scalar matrices I and -I. The center of the Lie algebra so(5,C) is spanned by the five-dimensional Lie algebra spanned by the matrices diag(1,1,1,-1,-1). These examples demonstrate that the center of a semisimple Lie algebra is usually not trivial.
To read more above Lie algebra questions, ref:
https://brainly.com/question/12154047?referrer=searchResults
#SPJ4
if a company receives 13,300 from a client for services provided the effect on the accounting equation would be
Answers
Based on the fact that the company received 13,300 currency units from a client, the effect on the accounting equation would be increase in assets and increase in equity.
What is the change in the accounting equation?The accounting equation is:
Assets = Equity + Liabilities
The 13,300 currency units would count as cash which is an asset so assets will increase by the amount of $13,300.
The same $13,300 will also count as revenue as the company receives it for services rendered so the revenue will increase. Revenue is an equity account so Equity will increase.
Find out more on the accounting equation at https://brainly.com/question/24401217
#SPJ1
The parent square root function, f, is transformed to create function g.g(x) = √x +3 - 4Which statement is true?

Answers
The parent function f is given by:
\(f(x)=\sqrt{x}\)Translating the function horizontally 3 units to the left gives a new function h:
\(h(x)=\sqrt{x+3}\)Translate the new function h vertically up by 4 units to get g:
\(g(x)=\sqrt{x+3}-4\)Therefore, the correct choice is:
Are the two triangles similar? How do you know?
A.)no
B.)yes; by AA
C.)yes; by SAS
D.)yes; by SSS
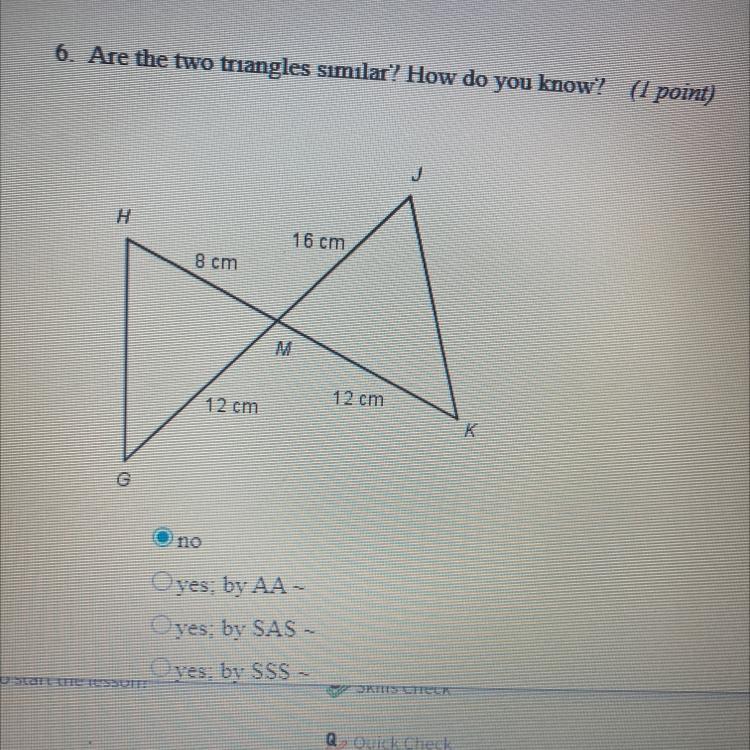
Answers
Answer:
No
Step-by-step explanation:
At least two sides will have to be the same.