1) The endpoints of FCare (-2,-4 and G(1,0). Find the length of FG-
Answers
Answer:
it is \(5\)
Related Questions
What is the value of b?
10
16
20
26
y’all know ??
Answers
Answer:
a
Step-by-step explanation:
on edge 21
The value of {b}, that is the slope of the line is equivalent to 1/9.
What is the general equation of a straight line?The general equation of a straight line is → y = mx + c.
[m] is slope of line.[c] is the y - intercept.Given is a graph as shown in the image attached.
The given line has the coordinates mentioned below -
A(7, 22)
B(25, 24)
We can write the slope as -
{m} = (y₂ - y₁)/(x₂ - x₁)
{m} = (24 - 22) (25 - 7)
{m} = 2/18
{m} = 1/9
Therefore, the value of {b}, that is the slope of the line is equivalent to 1/9.
To solve more questions on straight lines, visit the link below -brainly.com/question/29149364
#SPJ5
Find the area enclosed by y = 3x and y=x^2. Round your answer to one decimal place.
Answers
The area enclosed by the curves y = 3x and \(y = x^2\) is 13.5 square units (rounded to one decimal place).
To find the area enclosed by the curves y = 3x and \(y = x^2\), we need to find the points of intersection and integrate the difference between the curves with respect to x.
First, we find the points of intersection by setting the two equations equal to each other:
\(3x = x^2x^2 - 3x = 0x(x-3) = 0x = 0 or x = 3\)
So the curves intersect at the points (0,0) and (3,9).
To find the area enclosed between the curves, we integrate the difference between the curves with respect to x from x=0 to x=3:
Area =\(\int\limits (y = x^{2} \ to\ y = 3x) dx\) from 0 to 3
= \(\int\limits(3x - x^2) dx \ from \ 0 \ to \ 3\)
= \([3/2 x^2 - 1/3 x^3] from 0 to 3\)
= (27/2 - 27/3) - (0 - 0)
= 13.5 square units
Therefore, the area enclosed by the curves y = 3x and \(y = x^2\) is 13.5 square units (rounded to one decimal place).
To know more about area refer here:
https://brainly.com/question/27683633
#SPJ11
Given the following pdf;
f(x) = (3x+17)/73.5, for 1 < x < 4
What is the probability that x falls between 0.2 below its mean and 0.4 above its mean?
A. ~0.115
B. ~0.305
C. ~0.335
D. ~0.350
E. ~0.250
Answers
The probability that x falls between 0.2 below its mean and 0.4 above its mean is approximately 0.115, or option A.
To solve this problem, we need to first find the mean of the probability distribution. We can do this by using the formula for the mean of a continuous probability distribution:
μ = ∫xf(x)dx
where the integral is taken over the entire range of the distribution. In this case, since the range is from 1 to 4, we have:
μ = ∫1^4 (3x+17)/73.5 dx
μ = [3/2 * x^2/73.5 + 17/73.5 * x] from 1 to 4
μ = (3/2 * 16/73.5 + 17/73.5 * 4) - (3/2 * 1/73.5 + 17/73.5 * 1)
μ = 2.5
So the mean of the distribution is 2.5.
Next, we need to find the probability that x falls between 0.2 below its mean and 0.4 above its mean. We can do this by using the cumulative distribution function (CDF):
P(2.3 < x < 2.9) = ∫2.3^2.9 f(x)dx
P(2.3 < x < 2.9) = ∫2.3^2.9 (3x+17)/73.5 dx
P(2.3 < x < 2.9) = [(3/2 * x^2/73.5 + 17/73.5 * x)] from 2.3 to 2.9
P(2.3 < x < 2.9) = [(3/2 * 8.41/73.5 + 17/73.5 * 2.9) - (3/2 * 5.29/73.5 + 17/73.5 * 2.3)]
P(2.3 < x < 2.9) = 0.115 (approximately)
Therefore, the probability that x falls between 0.2 below its mean and 0.4 above its mean is approximately 0.115, or option A.
Visit to know more about Probability:-
brainly.com/question/13604758
#SPJ11
your company is producing special battery packs for the most popular toy during the holiday season. the life span of the battery pack is known to be normally distributed with a mean of 250 hours and a standard deviation of 20 hours. what would typically be a better distribution than the normal distribution to model the life span of these battery packs?
Answers
In order to determine whether the Weibull distribution or another distribution might be a better fit for the lifespan of these battery packs, it would be important to analyze the data and compare the goodness-of-fit statistics for different distributions.
What is probability?
Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain to happen.
The normal distribution is a very common and useful distribution for modeling many real-world phenomena, including the lifespan of battery packs. However, there are certain situations where other distributions may be more appropriate.
One example of a distribution that could potentially be a better fit for the lifespan of these battery packs is the Weibull distribution. The Weibull distribution is often used to model the failure rates of components, including batteries. It has a flexible shape that can be adjusted to fit different types of failure patterns, and it can handle both increasing and decreasing failure rates.
In order to determine whether the Weibull distribution or another distribution might be a better fit for the lifespan of these battery packs, it would be important to analyze the data and compare the goodness-of-fit statistics for different distributions. This could involve using statistical software to fit various distributions to the data and comparing the resulting fit statistics, such as the Akaike information criterion (AIC) or the Bayesian information criterion (BIC), to determine which distribution provides the best fit.
To learn more about probability from the given link:
https://brainly.com/question/30034780
#SPJ1
answer quick please look at attachment.

Answers
Answer:
c) KJ and JH
Step-by-step explanation:
Answer:
lowkey gonna say B
Step-by-step explanation:
shshevr fcfvdbd
histograms are used to a. determine the distribution of nonresponse errors. b. investigate the relation between two variables. c. construct cumulative distribution functions. d. construct cross tabulation tables. e. determine the empirical distribution of a variable.
Answers
Histograms are used to determine the empirical distribution of a variable. Therefore, option (e) is the correct one.
Histogram is used to summarize discrete or continuous data measured on an interval scale. It is often used to describe key features of the distribution of data in a practical way.
A histogram divides the range of possible values in a data set into different classes or groups. For each group, a rectangle is created with a base length equal to the range of values in that particular group and a length equal to the number of observations that fall into that group.
Histograms are similar to column charts, but there are no gaps between the bars. Histograms generally have equal width bars.
Thus, it can be concluded that histograms are used to determine the empirical distribution of a variable. Therefore, option (e) is the correct one.
To learn more about histogram visit https://brainly.com/question/16819077
#SPJ4
pleas help due to night

Answers
Answer:
72
Step-by-step explanation:
20+20+16+16=72, when they give you half of the sides, the sides opposite of it is the same.
Answer:
72
Step-by-step explanation:
When you are looking for perimeter you add all of the sides so 16+16 and 20+20 then add the sum of each side can I have brainliest please pretty please
Please do this asap, last question on the packet!!

Answers
Answer: c
Step-by-step explanation:
Write the Equation
= 5.5x + 6.2y + 4.3x + 8.3z + 1.6z - 5.1y
Re-arrange them
= 5.5x + 4.3x + 6.2y - 5.1y + 8.3z + 1.6z
Add them
= 9.8x + 0.1y + 9.9z
Please help with my question

Answers
Answer:
what is ur questions we cant see them
An equation is shown below: 6(2x – 11) + 15 = 3x + 12 Part A: Write the steps you will use to solve the equation, and explain each step. (6 points) Part B: What value of x makes the equation true? (4 points)
Answers
Answer: x = 7
Step-by-step explanation:
6(2x-11)+15=3x+12
1) Distribute 6 (distributive-property)
12x - 66 + 15 = 3x + 12
12x - 51 = 3x + 12
Subtract 12 from both sides; what ever you do to one side, you need to do to ther other.
12x - 63 = 3x
Subtract 3x from both sides.
9x - 63 = 0
Add 63 to both sides.
9x = 63
Divide by 9 to getx by itself.
63/9 = 7
x = 7
You wish to test whether an association exists between a categorical variable (such as a rank of a professor at a university, assuming four ranks) and a numerical variable (such as yearly salary).
Answers
To test for an association between a categorical variable and a numerical variable, you can use a statistical method called Analysis of Variance (ANOVA).
In this case, you would use a one-way ANOVA to compare the mean salaries of professors across the four different ranks. This would allow you to determine if there is a significant difference in salary between the different ranks. It is important to note that ANOVA assumes that the numerical variable is normally distributed and that the variances are equal across the different groups. Additionally, post-hoc tests may be necessary to determine which specific groups have significantly different mean salaries. Keep in mind that the sample size and distribution of data can affect the validity of your results. A larger sample size and more normally distributed data will generally result in more accurate conclusions. To test the association between a categorical variable (professor rank with four levels) and a numerical variable (yearly salary), you can use the Analysis of Variance (ANOVA) test. ANOVA helps determine if there are significant differences among the means of different groups (ranks) and if these differences are not due to random chance. If the ANOVA test results show a significant association, it implies that the professor's rank is related to their yearly salary.
To know more about statistical method visit:
https://brainly.com/question/30652356
#SPJ11
One figure models 1/4 as 4 of 12 equal parts of a whole. The other models 1/3 as 1 of 3 equal parts of a whole. What is true about the equal parts for the two fractions?

Answers
The correct option for this questions is Option C
Equivalent Fractions for 4/12:
1/3, 2/6, 3/9, 4/12, 5/15, 6/18, 7/21, 8/24, 9/27, 10/30, 11/33, 12/36, 13/39, 14/42, 15/45, 16/48, 17/51, 18/54, 19/57, 20/60, and so on ...
How do you find equivalent fractions?Two frations are equivalent when they have the same value when written in lowest terms. The fraction 8/24 is equal to 1/3 when reduced to lowest terms. To find equivalent fractions, just multiply the numerator and denominator of that reduced fraction (1/3) by any interger number, ie, multiply by 2, 3, 10, 30.
2/6 is equivalent to 4/12 because 1 x 2 = 2 and 3 x 2 = 63/9 is equivalent to 4/12 because 1 x 3 = 3 and 3 x 3 = 94/12 is equivalent to 4/12 because 1 x 3 = 4 and 3 x 3 = 12Equivalent fractions may look different, but when you reduce then to the lowest terms you will get the same value. If any fraction is not reduced to lowest terms, you can get other equivalent fractions just dividing both numerator and denominator by the same number.
Thus, option c is your answer
Learn more about equivalent fractions here:
https://brainly.com/question/24679788
Is 1.64 rational or irrational?
Answers
Answer:
irrational, I am not that sure tho
Need help with this??? Please!!!

Answers
Answer:
the first option
Step-by-step explanation:
(f-g)(x) simply means to subtract both expressions. really literally.
and we go through it power by power of x.
the highest power/exponent of x is 3 (x³). only f(x) has one.
so, -7x³ is the first part of f-g.
next is x².
11x² - 6x² = 5x², which is the second part of f-g.
next is x.
-8x - (-14x) = -8x + 14x = 6x, which is the third part of f-g.
next is x⁰ (in other words, no x, just a constant).
4 - (-3) = 4 + 3 = 7, which is the 4th part of f-g.
we have no x to the power of -1 or -2, so we have -3
0 - (-4x‐³) = 4x‐³, which is the last part of f-g.
so, it is clearly the first answer option.
A number increased by one third
Answers
Answer:
I would but what is the number dude? just divide the number by 3 and add that to the original number
Step-by-step explanation:
what I just said
Answer: \(\large\boldsymbol{n+\cfrac{1}{3}}\) ✅
\(\stackrel\star{\rightsquigarrow\boldsymbol{\underbrace{Step-by-step\;explanation:}}}\)
Hii, do you need to know the answer to your question? No problem! (:
A number increased by...Let's think about it for a moment. If we increase a number by some other number, we increase its value.
If we increase a number's value, we add something to it.
So "a number increased by one third" is the same as
\(\large\boldsymbol{n+\cfrac{1}{3}}\).
Voila! There's our solution, cheers! (:
--
Hope that this helped! Best wishes.
\(\it Reach\;far.\;Aim\;high.\;Dream\;big.\)
\(\bigstar\underbrace\)
Write and find the general solution of the differential equation that models the verbal statement. (Use k for the proportionality constant.) The rate of change of y with respect to t is inversely proportional to the cube of t.
Answers
The general solution to the differential equation is \(y = (e^{k/(2t^2)})\) / C, where k is the proportionality constant and C is the constant of integration.
The verbal statement implies the following differential equation:
\(dy/dt = -k/t^3\)
To find the general solution, we can separate the variables and integrate both sides.
Separating variables:
\(1/y dy = -k/t^3 dt\)
Integrating both sides:
∫1/y dy = -k ∫\(1/t^3\) dt
\(ln|y| = -k * (-1/2t^2) + C\\ln|y| = k/(2t^2) + C\)
Using the property of logarithms, we can rewrite this as:
\(ln|y| = k/(2t^2) + ln|C|\)
Combining the logarithms:
\(ln|y| = ln|C| + k/(2t^2)\)
We can simplify this further:
\(ln|Cy| = k/(2t^2)\)
Exponentiating both sides:
\(Cy = e^{k/(2t^2)}\)
Finally, we solve for y:
\(y = (e^{k/(2t^2)}) / C\)
where C is the constant of integration.
Therefore, the general solution to the differential equation is \(y = (e^{k/(2t^2)}) / C\).
To know more about differential equation, refer here:
https://brainly.com/question/33150786
#SPJ4
The shelf life of a particular dairy product is normally dstributed with a mean of 12 days and a standard deviation of 3 days.
About what percent of the products last between 12 and 15 days?
Answers
I Agree With person up
:p
how many ways can rudy choose 6 pizza toppings from a menu of 14 toppings if each topping can only be chosen once?
Answers
Rudy has 3003 different ways to choose 6 toppings from a menu of 14 toppings if each topping can only be chosen once.
The number of ways to choose 6 toppings from a menu of 14 toppings where each topping can only be chosen once is 14!/(14-6)! = 14!/(8!) = 3003. This is because for the first topping, Rudy has 14 options, for the second topping he has 13 options, for the third topping he has 12 options, and so on. To calculate the total number of combinations, we use the formula n!/(n-r)! where n is the number of items and r is the number of items to choose. This formula gives us the number of ways to choose r items from a set of n items without regard to order, which is the number of combinations.
The formula for combinations is given by n!/(n-r)! where n is the number of items and r is the number of items to choose. Here, n = 14 (the number of toppings on the menu) and r = 6 (the number of toppings Rudy wants to choose). So, the number of combinations is 14!/(14-6)! = 14!/(8!).
The factorial (!) is the product of all positive integers up to that number. For example, 4! = 4 x 3 x 2 x 1 = 24.
So, 14! = 14 x 13 x 12 x ... x 2 x 1 = 87178291199, and 8! = 8 x 7 x 6 x ... x 2 x 1 = 40320.
Now, to calculate the number of combinations, we divide 14! by 8!: 14!/(8!) = 87178291199/40320 = 3003.
Therefore, Rudy has 3003 different ways to choose 6 toppings from a menu of 14 toppings if each topping can only be chosen once.
To learn more about toppings please click on below link.
https://brainly.com/question/29858706
#SPJ4
If p and q vary inversely and p is 9 when q is 16, determine q when pis equal to 18.
Answers
Answer:
\(p \: \alpha \: \frac{1}{q} \\ p = \frac{k}{q} \\ k \: is \: a \: constant \: of \: proportionality \\ when \: p \: is \: 9.. \: \: q = 16 \\ 9 = \frac{k}{16} \\ k = 144 \\ when \: p \: is \: 18 : \\ 18 = \frac{144}{q} \\ q = \frac{144}{18} \\ q = 8\)
what is the distance formula
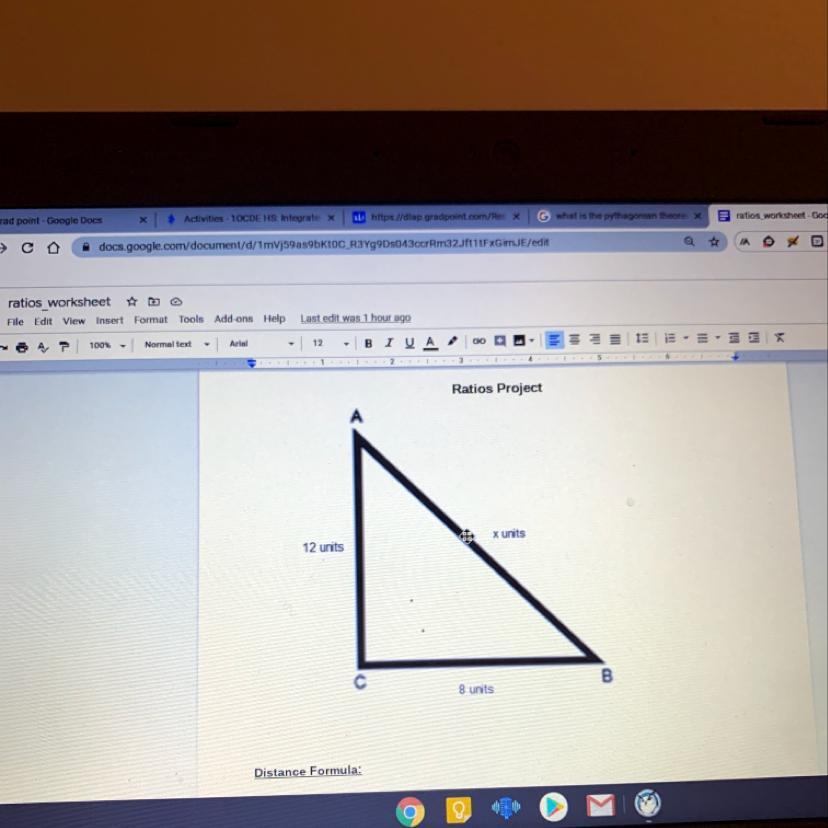
Answers
Answer:
14.42 units
Step-by-step explanation:
Assuming that this is a right triangle (i.e ∠ACB = 90°), we can use the Pythagorean formula to solve this:
AB² = AC² + BC²
AB² = 12² + 8²
AB = √(12² + 8²)
AB = 14.42 units

at a certain truck manufacturing plant, 8 trucks were produced last week. unknown to the manufacturer, 3 of the trucks had defective transmissions. suppose that a certain local shipping company has just purchased 2 trucks from the manufacturer. what is the probability that: a. both trucks purchased had defective transmissions? b. only one of the trucks had a defective transmission? c. suppose the company purchases 3 trucks. what is the probability that all 3 had defective transmissions?
Answers
The probability that both trucks purchased had defective transmissions is 9/64 and if one truck has then 30/56
Total trucks = 8
Trucks having defective transmissions = 3
Trucks purchased = 2
Let the event that a truck has a defective transmission be = D
Let the event that a truck does not have a defective transmission = ND
a. Probability that both trucks purchased had defective transmissions:
P(D) = number of defective trucks / total number of trucks
= 3/8
As the likelihood of the second truck being defective is unaffected by the first truck's defect, therefore,
P(D and D) = (3/8) x (3/8)
= 9/64
b. Probability that only one of the trucks had a defective transmission:
P(D) = 3/8
P(ND) = 1 - P(D)
1 - 3/8 = 5/8
Given that one of the trucks is already known to be defective, there is a 5/7 chance that the second truck will not be as well (since there are 5 non-defective trucks left out of 7 total remaining trucks). The likelihood that the second truck will be flawed in this instance is 3/7. (since there are 3 defective trucks left out of 7 total remaining trucks)
Therefore,
P(D and ND) + P(ND and D)
= (3/8) x (5/7) + (5/8) x (3/7)
= 15/56 + 15/56
= 30/56
c. Probability that all 3 trucks had defective transmissions:
Given that the first two trucks had problematic transmissions, there is a chance that the third truck will as well. The likelihood of the third truck being defective is 2/6 because it is already known that two of the trucks are problematic (since there are 2 defective trucks left out of 6 total remaining trucks)
Therefore,
P(D and D and D)
= (3/8) x (3/8) x (2/6)
= 9/128
Read more about probability on:
https://brainly.com/question/24756209
#SPJ4
If the sample data points are very close to the estimated regression line, then (Choose ALL the right answers.)
a. The slope will be a very big positive number.
b. It is likely to be a decreasing line.
c. The standard error is likely to be small.
d. The R square will tend to be high.
e. The line will look very ugly.
Answers
If the sample data points are very close to the estimated regression line, then standard error is likely to be small and R square will tend to be high. So, correct options are C and D.
Firstly, the slope of the regression line may not necessarily be a very big positive number. The slope of the line depends on the relationship between the independent and dependent variables, and how the dependent variable changes with a unit change in the independent variable.
If the data points are closely packed around the line, it means that the slope is more likely to be a moderate or small number.
Secondly, it is unlikely that the line will be decreasing, as the regression line is usually a straight line that shows the average relationship between the independent and dependent variables.
Thirdly, if the data points are very close to the estimated regression line, then the standard error is likely to be small. This means that the estimated regression line is a good fit for the data and the observed values are close to the predicted values.
Fourthly, the R square will tend to be high if the data points are close to the estimated regression line. R square is a measure of how well the regression line fits the data points, and if the data points are close to the line, then the R square will be higher.
Lastly, if the data points are very close to the estimated regression line, then the line is likely to look visually appealing and not "ugly." The regression line is a summary of the data and should be a good representation of the observed relationship between the variables.
So, correct options are C and D.
To learn more about regression click on,
https://brainly.com/question/29341200
#SPJ4
mark sweeney wants to receive a letter grade of a for this course, and he needs to earn at least 90 points to do so. based on the regression equation developed in part (b), what is the estimated minimum number of hours mark should study to receive a letter grade of a for this course? (round your answer to one decimal place.)
Answers
Mark needs to invest 5572.24 hours (rounded to one decimal place) of study time in order to achieve an A letter grade in this course.
To determine the estimated minimum number of hours Mark should study, we need to solve for the number of hours such that his predicted score, given by the regression equation from part (b), is at least 90.
The regression equation is as follows: Predicted score = 48.74 + 0.00726(number of hours studied)
Setting the predicted score equal to 90 and solving for the number of hours studied gives:90 = 48.74 + 0.00726 (number of hours studied)
Solving for the number of hours studied gives: number of hours studied = (90 - 48.74)/0.00726= 5572.24
Therefore, Mark should study for 5572.24 hours (rounded to one decimal place) to receive a letter grade of A for this course.
To know more about regression equation refer here:
https://brainly.com/question/30738733#
#SPJ11
Help!!! A teacher divided the class into two groups of equal size.
3 5 of the first group are right-handed.
80% of the second group are right-handed.
What fraction of the class is right-handed?
A.4/5
B.7/10
C.5/7
D.8/9
Answers
7/10 answer ///////////
Please help ASAP! Which ordered pair is a solution of this
equation?
-5x - 9y = -8
Click on the correct answer
A.
(2,-1)
B.
(-1,2)
C.
(-22)
D.
(2,-2)
Answers
========================================================
Explanation:
For each possible answer choice, you'll plug in the given coordinates to see which results in a true equation or not.
If we try choice A, then we plug in x = 2 and y = -1 to get
-5x-9y = -8
-5(2)-9(-1) = -8
-10+9 = -8
-1 = -8 which is false
So (x,y) = (2,-1) is not a solution. We can cross choice A off the list.
You'll find a similar situation happens with choices B and D. They don't work either.
-------
Choice C works because...
-5x-9y = -8
-5(-2)-9(2) = -8 .... replaced x with -2, replaced y with 2
10-18 = -8
-8 = -8
We get a true equation. So (-2,2) has been confirmed to be a solution.
A card from the set below is chosen at random.
What is the probability of drawing a card more than 6?
P (more than 6)

Answers
The probability of drawing a card that is more than 6 is given as 1 / 2.
How to find probabilityThe term probability can be defined as the concept in mathematics that has to do with the likelihood that an event is going to have to occur.
In the picture we have values that are numbered from 1 to 12 in the face of all of the cards.
The cards that are greater than 6 here are: [7, 8, 8, 10, 11, 12] = 6
The total numbers in the card are: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12] = 12
Hence the probability of card that is more than 6 = 6 / 12
= 1/2
Read more on probability here: https://brainly.com/question/24756209
#SPJ1
How do you find the third side of an inequality of a triangle?
Answers
To find the third side of an inequality of a triangle, you must first use the Triangle Inequality Theorem.
This theorem states that for any triangle, the sum of any two sides of the triangle must be greater than the third side. This means that in order to find the length of the third side, you must subtract the sum of the two known sides from the smaller of the two sides, then the length of the third side will be equal to the difference between these two numbers. For example, if two sides of a triangle have lengths of 4 and 3, the third side must be greater than 1 (4 + 3 = 7 and 4 - 3 = 1). Therefore, the length of the third side must be greater than 1.
Learn more about Triangle Inequality Theorem here:
https://brainly.com/question/1163433
#SPJ4
The table represents some points on the graph of a linear function.
х
-7.5
-3.5
-1
2
3.5
у
12
0
-7.5
-16.5
-21
Which function represents the same relationship?
Answers
Answer:
y=-3x-10.5
Step-by-step explanation:
Let's use the first set of numbers.
-7.5 and 12
-3.5 and 0
Our rise here is -12 and run is 4. So, our slope is -3.
Now we just need our intercept.
y = mx + b
y = -3x + b
0 = -3(3.5) + b
b = -10.5
The function represents the same relationship between x and y will be x + 3y + 3.5 = 0.
What is the equation of a line passing through two points?Let the equation of the line pass through (x₁, y₁) and (x₂, y₂). Then the equation of the line is given as,
\(\rm (y - y_2) = \left (\dfrac{y_2 - y_1}{x_2 - x_1} \right ) (x - x_2)\)
The table represents some points on the graph of a linear function.
х у
-7.5 12
-3.5 0
-1 -7.5
2 -16.5
3.5 -21
Take two points from the table, then the points are (-7.5, 12) and (-3.5, 0). Then the equation of the line is given as,
y - 0 = [(-3.5 + 7.5) / (0 - 12)](x + 3.5)
y = - (1/3)(x + 3.5)
3y = - x - 3.5
x + 3y + 3.5 = 0
The function represents the same relationship between x and y will be x + 3y + 3.5 = 0.
More about the line passing through two points link is given below.
https://brainly.com/question/12740817
#SPJ5
If cot= -1/3 and cos theta Greater than 0, find the trigonometric function values in simplest radical form
Answers
Answer:
Step-by-step explanation:
If cot= -1/3 and cos theta Greater than 0, find the trigonometric function values in simplest radical form
Which quadratic function in vertex form can be represented by the graph that has a vertex at (3, -7) and passes through the point (1, -10)?
I really need the answer QUICK please

Answers
Answer:
Answer is D
Step-by-step explanation:
(3,-7) and (1,-10) belong toD Variant
The required function is \(y=-\frac{3}{4}(x-3)^2-7\) , so the correct option is D.
Important information:
Vertex = (3,-7)Other point = (1,-10)Quadratic function:The vertex form of a quadratic function is:
\(y=a(x-h)^2+k\)
Where, \(a\) is constant and \((h,k)\) is vertex.
Substitute \(h=3,k=-7\).
\(y=a(x-3)^2-7\) ...(i)
Graph passes through the point (1, -10). Substitute \(x=1,y=-10\) in (i).
\(-10=a(1-3)^2-7\)
\(-10+7=4a\)
\(-3=4a\)
\(\dfrac{-3}{4}=a\)
Substitute \(a=-\dfrac{3}{4}\) in (i).
\(y=-\frac{3}{4}(x-3)^2-7\)
Therefore, the correct option is D.
Find out more about 'Quadratic function' here:
https://brainly.com/question/15280010