1) Sally spent half of her allowance going to the movies. She washed the family
car and earned eight dollars. What is her weekly allowance if she ended with
twelve dollars ?
Thinking it has to be at least a multi-step equation and possibly show steps
Answers
Answer:
$4
Step-by-step explanation:
If she had earned $8 washing a car and had at the end $12 you would calculate:
12-8=4
Related Questions
Please help me as fast as possible!
A tortoise and hare decide to race 30 feet. The hare, being much faster, decides to give
the tortoise a 20 feet head start. The tortoise runs at 0.5 feet/sec and the hare runs at
5.5 feet/second. How long (in seconds) until the hare catches the tortoise?
Answers
4 seconds
Explanation:
If they’re going to meet at a certain point, the hate and the tortoise would have raced the same distance up until that point. So we can lay the equation like this:
The distance the tortoise crawled=the distance the hare hopped
Another important formula that we must know to solve this equation is:
Distance=time*speed
Because what we don’t know and want to solve for is the TIME, we can set our variable as t.
The equation now:
[tortoise speed]*t+20ft=[hare speed)*t
We add 20ft on the left because the hare gave the tortoise a head start.
When we input all the values, the final equation is:
0.5t+20=5.5t
The process of solving it is in the picture below.
I hope this helped (at least a little haha, this is a pretty confusing question)

URGENT:
Solve this literal equation!
ax + b = c for a
Answers
Answer:
A=\(\frac{C-B}{X}\)
Step-by-step explanation:
Subtract both sides with B
AX=C-B
Divide both sides by X to get A alone.
A=\(\frac{C-B}{X}\)
What is the measure of AngleDCF?
Three lines extend from point C. The space between line C D and C E is 75 degrees. The space between lines C E and C F is 54 degrees.
The measure of AngleDCF is
degrees.
Answers
Answer:
129°
Step-by-step explanation:
∠DCE = 75
∠ECF = 54
∠DCF = ∠DCE + ∠ECF
= 75 + 54
= 129°
Answer:
129
Step-by-step explanation:
what comes next
8,28,48,_,_,_
Answers
Which of the correlation values represent a perfect linear relationship between x and y?
a. 0.5
b. 1
c. 100
d. -1
e. 0
Answers
The correlation values 1 and -1 represent a perfect linear relationship between the two variables x and y.
Step to Step explanation:
To represent perfect linear relationship between two variables the correlation values should be 1 and -1.When correlation value is equal to 1 it represent the positive linear relationship between two variables x and y.Slope of the correlation value positive 1 indicates the increasing slope.When correlation value is equal to -1 it represent the negative linear relationship between two variables x and y.Slope of the correlation value negative 1 indicates the decreasing slope.Therefore, the perfect linear relationship between two variables x and y is given correlation value 1 and -1.
Learn more about correlation value here
brainly.com/question/14916932
#SPJ4
Find the surface area of a chalk box whose length, breadth and height are 16 cm, 8 cm , 6 cm respectively?
Answers
The surface area of the chalk box is 544 square centimeters.To find the surface area of a rectangular prism (chalk box), we need to calculate the sum of the areas of its six faces.
The formula for the surface area of a rectangular prism is:
Surface Area = 2(length × breadth) + 2(breadth × height) + 2(length × height)
Given the dimensions of the chalk box:
Length = 16 cm
Breadth = 8 cm
Height = 6 cm
Substituting these values into the formula:
Surface Area = 2(16 cm × 8 cm) + 2(8 cm × 6 cm) + 2(16 cm × 6 cm)
Surface Area = 2(128 cm²) + 2(48 cm²) + 2(96 cm²)
Surface Area = 256 cm² + 96 cm² + 192 cm²
Surface Area = 544 cm²
Therefore, the surface area of the chalk box is 544 square centimeters.
To learn more about length click here:
brainly.com/question/28983035
#SPJ11
Find the missing number
9, 12, 15, ____, 21
4, 8, 12, ____, 20
60, 55, 50, ____, 40
42, 52, 62, _____, 82
17, 22, 27, _____, 37
50, 48, 46, 44, ____
12, 14, 16, 18, ____
25, 21, 17, 13, ____
96, 90, 84, ____, 72
64, 32, 16, 8, ____
Answers
4, 8, 12, 16, 20
60, 55, 50, 45, 40
42, 52, 62, 72, 82
17, 22, 27, 32, 37
50, 48, 46, 44, 42
12, 14, 16, 18, 20
25, 21, 17, 13, 9
96, 90, 84, 78, 72
64, 32, 16, 8, 4
Answer:
1. 18
2. 16
3. 45
4. 72
5. 32
6. 42
7. 20
8. 9
9. 78
10. 4
Eliminate arbitrary constants. Y=c1x+c2x^2+sinx
Answers
Step-by-step explanation:
chicken
Find S? Please help, thank you :)
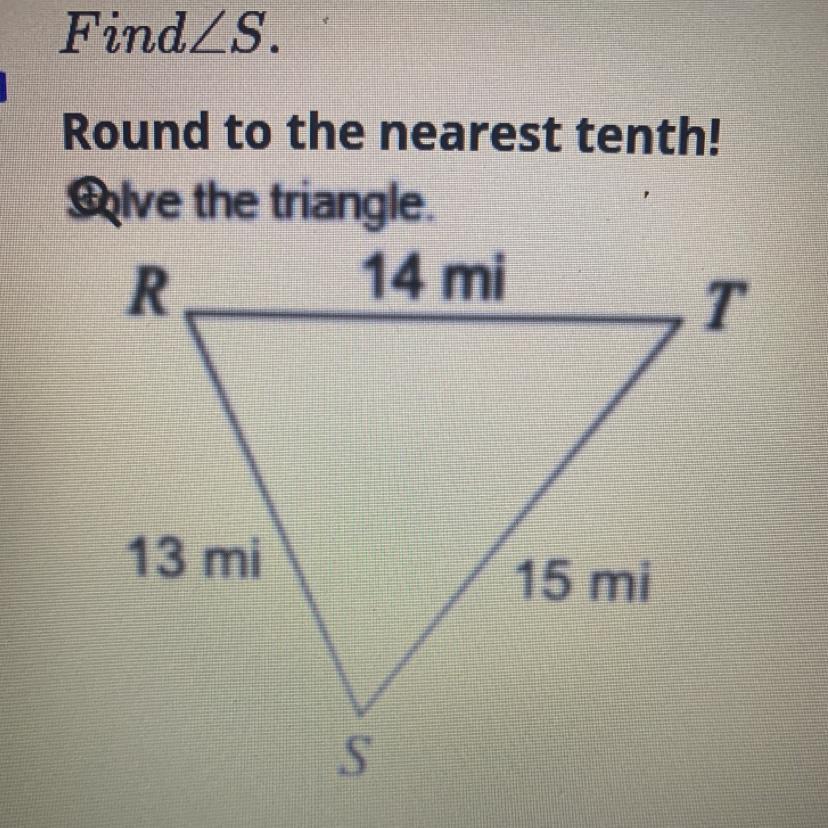
Answers
Answer:
If I am correct, the answer should be 70.1 degrees.
3 − 3k + 7k = 5b\(3 − 3k + 7k = 5b\)
Answers
Answer:
k=-14
Step-by-step explanation:
Mr kuldeep bought 7½ kg of and Mr Rajesh bought 5¾ kg of rice .who bought more rice and by how much.
Answers
Mr. Kuldeep bought more rice than Mr. Rajesh by 1¾ kg, or 1.75 kg more than Mr. Rajesh.
Mr. Kuldeep bought 7½ kg of rice and Mr. Rajesh bought 5¾ kg of rice. To find out who bought more rice and by how much, we need to compare the two quantities.
First, let's convert the mixed numbers into improper fractions:
7½ kg = (7 x 2 + 1)/2 = 15/2 kg
5¾ kg = (5 x 4 + 3)/4 = 23/4 kg
Now, let's compare the two fractions:
15/2 kg > 23/4 kg
Therefore, Mr. Kuldeep bought more rice than Mr. Rajesh.
To find out by how much, we need to subtract the smaller quantity from the larger one:
15/2 kg - 23/4 kg = (30 - 23)/4 kg = 7/4 kg
So, Mr. Kuldeep bought 7/4 kg or 1¾ kg more rice than Mr. Rajesh. In conclusion, Mr. Kuldeep bought more rice than Mr. Rajesh by 1¾ kg.
Here to learn more about Fractions at the link https://brainly.com/question/78672
#SPJ11
Need A B C and domain and the range.

Answers
Answer:
A=1 B=2 C=3 Domain: [2, infinity) Range: (neg. infinity, 3]
Step-by-step explanation:
a is rate B is Horitzontal shift C is vertical shift
b=2
c=3
a is the rate of B is horizontal to C is vertical shift
Simplify the following:
(4x2+ 7x + 8) - (-3x3 + 5x + 2)
What did you do to get this answer
Answers
Answer:
beuwhwvd
Step-by-step explanation:
Question 3- Please help. Find the area of the sector for the image below:

Answers
Answer:
The answer is 16.8 cm^ 2.
PLEASE HELP!! Will give brainlist to correct answer!! :)
What is the solution to the equation? 21/−4h=14/11+h Enter your answer in the box
Answers
The solution to the equation 21/−4h=14/11+h is -3.
To solve the equation, follow this method.
1: Cross-multiplication eliminate the denominators in the given equation, we cross-multiply the terms on either side of the equation. This can be represented as follows:
11 + h = (14 x -4h)/21
2: We multiply 14 with -4h which is equivalent to -56h. Hence, the equation can be rewritten as follows:
11 + h = -56h/21
3: Multiply by the LCM of denominators.To eliminate the fraction on the right-hand side, we multiply both sides of the equation by the LCM of the denominators. Here, the LCM of denominators 21 and 1 is 21. Hence, we can rewrite the equation as follows:
21(11 + h) = -56h
4: Now, we simplify the equation by distributing 21 over the brackets. This can be represented as follows:
231 + 21h = -56h
Now, we move the variable terms to the left-hand side of the equation and the constant terms to the right-hand side of the equation. This can be represented as follows:
77h = -231h = -231/77 = -3
Therefore, the solution to the given equation is h = -3.
You can learn more about cross-multiplication at: brainly.com/question/27812904
#SPJ11
11 Finding a difference quotient for a linear or quadratic function V Find the difference quotient f(x)=-3x²-2x+5 Simplify your answer as much as possible. f(x +h)-f(x) h f(x+h)-f(x) h = ( where h#0,
Answers
The difference quotient for the given function is 9 -2/h.
The difference quotient for the given function can be calculated as:
[f(x+h) - f(x)]/h
= [(3(x+h)² - 2(x+h) + 5) - (3x² - 2x + 5)]/h
= (3x² + 6xh + 3h² - 2x - 2h + 5 - 3x² + 2x - 5)/h
= (6xh + 3h² - 2h)/h
= (6x + 3h -2)/h
Simplifying the expression further, we get:
(6x + 3h -2)/h = 6 + 3h/h -2/h
= 6 + 3 -2/h
= 9-2/h
Therefore, the difference quotient for the given function is 9 -2/h.
Learn more about the quadratic function here:
https://brainly.com/question/29775037.
#SPJ4
"Your question is incomplete, probably the complete question/missing part is:"
Find the difference quotient [f(x+h)-f(x)]/h, where h≠0, for the function below.
f(x)=3x² -2x+5. Simplify your answer as much as possible.
dx dy = x - y², = y - x² dt dt (a) Determine all critical points of the given system of equations. (b) Find the corresponding linear system near each critical point. (c) Find the eigenvalues of each linear system. What conclusions can you then draw about the nonlinear system? (d) Draw a phase portrait of the nonlinear system to confirm your conclusions.
Answers
The critical points are (0, 0) and (1, 1).
Near (1, 1), linear system becomes
\($\frac{d}{dt} \begin{bmatrix}x \\ y\end{bmatrix} = \begin{bmatrix}-1 & -2 \\ 1 & 0\end{bmatrix} \begin{bmatrix}x \\ y\end{bmatrix}$\)
Eigenvalues are complex and not real.
(0, 0) is a stable equilibrium point and (1, 1) is an unstable equilibrium point.
From the phase portrait, we can conclude that (0, 0) is a stable equilibrium point and (1, 1) is an unstable equilibrium point.
(a) Critical points are the points where dx/dt = 0 and
dy/dt = 0.
So, we need to solve the following equations:
x - y² = 0 and
y - x² = 0
Solving them, we get (0, 0) and (1, 1) as critical points.
(b) Linear system near (0, 0):
Near (0, 0), linear system becomes
\($\frac{d}{dt} \begin{bmatrix}x \\ y\end{bmatrix} = \begin{bmatrix}0 & -2 \\ 1 & 0\end{bmatrix} \begin{bmatrix}x \\ y\end{bmatrix}$\)
Linear system near (1, 1): Near (1, 1), linear system becomes
\($\frac{d}{dt} \begin{bmatrix}x \\ y\end{bmatrix} = \begin{bmatrix}-1 & -2 \\ 1 & 0\end{bmatrix} \begin{bmatrix}x \\ y\end{bmatrix}$\)
(c) Eigenvalues of the linear system near (0, 0):
\($\begin{vmatrix}0 - \lambda & -2 \\ 1 & 0 - \lambda\end{vmatrix} = 0$\)
λ² + 2 = 0
Eigenvalues are ±√2i.
Eigenvalues of the linear system near (1, 1):
\($\begin{vmatrix}-1 - \lambda & -2 \\ 1 & 0 - \lambda\end{vmatrix} = 0$\)
λ² + λ + 2 = 0
Eigenvalues are complex and not real.
(d) The phase portrait of the nonlinear system is as follows:
As we can see from the phase portrait, at the critical point (0, 0), the eigenvalues of the linear system are purely imaginary, which means the origin is a center.
At the critical point (1, 1), the eigenvalues of the linear system have non-zero real parts, which means the critical point is unstable.
So, from the phase portrait, we can conclude that (0, 0) is a stable equilibrium point and (1, 1) is an unstable equilibrium point.
To know more about equations visit
https://brainly.com/question/17145398
#SPJ11
At an elite baseball camp, 60% of players can bat both right-handed and left-handed. If 25% of the players who bat left-handed do not bat right-handed, what is the probability that a player selected at random does not bat left-handed?
Answers
Answer:
The probability that a player selected at random does not bat left-handed is 20%.
Step-by-step explanation:
Assume that there are a total of 100 baseball players at an elite baseball camp.
The information provided is:
60% of players can bat both right-handed and left-handed. 25% of the players who bat left-handed do not bat right-handed.That is, the number of players can bat both right-handed and left-handed is,
n (L and R) = 60.
Now, if 25% of the players who bat left-handed do not bat right-handed, then 75% of all left-handed players can also bat right-handed.
⇒ n (L and R) = n (L) × 75%
60 = n (L) × 0.75
n (L) = 60/0.75
n (L) = 80
So there are 80 left handed batters.
Compute the number of only left handed batters as follows:
n (Only L) = n (L) × 25%
= 80 × 0.25
= 20
So there are 20 only left handed batters.
Compute the number of only right handed batters as follows:
Total = n (Only L) + n (Only R) + n (L and R)
100 = 20 + n (Only R) + 60
n (Only R) = 20
Thus, the probability that a player selected at random does not bat left-handed is 20%.
consider the surface with parametric equations r(s,t)=⟨st,s+t,s−t⟩r(s,t)=⟨st,s+t,s−t⟩.
Answers
The surface you provided has parametric equations given by: r(s, t) = ⟨st, s + t, s - t⟩ The vector r(s, t) represents the position of a point on the surface in terms of two parameters, s and t. As s and t vary, different points on the surface are defined, creating the 3D shape of the surface.
This surface is defined by the parametric equations r(s,t)=⟨st,s+t,s−t⟩, which means that for every combination of s and t, we can get a point on the surface. The three components of the vector r(s,t) give the coordinates of that point in 3D space.
One interesting thing about this surface is that it's defined by a set of parametric equations that are themselves parametric. That is, the equations for r(s,t) include the parameters s and t, which are themselves variables that can take on any value.
Another interesting thing is that this surface is defined by a set of equations that are parametric, but not necessarily in terms of time. In other words, these equations don't necessarily describe the motion of an object through time, but rather describe the relationship between two variables (s and t) that define the surface.
In terms of its shape, the surface defined by r(s,t) has a parabolic profile that opens up in the s and t directions. This means that as s and t increase, the surface curves upward and outward, forming a bowl-like shape.
Overall, this is an example of a parametric surface that can be defined by a set of equations that are themselves parametric. While it may not have any real-world applications, it's an interesting mathematical construct that helps us understand how parametric equations can be used to describe complex shapes in 3D space.
To know more about parabolic visit:
https://brainly.com/question/30345364
#SPJ11
Mrs Llanes ordered 4 pizzas for her class they ate5/6 of the pizza how much did they eat?
Answers
Answer:
Here you go
Step-by-step explanation:
\(\frac{4}{1} *\frac{5}{6} = \frac{20}{6} = 3 \frac{2}{6} = 3\frac{1}{3} \\\\They~ ate ~3 ~and ~\frac{1}{3} ~of ~the ~ pizza\)
A meal costs $5.75. You offer a 10% discount. The sales tax is 4%. How much should you charge the customer? $
Answers
Answer:
To calculate the final cost of the meal, we need to first calculate the discount and then add the sales tax. Discount = 10% of $5.75 = $0.575 Price after discount = $5.75 - $0.575 = $5.175 Sales tax = 4% of $5.175 = $0.207 Final cost = Price after discount + Sales tax = $5.175 + $0.207 = $5.382 Therefore, you should charge the customer $5.382.
well, let's hmmm apply the 10% discount first
\(\begin{array}{|c|ll} \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{10\% of 5.75}}{\left( \cfrac{10}{100} \right)5.75} ~~ \approx ~~ 0.58~\hfill \stackrel{ 5.75~~ - ~~0.58 }{\approx\text{\LARGE 5.17}}\)
now let's apply the 4% tax to it
\(\stackrel{\textit{4\% of 5.17}}{\left( \cfrac{4}{100} \right)5.17} ~~ \approx ~~ 0.21\hspace{5em}\stackrel{ 5.17~~ + ~~0.21 }{\text{\LARGE 5.38}}\qquad \textit{final charge}\)
I need help doing a two column proof for this please

Answers
The congruent arcs arcAB and arcCD, indicates that the chords AB and CD are also congruent, which indicates that quadrilateral ABCD is an isosceles trapezium and ∠A = ∠C
What is an isosceles trapezoid?An isosceles trapezoid is a trapezoid that has congruent base angles and congruent non parallel sides.
The quadrilateral ABCD is a trapezoid, therefore;
BD is parallel to AC
The measure of the arcs AB and CD are the same;
arcAB = arcCD
The converse of the chord and intercepted arc theorem indicates that the lengths of the chords, AB and CD are the same, therefore;
The trapezoid ABCD is an isosceles trapezoid
Which indicates that the base angles ∠A and ∠C are congruent
∠A ≅ ∠C
Therefore; ∠A = ∠C
Learn more on theorems with regards to chords in a circle here: https://brainly.com/question/13388199
#SPJ1
arron ran a distance of 5km at an average speed of 2.2m/s
how long did aaron run for
give your answer in minutes and seconds to the nearest second
Answers
The number of minutes Arron taken to run is 38 minutes.
Given that, Arron ran a distance of 5 km at an average speed of 2.2 m/s.
What is the speed?The speed formula can be defined as the rate at which an object covers some distance. Speed can be measured as the distance travelled by a body in a given period of time. The SI unit of speed is m/s.
Here, 5 km=5000 m
We know that, speed = Distance/Time
2.2 = 5000/Time
⇒ Time =5000/2.2
⇒ Time = 2272.73 sec
Number minutes =2272.73/60
= 37.87
≈ 38 minutes
Therefore, the number of minutes Arron taken to run is 38 minutes.
To learn more about the speed, distance, and time visit:
brainly.com/question/4978052.
#SPJ1
Gina competed in a gymnastics competition. Her total score for the balance beam and the vault was 16.75. She scored 9.3 on the vault. How much did she score for the balance beam?
Answers
To calculate how much dod
what is the inverse of the function y=5x+30?
Answers
The inverse of the function is y = ( 1/5 )x - 6.
An expression, rule, or law in mathematics that establishes the relationship between an independent variable and a dependent variable. In mathematics, functions exist everywhere, and they are crucial for constructing physical links in the sciences.
Consider the function,
y = 5x + 30
To find the inverse of the function we interchange x and y then find the equation for y.
Therefore, after interchanging x and y:
x = 5y + 30
Subtracting 30 from each side of the equation.
x - 30 = 5y + 30 - 30
x - 30 = 5y
Now, dividing the whole equation by 5
( x - 30 ) / 5 = 5y / 5
y = ( 1/5 )x - 30/ 5
y = ( 1/5 )x - 6
Therefore, the inverse of the function y = 5x + 30 is y = ( 1/5 )x - 6.
Learn more about inverse here:
https://brainly.com/question/3831584
#SPJ9
What is the equation for the line that has a slope of -1/2 and a y-intercept at (0,6)?
Answers
Answer:
y=-1/2+6
Step-by-step explanation:
Answer:
Y= -1/2x + 6
Step-by-step explanation:
A jet travels 490 miles in 5 hours. At this rate, how far could the jet fly in 12 hours? What is the rate of speed of the jet?
Answers
Answer: 1,176 miles
Step-by-step explanation:
490 / 5 = 98 miles
98 mph X 12 hours is 1,176
Question 22 of 25
What is the value of y in the parallelogram below?
D
с
3y
78°
A
B
A. 26
B. 75
O
C. 99
D. 34

Answers
Answer:
Option DThe value of y in the parallelogram is 34°
Step-by-step explanation:
Adjacent angles of the Parallelogram are supplementary
So,
(78° + 3y°) = 180°
78° + 3y° = 180°
Subtract 78° each side we get,
78° - 78° + 3y° = 180° - 78°
3y° = 102°
Now, Divide both side by 3 we get,
3y°/3 = 102°/3
y = 34°
Thus, The value of y in the parallelogram is 34°
-TheUnknownScientist 72
Someone help me with this pls

Answers
Answer:
C
Step-by-step explanation:
\((a^{-2}*8^{7})^2 = a^{-2*2}*8^{7*2} = a^{-4}*8^{14}\)
• Number of Combinations: (K) = k!(n-k)! 1. (30p) Consider the following equation: x1 + x2 + x3 + x4 + x5 = 20 where x₁, i = 1, ..., 5 are positive integers. How many distinct assignments can be made to the vector (x1, x2, x3, x4, x5)' satisfying the above equation?
Answers
There are 10,626 distinct assignments that can be made to the vector (x₁, x₂, x₃, x₄, x₅)' satisfying the given equation.
The given equation is x₁ + x₂ + x₃ + x₄ + x₅ = 20, where x₁, x₂, x₃, x₄, x₅ are positive integers.
We can solve this problem using the concept of stars and bars. Imagine we have 20 stars representing the total value of 20, and we want to distribute these stars among the 5 variables x₁, x₂, x₃, x₄, and x₅. The bars act as separators to divide the stars into different groups representing the values of each variable.
For example, if we have the arrangement "* | * * * | * * * * * | * * * | *", it represents x₁ = 1, x₂ = 3, x₃ = 5, x₄ = 3, and x₅ = 1.
To determine the number of distinct assignments, we need to find the number of ways we can place the bars among the stars. Since we have 4 bars and 20 stars, the total number of distinct assignments is given by the number of combinations of choosing 4 positions out of 24 (20 stars + 4 bars). This can be calculated using the formula for combinations:
C(n, k) = n! / (k!(n-k)!)
Applying this formula, the number of distinct assignments is:
K = C(24, 4) = 24! / (4!(24-4)!) = 10,626
Therefore, there are 10,626 distinct assignments that can be made to the vector (x₁, x₂, x₃, x₄, x₅)' satisfying the given equation.
Learn more about vectors here: brainly.com/question/24256726
#SPJ11