1. Nina had Marbles. She gave 15 to Jane and 16 to Cherry. Louie arrived and got 12 from Nina. If Nina has 22 left, how many marbles did she have at first?
Answers
Answer
Explanation
Given the word problem, we can deduce the following information:
Jane = 15 marbles
Cherry=16 marbles
Louie = 12 marbles
Nina = 22 marbles left
To determine the total number of marbles Nina have at first, we add the number of marbles as shown below:
\(\begin{gathered} Total=15+16+12+22 \\ Calculate \\ Total=65 \end{gathered}\)Therefore, the answer is 65 marbles.
Related Questions
From the top of a lighthouse 82 m tall, a guard sees two ships at sea.
The angle of depression to the closer ship is 53° and to the further ship is 39°.
How far are the ships apart from each other to the nearest metre?

Answers
The distance between the two ship based on the angle of depression is 42 meters.
The distance of each ship can be calculated thus:
TanX = opposite / Adjacent
The first ship:
Tan53 = distance/ 82
distance= 108.82 meters
The second ship:
Tan39 = distance/ 82
distance= 66.40 meters
The Difference between the ships are :
108.82 - 66.40 = 42.42 metersTherefore, the distance between the two ships is 42 meters.
Learn more on angles of depression:https://brainly.com/question/17193804
#SPJ1
Every Morning, Julio drives his 1.5 hour route to gather the children for school. His route covers 45 miles and there are 60 kids on the route. Create a tape diagram to determine how many miles are traveled in one hour
Answers
I provided tape diagram in attachment

The amount of money in the account after 18 years will be $449.5.
What is tape diagram?A tape diagram is a pictorial model students can draw to represent a mathematical relationship or to develop understanding of a math concept. Tape diagrams are useful for solving many different types of math problems but are commonly used with word problems.Given is that every Morning, Julio drives his 1.5 hour route to gather the children for school. His route covers 45 miles and there are 60 kids on the route.
Refer to the tape diagram given. It shows that in one hour, a total of 30 miles have been covered.
Therefore, the amount of money in the account after 18 years will be $449.5.
To solve more questions on tape diagram, visit the link below -
https://brainly.com/question/813658
#SPJ2

a coffee company wants to estimate the true proportion of the u.s. population that drinks its brand. it interviewed randomly selected people, and responded that they drink the company's brand. construct a percent confidence interval for the true proportion of people who drink the company's brand. group of answer choices
a) Construct a 95 percent confidence interval for the true proportion of people who drink the company’s brand.
b) How many individuals should be surveyed to be 95 percent confident of having the true proportion of people drinking the brand estimated to within 0.015?
Answers
You have a 5% chance of being wrong with a 95% confidence interval. With a 90 percent certainty span, you have a 10 percent chance of being incorrectly.
A confidence interval of ninety-nine percent would be larger than a confidence interval of ninety-five percent (for instance, plus or minus 4.5 percent as opposed to 3.5 percent).
We now have: 32 125 0.256 1 At a confidence level of 95 percent:
Zenit = 20.05/2 = 2196 95 percent confidence interval:
Considering the estimated proportion (P) = 0.256 n = = Zverit PL1-P) E 1.96 12 0.015) 0.256 (1-0.256) = 3251.94 3252
Zerit = 20.05/2 = 1.96 At 95%
confidence lovel margin of error (E) = 0.015
Now P = zerit / PL1-£) = 0.256 1.96 X 0.2561-0.256 125 = 0.256 0.0765.
To learn more about confidence interval here:
https://brainly.com/question/24131141
#SPJ4
what is the equation in slope- intercept form of the line that passes through the points (-26 -11) and (39, 34) ?A) y = -9/13 x + 7 B) y = -9/13 x - 7 C) y = 9/13 x + 7 D) y = 9/13 x - 7
Answers
what is the equation in slope- intercept form of the line that passes through the points (-26 -11) and (39, 34) ?
A) y = -9/13 x + 7
B) y = -9/13 x - 7
C) y = 9/13 x + 7
D) y = 9/13 x - 7
step 1
Find out the slope
m=(34+11)/(39+26)
m=45/65
simplify
m=9/13
step 2
Find the equation in slope intercept form
y=mx+b
we have
m=9/13
point (39,34)
substitute and solve for b
34=(9/13)(39)+b
b=34-27
b=7
therefore
the equation is
y=(9/13)x+7
option C1) 100×blank-100=100
2)(200-blank)×200=200
Answers
100x2=200-100=100
2. 200-199x200=200
200-199=1x200=200
*PRE-CALC URGENT + 100 POINTS*
A jumping spider's movement is modeled by a parabola. The spider makes a single
jump from the origin and reaches a maximum height of 20 mm halfway across a horizontal distance of 160 mm.
Part A: Write the equation of the parabola in standard form that models the spider's jump. Show your work. (4 points)
Part B: Identify the focus, directrix, and axis of symmetry of the parabola. (6 points)
Answers
Answer:
A. (x - 80)² = -320(y = 20)
B. Focus: (80, -60)
Directrix: y = 100
Axis of symmetry: x = 80
Step-by-step explanation:
Part AIf the spider's movement is modeled by a parabola, and its maximum height is 20 mm halfway across a horizontal distance of 160 mm, then:
x-intercepts = (0, 0) and (160, 0)Vertex = (80, 20)Standard form of a parabola with a vertical axis of symmetry:
\(\boxed{(x-h)^2=4p(y-k) \quad \textsf{where}\:p\neq 0}\)
If p > 0, the parabola opens upwards, and if p < 0, the parabola opens downwards.
\(\textsf{Vertex}=(h, k)\)\(\textsf{Focus}=(h,k+p)\)\(\textsf{Directrix}:y=(k-p)\)\(\textsf{Axis of symmetry}:x=h\)Substitute one of the x-intercepts and the vertex into the formula and solve for p:
\(\implies (0-80)^2=4p(0-20)\)
\(\implies (-80)^2=4p(-20)\)
\(\implies 6400=-80p\)
\(\implies p=-80\)
Substitute the found value of p and the vertex into the formula to create the equation of the parabola in standard form:
\(\implies (x-80)^2=4(-80)(y-20)\)
\(\implies (x-80)^2=-320(y-20)\)
Part BGiven:
h = 80k = 20p = -80\(\begin{aligned}\textsf{Focus}&=(h,k+p)\\&=(80,20-80)\\&=(80,-60)\end{aligned}\)
\(\begin{aligned}\textsf{Directrix}:y&=(k-p)\\ \implies y&=(20-(-80))\\ \implies y&=100\end{aligned}\)
\(\begin{aligned}\textsf{Axis of symmetry}:x&=h\\ \implies x&=80\end{aligned}\)

What is the range of the relation {(-10, 0), (10, 6), (0, 1), (5, 11), (8,3)}?
Answers
Using it's concept, the range of the relation is given by:
{0, 1, 3, 6, 11}.
What is the range of a relation?The range of a relation is the set that contains all output values of the relation, that is, all values of y.
The points given are in the (x,y) format, hence the range of the relation is given by:
{0, 1, 3, 6, 11}.
More can be learned about the range of a function at https://brainly.com/question/10891721
#SPJ1
I went to the store and bought 4 packs of nerds for $0.98 each and a pack of Little Debbie cakes for $2.15. How
much money did I spend?
Answers
Answer:
Kindly refer to the attachment
Thank U Next
I'll Give brainliest to whoever answers is correct
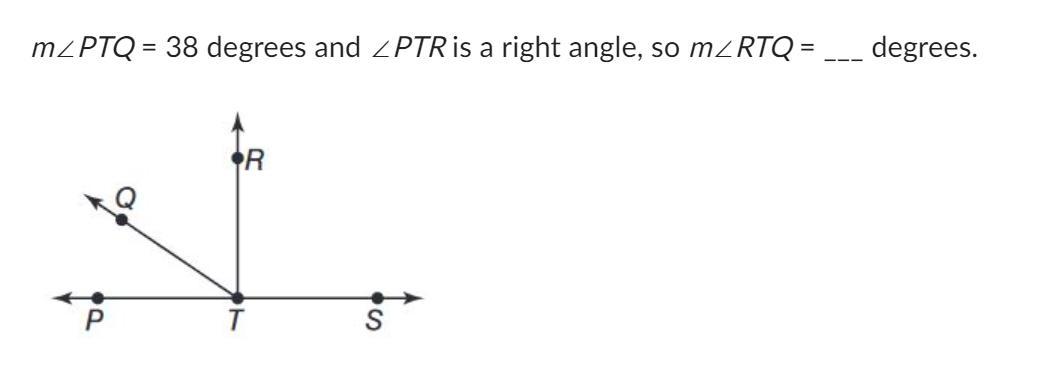
Answers
Answer:
52
Step-by-step explanation:
RTQ is 52 because if PTR is a right angle, right angles equal 90 degrees. So if PTQ is 38 degrees, we subtract 38 from 90 to get RTQ. 90-38 equals 52.
Answer:
52 degrees
Step-by-step explanation:
right angle = 90
90-38=52
So RTQ = 52 degrees
If a driver uses of a tank of gas every day, what fraction of a tank will he use in a) 3 days? b) 1 week?
Answers
Answer:
Step-by-step explanation:
a) If a driver uses a full tank of gas every day, the fraction of a tank he will use in 3 days is 3/1, or 3/1 of a tank.
b) If a driver uses a full tank of gas every day, the fraction of a tank he will use in 1 week is 7/1, or 7/1 of a tank.
It's worth noting that tanks of gas come in different sizes, so the amount of gas consumed in a day, week, or any other period of time will depend on the size of the tank, and the consumption of the car, so this answer is based on the assumption that a full tank is used every day.
Claude has a 10-pound package of hamburger meat and an
11.5-pound package of hamburger meat. Can he make the number of
hamburger patties shown? Choose Yes or No.
A. 87 1/4-pound hamburger patties
B. 45 1/2-pound hamburger patties
C. 30 1/2 -pound and 274-pound hamburger patties
D. 29 3/4 -pound hamburger patties
Answers
Answer: We can solve this problem by finding the total weight of the meat and then dividing by the weight of each patty to see if we can make the desired number of patties.
Let's add the weights of the two packages of meat:
10 + 11.5 = 21.5
For option A, we need 87 1/4-pound patties.
Each pound of meat will yield 4 patties of this size, so 21.5 pounds of meat will yield:
21.5 x 4 = 86 patties
Since we need 87 patties, Claude does not have enough meat for option A.
For option B, we need 45 1/2-pound patties.
Each pound of meat will yield 2 patties of this size, so 21.5 pounds of meat will yield:
21.5 x 2 = 43 patties
Since we need 45 patties, Claude does not have enough meat for option B.
For option C, we need 30 1/2-pound patties and 2 74-pound patties.
Each pound of meat will yield 2 patties of the smaller size and 1 patty of the larger size, so 21.5 pounds of meat will yield:
(21.5 x 2) + (2 x 1) = 43 + 2 = 45 patties
Since Claude only has 21.5 pounds of meat, he does not have enough for option C.
For option D, we need 29 3/4-pound patties.
Each pound of meat will yield 1.5 patties of this size, so 21.5 pounds of meat will yield:
21.5 x 1.5 = 32.25 patties
Since we only need 29.75 patties, Claude has enough meat for option D.
Therefore, the answer is Yes, Claude can make 29 3/4-pound hamburger patties.
Solve the equation. -z/4 = -3/4
Answers
answer
-z•1=-3-1
z=-3•-1
z=3
How do I solve this question

Answers
3y+1+56=180
3y+57-57=180-57
3y/3=123/3
Y=41

What’s the integral of 1/2
Answers
What are the coordinates of the midpoint of the line segment whose end points are (2, 6) and (10, 4)?
Answers
The midpoint of the line segment with endpoints (2, 6) and (10, 4) is (6, 5).
To find the midpoint of a line segment, we can use the midpoint formula, which states that the coordinates of the midpoint are the average of the coordinates of the endpoints.
Let's denote the coordinates of the first endpoint as (x1, y1) and the coordinates of the second endpoint as (x2, y2).
In this case, the first endpoint is (2, 6) with coordinates (x1, y1) = (2, 6), and the second endpoint is (10, 4) with coordinates (x2, y2) = (10, 4).
To find the midpoint, we use the midpoint formula:
Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2)
Plugging in the values, we have:
Midpoint = ((2 + 10) / 2, (6 + 4) / 2)
= (12 / 2, 10 / 2)
= (6, 5)
As a result, (6, 5) is the point on the line segment where the endpoints are (2, 6) and (10, 4) respectively.
for such more question on line segment
https://brainly.com/question/10496716
#SPJ8
Y
5+
4
No
-54-3-2
1
2 3 4
-3+
-47
5
Is (0,-5) a solution of the graphed system of inequalitie
Choose 1 answer:
А
Yes
В
No
MARK BRAINLIEST
20 POINTS PLEASE

Answers
Answer:
А Yes
Step-by-step explanation:
Graphic solutions of inequalities:
Generally, if the point is a painted region, it is a solution of the inequality, while if it is in a non-painted region, it is not a solution.
Is (0,-5) a solution of the graphed system of inequalities?
Point (0,-5) is 0 on the x-axis and -5 on the y-axis, which is painted, on the bottom part of the graphic, so it is a solutiom of the graphed system, and the correct answer is given by option A.
2. Evaluate (5+5√3i)^7 using DeMoivre’s theorem.
Write your answer in rectangular form.
Answers
Using DeMoivre’s theorem, the answer in regular form would be (5 + 5√3i)⁷ = -5000000 + 8660254.03i
How do we Evaluate (5+5√3i)⁷ using DeMoivre’s theorem?The De Moivre's Theorem is used to simplify the computation of powers and roots of complex numbers and is used in together with polar form.
Convert the complex number to polar form. The polar form of a complex number is z = r(cos θ + isin θ),
r = |z| magnitude of z
it becomes
r = √((5)² + (5√3)²) = 10
θ = arg(z) is the argument of z.
θ = atan2(b, a) = atan2(5√3, 5) = π/3
(5 + 5√3i) = 10 × (cos π/3 + i sin π/3)
De Moivre's theorem to raise the complex number to the 7th power
(5 + 5√3i)⁷
= 10⁷× (cos 7π/3 + i sin 7π/3)
= 10⁷ × (cos 2π/3 + i sin 2π/3)
Convert this back to rectangular form:
Real part = r cos θ = 10⁷× cos (2π/3) = -5000000
Imaginary part = r sin θ = 10⁷ × sin (2π/3) = 5000000√3 = 8660254.03i
∴ (5 + 5√3i)⁷ = -5000000 + 8660254.03i
Find more exercises on De Moivre's Theorem ;
https://brainly.com/question/28999678
#SPJ1
Answer:10^7 (1/2 - √3/2 i)
Step-by-step explanation:
To use DeMoivre's theorem, we first need to write the number in polar form. Let's find the magnitude and argument of the number:
Magnitude:
|5 + 5√(3i)| = √(5^2 + (5√3)^2) = √(25 + 75) = √100 = 10
Argument:
arg(5 + 5√(3i)) = tan^(-1)(√3) = π/3
So the number can be written in polar form as:
5 + 5√(3i) = 10(cos(π/3) + i sin(π/3))
Now we can use DeMoivre's theorem:
(5 + 5√(3i))^7 = 10^7 (cos(7π/3) + i sin(7π/3))
To simplify, we need to find the cosine and sine of 7π/3:
cos(7π/3) = cos(π/3) = 1/2
sin(7π/3) = -sin(π/3) = -√3/2
Explanation:
So the final answer in rectangular form is:
10^7 (1/2 - √3/2 i)
Anyone able to help with this?

Answers
\(W = 23.7°\)
Step-by-step explanation:
The formula given is the statement of Snell's law of refraction. We are given the following:
\(I_a = 1.0003\)
\(I_w = 1.3\)
\(A = 31.5°\)
So we need to find the angle of refraction W. Starting with Snell's law,
\(\dfrac{I_w}{I_a} = \dfrac{\sin A}{\sin W} \Rightarrow \sin W = \left(\dfrac{I_a}{I_w}\right)\sin A\)
Plugging in the given values, we get
\(\sin W = \left(\dfrac{1.0003}{1.3}\right)\sin{31.5°} = 0.402\)
Solving for the angle W, we then get
\(W = \sin^{-1}(0.402) = 23.7°\)
What is the rectangular form of 12(cos(Pi) + isin(Pi))?
12
-12
12 + i
–12 + i
Answers
The rectangular form of the polar expression \(12(cos\pi+ isin\pi)\) is -12
The given equation is:
\(12(cos\pi+ isin\pi)\)
The above equation is in polar form
Note that:
\(cos \pi = -1\\\\sin\pi = 0\)
Substituting \(cos \pi = -1\) and \(sin \pi = 0\) into the expression \(12(cos\pi+ isin\pi)\) in order to get the rectangular form of the expression
\(12(cos\pi+ isin\pi)\)
= 12(-1 + 1(0))
= 12 ( -1 + 0)
= 12(-1)
= -12
Therefore, the rectangular form of the polar expression \(12(cos\pi+ isin\pi)\) is -12
Learn more here: https://brainly.com/question/11731858
A) HL
B) Not enough information
C) AAS
D) SAS
Help please!

Answers
Answer:
SAS
Step-by-step explanation:
please help please...

Answers
The required coordinate of B' is B' = (4, -5), across the y-axis after reflection. Option A is correct.
What is the transformation of geometry over the coordinate plane?Transform the shapes on a coordinate plane by rotating, reflecting, or translating them.
here,
Given that a point B (-4, -5) is reflected across the y-axis, the Coordinate of image B' is to be determined.
Since the coordinate is reflected across the y-axis,
The equation of trasformation is given as,
(x , y) ⇒ (-x , y)
So, the image of B,
B' = (-(-4), -5)
B' = (4, -5)
Thus, the required coordinate of B' is B' = (4, -5), across the y-axis after reflection. Option A is correct.
Learn more about transformation here: https://brainly.com/question/18065245
#SPJ1
A bar of gold is 5.0 cm thick, 10.0 cm long and 2.0 cm wide. It has a mass of exactly 193.0 g. What is the density of gold?
Answers
Answer:
1.93g/cm^3 = density
Step-by-step explanation:
M = p • v
M = mass
p = density
v = volume
volume = l • w • h
volume = 10.0 cm • 2.0 cm • 5.0 cm
volume = 100 cm^3
193.0g = p • 100cm^3
divide each side by 100cm^3
1.93g/cm^3 = p
Best way to solve this type of equation Ax+by=c
Answers
The best way to solve an equation of the form Ax+by=c could be either substitution, completing the squares or graphical method depending on the type of equation given.
Quadratic equation
The equation in the form Ax+by=c is a quadratic problem which could be approached in different ways depending on the specific equation given and the information provided.
The methods of approach are substitution, completing the squares or graphical method which all have proven to be suitable ways to arrive at the solution.
Hence, either of the three methods are good ways to solve such equation.
Learn more on quadratic equations ; https://brainly.com/question/30164833
#SPJ1
At a bicycle shop, all the bicycles are on sale for $25 off the regular price. If p represents the regular price in dollars of a bicycle, which expression gives the sale price in dollars?
A. 25p
B. – 25p
C. p – 25
D. p + 25
Answers
Answer:
C
Step-by-step explanation:
P-25
what is 67% of 89.5?
Answers
Answer:
59.96
Step-by-step explanation:
when 67% if 89.5 is expressed in numbers,
\(\frac{67}{100}*89.5\\ \frac{5996.5}{100}\\ =59.96\)
A 12-ounce sports drink costs 0.96 and a 16-ounce sports drink costs $1.12. Which size is the best
buy? How much cheaper is it? Ratios
Answers
Answer:
It is better to buy the 16-ounce drink and it is 0.01 cent cheaper
Step-by-step explanation:
We have to find out how much each sports drinks cost per ounce.
0.96 ÷ 12 = 0.08 per ounce
1.12 ÷ 16 = 0.07 per ounce
It is better to buy the 16-ounce drink and it is 0.01 cent cheaper
Hope this Helps! :)
Have any questions? Ask below in the comments and I will try my best to answer.
-SGO
Select the correct answer. What is the solution to this equation? ( 1 4 ) x + 1 = 32 A. 3 2 B. - 2 C. - 7 2 D.
Answers
Answer: 2.214285714, probably B maybe? I'm not sure what D is.
Step-by-step explanation: (14)x + 1 = 32.
Your goal here is to get the x by itself so that you will know how much it is worth.
First step I would take is to subtract 1 from both sides to get rid of the one on the side with the x. What you do on one side is what you must do on the other side.
Now you have (14)x = 31
Next step I would take is divide both sides by 14 so that you can finally get the x by itself.
Now you have 2.214285714, so I would choose whatever answer that is closest to.
Helpoo i will mark you brainlist

Answers
Answer:
d) 28 in²
Step-by-step explanation:
A = bh
A = 7h
Find 'h' by using the Pythagorean Theorem:
3² + h² = 5²
9 + h² = 25
h² = 16
h = √16 = 4
A = 7×4 = 28
Answer:28
Step-by-step explanation:
Area of a parallelogram= bh
base-7
height- 4
using the Pythagorean theorem, \(5^{2}\) - \(3^{2}\)= \(\sqrt{16}\) = 4
7 * 4 = 28
I’ll give brainliest! Please help

Answers
Answer:
65
Step-by-step explanation:
The lines are parallell so m1 = m5, and m3=m8. 180-115 is 65
Determine whether it is possible to draw a triangle with the given side lengths so why or why not 11,10,20
Answers
Answer:
It is possible to draw a triangle with the given side lengths of 11, 10, and 20 because the sum of any two side lengths is greater than the length of the 3rd side as stated in the Triangle Inequality Theorem.
Explanation:
The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
So given the side lengths of 11, 10, and 20, let's see if it satisfies the above conditions;
\(\begin{gathered} 11+10=21\text{ and 21 > 20} \\ 11+20=31\text{ and 31 > 10} \\ 10+20=30\text{ and 30 > 11} \end{gathered}\)We can see from the above that the condition in the above theorem is satisfied, therefore, we can say that it is possible to draw a triangle with the given side lengths of 11, 10, and 20.