1. Mrs. Sanders farm is 413 acres. She divided the farm into 52 equal parts. How many acres are in each part? 2. Which of the following numbers are prime? a) 53 b) 12 c) 18 d) 28
Answers
Answer:
each part will have about 7.9 acres and the prime number is 53
Step-by-step explanation:
Related Questions
If 3 inch square is covered with 1inch squares how many of the 1 inch squares are needed? What is the area of the larger square
Answers
Answer:
9 1-inch squares will cover the bigger square. Its area is the same as the amount of squares needed, 9 inches.
the larger Area will be 9 square inch.
What is Area?Area is the entire amount of space occupied by a flat (2-D) surface or an object's form. On a sheet of paper, draw a square using a pencil. It has two dimensions. The area of a form on paper is the area that it occupies.
To cover a 3 inch square with 1 inch squares, we can arrange the 1 inch squares in a 3 by 3 grid.
So, we need 9 of the 1 inch squares to cover the 3 inch square.
The area of the larger square can be found by squaring the length of one of its sides.
Since the side length of the 3 inch square is 3 inches, the area of the larger square is:
Area = (side length)² = 3² = 9 square inches
Therefore, the larger Area will be 9 square inch.
Learn more about Area here:
https://brainly.com/question/27683633
#SPJ2
Which of the following is an improper integral?
A) the integral from 0 to 3 of the quotient of the quantity x plus 1 and the quantity 3 times x minus 2 dx
B) the integral from 1 to 3 of the quotient of the quantity x plus 1 and the quantity 3 times x minus 2 dx
C) the integral from negative 1 to 0 of the quotient of the quantity x plus 1 and the quantity 3 times x minus 2 dx
D) None of these
Answers
Answer:
A) \(\displaystyle \int\limits^3_0 {\frac{x + 1}{3x - 2}} \, dx\)
General Formulas and Concepts:
Calculus
Discontinuities
Removable (Hole) Jump Infinite (Asymptote)Integration
IntegralsDefinite IntegralsIntegration Constant CImproper IntegralsStep-by-step explanation:
Let's define our answer choices:
A) \(\displaystyle \int\limits^3_0 {\frac{x + 1}{3x - 2}} \, dx\)
B) \(\displaystyle \int\limits^3_1 {\frac{x + 1}{3x - 2}} \, dx\)
C) \(\displaystyle \int\limits^0_{-1} {\frac{x + 1}{3x - 2}} \, dx\)
D) None of these
We can see that we would have a infinite discontinuity if x = 2/3, as it would make the denominator 0 and we cannot divide by 0. Therefore, any interval that includes the value 2/3 would have to be rewritten and evaluated as an improper integral.
Of all the answer choices, we can see that A's bounds of integration (interval) includes x = 2/3.
∴ our answer is A.
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Integration
Book: College Calculus 10e
Wow...I forgot how to do this please help

Answers
Answer:
B. y = -6x+7
Step-by-step explanation:
change in x is positive 6 change in y is negative 1
6/-1 is the slope
-6 is the slope
find the limit. (if an answer does not exist, enter dne.) lim x → 0 tan−1(ln(x))
Answers
The answer doesn't exist for lim x → 0 tan−1(ln(x)).
To find the limit of the function as x approaches 0, lim(x→0) arctan(ln(x)), we need to analyze the behavior of the function near x = 0.
1. Consider the domain of the function. The natural logarithm ln(x) is only defined for x > 0, so we cannot evaluate the function at x = 0. However, we can still analyze the limit as x approaches 0 from the right.
2. As x approaches 0 from the right (x → 0+), the natural logarithm ln(x) approaches negative infinity (ln(x) → -∞).
3. The arctan function is continuous and has horizontal asymptotes at y = -π/2 and y = π/2. When its argument approaches negative infinity (ln(x) → -∞), the arctan function approaches its horizontal asymptote at y = -π/2.
Therefore, the limit of the function as x approaches 0 from the right is -π/2: lim(x→0+) arctan(ln(x)) = -π/2.
Since the function is not defined for x ≤ 0, the limit as x approaches 0 does not exist. Your answer is DNE (does not exist).
To learn more about limit: https://brainly.com/question/30679261
#SPJ11
can you please help me with number 4 please?

Answers
solve the equation 4x^3 + 32x^2 + 42x - 16 = 0, given that one root is equal to the sum of the other two roots
Answers
The solutions to the equation are x = -1, x = -8, and x = 1/2.
How to calculate the valueThe equation 4x³ + 32x² + 42x - 16 = 0 can be divided throuh by 2 as follows:
2x³ + 16x² + 21x - 8 = 0
We can test each of these possible roots by substituting them into the equation and seeing if we get 0. When we substitute -1, we get 0, so -1 is a root of the equation. We can then factor out (x + 1) from the equation to get:
(x + 1)(2x² + 15x - 8) = 0
We can then factor the quadratic 2x² + 15x - 8 by grouping to get:
(x + 8)(2x - 1) = 0
This gives us two more roots, x = -8 and x = 1/2.
Therefore, the solutions to the equation are x = -1, x = -8, and x = 1/2.
Learn more about equations on
https://brainly.com/question/2972832
#SPJ1
3. One leg of a right triangle measures 10 inches while the other leg measures 21 inches. What is the length of the hypotenuse?
A) c = 9in
B) c = 11in
C) c = 12in
D) c = 7in
4. If the length of the hypotenuse is 10m and its base leg is 6m, what is the length of its remaining leg?
A) a = 8m
B) a = 9m
C) a = 12m
D) a = 10m
5. The altitudes of a right triangle has a length of 32cm. It’s hypotenuse measures 9cm. How long is its base leg?
A) b = 5cm
B) b = 7cm
C) b = 6cm
D) b = 9cm
6. Ben pushes a stick in the ground next to a flag pole so that its measure from the ground is 1 foot. The stick casts a shadow of 4 feet while the flag pole casts a parallel shadow of 60 feet. How tall is the
Answers
Step-by-step explanation:
Pythagoras formula for the relation of the side lengths in a right-angled triangle :
c² = a² + b²
c is the Hypotenuse, the side opposite of the 90 degree angle.
a and b are the "legs".
3.
c² = 10² + 21² = 100 + 441 = 541
c = sqrt(541) = 23.2594066...in
so, none of the provided answers. are you sure you put the right numbers ? maybe the second leg is sqrt(21) instead of 21 ? because then it would be
c² = 10² + sqrt(21)² = 100 + 21 = 121
c = 11in
4.
10² = a² + 6²
100 = a² + 36
64 = a²
a = 8 m
5.
again, there must be something wrong. the height of the triangle cannot be longer than the legs of the triangle.
given the answer options of 5 - 9 cm it cannot be 32cm. maybe you mean 3.2 cm ?
also interesting that it says "attitudes" - plural. what do you mean by that ?
because there is something else missing. like how long are the segments of the Hypotenuse where the height (or altitude) is touching the Hypotenuse ?
with just the Hypotenuse length and the height length we cannot calculate the other parts of the triangle, because we can move the height freely along the Hypotenuse and draw fitting right-angled triangles on that "skeleton".
6.
similar triangles. that means the lengths of corresponding lines (like sides or heights) are all in relation with the same scaling factor.
so, the small triangle has its "height" side of 1 ft, and multiplying with the scaling factor would then give us the height of the flag pole.
what is the scaling factor ? we get that from the pair of corresponding sides we already know : the shadows.
going from the small to the large triangle we have to transform 4ft into 60ft.
what do I have to multiply 4 with to get 60 ?
4 × x = 60
x = 60/4 = 15
so, the flag pole is
15×1 = 15ft tall.
In the course, we mentioned that the problem of deciding whether a given positive integer n is prime is solvable in polynomial time but that the proof is highly nontrivial. This is based on the assumption that n is given in base 2, i.e. as a binary string. In this problem, we will see that primality has a much simpler algorithm, if we change the base in which we represent n; so the complexity of a problem does depend on how we represent the input. Assume that n is represented in unary notation: namely, the string that represents n is 1
n
(the string of n ones.) In this representation, show that the Eratosthenes' Sieve which checks whether n is divisble by any integer ≤
n
runs in time O(n
2
) when implemented on a Turing machine. (You may assume that there exists a Turing machine which, given n, computes ⌈
n
⌉.
Answers
1)The time complexity of the Eratosthenes' Sieve algorithm in unary notation is O(n) + O(n) + O(n) + O(1) = O(n). 2)when implemented on a Turing machine with unary notation input, the Eratosthenes' Sieve algorithm runs in O(n) time complexity, not O(n^2)
In unary notation, a positive integer n is represented by a string of n ones, denoted as '1n'. For example, 5 is represented as '11111' and 10 is represented as '1111111111'.
Eratosthenes' Sieve is an algorithm used to determine whether a given number n is prime by checking its divisibility with integers up to √n. To analyze the time complexity of the Sieve when implemented on a Turing machine with unary notation input, we need to understand the steps involved in the algorithm.
1. Input: The input to the Sieve is the number n represented in unary notation, '1n'.
2. Initialization: Initialize a boolean array of size n, initially assuming all numbers as prime.
3. Sieve: For each number from 2 to √n, check if it is marked as prime. If it is prime, mark all its multiples as non-prime in the boolean array.
4. Primality Check: Finally, check if the number n is marked as prime in the boolean array. If it is, then n is prime; otherwise, it is not prime.
Let's analyze the time complexity of each step:
1. Input: Representing the number n in unary notation takes O(n) time.
2. Initialization: Initializing the boolean array of size n takes O(n) time.
3. Sieve: In unary notation, the value of n is represented by a string of n ones. So, iterating from 2 to √n would require iterating from '11' to '1√n'. Since we are considering unary notation, the number of iterations required will be proportional to n itself. Therefore, this step takes O(n) time.
4. Primality Check: Checking whether n is marked as prime in the boolean array takes constant time, i.e., O(1).
Overall, the time complexity of the Eratosthenes' Sieve algorithm in unary notation is O(n) + O(n) + O(n) + O(1) = O(n).
Therefore, when implemented on a Turing machine with unary notation input, the Eratosthenes' Sieve algorithm runs in O(n) time complexity, not O(n^2) as mentioned in the problem statement.
Learn more about Unary notation here:
brainly.com/question/32269179
#SPJ11
write out the form of the partial fraction decomposition of the function (see example). do not determine the numerical values of the coefficients. (a) 1 (x2 − 2x)(x 9)2
Answers
The partial fraction decomposition of the function "(x - 20)/(x² + x - 20)" is A/(x + 5) + B/(x - 4) .
The function of which we have to find the partial fraction decomposition is (x - 20)/(x² + x - 20) ;
In order to find the partial fraction decomposition of the function (x - 20)/(x² + x - 20),
We factor the denominator into linear factors ;
We get ;
⇒ x² + x - 20 = (x + 5)(x - 4)
Now, we use the partial fraction decomposition method , to write
⇒ (x - 20)/(x² + x - 20) = (x - 20)/(x + 5)(x - 4)
⇒ (x - 20)/(x² + x - 20) = A/(x + 5) + B/(x - 4)
Therefore , the partial fraction decomposition form is A/(x + 5) + B/(x - 4) .
Learn more about Partial Fraction Decomposition here
https://brainly.com/question/29762169
#SPJ4
The given question is incomplete , the complete question is
Write out the form of the partial fraction decomposition of the function . Do not determine the numerical values of the coefficients. (x - 20)/(x² + x - 20) .
Therefore, the sign of the product (x3)4(x - 4)3(x 6)6-f(x) depends only on the sign of (x-4)3 (assuming x#-3). ÎfX<4, then(x-4)31s negative . Enegativel, and so the sign of (x + 3)"(x-4)3(x-6)#2 f(x) is |negative P negative! . Therefore, rx) is decreasing decreasing Step 4 If x > 4, then (x-4)з is positive Y , , and so the sign of (x + 3)4(x-4)3(x-6)#2 rx) is positive (again assuming x #-3). Therefore, f(x) is lincreasing Y , Therefore, fis increasing on the following interval. (Enter your answer in interval notation.)
Answers
The given function is f(x) = (x+3)^4 * (x-4)^3 * (x-6)^6. The interval on which f(x) is increasing is (4, ∞).
To determine the intervals on which f(x) is increasing or decreasing, we need to analyze the sign of f'(x), the first derivative of f(x). In this case, f'(x) can be calculated using the product and chain rules of differentiation:
f'(x) = 4(x+3)^3 * (x-4)^3 * (x-6)^6 + 3(x+3)^4 * (x-4)^2 * (x-6)^6 + 6(x+3)^4 * (x-4)^3 * (x-6)^5
Simplifying f'(x) and factoring out common terms, we get:
f'(x) = (x+3)^3 * (x-4)^2 * (x-6)^5 * [4(x-6) + 3(x+3)(x-4) + 6(x-4)]
We can now analyze the sign of f'(x) for different values of x:
If x < 4, then (x-4)^3 is negative, and hence f'(x) is negative. This implies that f(x) is decreasing on the interval (-∞, 4).If x = 4, then f'(x) is zero, which indicates a possible local extremum at x = 4.If 4 < x < 6, then (x-4)^3 is positive and (x-6) is negative, resulting in a negative f'(x). Thus, f(x) is decreasing on the interval (4, 6).If x > 6, then (x-4)^3 and (x-6) is positive, leading to a positive f'(x). Therefore, f(x) is increasing on the interval (6, ∞).Thus, the interval on which f(x) is increasing is (4, ∞).
To learn more about chain rules, visit:
https://brainly.com/question/22882675
#SPJ11
The given function is f(x) = (x+3)^4 * (x-4)^3 * (x-6)^6. The interval on which f(x) is increasing is (4, ∞).
To determine the intervals on which f(x) is increasing or decreasing, we need to analyze the sign of f'(x), the first derivative of f(x). In this case, f'(x) can be calculated using the product and chain rules of differentiation:
f'(x) = 4(x+3)^3 * (x-4)^3 * (x-6)^6 + 3(x+3)^4 * (x-4)^2 * (x-6)^6 + 6(x+3)^4 * (x-4)^3 * (x-6)^5
Simplifying f'(x) and factoring out common terms, we get:
f'(x) = (x+3)^3 * (x-4)^2 * (x-6)^5 * [4(x-6) + 3(x+3)(x-4) + 6(x-4)]
We can now analyze the sign of f'(x) for different values of x:
If x < 4, then (x-4)^3 is negative, and hence f'(x) is negative. This implies that f(x) is decreasing on the interval (-∞, 4).If x = 4, then f'(x) is zero, which indicates a possible local extremum at x = 4.If 4 < x < 6, then (x-4)^3 is positive and (x-6) is negative, resulting in a negative f'(x). Thus, f(x) is decreasing on the interval (4, 6).If x > 6, then (x-4)^3 and (x-6) is positive, leading to a positive f'(x). Therefore, f(x) is increasing on the interval (6, ∞).Thus, the interval on which f(x) is increasing is (4, ∞).
To learn more about chain rules, visit:
https://brainly.com/question/22882675
#SPJ11
If a snowboarder tries to do a 360 but makes it only 3/4 of the way around, how many degrees would that be?
Answers
Multiply 360 by 3/4
360 x 3/4 = (360 x3)/4 = 1080/4 = 270
Answer : 270 degrees
The concepts of right and wrong: (a) are the basic value concepts.(b) are used primarily to evaluate the morality of actions. (c) are used in the moral evaluation of persons as well as in the evaluation of things, experiences, and states of affairs. (d) a and b.(e) a and c
Answers
The concepts of right and wrong encompass both the basic value concepts and the evaluation of morality in actions, as well as the evaluation of persons, things, experiences, and states of affairs. Therefore, the correct option is (e) "a and c."
The concepts of right and wrong are fundamental to ethics and moral reasoning. They serve as foundational value concepts, guiding individuals in distinguishing between what is considered morally good (right) and morally bad (wrong).
These concepts are not limited to evaluating the morality of actions alone (option b), but they also extend to evaluating the moral character of individuals and the ethical aspects of various entities, such as things, experiences, and states of affairs (option c). The moral evaluation of persons encompasses judgments about their intentions, virtues, and overall ethical conduct.
Hence, both options a and c accurately capture the comprehensive nature of the concepts of right and wrong.
To learn more about states of affairs click here: brainly.com/question/14757153
#SPJ11
What type of sample does personal experience generate?.
Answers
Personal experience generates firsthand knowledge that is derived from an individual's direct involvement or observation of a particular event, situation, or phenomenon. This type of sample is unique to each person and provides a subjective understanding of the subject matter.
Personal experience is an essential source of learning and understanding as it allows individuals to gain insight, develop skills, and form opinions based on their own encounters. It can provide a deep understanding of emotions, perspectives, and nuances that cannot be fully grasped through secondhand information. Personal experiences are often considered valuable as they offer authenticity and a sense of relatability, enabling individuals to connect with others on a personal level. Additionally, personal experiences can serve as a foundation for personal growth and development, shaping one's beliefs, values, and decision-making processes.
learn more about decision-making here
brainly.com/question/28900762
#SPJ11
HELP ASP!!!!!!
The explicit rule for a sequence and one of the specific terms is given. Find the position of the given
term.
f(n) = 1.25n +3.75; 20
20 is the
th term.

Answers
Answer:
the 13th term, if you plug in 13 for n and solve you would get 20 :)
Answer:
13th term
Step-by-step explanation:

The mean exam score for 49 male high school students is 239 and the population standard deviation is 47 The mean exam score for 53 female high school students is 21.1 and the population standard deviation is 4.3. At α=001, can you reject the claim that male and female high school students ha equal exam scores? Complete parts (a) through (e). Click here to view page 1 of the standard normal distribution table. Click here to view. page 2 of the standard normal distribution table. A. Male high school students have lower exam scores than female students B. Male and temale high school students have different exam scores. C. Male and female high school students have equal exam scores D. Male high school students have greater exam scores than female students
Answers
Comparing the means of the two samples, we find that the difference between the means is significant. Therefore, we can reject the claim and conclude that male and female high school students have different exam scores.
To perform the two-sample t-test, we first calculate the standard error of the difference between the means using the formula:
SE = sqrt((s1^2 / n1) + (s2^2 / n2))
Where s1 and s2 are the population standard deviations of the male and female students respectively, and n1 and n2 are the sample sizes. Plugging in the values, we have:
SE = sqrt((47^2 / 49) + (4.3^2 / 53))
Next, we calculate the t-statistic using the formula:
t = (x1 - x2) / SE
Where x1 and x2 are the sample means. Plugging in the values, we have:
t = (239 - 21.1) / SE
We can then compare the t-value to the critical t-value at α = 0.01 with degrees of freedom equal to the sum of the sample sizes minus 2. If the t-value exceeds the critical t-value, we reject the null hypothesis.
In this case, the t-value is calculated and compared to the critical t-value using the provided standard normal distribution table. Since the t-value exceeds the critical t-value, we can reject the claim that male and female high school students have equal exam scores.
Therefore, the correct answer is:
B. Male and female high school students have different exam scores.
Learn more about hypothesis testing here: brainly.com/question/17099835
#SPJ11
Maya needs to mail 17 books to her aunt. Each of the boxes she has can hold 5 books. How many boxes will Maya need to mail all of the books?
Answers
An airplane is at 32000 feet above sea level and the seeds at an average rate of 1000 feet per minute how many minutes will it take for the airplane to land at an airport 3000 feet above sea level
Answers
Answer:
29 minutes
Step-by-step explanation:
Let
x = number of minutes
y = the height of the airplane above sea level in feet
y = 32,000 - 1000x
y = 3,000
Therefore,
y = 32,000 - 1000x
3,000 = 32,000 - 1000x
3,000 - 32,000 = -1000x
-29,000 = -1,000x
x = -29,000 / -1,000
x = 29 minutes
it will take 29 minutes for the airplane to land at an airport 3000 feet above sea level
Please help me, thank you :)

Answers
Answer:
14+14 + 4pi= 28 + 4pi
\(\pi\)
Area of rectangle = 14*4= 56
Area of circle = 4pi
Add them together. 56 + 4pi = 68.6
let x be an ordered set. if y is a proper subset of x that is convex in x, does it follow that y is an interval or a ray in x?
Answers
No, it does not follow that y is an interval or a ray in x. A convex subset of an ordered set is a set that contains all the points between any two points in the set.
This means that a convex subset of an ordered set could be a collection of points, it could be an interval, or it could be a ray. A proper subset of an ordered set is any subset except the entire set, so a proper subset of an ordered set could be any of these possibilities.
Therefore, while a proper subset of an ordered set that is convex in that set must be a collection of points, an interval, or a ray, it does not necessarily have to be one of those three options.
know more about ray here
https://brainly.com/question/17491571#
#SPJ11
A side of the triangle below has been extended to form an exterior angle of 132°. Find
the value of a.
132°
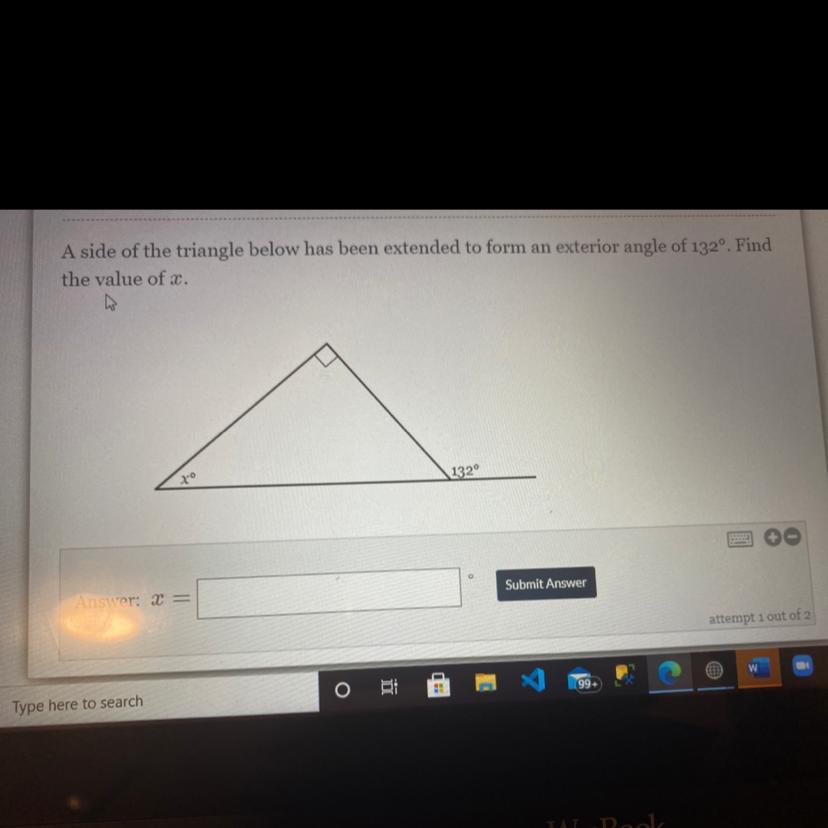
Answers
Answer:
x=42
Step-by-step explanation:
so they u the exterior angle is 132
line makes 180 degree
180-132 =48
now they tell u a right angle
that is 90
triangles interior angles add up to 180
180-90-48=
42
Brainliest Please\(x + 90 = 132\)
(exterior angle property)
\(x = 132 - 90\)
\(x = 42\)
Find the slope and y-intercept from the graph. Then enter the equation for the graph in slope-intercept form.
The table numbers are (0,9) (1,13) (2,17) (3,21) (4,25)

Answers
Answer: y=4x+9
Slope = 4
Step-by-step explanation:
y2-y1/x2-x1
Given 3,21 and 4,25
25-21/4-3 = 4/1 = 4
Slope = 4
You can use the point-slope formula to get the following equation in slope-intercept formula.
y-y1 = m(x-x1)
(4,25)
->
y-25=4(x-4)
Distribute
y-25=4x-16
Cancel 25
y=4x+9
use the exponent rule to simplify

Answers
Answer:
\(y^{-5}\)
Step-by-step explanation:
The Exponent Quotient Rule states that if two terms of the same base are being divided by each other, then the simplified expression is the base to the first power subtracted by the second power. As an algebraic equation, that would be \(\frac{x^{a} }{x^{b} } =x^{a-b\), where \(x\) is the common base and \(a\) and \(b\) are the exponents.
In this case, \(x=y\), \(a=2\), and \(b=7\), so we know that \(\frac{y^{2} }{y^{7} } =y^{2-7}=y^{-5}\). Hope this helps!
lot the first n terms of the sequence. a1 = 1, a2 = 2, and for n ≥ 2, an = 1 2 (an − 1 an − 2); n = 30
Does the graphical evidence suggest that the sequence converges or diverges?
Since the terms ---Select--- oscillate, but do not approach one single value oscillate above and below 8/3 become arbitrarily large tend to approach 0 , the sequence appears to ---Select--- converge diverge .
Answers
Since the terms oscillate but do not approach one single value, the sequence appears to diverge
To find the first n terms of the sequence with the given terms a1 = 1, a2 = 2, and the rule for n ≥ 2, \(an = 1/2((an-1)(an-2))\), let's use n = 30.
1. Start with the given terms: a1 = 1 and a2 = 2.
2. Use the formula to find the next terms, up to n = 30.
It's important to calculate some of the terms in the sequence to determine if it converges or diverges. However, due to the character limit, I can't list all 30 terms here. Nevertheless, let's calculate the first few terms:
⇒ \(a_{3}= \frac{1}{2} ((a_{3})(a_{3})\)
= \(= \frac{1}{2} ((2)(1))\)
= 1
⇒\(= a_{4}= \frac{1}{2} ((a_{3})(a_{2}))\)
= \(\frac{1}{2} ((1)(2))\)
= 1
⇒\(a_{5}= \frac{1}{2} ((a_{4}) (a_{3}))\)
\(=\frac{1}{2} ((1)(1))\)
= 0.5
By examining the terms of the sequence, we can see that they oscillate but do not approach one single value. Therefore, the sequence appears to diverge.
Since the terms oscillate but do not approach one single value, the sequence appears to diverge.
To know more about "Convergent series and Divergent series" refer here:
https://brainly.com/question/15415793#
#SPJ11
How many solutions does the quadratic system shown below have ?

Answers
help.
Find the area of the figure.

Answers
the area of the triangle is 7.5
Three times a number lies between negative three and six in digits
Answers
Answer:
-3 ≤ 3x ≤ 6
To solve for "x", we can divide each part of the inequality by 3:
-1 ≤ x ≤ 2
Therefore, the number "x" must lie between -1 and 2 in order to satisfy the condition in the sentence.
Step-by-step explanation:
Find the area of this

Answers
Answer:
124
Step-by-step explanation:
The dimensions of a rectangle are x+3 and x+4. The area of the rectangle is 72. Set up an equation that models this rectangle and solve in order to determine the value of x.
Answers
Answer: x = 5
Step-by-step explanation:
The area of a rectangle is the length times the width. Since the dimensions are given as functions of x, youre going to have to use FOIL to combine them, then set that answer equal to the given value of 72.
l*w = (x+3)*(x+4) = x^2 + 7x +12 = 72
Subtract 72 on both sides. There is a reason why we'll do this instead of subtracting 12. The quadratic formula will help us to solve for x.
x^2 + 7x - 60 = 0
Apply the quadratic formula
\(\frac{-7 (+/-)\sqrt{7^2-(4)*(1)*(-60} }{2*1} =\frac{-7(+/-)17}{2}\)
We cant have a negative x value because that would result in negative dimensions and a negative area, which is impossible in this context. So you want to add the 17 instead of subtracting it.
x = 5 and x = -12
An alternate way is just factoring the trinomial to:
(x+12)(x-5) = 0
three-fourths the square of a number
O 3 (4x^2)
O (3/4)(2x)
O 3(x^4)
0 (3/4)X^2
What’s the answer??
Answers
Tell me the linear equation for point-slope form? SOMEONE HELP ME