1. Describe how to translate a figure with the algebraic representation (x,y) → (x + 3, y-5)? Use the sentence stem below.To translate a figure using the rule (x, y)----> (x-3, y-5), first you would.......
Answers
To translate a figure using the rule (x, y)----> (x+3, y-5), first you would locate the coordinates of the vertices
secondly, add 3 from the x -coordinates and then subtract 5 from the y coordinates
Thirdly, After the translation of its vertices, connect the vertices to form the figure
Related Questions
Solve the following system of equations a2+b2 ; 3a2 -2ab-b2
Answers
The system has an infinite number of solutions, but the only solution is (a, b) = (0, 0).
The given system of equations can be solved using the substitution method. We can begin by solving the first equation,\(a^2 + b^2\), for either a or b. Let's solve for a:
\(a^2 + b^2 = 0\)
\(a^2 + b^2 = 0\)
\(a^2 = -b^2\)
\(a = \pm\sqrt(-b^2)\)
We can substitute this expression for a into the second equation, \(3a^2 - 2ab - b^2 = 0\), and simplify:
\(3(\pm\sqrt(-b^2))^2 - 2(\pm\sqrt(-b^2))b - b^2 = 0\)
\(3b^2 - 2b^2 - b^2 = 0\)
0 = 0
Since 0 = 0, this means that the system of equations has an infinite number of solutions. In other words, any values of a and b that satisfy the equation \(a^2 + b^2 = 0\) will also satisfy the equation \(3a^2 - 2ab - b^2 = 0\)
However, the equation \(a^2 + b^2 = 0\) only has a single solution, which is a = b = 0. Therefore, the solution to the system of equations is (a, b) = (0, 0).
Learn more about substitution here:
brainly.com/question/22340165
#SPJ1
Which of the following functions is graphed below?
O A. y -** 2-3
B. y - 4-3
C. y - x - 2-3
OD. y - x - 223

Answers
Using translation concepts, it is found that the function graphed is defined by:
D. y = |x - 2| + 3.
What is a translation?A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction in it's definition.
In this problem, the function has the format of the absolute value function, y = |x|, which has vertex at (0,0). Here, the vertex is at (2,3), that is, the function was shifted:
2 units to the right, that is, x -> x + 2.3 units up, that is, y -> y + 3.Hence the definition is given by:
D. y = |x - 2| + 3.
More can be learned about translation concepts at https://brainly.com/question/4521517
#SPJ1
Bill works as a tutor for an hour and as a waiter for an hour. This month, he worked a combined total of hours at his two jobs. Let be the number of hours Bill worked as a tutor this month. Write an expression for the combined total dollar amount he earned this month.
Answers
Answer:
31
Step-by-step explanation:
The degree of the expression 4x5ymz is 10. What is the value of m?
Answers
Answer:
the answer is 4
Step-by-step explanation:
help! please give 35 points

Answers
The area of the composite figure is 378.5 square feets.
How to find the total area of the figure?We can decompose this into a rectangle of 30ft by 10ft and a circle whose diameter is 10ft.
Remember that the area of a rectangle of width W and length L is given by:
A = L*W
So the area of this rectangle is:
A = 30ft*10ft = 300ft²
And the area of a circle whose diameter D is:
A = 3.14*(D/2)²
So in this case the area of the circle is:
A = 3.14*(10ft/2)²
A = 3.14*(5ft)² = 78.5 ft²
Then the total area of the composite figure is:
area = 300ft² + 78.5 ft²
area = 378.5 ft²
Learn more about area at:
https://brainly.com/question/24487155
#SPJ1
all points having an x-coordinate of 1 whose distance from the point (-3,-6) is 5
Answers
Answer:
\(They'll \: be \: on \: the \: circle:\)
\((x+3)^2+(y+6)^2=25\)
\(x=1\)
\((y+6)^2=9\)
\(y + 6 = 3\)
\(y = -3\)
\((1,-3)\)
\(y + 6 = -3\)
\(y = -9\)
\((1,-9)\)
Step-by-step explanation:
\(Thank \: you!!!!!!\)
(12sin(pi/2x)*lnx)/((x³+5)(x-1))
lim as x approaches 1
Answers
The limit of the given function as x approaches 1 is 0.
To find the limit of the given function as x approaches 1, we need to evaluate the expression by substituting x = 1. Let's break it down step by step:
1. Begin by substituting x = 1 into the numerator:
\(\[12\sin\left(\frac{\pi}{2}\cdot 1\right)\ln(1) = 12\sin\left(\frac{\pi}{2}\right)\ln(1) = 12(1)\cdot 0 = 0\]\)
2. Now, substitute x = 1 into the denominator:
(1³ + 5)(1 - 1) = 6(0) = 0
3. Finally, divide the numerator by the denominator:
0/0
The result is an indeterminate form of 0/0, which means further analysis is required to determine the limit. To evaluate this limit, we can apply L'Hôpital's rule, which states that if we have an indeterminate form 0/0, we can take the derivative of the numerator and denominator and then evaluate the limit again. Applying L'Hôpital's rule:
4. Take the derivative of the numerator:
\(\[\frac{d}{dx}\left(12\sin\left(\frac{\pi}{2}x\right)\ln(x)\right) = 12\left(\cos\left(\frac{\pi}{2}x\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{-1}{x} + \frac{\sin\left(\frac{\pi}{2}x\right)\ln(x)}{x}\right)\]\)
5. Take the derivative of the denominator:
\(\[\frac{d}{dx}\left((x^3 + 5)(x - 1)\right) = \frac{d}{dx}\left(x^4 - x^3 + 5x - 5\right) = 4x^3 - 3x^2 + 5\]\)
6. Substitute x = 1 into the derivatives:
Numerator: \(\[12\left(\cos\left(\frac{\pi}{2}\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{-1}{1} + \sin\left(\frac{\pi}{2}\right) \cdot \frac{\ln(1)}{1}\right) = 0\]\)
Denominator: 4(1)³ - 3(1)² + 5 = 4 - 3 + 5 = 6
7. Now, reevaluate the limit using the derivatives:
lim as x approaches 1 of \(\[\frac{{12\left(\cos\left(\frac{\pi}{2}x\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{{-1}}{{x}} + \sin\left(\frac{\pi}{2}x\right) \cdot \frac{{\ln(x)}}{{x}}\right)}}{{4x^3 - 3x^2 + 5}}\]\)
= 0 / 6
= 0
Therefore, the limit of the given function as x approaches 1 is 0.
For more such questions on L'Hôpital's rule
https://brainly.com/question/24116045
#SPJ8
(a) Suppose that a person has an average heart rate of 72.0 beats/min. How many beats does he or she have in 2.0 y
Answers
Answer:
\(7.56\times 10^7\ \text{beats}\)
Step-by-step explanation:
It is given that,
A person has an average heart rate of 72.0 beats/min.
We need to find how many beats does he or she have in 2.0 years, t = 2 Y
Converting years to min.
\(t=2\text{year}\times \dfrac{365\ \text{days}}{\text{year}}\times 24\dfrac{h}{\text{day}}\times \dfrac{60\text{min}}{\text{hour}}\\\\t=1051200\ \text{min}\)
So, no of beats in 2 years is given by :
\(b=72\ \text{beats/min}\times 1051200\ \text{min}\\\\b=7.56\times 10^7\ \text{beats}\)
Hence, the required answer is \(7.56\times 10^7\ \text{beats}\).
If x > 1, then which of the following has the least value
Answers
PLEASE HELP MEEEEEEEEEE

Answers
Answer:
Step-by-step explanation:
1 pound of potato salad costs 2.96
0.75 pounds of potato salad costs x
1/0.75 = 2.96/x Cross multiply
x = 0.75 * 2.96
x = 2.22
0.75 pounds of potato salad costs 2.22 dollars.
A precise statement of the qualities of an idea, object, or process is called a
O A. theorem
O B. proof
C. definition
D. common notion
Answers
Answer:
C. definition
Step-by-step explanation:
A precise statement of the qualities of an idea, object, or process is called a definition. Hence, option (C) is answer.
the question b/4+2= -1
Answers
Answer:
b = -3/4
Step-by-step explanation:
b/4 = -3
b = -3/4
\(\frac{b}{4}+2 = -1\)
\(\frac{b}{4}=-1 -2\\ \frac{b}{4}=-3\\ b=-12\)
b= -12 so that hope that helps!
A travel agent makes the hypothesis:
More holiday refunds are given in the winter than in the summer.
a) Use the information in the bar chart to work out:
- i) the mean number of refunds given in the summer.
- ii) the mean number of refunds given in the winter.
b) Does your answer to part a) support the hypothesis or not?

Answers
a)
i) The mean number of refunds given in the summer is 21.
ii) The mean number of refunds given in the winter is 20.
b) The answer to part a) does NOT support the hypothesis.
How is this so?To calculate the mean number of refunds given in the summer and winter,we need to find the average of the values for each season over the given years. Let's calculate -
a) Mean number of refunds given in the summer -
(20 + 15 + 10 + 15 + 32 + 34) / 6
= 126 / 6
= 21
b) Mean number of refunds given in the winter -
(24 + 10 + 15 + 18 + 26 + 27) / 6
= 120 / 6
= 20
The mean number of refunds given in thesummer is 21, and the mean number of refunds given in the winter is 20.
b) Based on the calculated means, the answer to part a) does NOT support the hypothesis.
The mean number of refunds given in the summer (21) is greater than the mean number of refunds given in thewinter (20), indicating that more refunds are given in the summer than in the winter, contrary to the hypothesis.
Learn more about hypothesis at:
https://brainly.com/question/606806
#SPJ1
Given that ABCD is a rhombus, find the value of x. 4 (X +40) A. 75 B. 52 C. 25 D. 46 F. 26

Answers
the value of variable x in the rhombus is Option (c) 25.
Definition of a rhombusA parallelogram is a particular instance of a rhombus. opposite sides and angles of the rhombus are parallel and equal. The rhombus has equal-length sides on each side, and its diagonals meet at right angles to form its shape as square. The rhombus is sometimes called as a diamond or rhombus.
Let O be the intersection point of the line AC and the line BD in the rhombus.
This two lines intersect at a 90° angle in the center. ( Property of Rhombus)
∠AOD=90°
According to the question:∠AOD+∠OAD+∠ODA=180° (triangle sum property)
90°+x+x+40°=180°
2x=180°-130°
x=25
Hence the value of x=25.
To know more about parallelogram, visit:
https://brainly.com/question/19187448
#SPJ1
12x + 4y = -8 solve using substration method
Answers
Step-by-step explanation:
12-(4y)That's how you do it
please help me with my geometry i cant fail this class or i’ll have to move out of my parents house :(

Answers
Applying the tangent and the circle theorems, we have:
22. x ≈ 9.4; 23. Perimeter of triangle GHI = 168 units
24. m<NSR = 110°; 25. x = 10
How to Find the Missing Measures Using Circle and Tangent Theorems?22. Based on the tangent theorem, the triangle is a right triangle since the line is tangent to the radius of the circle. Therefore, based on the Pythagorean theorem, we have:
x = √[(7.4 + 4.6)² - 7.4²]
x ≈ 9.4
23. JH and HK are tangents, therefore they are equal. Thus:
7x + 4 = 13x - 20
7x - 13x = -4 - 20
-6x = -24
x = 4
Perimeter = GI + GJ + JH + HK + KI
GI = 52
HK = JH = 7x + 4 = 7(4) + 4 = 32
KI = 15
GJ = 52 - 15 = 37
Perimeter of triangle GHI = 52 + 37 + 32 + 32 + 15 = 168 units
24. Based on the angle of intersecting chords theorem, we have:
m<NSR = 1/2(170 + 50)
m<NSR = 110°
25. Based on the inscribed angle theorem, we have:
2(4x - 5) + 290 = 360
Solve for x:
8x - 10 + 290 = 360
8x = 360 - 280
8x = 80
x = 10
Learn more about the tangent theorems on:
https://brainly.com/question/28039126
#SPJ1
Determine the mean, median, mode and midrange for the following data:
13 15 18 18 21
Your answers should be exact numerical values.
The mean of the data is
The median of the data is
The mode of the data is
The midrange of the data is
Answers
The Mean is 17, Median is 18, Mode is 18 and, Midrange is 17.
The Mean is defined as the ratio of sum of numbers present in the data to the total numbers present in the data. Median is defined as the ratio of sum of middle numbers present in the data. Mode is defined as the most recurring number present in the data. Midrange is the ratio of the largest and smallest number in the data to 2.
Let's see how to calculate Mean, Median, Mode and Midrange.
Mean = 13 + 15 + 18 + 18 + 21 / 5
Mean = 85 / 5
Mean = 17
Median = 18 (as it is the middle term of the data)
Mode = 18 (as it is most recurring number)
Midrange = 21 + 13 / 2
Midrange = 34 / 2
Midrange = 17
Therefore, The Mean is 17, Median is 18, Mode is 18 and, Midrange is 17.
To study more about Mean, Median Mode:
https://brainly.com/question/14532771
https://brainly.com/question/542771
Yara has 2 rectangular gardens in her backyard. The smaller garden is 1/2 foot long and 2/3
foot wide. The larger garden is 4 feet long and feet wide. What is the area of the smaller
garden in square feet? What is the area of the larger garden in square feet?
Answers
Dimension of smaller garden :
l = 1/2 ft.
b = 2/3 ft.
Dimension of bigger garden :
L = 4 ft.
Let , breadth be x ft.
We know , area is given by :
Area = L×B.
Area of small garden = \(\dfrac{1}{2}\times\dfrac{2}{3}=\dfrac{1}{3}\ ft^2\)
Area of big garden \(=4\times x=4x\ ft^2\)
Hence, this is the required solution.
what is the area of this figure

Answers
Answer:
Step-by-step explanation:
48
Answer:
142 sq ft
Step-by-step explanation:
i drew lines to separate into 3 rectangles:
- 4 x 1' rect = 4 sq ft
- 5 x 6' rect = 30 sq ft
- 6* x 18 rect = 108 sq ft
* the 6 comes from 15 - (4 + 5)
total area = 4 + 30 + 108 = 142
help......................

Answers
Where the above relations are given, note that Options A, D, and E are the relations that represents a function. The others are just relations.
How do you identify the relation that represents a function?To distinguish a function from a relation, look to see if any of the x values are repeated; if not, the relationship is a function. If some x values are repeated but the accompanying y values differ, we have a relation rather than a function.
Note that where you are given domain and range, only the range is represented on the x-axis.
Some of the x values may be seen repeated in B, and C.
How is this so?
B) In a coordinate system, values are represented as (x, y). so
In relations, B 2 is repeated twice to in connection with -5, and -6. That is:
(2, -5) , (2, -6)
Since two is x, then its repetition nullified the relation as a function.
C) On table indicated on C, it is much easier to identify the x and y values. As is seen, -3 is repeated twice in connection with 4 and 2. Thus, its repetition nullified the relation as a function.
As a result, Options A, D, and E are the relations that represent a function.
Learn more about function at:
https://brainly.com/question/30721594
#SPJ1
Which of the following is a solution to this inequality?
y<2/3x+2
(0, 3)
(−3, 1)
(3, 5)
(1, 2)
Answers
Answer:
(d) (1, 2)
Step-by-step explanation:
You want to know which of the given points satisfies the inequality.
GraphWe find it easiest to plot the given points on a graph of the solution. This shows us that (1, 2) is a solution to the inequality. (It lies in the solution area.)
__
Additional comment
Another way to choose the answer is to try each of the points in the inequality.
If you can visualize the boundary line (without plotting it) as a line with positive slope and a y-intercept of 2, you can more readily reject the first choice and accept the last choice. (0, 3) is above the y-intercept, and (1, 2) is to the right of it (in the solution space).
You may also recognize the x-intercept will be -3, so the second choice lies above the boundary line.

What is the position of B on the number line below?
Write your answer as a fraction or mixed number
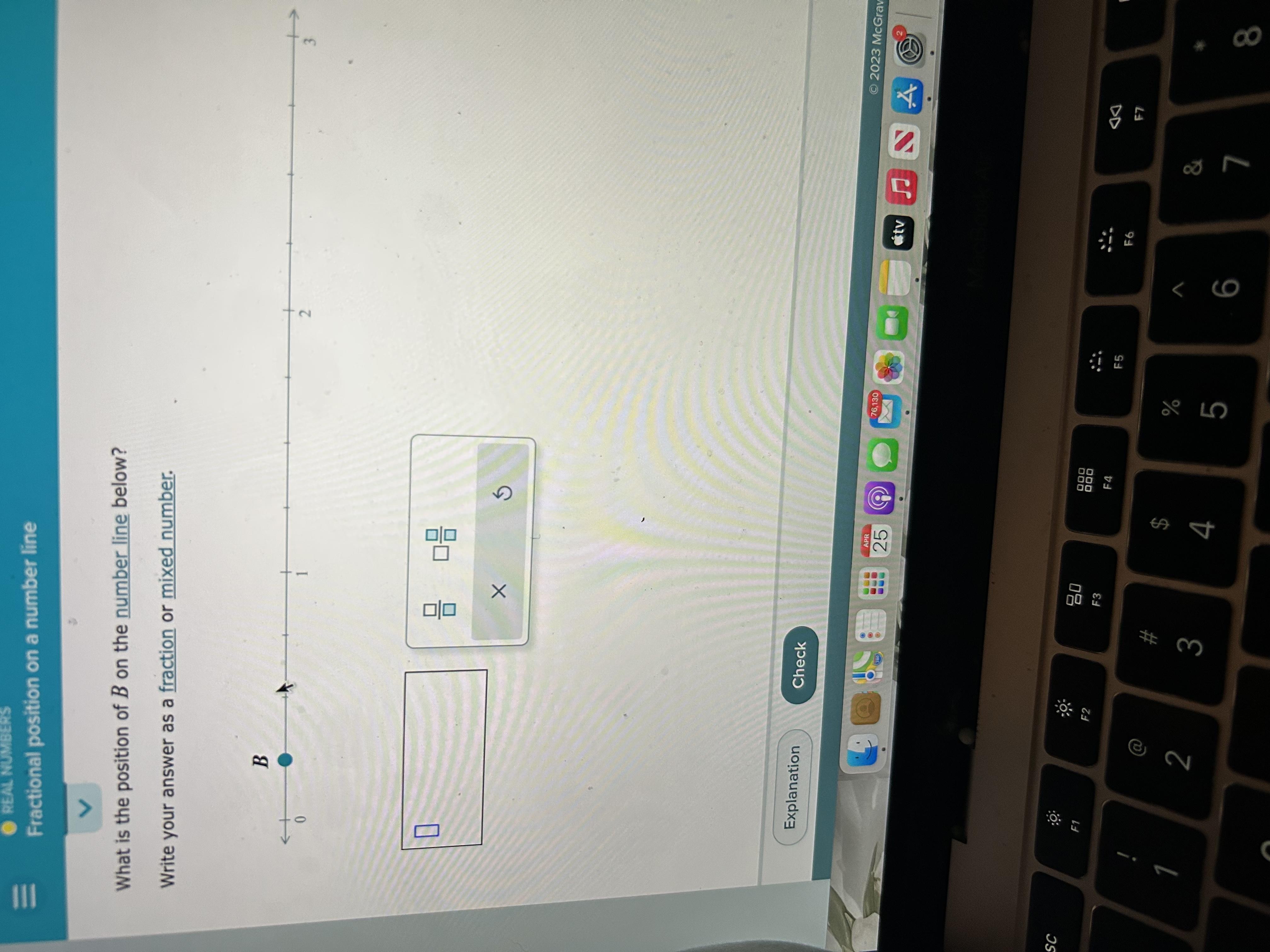
Answers
The requried position of point B on the number line is 1/4 or 0.25.
Since point B represents the number 0.25 on the number line, its position can be described as 0.25 units to the right of 0 or as 0.25 units to the left of 0.5.
Alternatively, we can describe its position as a fraction or mixed number using the length of the number line as the denominator. If the number line extends from 0 to 1, then the position of point B can be expressed as:
B = 0 + 0.25 = 1/4
Therefore, the position of point B on the number line is 1/4 or 0.25.
Learn more about number line here:
https://brainly.com/question/16191404
#SPJ1
What is negative 2 minus positive 4 equal?
Answers
Answer:
positive 2
Step-by-step explanation:
Negative 2 minus positive 4 equals negative 6.
What is negative 2 minus positive 4 equal?When you subtract two numbers, like negative 2 minus positive 4, you can think of it as adding the opposite number.
In this situation, when we subtract positive 4 from negative 2, we can express it as adding negative 4 to negative 2.
If you put together negative 2 and negative 4, you get negative 6.
Negative 2 take away positive 4 is the same as negative 6.
Learn more about negative numbers
https://brainly.com/question/20933205
#SPJ6
Find two numbers if their sum is -11 and their difference is 41
Answers
Answer:
The numbers are 12 and −29
Step-by-step explanation:
900 employees had put their names in a lucky draw. When the lucky numbers were drawn. The first draw eliminated 20% of the people, the second draw eliminated 30% of the remaining people and the third draw eliminated exactly one third of the remaining people. How many people were eliminated in the third draw?
Answers
Answer: in the third draw 33.33% people eliminated.
Step-by-step explanation:
A test has twenty questions worth 100 points. The test consists True/False questions worth 3 points each and multiple choice questions worth 11 points each. Howmany multiple choice questions are on the test?
Answers
Multiple choice questions = 5
True questions = 15
Given that:
Total number of questions = 20
Total worth of point = 100
Multiple choice questions (M) = 11 points each
True false questions (T) = 3 points each
Hence,
M + T= 20 ____(1)
11M + 3T = 100 ____(2)
M = 20 – T
Using the relation in (2)
11(20 – T) + 3T= 100
220 – 11T + 3T= 100
220 – 8T = 100
-8Tf = 100 – 220
-8T = – 120
T = 120/8
T = 15
Mc = 20 – 15
Mc = 5
Multiple choice questions = 5
True false questions = 15
Molly shared a spool of ribbon with 12 people. Each person received 3 feet of ribbon. Which equation can she use to find
r, the number of feet of ribbon that her spool originally had?

Answers
Answer: R/12=3
Step-by-step explanation: This is because / = divide so since we need to divide then multiply its better you go with /
Answer:D
Step-by-step explanation:
what is the solution to the equation:
5(n - 1/10) = 1/2
a. n= 13/5
b. n= 3/25
c. n= 0
d. n= 1/5
Answers
\( \sf \longrightarrow \: 5 \bigg( \: n - \frac{1}{10} \bigg) = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: 5 \bigg( \: \frac{n}{1} - \frac{1}{10} \bigg) = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: 5 \bigg( \: \frac{10 \times n - 1 \times 1}{1 \times 10} \bigg) = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: 5 \bigg( \: \frac{10n - 1}{ 10} \bigg) = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: \: \frac{50n - 5}{ 10} = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: \: 2(50n - 5) =1(10) \\ \)
\( \sf \longrightarrow \: \: 2(50n - 5) =10 \\ \)
\( \sf \longrightarrow \: \: 100n - 10=10 \\ \)
\( \sf \longrightarrow \: \: 100n =10 + 10\\ \)
\( \sf \longrightarrow \: \: 100n =20\\ \)
\( \sf \longrightarrow \: \:n = \frac{2 \cancel{0}}{10 \cancel{0}} \\ \)
\( \sf \longrightarrow \: \:n = \frac{1}{5} \\ \)
Answer:-
Answer:- D) n = ⅕ ✅To solve the equation \(\sf 5(n - \frac{1}{10}) = \frac{1}{2} \\\) for \(\sf n \\\), we can follow these steps:
Step 1: Distribute the 5 on the left side:
\(\sf 5n - \frac{1}{2} = \frac{1}{2} \\\)
Step 2: Add \(\sf \frac{1}{2} \\\) to both sides of the equation:
\(\sf 5n = \frac{1}{2} + \frac{1}{2} \\\)
\(\sf 5n = 1 \\\)
Step 3: Divide both sides of the equation by 5 to isolate \(\sf n \\\):
\(\sf \frac{5n}{5} = \frac{1}{5} \\\)
\(\sf n = \frac{1}{5} \\\)
Therefore, the solution to the equation \(\sf 5(n - \frac{1}{10})\ = \frac{1}{2} \\\) is \(\sf n = \frac{1}{5} \\\), which corresponds to option (d).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Which of the following is not one of Euclid’s postulates?
Answers
I think you forgot to list the following.
Given the equation of a line in standard form, determine the slope, y-intercept, and
sketch the line.
x-3y = -9
Answers
The slope of x - 3y = -9 is, m = 1/3, while the y-intercept (b) is 3.
The sketch of x - 3y = -9 is shown below.
How to Determine the Slope and Y-intercept of the Equation of a Line?To determine the slope and y-intercept of the line given by the equation x - 3y = -9, we can rewrite it in slope-intercept form y = mx + b, where m is the slope and b is the y-intercept.
To do this, we can solve for y:
x - 3y = -9
-3y = -x - 9
y = (1/3)x + 3
Now we can see that the slope of the line is m = 1/3, and the y-intercept is b = 3.
To sketch the line, we can use the slope and y-intercept. We can start by plotting the y-intercept (0,3) on the y-axis. From there, we can use the slope of 1/3 to find additional points on the line. For example, if we move 3 units to the right along the x-axis, we can move up 1 unit (since the slope is 1/3) to get another point on the line, which is (3,4). We can repeat this process to find more points on the line and then connect them to sketch the line.
The sketch is shown below in the attachment.
Learn more about the slope and y-intercept on:
https://brainly.com/question/10700419
#SPJ1
