00 Σ() 3)". =1 5n+ 1 (1 point) Consider the series Evaluate the the following limit. If it is infinite, 2n3 + 3 type "infinity" or "inf". If it does not exist, type "DNE". lim vanl = n-00 Answer: L = = What can you say about the series using the Root Test? Answer "Convergent", "Divergent", or "Inconclusive" Answer: Divergent Determine whether the series is absolutely convergent, conditionally convergent, or divergent. Answer "Absolutely Convergent", "Conditionally Convergent", or "Divergent". Answer: Divergent
Answers
The limit of the series is equal to infinity. Using the Root Test, we can see that the series is divergent. Therefore, the series is also divergent when considering absolute convergence.
Hi! To answer your question, let's break it down into its main parts.
1. Evaluate the limit:
lim (2n^3 + 3)/(5n^3 + 1) as n approaches infinity
Answer: As n approaches infinity, the dominant terms are 2n^3 and 5n^3. Therefore, the limit is 2/5.
2. Root Test:
The Root Test is inconclusive if the limit of the n-th root of the absolute value of the series' terms is equal to 1.
In this case, since the limit is 2/5 (not 1), the Root Test is inconclusive.
3. Determine the type of convergence:
The series is divergent because the limit is not equal to 0.
In conclusion, the limit of the given series is 2/5, the Root Test is inconclusive, and the series is divergent
Learn more about divergent series here: brainly.com/question/15415793
#SPJ11
Related Questions
Which of the following is most likely the next step in the series

Answers
Answer:
C.
Step-by-step explanation:
The pattern is the amount of sides each shape has.
Triangle - 3
Rectangle - 4
Pentagon - 5
Logically, the next shape would be a hexagon, a shape with 6 sides.
A rectangle has a length of 0.5 and a width of 0.25. Paulo needs to make a scale drawing of the rectangle with a scale factor of 12.
Match the length and width with the correct values for Paulo's scale drawing.
Answers
Answer: 6 inches and a width of 4 inches
Step-by-step explanation:
Answer:
The length is 6 and the width is 3
Step-by-step explanation:
Original length: 0.5
0.5 x 12 (scale factor) = 6
0.25 x 12 (scale factor) = 3
A 10 foot flagpole casts a 16 foot shadow how tall is 60 foot shadow
Answers
The height of the flagpole with a 60-foot shadow with maintaining the given ratio will be 37.5 feet.
What are the ratio and proportion?The ratio is the division of the two numbers.
For example, a/b, where a will be the numerator and b will be the denominator.
Proportion is the relation of a variable with another. It could be direct or inverse.
As per the given,
A 10-foot flagpole casts a 16 foot
The ratio of the flagpole's actual height to the length of the shadow
⇒ 10/16
Let's say the height of flagpoles whose shadow is 60 feet.
The ratio of the flagpole's actual height to the length of the shadow,
⇒ x/60
Both ratios must be the same.
Therefore, x/60 = 10/16
x = 600/16 = 37.5 foot.
Hence "The height of the flagpole with a 60-foot shadow with maintaining the given ratio will be 37.5 feet".
For more information about ratios and proportions,
brainly.com/question/26974513
#SPJ1
if the expected frequencies rule for chi-square had been violated by the data, which categories could be combined together in a meaningful way to increase the expected frequencies?
Answers
If the chi-square test's expected frequencies rule is broken, either the row or the column is combined to provide a higher frequency that can be used to run the independence test.
Generally speaking, if more than 20% of the anticipated frequencies have a value of less than 5, Chi-Square should not be used (it does not matter what the observed frequencies are).
Both the chi-square test and Fisher's exact test are inappropriate if the sampled values' independence is broken. This presumption will be broken if the same subject results in more than one observation in the contingency table.
There are distinct assumptions for each non-parametric test as well. The data in the cells should represent frequencies or counts of cases rather than percentages or other data transformations, according to the Chi-presumptions. square's The variables' levels are mutually exclusive.
To know more about chi-square refer to the given link:
https://brainly.com/question/14082240?referrer=searchResults
#SPJ4
Is AABC-AXYZ? If so, identify the similarity postulate or theorem that
applies
30°
30"
45
15
959
c.
959
А
A. Similar - SSS
B. Similar - AA
C. Similar - SAS
D. Cannot be determined

Answers
The theorem that applies to the similar triangles is AA theorem.
How to find similar triangles?Similar triangles are triangle with same shapes but may be different sizes.
Similar triangle have corresponding sides as a ratio of each other.
The triangles above have two of their angles equal, therefore, the triangles are similar.
They are similar by AA theorem.
AA theorem of similarity states that If two of angles are equal, then the third angle must also be equal, because angles of a triangle always add to make 180°.
30 ≅ 30
95 ≅ 95
learn more on similar triangles here: https://brainly.com/question/16999173
#SPJ1
Let R be a commutative ring with identity and let I₁,..., In be R-ideals with I; +Ij = R whenever i + j. Show that I₁ ...In = I1 · ... · In·
Answers
To prove that I₁ ...In = I₁ · ... · In, we need to show that both sets contain the same elements.
First, we will show that I₁ ...In ⊆ I₁ · ... · In. Let x ∈ I₁ ...In. This means that x can be written as a product of elements, where each element is in one of the ideals I₁,...,In. Since I₁,...,In are R-ideals, this product is also in each of the ideals I₁,...,In. Therefore, x ∈ I₁ · ... · In.
Next, we will show that I₁ · ... · In⊆ I₁ ...In. Let x ∈ I₁ · ... · In. Then x can be written as a product of elements, where each element is in one of the ideals I₁,...,In. By assumption, each ideal I_i has a complement in the form of another ideal J_i such that I_i + J_i = R. Since the product of elements in I_i can be multiplied with elements in J_j without restriction, we can replace each element in the product with an element in its complement. Specifically, let x_i ∈ I_i and y_i ∈ J_i such that x = x₁y₁...x_ny_n. Then each x_i ∈ I_i and y_i ∈ J_i, and since I_i + J_i = R for all i, we can write 1 as a sum of products of elements in the complements J_i. Specifically, 1 = ∑j_1∈J₁...∑j_n∈J_n p(j₁, ... , j_n) where p(j₁, ... , j_n) is a product of elements of the form y_i or y_i y_j where j ≠ i. Multiplying x by this expression, we get:
x = x(∑j_1∈J₁...∑j_n∈J_n p(j₁, ... , j_n)) = ∑j_1∈J₁...∑j_n∈J_n (x₁j₁...x_nj_n)y₁...y_n
Each term in this sum is in I₁...In since each term contains an element from I_i and an element from J_i for each i. Therefore, x ∈ I₁...In.
Combining the two inclusions, we have shown that I₁...In = I₁ · ... · In.
Learn more about ideals here:
https://brainly.com/question/12961537
#SPJ11
Let T(x,y)=(−1x+y+z,−1x−3y+2z,z)T(x,y)=(-1x+y+z,-1x-3y+2z,z). 1. Find the image of (2,−1,−3)(2,-1,-3) 2. Find the preimage of (−1,5,2)(-1,5,2).
Answers
The image of the given point (2, -1, -3) is (-4, 1, -3). and , the required pre-image of the given point (-1, 5, 2) is (1, 2).
Let T(x,y) = (-x + y + z, -x - 3y + 2z, z)
Here is the solution to the given problem.
Image of the given point (2, -1, -3):T(2, -1, -3) = (-2 + 1 - 3, -2 - 3 + 6, -3)= (-4, 1, -3)
Therefore, the image of the given point (2, -1, -3) is (-4, 1, -3).
Pre-image of the given point (-1, 5, 2):
We have T(x,y) = (-x + y + z, -x - 3y + 2z, z)
Now, we can equate T(x,y) = (-1, 5, 2)as (-x + y + z, -x - 3y + 2z, z) = (-1, 5, 2)
Comparing the first element, we have,-x + y + z = -1y = x + z - 1
Comparing the second element, we have,-x - 3y + 2z = 5-x - 3(x + z - 1) + 2z = 5-4x - z = 8z = 4x - 3
Now, comparing the third element, we have z = 2
We get z = 2 from the third element above.So, x = 1, from the first element
y = 2 from the relation obtained earlier
Therefore, pre-image of the given point (-1, 5, 2) is (1, 2).
Learn more about equation at
https://brainly.com/question/29016558
#SPJ11
Please help I need this answer asap
a
b
c
d

Answers
Answer:
Step-by-step explanation:
b
I need help finding location of j

Answers
Answer:
\(-15\)
Step-by-step explanation:
\(11-(-2)\\11+2\\13\)
Line KL has a range of 13.
Line JK has the same range covered as line KL.
\(-2-13\)
\(-15\)
J is located at -15.
A town has a population of 19000 and grows at 4.5% every year. To the nearest tenth
of a year, how long will it be until the population will reach 49000?
Answers
Answer:
33.1 years
Step-by-step explanation:
Let x be the number of years it takes for the population to reach 49000.
Starting with a population of 19000 and growing at 4.5% per year, the population after t years can be represented by the exponential function:
P(x) = 19000(1 + 0.045)^x
We want to find the value of x that makes P(x) = 49000.
=> 49000 = 19000(1 + 0.045)^x
Dividing both sides by 19000, we get:
=> 2.57895 = 1.045^x
Taking the logarithm of both sides with base 10, we get:
=> log(2.57895) = x log(1.045)
=> x = log(2.57895) / log(1.045)
=> x ≈ 33.1
Therefore, it will take approximately 33.1 years for the population to reach 49000.
Answer: 21.5 cause i got the answer wrong and they gave me the correct answer
uppose that a particular nba player makes of his free throws. assume that late in a basketball game, this player is fouled and is awarded two free throws. a. what is the probability that he will make both free throws? (to 4 decimals) b. what is the probability that he will make at least one free throw? (to 4 decimals)
Answers
Answer:
a. 0.81
b. 0.81
Step-by-step explanation:
Let's assume that the player makes x% of his free throws. Then, the probability that he will make both free throws is (x/100)^2, and he will make at least one free throw is 1 - (1 - x/100)^2.
So if he makes 90% of his free throws, then:
a. The probability that he will make both free throws is (90/100)^2 = 0.81.
b. The probability that he will make at least one free throw is 1 - (1 - 90/100)^2 = 1 - (1 - 0.9)^2 = 1 - 0.19 = 0.81.
The answers to the questions rounded to 4 decimal places are:
a. 0.81
b. 0.81
Each batch of cookies uses 0.75 cups of sugar. How many cups of sugar are used in 4.5 batches of cookies?
A) 3.375
B) 3.75
C) 4.375
D) 4.75
Answers
Answer:
A)3.375
Step-by-step explanation:
0.75 * 4.5 = 3.375
Answer: A)3.375
Few years late
Raul bought 6 tangerines and ate 2/3 of them. Omar bought 8 tangerines and ate 1/4 of them. Who ate more tangerines?
Answers
Rahul ate more tangerines...
can someone please solve this? I clicked on homework help and it wasn't much help. I'm trying to turn in as much missing assignments as I can before school ends on Thursday. Thank you!

Answers
Answer:
One proportion to solve is 8/18 = x/8Exact answer as a fraction: x = 32/9Approximate answer in decimal form: x = 3.556In reality, the 5's go on forever, but we have to round off somewhere.
========================================================
Explanation:
Break up the triangles as your teacher recommends. See the diagram below as to what I mean.
The smaller triangle has A = 8 as the horizontal side, and B = x as the vertical side
The larger triangle has C = 10+8 = 18 as the horizontal aside, and D = 8 as the vertical side.
We can form the proportion A/C = B/D.
A/C connects the horizontal sides (small/large) while B/D has the vertical sides tied together. The order of division is the same small over large. You could do large over small, but make sure you keep both sides consistent.
-----------------
Let's solve for x
A/C = B/D
8/18 = x/8
8*8 = 18*x .... cross multiply
64 = 18x
18x = 64
x = 64/18 .... divide both sides by 18
x = 32/9 exactly in fraction form
x = 3.556 approximately in decimal form
-------------------
Another proportion you can solve is A/B = C/D and you should get the same x value. It's the same as A/C = B/D because the B and C swap places. There are many other approaches you could take using different proportions.

NEED HELP ASAP!!!!!
What is the probability that both events will occur?
A coin and a die are tossed.
Event A: The coin lands on heads
Event B: The die is 5 or greater
P(A and B)= ?

Answers
The probability that both Event A (coin lands on heads) and Event B (die is 5 or greater) will occur is 1/6.
To find the probability that both Event A (coin lands on heads) and Event B (die is 5 or greater) will occur, we need to determine the individual probabilities of each event and then multiply them together since the events are independent.
Event A: The coin lands on heads
A fair coin has two equally likely outcomes, heads or tails. Since we are interested in the probability of heads, there is only one favorable outcome out of two possible outcomes.
P(A) = 1/2
Event B: The die is 5 or greater
A fair six-sided die has six equally likely outcomes, numbers 1 through 6. Out of these six outcomes, there are two favorable outcomes (5 and 6) for Event B.
P(B) = 2/6 = 1/3
To find the probability of both events occurring (A and B), we multiply the individual probabilities:
P(A and B) = P(A) * P(B) = (1/2) * (1/3) = 1/6
Therefore, the probability that both Event A (coin lands on heads) and Event B (die is 5 or greater) will occur is 1/6.
For more question on probability visit:
https://brainly.com/question/24756209
#SPJ8
The vertices of △JKL are J(−3, −2), K(1, 4), and L(4, 2). Find the vertices of the image of △JKL under the dilation centered at the origin with scale factor 5.
Answers
The coordinate pairs of vertices D₅ (△JKL) of are J'(-15,-10), K'(5,20) and L'(20,10).
What does a math definition of a coordinate plane mean?
A surface with two dimensions known as the coordinate plane is created by two number lines. The x-axis is a single number line that runs horizontally. The y-axis is the name given to the vertical number line that is the other number line.
A place known as the origin is where the two axes collide. To graph points, lines, and other things, we can utilize the coordinate plane.
We know that, D₅ (△JKL) means triangle JKL dilated by scale factor 5 with origin as center of dilation.
If a figure is dilated by factor k and origin is the center of dilation, then
( x, y ) ⇒ ( kx , ky )
From the given problem, the rule of dilation is
( x , y ) ⇒ ( 5x , 5y )
Now
J( -3 , -2 ) ⇒ J'( 5(-3), 5(-2)) = J'( -15 , -10 )
K( 1,4 ) ⇒ K'(5(1) , 5(4)) = K'( 5,20 )
L( 4,2 ) ⇒ L'(5(4), 5(2)) = L'( 20,10 )
Therefore, the coordinate pairs of vertices D₅ (△JKL) of are J'(-15,-10), K'(5,20) and L'(20,10).
Learn more about a coordinate plane
brainly.com/question/21829586
#SPJ1
The volume of a cone-shaped hole is 21πft3 If the hole is 7ft deep, what is the radius of the hole?
Answers
Answer:
r = 3ft
Step-by-step explanation:
example of a cone-shaped hole is a funnel
V = 1/3 • π • r² • height
21π = 1/3 • π • r²• height
(21)3 = (1/3 • r² • 7)3
63/7 = (r² • 7)/7
√9 = √r²
r = 3
How do I find the vertex and the standard form? Plz explain
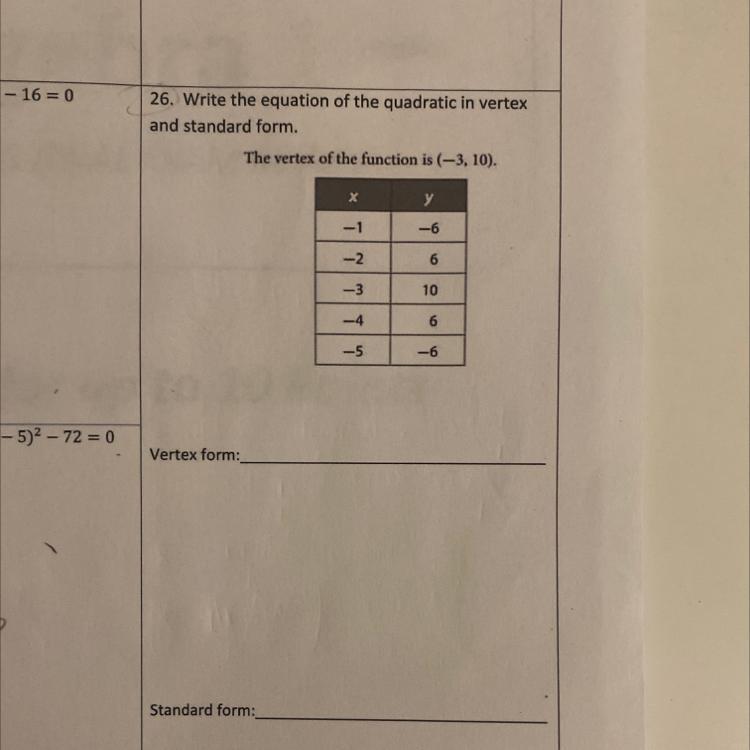
Answers
Answer:
Vertex form
y = -4(x + 3)^2 + 10
Standard form;
y = -4x^2-24x - 26
Step-by-step explanation:
Mathematically, we have the vertex form as
y = a(x-h)^2 + k
(h,k) represents the vertex
We have h as -3 and k as 10
y = a(x+3)^2 + 10
To get a, we substitute any of the points
Let us use (-1,-6)
-6 = a(-1+3)^2 + 10
-6-10 = 4a
4a = -16
a = -16/4
a = -4
So we have the equation as;
y = -4(x+3)^2 + 10
For the standard form;
We expand the vertex form;
y = -4(x + 3)(x + 3) + 10
y = -4(x^2 + 6x + 9) + 10
y = -4x^2 - 24x -36 + 10
y = -4x^2 -24x -26
Which equation represents a line that is parallel to the line represented by
4x + y = 7 and passes through the point (1, 8)?
Answers
Answer:
y = -4x + 12
Step-by-step explanation:
For a line to be parallel, it needs to have the same slope.
Point intercept form: y - y₁ = m (x - x₁)
Where y and x are just kept as y and x, y₁ and x₁ are the parts of a coordinate, and m = slope.
So, in order for the line to be parallel, it needs to have the same slope as the first equation. The slope of the line (which is the "m" in y = mx + b) is..
4x + y = 7
y = -4x + 7
So, m, or the slope, is -4.
Plug this, along with the coordinate the problem gives you into point-intercept form.
y - y₁ = m (x - x₁)
y - 8 = -4 (x - 1)
Simplify.
y - 8 = -4x + 4
Add 8 to both sides.
y = -4x + 12
The formula 2y = 3x + 6 is used in chemistry. How can this formula be solved for Y?
Answers
\(2y = 3x + 6\\y = \frac{3}{2}x + \frac{6}{2} = \frac{3}{2}x + 3\)
Carmela made $270 working at a pet store last week. she worked a total of 30 hours. How much money did carmela make per hour?
Answers
Answer:
Carmela made $9 per hour
270÷30=9
Hope this helps !
Math is the only place where is not questionable as to why someone has 83.
Answers
Answer:
true
Step-by-step explanation:
help me please, i have no idea what im supposed to be doing and my teacher isnt much help so im hoping someone else can help me

Answers
Answer:
(4, 2 ) and (2, 4 )
Step-by-step explanation:
xy = 8 → (1)
y = - x + 6 → (2)
substitute y = - x + 6 into (1)
x(- x + 6) = 8
- x² + 6x = 8 ( subtract 8 from both sides )
- x² + 6x - 8 = 0 ( multiply through by - 1 )
x² - 6x + 8 = 0 ← in standard form
(x - 4)(x - 2) = 0 ← in factored form
equate each factor to zero and solve for x
x - 4 = 0 ⇒ x = 4
x - 2 = 0 ⇒ x = 2
substitute these values into (2) for corresponding values of y
x = 4 : y = - 4 + 6 = 2 ⇒ (4, 2 )
x = 2 : y = - 2 + 6 = 4 ⇒ (2, 4 )
2 1. Determine the missing length in the following triangle. Round to the nearest tenth. (2 points: 1 point for correct answer, 1 point for showing your work) 20 Xe 16 Your answer

Answers
Here, we have a right triangle with a missing side length.
To determine the length of the missing side, apply pythagorean theorem
\(c^2=a^2+b^2\)Where:
c is the longest side (hypotenuse) = 20
a = 16
Substitute values into the equation and solve for the missing side.
We have:
\(\begin{gathered} 20^2=16^2+x^2 \\ \\ 400=256+x^2 \end{gathered}\)Subtract 256 from both sides:
\(\begin{gathered} 400-256=256-256+x^2 \\ \\ 144=x^2 \end{gathered}\)Take the square root of both sides:
\(\begin{gathered} \sqrt[]{144}=\sqrt[]{x^2} \\ \\ 12=x \\ \\ x=12 \end{gathered}\)Therefore, the missing length is 12 units
ANSWER:
x = 12
the sum of x and 10 is less than -6
Answers
Twice: 2 times
The sum of: add
A number: choose a variable, like x
---Thus "the sum of a number and 4" becomes "add x and 4" which, mathematically, is "x+4"
-----Continuing to put it all together, "Twice the sum of a number and four" becomes "2 times (x+4)" which, mathematically, is "2(x+4)"
Is: equals
-------"Twice the sum of a number and four is" becomes "2(x+4)="
23 less than: subtract 23. This one tends to trick people; "23 less than" will become "__ - 23", NOT "23 - __"
three times the number: 3 times x
---"23 less than three times the number" becomes "subtract 23 from 3 times x" which, mathematically, is "3x-23"
-------So the final phrase: 2(x+4)=3x-23"
convert 7/9 in a long division
Answers
Step-by-step explanation:
The answer is in the picture above

1. given the bilateral z- transform: ???????? (z) = z 2 (z 2−1/4) a) (3 points) find the partial fraction expansion: ???????? (z) = K1 z z−???? + K2 z z−???? show work.
Answers
The partial fraction expansion of the given bilateral z-transform expression is to be found. It can be expressed as ???????? (z) = K1 z / (z - ???? ) + K2 z / (z - ???? ). The steps to determine the values of K1 and K2 will be explained.
To find the partial fraction expansion of the given expression, we first factorize the denominator as (z - ???? )(z - ???? ), where ???? and ???? are the roots of the denominator. In this case, the roots are 1/2 and -1/2.
Next, we express the expression as a sum of two fractions, with each fraction having a distinct root in the denominator. The partial fraction expansion can be written as:
???????? (z) = K1 z / (z - 1/2) + K2 z / (z + 1/2)
To determine the values of K1 and K2, we can multiply both sides of the equation by the common denominator (z - 1/2)(z + 1/2) and equate the numerators. This gives us:
z 2 (z 2 - 1/4) = K1 z(z + 1/2) + K2 z(z - 1/2)
Expanding and collecting like terms, we get:
z 2 (z 2 - 1/4) = (K1 + K2)z 2 + (K1/2 - K2/2)z
By comparing the coefficients of like powers of z on both sides, we can determine the values of K1 and K2. Equating the coefficients, we have:
K1 + K2 = 1
K1/2 - K2/2 = -1/4
Solving these equations simultaneously, we can find the values of K1 and K2, which will complete the partial fraction expansion.
Learn more about coefficients here:
https://brainly.com/question/13431100
#SPJ11
What is the image point of (5,1)(5,1) after a translation right 5 units and down 2 units? PLS HELP ME
Answers
Answer:
the answer would be(0, -1) happy to help you ahmed
Step-by-step explanation:

Answer:
-1
Step-by-step explanation:
hope this helps
Find the length of the missing side

Answers
Answer:
43.7378554573
Step-by-step explanation:
use pythagoream thereom :D
In circle S with \text{m} \angle RUT= 30m∠RUT=30, find the \text{m} \angle RSTm∠RST.

Answers
Answer:
m∠RST= m RT= 60°
⭒⭒⭒⭒⭒⭒⭒⭒⭒⭒⭒⭒
m RT=2 m∠ROT= 2 (30)=60°✎--------------
hope it helps...
have a great day!!